Треугольники с фиксированными углами
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
треугольника
в котором
Точка
на стороне
такова, что
Точка
— середина отрезка
Докажите, что
Отметим на точку
такую, что
![]()
Тогда прямоугольный треугольник. Значит, перпендикуляр из
на
падает в середину по теореме Фалеса, следовательно,
лежит на серединном перпендикуляре
А так как
то
лежит и на серединном перпендикуляре
Ошибка.
Попробуйте повторить позже
Точки и
— середины сторон
и
параллелограмма
Из его вершины
на прямую
опустили перпендикуляр
На стороне
выбрали точку
так, что углы
и
равны. Найдите
Подсказка 1
Интересно, что нам дает условие про равные углы? На картинке они расположены неудобно. Вот бы придумать доп. построение, чтобы равные углы оказались в одном треугольнике(и тогда он равнобедренный)/равных треугольниках.
Подсказка 2
Давайте продлим KE до пересечения с BC! Тогда возникнет равнобедренный треугольник HFG (где G - точка пересечения BC и EK). А еще возникают равные треугольники EDK и KCG! С этим уже приятнее работать. Подумайте, как теперь применить условие, что BHK - прямой угол (посчитайте уголки на чертеже)
Подсказка 3
Можно доказать, что BHF тоже равнобедренный! Какая приятная картинка - так много равных сторон. Давайте обозначать их за переменные. Например, ED = a, FC = b (или как-то по-другому на ваше усмотрение). Осталось выразить BF:FC, используя факты из прошлых подсказок
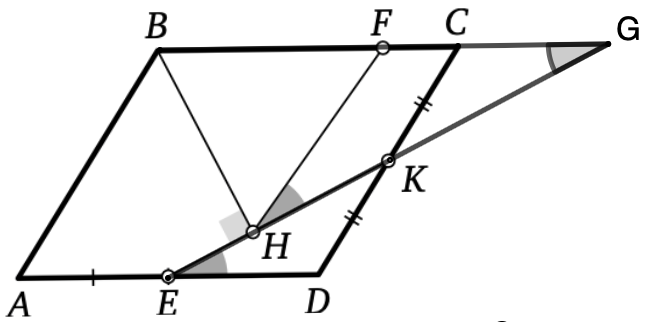
Продлим за точку
пересечем с прямой
получим точку
как накрест лежащие при параллельных
прямых
и
и секущей
а значит, треугольник
равнобедренный и
Аналогично треугольник
равнобедренный с углом при основании
то есть
Отсюда
Рассмотрим
треугольники
и
Они равны по стороне и двум прилежащим к ней углам
как
накрест лежащие углы при параллельных прямых). Значит,
пусть
тогда
отсюда
Ошибка.
Попробуйте повторить позже
Два треугольника пересекаются по шестиугольнику , в котором
Найдите углы этих треугольников.
Источники:
Подсказка 1
Обратите внимание, что есть два случая для пересечения треугольников.
Случай (стороны треугольника - тройки несмежных сторон):
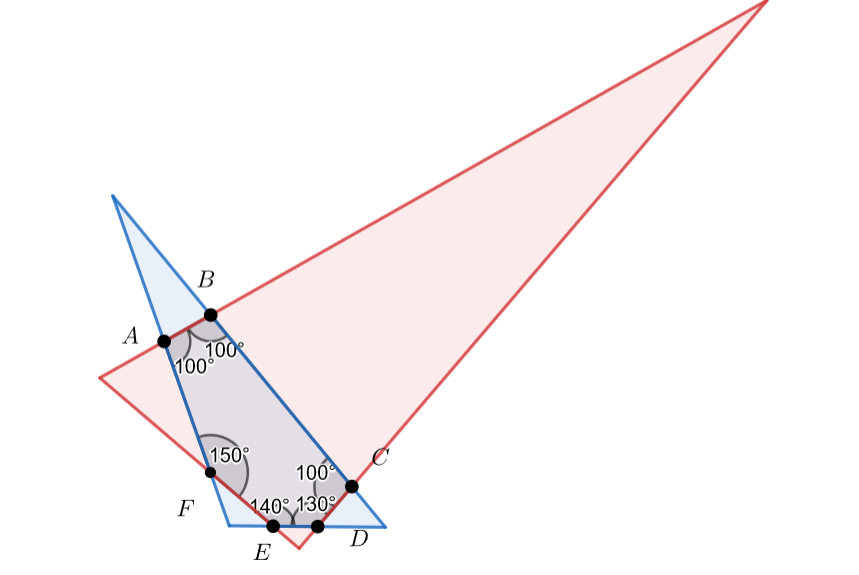
В таком случае все углы треугольников легко находятся, как , где
- два соседних угла
шестиугольника.
Тогда получаем, что углы красного треугольника равны , а углы синего -
.
Случай (один из углов шестиугольника совпадает с углом треугольника):
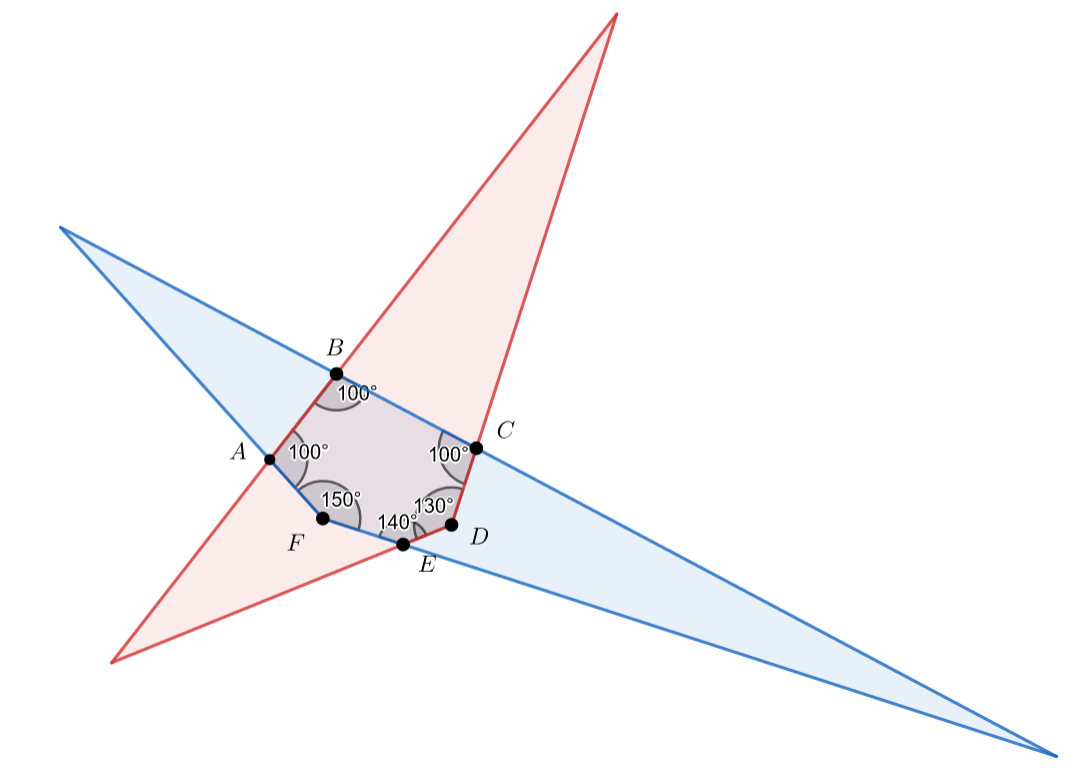
Заметим, что это единственное возможное положение в этом случае. Углы синего треугольника равны ;
и
.
Углы красного треугольника будут равны
и
.
и
; или
и
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике с прямым углом
проведена высота
Пусть
и
центры вписанных окружностей
треугольников
и
соответственно. Докажите, что
перпендикулярно

Заметим, что
А значит, откуда
Аналогично
откуда следует, что
это ортоцентр треугольника
А значит
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике гипотенуза
равна
Пусть
— высота этого треугольника,
— высота
треугольнике
Найдите длину
Подсказка 1
Начнем разбираться с условием) KH - катет напротив угла в 30 градусов в прямоугольном треугольнике KAH, тогда он равен половине гипотенузы AH! Осталось найти AH. Для этого свойство про 30 градусов возможно придется применить снова
Подсказка 2
Обратим внимание, что треугольник HBC тоже прямоугольный с углом 30 градусов. Как теперь посчитать AH?
Заметим, что Тогда в прямоугольном треугольнике
угол
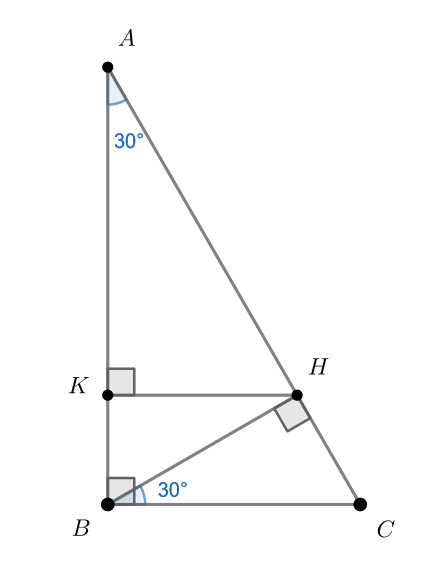
В прямоугольном треугольнике катет напротив угла в равен половине гипотенузы. То есть для прямоугольных треугольников
выполнено:
Откуда Тогда
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике угол
равен
Точка
— середина стороны
Точка
симметрична точке
относительно стороны
Отрезки
и
пересекаются в точке
Прямые
и
пересекаются в точке
Докажите,
что
Подсказка 1
Что хорошего можно сказать про отражение M относительно BC? У нас ведь понятные углы на картинке.
Подсказка 2
Получаем, что треугольник MBP - равносторонний. На картинке есть ещё один отрезок, по длине равный стороне MBP. Хотелось бы полезный вывод из равенств отрезков.
Подсказка 3
Ага, треугольник APB является прямоугольным, ещё и с углами 30, 60. Может у нас где-то ещё есть треугольник с такими углами?
Подсказка 4
Действительно, треугольник AQB равнобедренный, QM - его высота, вот уже угол 90 градусов. Не забываем, что хотим приблизиться к отрезку MR, так что из имеющихся прямоугольных треугольников нас интересует ARM. Осталось посчитать остальные его углы и доказать равенство треугольника с APB.
Проведем . Заметим, что
при этом
тогда треугольник
— правильный. Тогда
Следовательно, треугольник
— прямоугольный. Мы знаем, что
Тогда треугольник
— равнобедренный с
основанием
Получаем, что
— высота в этом треугольнике, следовательно, треугольник
— прямоугольный с
углом
равным
и
То есть треугольники
и
равны. Тогда
что и
требовалось.
![]()
Ошибка.
Попробуйте повторить позже
Один из углов треугольника равен . Докажите, что треугольник, образованный основаниями биссектрис данного, —
прямоугольный.
Биссектриса — это ГМТ точек, равноудалённых от сторон угла. Заметим, что лежит на биссектрисе
. Опустим перпендикуляры
и
на
и
соответственно. Тогда, так как
лежит на биссектрисе
.
Так как , а
— биссектриса
Тогда опустим перпендикуляр
на
![]()
Так как — биссектриса угла
а
(доказано выше). Значит,
Получается,
—
биссектрисса
. Аналогично доказываем, что
— биссектрисса
Тогда:
Значит, в угол
.
— прямоугольный.
Ошибка.
Попробуйте повторить позже
Точки и
лежат на сторонах соответственно
и
ромба
причём
Известно, что треугольник
— равносторонний. Найдите угол
Подсказка 1
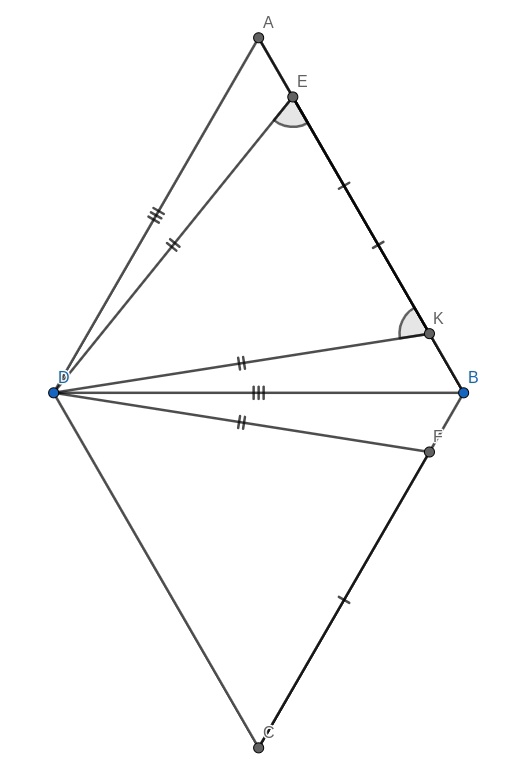
Отметьте точку K на стороне AB такую, что AK = BE. Теперь попробуйте найти равные треугольники с общей вершиной в точке D.
Подсказка 2
Попробуйте теперь доказать, что углы AKD и BED равны, и найти с ними пару равных треугольников.
Подсказка 3
Из равенства треугольников AKD и BED следует равенство отрезков AD и BD. Осталось вспомнить, что ABCD является ромбом.
На стороне отложим отрезок
Из равенства треугольников
и
(по двум сторонам и углу между ними)
следует, что
Углы при основании
равнобедренного треугольника
равны, поэтому равны и смежные им углы
и
и треугольники
и
равны по двум сторонам и углу между ними. Значит,
то есть
треугольник
равносторонний. Следовательно,
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике катет
а гипотенуза
Найдите длину биссектрисы
Подсказка 1
Пусть L делит сторону AC на отрезки длиной AL= x и CL = y. Попробуйте выразить x через y, используя основное свойство биссектрисы.
Подсказка 2
Получиться, что y = x*18/7. Теперь чему равна сторона AC (через x)?
Подсказка 3.
Верно! AC = 25/7*x. Осталось воспользоваться теоремой Пифагора и решить уравнение на x.
Пусть делит сторону
на отрезки длиной
и
![]()
По свойству биссектрисы Тогда
По теореме Пифагора
Остается найти
По теореме Пифагора то есть
Решаем это уравнение и получаем Итак,
- 8,4
- 8.4
Ошибка.
Попробуйте повторить позже
В треугольнике медиана, проведённая из вершины
в четыре раза меньше стороны
и образует с этой стороной угол
Найдите угол
Обозначим медиану из вершины через
Первое решение.
Опустим перпендикуляр на прямую
Тогда в прямоугольном треугольнике
катет
равен половине гипотенузы
так как лежит напротив угла в
градусов. А ещё по условию
Тогда
Получили, что в четырёхугольнике
диагонали точкой пересечения
делятся пополам, а значит, это параллелограмм, так что
В итоге
![]()
Второе решение.
Отметим ещё середину — как
а середину
— как
Тогда
а ещё по условию
Так что
треугольник
— равносторонний (
) с углом при вершине
в
значит, он равносторонний.
Тогда как смежный с углом в
Далее,
поэтому треугольник
— прямоугольный, и
Смежный с ним
С другой стороны, этот же угол равен
так как
— средняя линия
треугольника
— параллельна
![]()
Третье решение.
Не будем думать и просто посчитаем:
1) по теореме косинусов для треугольника
2) по формуле медианы (при удвоение медианы получается параллелограмм, у которого сумма квадратов диагоналей равна сумме квадратов всех сторон)
3) по теореме косинусов для треугольника
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике точка
— середина гипотенузы
На катетах
и
отмечены точки
и
соответственно так, что
Докажите, что
Подсказка 1
Нужное равенство похоже на теорему Пифагора, поэтому попробуем ее применить. У нас есть прямой угол ∠ACB. Как можно перебросить куда-нибудь BQ так, чтобы получился новый прямой угол?
Подсказка 2
Верно! Удвоив MQ за точку M к новой точке T, получим параллелограмм ATBQ. Тогда угол ∠CAT прямой и BQ = AT. Что теперь осталось доказать?
Подсказка 3
Точно! Остается проверить, что PT = PQ. Вспомним, что ∠PMQ тоже прямой. Как тогда доказать нужное равенство?
.png)
Чтобы доказать это равенство, соберём все отрезки в один прямоугольный треугольник и применим теорему Пифагора.
Удвоим до точки
за точку
Заметим, что
является параллелограммом, поскольку его диагонали пересекаются в
своих серединах. Отсюда
и
Остаётся доказать, что (и из треугольника
мы получим требуемое). Но действительно,
является медианой (по
построению) и высотой (по условию) треугольника
откуда он равнобедренный и
Ошибка.
Попробуйте повторить позже
и
— высоты остроугольного треугольника
в котором
Точки
и
— соответственно центр
описанной окружности и ортоцентр треугольника
Докажите, что прямая
проходит через середину отрезка
Подсказка 1
Угол в 45 градусов…Где же он встречается…Ого, а что насчет треугольников BA1A и BC1C? Что про них можно сказать? А что это дает?
Подсказка 2
Верно, они прямоугольные и равнобедренные, но тогда высоты в этих треугольниках - это серединные перпендикуляры. А значит пресечения высот в этих треугольниках - центр описанной окружности треугольника ABC. Нам нужно доказать, что в четырехугольнике C1OA1H точкой пересечения диагоналей, диагональ OH делится пополам. А где еще мы что-то очень похожее слышали? Что можно сказать про этот четырехугольник?
Подсказка 3
Поскольку данный четырехугольник образован серединными перпендикулярами и высотами в одном треугольнике, то данный четырехугольник является параллелограммом. А что мы знаем насчет диагоналей параллелограмма?
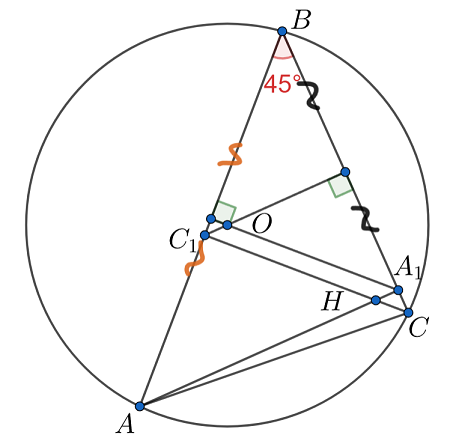
По условию а значит,
и
— равнобедренные. Отсюда
лежит на серединном перпендикуляре к
а
— на серединном перпендикуляре к
Также на обоих перпендикулярах находится точка
Но тогда
откуда
Аналогично
откуда
— параллелограмм, а значит
делится
пополам.
Ошибка.
Попробуйте повторить позже
Равносторонние треугольники и
расположены так, что вершина
лежит на стороне
, а вершина
— на стороне
.
Докажите, что
.
Подсказка 1
Хм, здесь есть много равных углов. Это намекает на то, что стоит поискать вписанные четырёхугольники!
Подсказка 2
Конечно, тут есть два вписанных четырёхугольника, имеющих общую сторону CR. Как же воспользоваться их вписанностью?
Подсказка 3
Верно, используем факт, что противоположные углы в сумме дают 180 градусов, надо просто перекинуть уголки, чтобы получить нужную сумму односторонних углов для искомых прямых!
Проведем рассмотрим четырехугольники
и
.
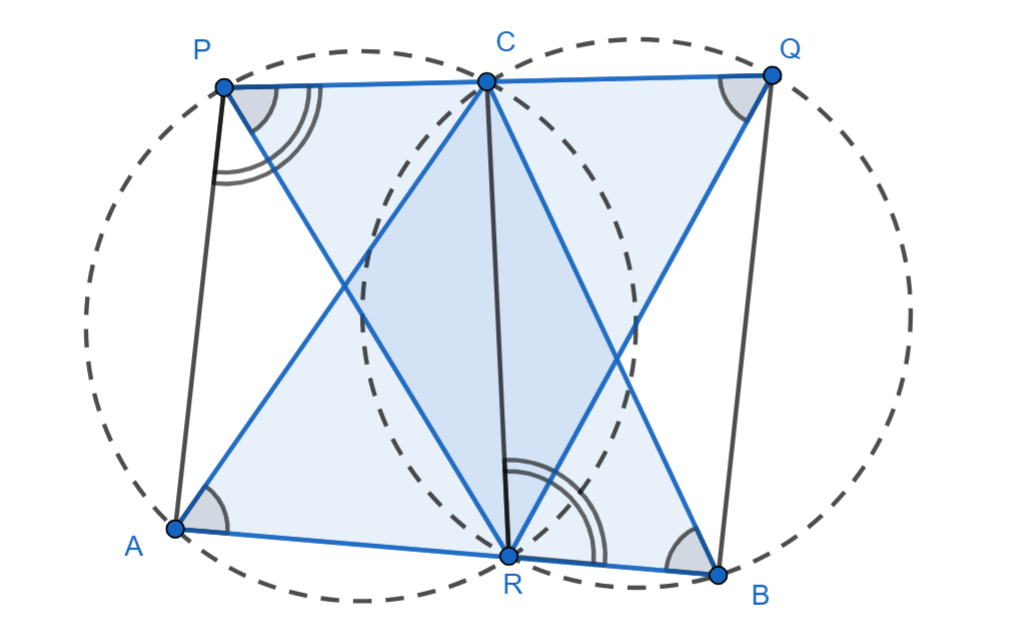
Поэтому
Следовательно,
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Неравнобедренный треугольник в котором
вписан в окружность
На биссектрисе угла
выбрана точка
а на биссектрисе угла
— точка
так, что
и
Прямая
пересекает
в точках
и
Докажите,
что треугольник
равнобедренный.
Так как то
Аналогично
Обозначим
Пусть
Обозначим
через
середину дуги
окружности
Тогда треугольник
равносторонний(
). Поэтому точка
—
центр описанной окружности треугольника
Следовательно:
Аналогично откуда
Итак, точка лежит на прямой
будем считать, что она совпадает с
Пусть
— середина меньшей дуги
окружности
Заметим, что
Значит, точка также лежит на прямой
и треугольник
совпадает с треугольником
Этот треугольник
равнобедренный, поскольку
![]()
Ошибка.
Попробуйте повторить позже
Дан пятиугольник в котором
,
Найдите величину угла
(в градусах).
Заметим, что треугольники и
равны, так как
и
Следовательно,
то есть
треугольник
равнобедренный. Пусть
и
тогда
и
но
поэтому
А из треугольника
получаем
Значит, Треугольник
равнобедренный, поэтому
В итоге
Ошибка.
Попробуйте повторить позже
В треугольнике с углом
сторона
больше стороны
Точка
на отрезке
такова, что
а
точка
на прямой
такова, что
Найдите величину угла
(в градусах).
Поскольку то сторона
— средняя по величине: по условию
значит
Поскольку сумма углов в
треугольнике равна
угол
наименьшим быть не может: иначе сумма углов треугольника выходит больше или
меньше
Таким образом, имеем
Тогда, поскольку
то точка
обязательно лежит вне
треугольника.
Обозначим
![]()
Из суммы углов треугольника имеем
Запишем теорему синусов для
По теореме синусов для
Поскольку и
получаем
Докажем, что
Треугольник равнобедренный
Также имеем
так как
равнобедренный. Так
как
то
Из суммы углов треугольника
получаем
Из суммы углов треугольника
получаем
эквивалентно
а это равенство мы уже проверили. Тогда
поэтому
Так как
то по сумме углов в
откуда
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике где
на сторонах
и
отмечены точки
и
соответственно так, что
Докажите, что центр описанной окружности треугольника
лежит на биссектрисе угла
Источники:
Пусть — центр описанной окружности треугольника
и
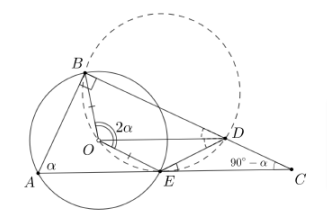
Тогда
Значит, четырёхугольник BOED вписанный. Так что углы и
равны, как вписанные, опирающиеся на равные хорды
.
Ошибка.
Попробуйте повторить позже
Вершину параллелограмма
соединили с серединой
стороны
. Известно, что угол
равен
. Докажите, что
перпендикуляр
на прямую
равен одной из сторон параллелограмма.
Продлим до пересечения с
в точке
. Тогда
, а значит,
по
стороне и двум прилежащим к ней углам, откуда
, а ещё
как противоположные стороны параллелограмма.
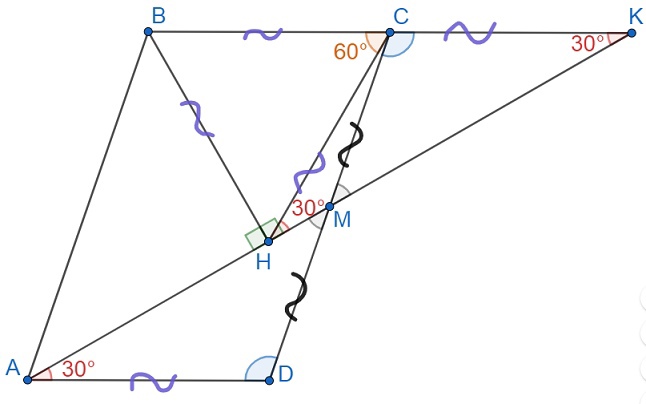
Первый способ.
В прямоугольном проведём медиану
к гипотенузе, тогда
. В силу параллельности
.
— равнобедренный, тогда
, откуда
как внешний угол
. Заметим, что
—
равнобедренный с углом
, а значит, равносторонний,
______________________________________________________________________________________________________________________________________________________
Второй способ.
В прямоугольном катет
напротив угла в
градусов равен половине гипотенузы
, так что равен одной из
сторон параллелограмма.
Ошибка.
Попробуйте повторить позже
Гипотенуза прямоугольного треугольника
равна
Через середину
его катета
провели прямую,
которая делит гипотенузу в отношении
считая от вершины
Найдите отрезок данной прямой, заключённый внутри
треугольника.
Подсказка 1
М - уже середина катета. Пусть точка, которая делит гипотенузу 1к3 - Е. Давайте попробуем отметить середину гипотенузы и провести среднюю линию между ними!
Подсказка 2
Она разделит AB пополам, а как разделится половина гипотенузы, содержащая точку Е?
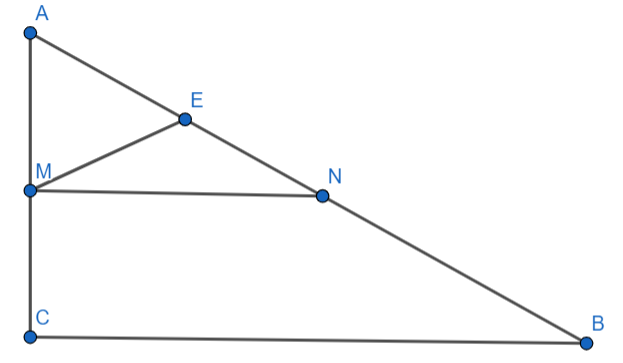
Пусть точка на отрезке
делит его в отношении
Проведём среднюю линию
отсюда
прямоугольный и
— его медиана, то есть
Ошибка.
Попробуйте повторить позже
На стороне треугольника
отметили точки
и
так, что
и
Докажите, что отрезок
виден из
середины
стороны
под прямым углом.
Замечание. Отрезок виден из точки
под углом
Подсказка 1
Доказывать прямоугольность треугольника очень удобно через факт о том, что медиана равна половине гипотенузы - попробуйте найти здесь применение для этого признака.
Подсказка 2
Для этого нужно, конечно, провести медиану MN к предполагаемой гипотенузе (мы пока не доказали, что треугольник прямоугольный, только хотим это доказать). Если отметить все равные отрезки, можно заметить, что у нас еще и средняя линия треугольника таким образом появилась - MN, тоже полезный объект!
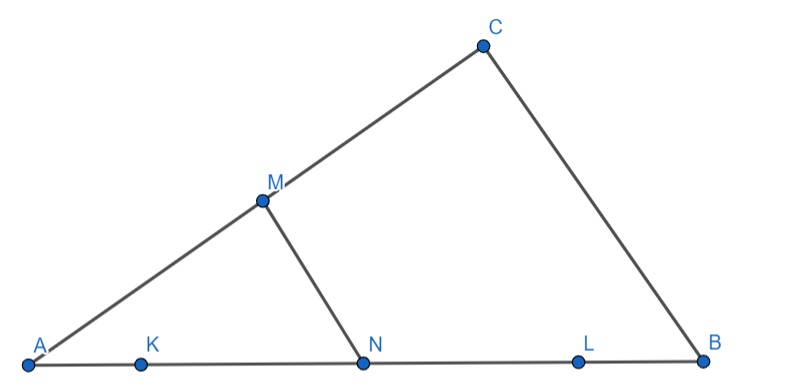
Заметим, что обозначения и
симметричны, потому можем считать, что
лежит между
и
Пусть
— середина
но
из
она также будет серединой
осталось заметить, что
откуда
и
прямой.



