Тема Четырёхугольники

Средняя линия четырёхугольника и прямая Ньютона

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела четырёхугольники

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83840

Две противоположные стороны четырёхугольника равны $1$ . Найдите среднюю линию, соединяющую середины двух других его сторон, если сумма углов при одной из них равна $∘ 60$ .

Показать ответ и решение

Проведём диагональ $BD$ и отметим её середину $M.$

$PIC$

$K$ и $L$ — середины $BC$ и $AD$ соответственно, следовательно, $KM$ и $LM$ — средние линии треугольников $DBC$ и $ABD$ соответственно, тогда

LM = AB-= 1 2 2

KM = CD-= 1 2 2

Т.к. $KM ∥CD$ и $LM ∥AB,$ $∠CBD = ∠KMB$ и $∠BAD = ∠MLD.$ $∠BML$ — внешний угол треугольника $LMD,$ поэтому

∠BML = ∠MLD +∠MDL

Получаем

∘ ∠KML = ∠KMB +∠BML = ∠CDB + ∠MLD + ∠MDL =∠BAD +∠CDA =60

Следовательно, треугольник $KML$ равносторонний, тогда $KL = 1. 2$

Ответ:

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#31336

Две противоположные стороны выпуклого четырехугольника равны и не параллельны. Докажите, что прямая Ньютона данного четырёхугольника образует с этими сторонами равные углы.

Замечание. Прямая Ньютона — это прямая, которая соединяет середины двух диагоналей выпуклого четырёхугольника, отличного от параллелограмма.

Подсказки к задаче

Подсказка 1

Нам уже даны середины диагоналей, поэтому логично рассмотреть ещё и середины сторон. Рассмотрите четырёхугольник с вершинами в серединах диагоналей и в серединах двух неравных сторон. Что вы можете про него сказать?

Подсказка 2

Это ромб! Ведь его стороны являются средними линиями соответствующих треугольников.

Подсказка 3

Что мы знаем про диагональ ромба?

Подсказка 4

Она составляет равные углы с его сторонами! А теперь поймите, как связаны его стороны со сторонами исходного четырёхугольника, и задача решится.

Показать доказательство

Пусть $M$ , $K$ , $X$ , $Y$ — середины $AB$ , $CD$ , $AC$ и $BD$ в четырёхугольнике $ABCD$ , где $AD =BC = a$ .

Проведём средние линии треугольников $ABD$ и $ACD$ , параллельные $AD$ — их длина будет $a 2$ , аналогично длина средних линий $MX$ и $XK$ также будет $a 2$ .

$PIC$

В итоге $MY KX$ — ромб, в котором $XY$ , соединяющая середины диагоналей четырёхугольника, — диагональ, тогда она образует равные углы со сторонами $MY$ и $MX$ , а раз так, то и с параллельными им $AD$ и $BC.$

Ошибка.
Попробуйте повторить позже

Задача 3#75197

В четырёхугольнике $ABCD$ углы $A$ и $C$ — не острые. На сторонах $AB,BC,CD$ и $DA$ отмечены точки $K,L,M$ и $N$ соответственно. Докажите, что периметр четырёхугольника $KLMN$ не меньше удвоенной длины диагонали $AC.$

Подсказки к задаче

Подсказка 1

Попробуем доказать, что отрезок, соединяющий середины противоположных сторон, не больше полусуммы противоположных сторон!

Подсказка 2

Оценивать длины отрезков, пересекающих AC, сложно. Поэтому попробуем использовать доказанное неравенство, отметим середины противоположных сторон во внутреннем четырехугольнике.

Подсказка 3

Попробуем использовать то, что углы A и C - не острые. Если P и Q - середины сторон KN и LM, то что можно сказать о длинах AP и CQ?

Подсказка 4

Длина медианы, проведенной из вершины при неостром угле, не превосходит половины стороны, к которой она проведена! Значит, мы можем оценить AP и CQ, а после - использовать неравенство ломаной, чтобы оценить AC!

Показать доказательство

Лемма. Пусть $M$ и $N$ — середины сторон $AB$ и $CD$ четырехугольника $ABCD$ . Тогда $MN ≤ (AB +CD )∕2.$

Доказательство. Пусть $K$ — середина диагонали $AC.$ Тогда $MK = AB∕2,KN = CD∕2.$

$PIC$

По неравенству треугольника для треугольника $MNK$ имеем:

MN ≤ MK +KN

после подстановки полученных равенств:

MN ≤ AB∕2+ CD ∕2

что завершает доказательство.

Вернемся к решению задачи. Пусть $P$ и $Q$ — середины сторон $KN$ и $LM.$

$PIC$

По лемме $PQ ≤ (KL + MN )∕2.$ Ясно, что длина медианы, проведенной из вершины при неостром угле, не превосходит половины стороны, к котором она проведена, следовательно $AP ≤ KN∕2$ и $LM ∕2.$ Осталось заметить, что по неравенству ломанной верно неравенство

AC ≤ AP +P Q+ QC

Подставляя полученные неравенства имеем

AC ≤ KN ∕2+(KL + MN )∕2+ LM ∕2

домножив данное неравенство на $2,$ получим требуемое.

Ошибка.
Попробуйте повторить позже

Задача 4#31334

В трапеции $ABCD$ с основаниями $AD = a$ и $BC = b$ проведены диагонали $AC$ и $BD$ . Их середины обозначим через $K$ и $M$ соответственно. Чему равен отрезок $KM$ ? Ответ выразите через $a$ и $b$ .

Подсказки к задаче

Подсказка 1

Сразу будем считать, что a>=b. Мы знаем что K и M это середины диагоналей. Какая хорошая прямая в трапеции может проходить через эти точки?)

Подсказка 2

Да, средняя линия трапеции! Пусть её точка на отрезке AB это X, а на отрезке CD это Y. Как можно выразить XK и MY?

Подсказка 3

Стоит воспользоваться тем, что XK например параллельна BC и найти подобие)

Подсказка 4

Да, XK = b/2! аналогично можно найти MY, вспомнить чему равно XY и найти KM)

Показать ответ и решение

Пусть $a ≥b$ . Проведём среднюю линию трапеции $YG$ , как на чертеже:

$PIC$

Она проходит через точки $K$ и $M$ , тогда

YG = a+-b, 2

а также

GM = KY = BC- =-b, 2 2

то есть

a+-b a−-b KM = 2 − b= 2

В случае $b> a$ всё аналогично, а чтобы объединить случаи, можно просто поставить модуль:

|a-− b| KM = 2

Ответ:

$|a−-b| 2$

Ошибка.
Попробуйте повторить позже

Задача 5#31337

Диагонали четырёхугольника равны, а одна из его средних линий в два раза короче каждой из них. Найдите угол между диагоналями.

Замечание. Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.

Подсказки к задаче

Подсказка 1

Нам уже даны середины двух противоположных сторон четырёхугольника, поэтому давайте рассмотрим ещё середину его третьей стороны и получившийся треугольник из трёх середин. Чем он хорош?

Подсказка 2

Этот треугольник правильный, потому что все его стороны равны половине диагонали!

Подсказка 3

А теперь остаётся понять, как связаны углы этого треугольника с углом между диагоналями, и задача решится.

Показать ответ и решение

Пусть в четырёхугольнике $ABCD$ средняя линия $EG$ равна половине каждой диагонали. Пусть также $F$ — середина $AD$ .

$PIC$

Тогда угол между средними линиями $EF$ и $FG$ треугольников $ABD$ и $ACD$ равен углу между диагоналями, а сами они равны $EG$ , поскольку в два раза меньше диагоналей, но отсюда $EFG$ — правильный, а значит, $∠EFG = ∠(AC, BD)= 60∘$ .

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 6#47141

Центроидом четырехугольника будем называть точку пересечения двух прямых, соединяющих середины его противоположных сторон. Шестиугольник $ABCDEF$ вписан в окружность $Ω$ с центром $O.$ Известно, что $AB = DE$ и $BC = EF.$ Пусть $X, Y$ и $Z$ — центроиды четырехугольников $ABDE, BCEF$ и $CDF A$ соответственно. Докажите, что высоты треугольника $XYZ$ пересекаются в точке $O.$

Источники: КМО - 2018, четвёртая задача первого дня для 8-9 классов, авторы Полянский А.А. и Jiang Z. (cmo.adygmath.ru)

Подсказки к задаче

Подсказка 1

Сначала хочется разобраться с равенствами сторон. Заметим, что в силу этих равенств три четырёхугольника из условия являются равнобедренными трапециями! Тогда у них равны диагонали. Что тогда можно сказать про связь этих диагоналей с центром O?

Подсказка 2

Правильно, они равноудалены от O. Тогда их середины P, Q, R равноудалены от O, т.е. O является центром описанной окружности △PQR. Почему это хорошее наблюдение? Ну, кажется, что центроиды как-то связаны со сторонами △PQR.

Подсказка 3

Действительно, из симметрии трапеций центроиды вроде бы должны быть серединами соответствующих сторон △PQR. На самом деле это правда, попробуйте доказать это утверждение в таком виде: середины сторон △PQR являются центроидами соответствующих трапеций. Этот факт верен и для произвольного четырёхугольника, попробуйте его также доказать, это довольно важная лемма. Теперь, когда мы доказали эту крутую лемму, поймём, как связаны △PQR и △XYZ.

Подсказка 4

Стороны △XYZ являются средними линиями △PQR, т.е. параллельны его сторонам. Постойте, но теперь утверждение задачи очевидно! Ведь т.к. O является центром описанной окружности △PQR, то мы можем провести серединные перпендикуляры. А ведь для △XYZ они являются... :)

Показать доказательство

Важная лемма о центроиде. Центроид четырехугольника является серединой отрезка, соединяющего середины его диагоналей.

Первый способ доказательства. Пусть $A1A2A3A4$ — данный четырехугольник, а $Mij$ — середина отрезка $AiAj$ (для всех пар индексов). Тогда $M12M13$ — средняя линия треугольника $A1A2A3,$ поэтому $M12M13 ∥ A2A3.$ Аналогично $M42M43 ∥A2A3,$ поэтому $M12M13 ∥M42M43.$ Таким же образом доказывается параллельность $M12M42$ и $M13M43.$ Значит, $M12M13M43M42$ — параллелограмм, тем самым середина отрезка $M13M24$ лежит на прямой $M12M34.$ Аналогично, середина $M13M24$ лежит на прямой $M23M41,$ таким образом, эта середина является центроидом. Утверждение доказано.

Второй способ доказательства. Пусть у четырёхугольника $ABDE$ точки $P,Q$ — середины $AD,BE$ . Пусть $M,N,K,L$ — середины $AB,BD, DE,EA.$ Для центроида $X$ выполнено $MX =XK,$ поскольку $MNKL$ — параллелограмм. Заметим, что $MP ∥BC ∥ QK,$ а также $MP = QK = B2C,$ откуда $−−→ −−→ MP = QK.$ Тогда уже для $X ′$ — середины $PQ$ получаем

−−−→′ −−M→P-+-−−M→Q- −M−Q→-+−Q−→K- −−M→K-- −−→ MX = 2 = 2 = 2 = MX

Отсюда $′ X =X .$ Утверждение доказано.

$PIC$

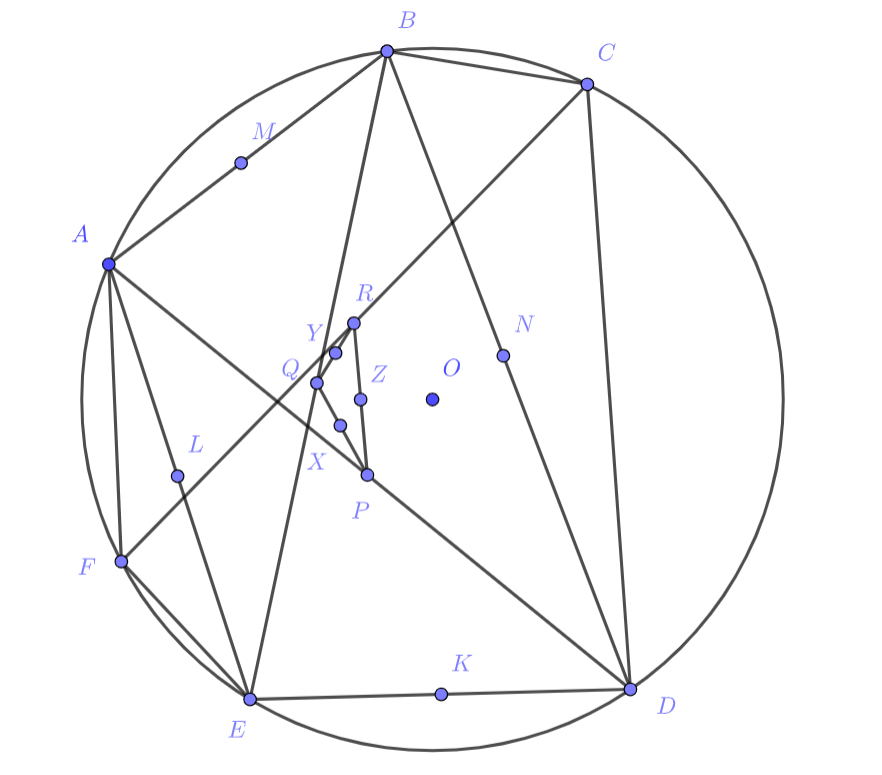
Решение. Проведем диагонали $AD,BE,CF ;$ пусть $P,Q,R$ соответственно — их середины. По Важной лемме о центроиде середины отрезков $PQ,QR, RP$ и есть центроиды четырехугольников $ABDE, BCEF, CDF A.$ Итак, $X,Y,Z$ — соответственно середины отрезков $P Q,QR, RP.$

Из равенства отрезков $AB =DE$ и $BC = EF$ следует равенство дуг, откуда $AD =BE =CF,$ отсюда $P,Q$ и $R$ равноудалены от $O.$ Тогда $OX$ — серединный перпендикуляр к $P Q.$ Так как $Y Z∥PQ$ как средняя линия, то $OX ⊥ YZ.$ Аналогично $OY ⊥ XZ,$ значит, $O$ — ортоцентр треугольника $XY Z.$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#39610

В выпуклом четырёхугольнике $ABCD$ прямые $AD$ и $BC$ перпендикулярны, а длина отрезка, соединяющего середины диагоналей $BD$ и $AC$ , равна $2013$ . Найдите длину отрезка, соединяющего середины сторон $CD$ и $AB$ .

Источники: ОММО-2013, номер 4, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть K,L,M,N-середины AB,AC,CD,BD. Тогда, к примеру в треугольнике ABC у нас есть две середины сторон. На проведение какого(каких?) доп.построения это может намекать?

Подсказка 2

Отлично, мы провели 4 средние линии. Но ведь средняя линия параллельна стороне треугольника! Тогда что можно сказать про ч-угольник KLMN , используя условие, что AD перпендикулярно BC?

Подсказка 3

Да, то что KLMN-прямоугольник. Дело остается за малым, ведь осталось лишь применить одно свойство прямоугольника, чтобы найти KM

Показать ответ и решение

$PIC$

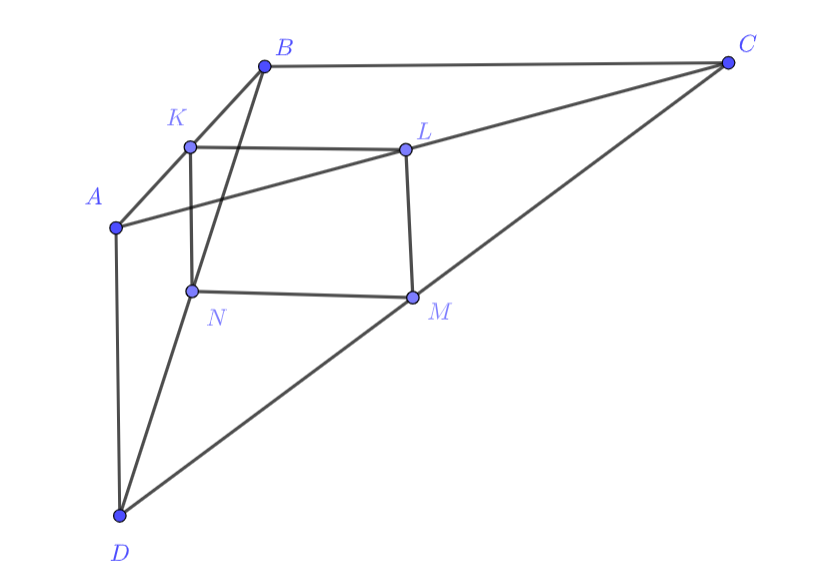
Первое решение.

Пусть $K,L,M, N$ — середины $AB,AC,CD,BD$ соответственно. Заметим, что $KL ∥NM ∥ BC$ , как средние линии в $△ABC, △BDC$ . Аналогично $KL ∥MN ∥AD$ . Отсюда $KLMN$ — параллелограмм, в котором $KL ⊥ ML$ в силу $BC ⊥ AD$ , то есть это прямоугольник, в котором диагонали равны. Осталось заметить, что его диагоналями и будут два отрезка из условия.