Тема 3. Геометрия в пространстве (стереометрия)

3.07 Призма

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела геометрия в пространстве (стереометрия)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#17132

От треугольной призмы, объем которой равен 120, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

$PIC$

Показать ответ и решение

Обозначим через $S$ площадь основания призмы, через $h$ — ее высоту. Тогда объем призмы равен

Vпр =Sh = 120

Объем отсеченной пирамиды равен

1 Vпир = 3Sh =40

Тогда объем оставшейся части равен

Vост = Vпр − Vпир = 120− 40= 80

Ответ: 80

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#17753

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

$PIC$

Показать ответ и решение

Пусть $S$ — площадь основания треугольной призмы, а $h$ — ее высота. Тогда объем треугольной призмы равен $V = Sh.$

Рассмотрим отсеченную призму. Ее высота равна высоте изначальной треугольной призмы, то есть равна $h.$ Так как $MN$ — средняя линия треугольника $ABC,$ то треугольник $AMN,$ лежащий в основании отсеченной призмы, подобен с коэффициентом $1 2$ треугольнику $ABC,$ лежащему в основании изначальной призмы, по отношению сторон $AM :AB = AN :AC =1 :2$ и общему углу между ними. Тогда площадь треугольника $AMN$ в $2 2 = 4$ раза меньше площади треугольника $ABC.$

Значит, объем отсеченной призмы равен

Vo = 1 Sh= 1V ⇒ V = 4Vo = 4⋅5= 20 4 4

Ответ: 20

Ошибка.
Попробуйте повторить позже

Задача 3#18126

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсечённой треугольной призмы равен 7.

$PIC$

Показать ответ и решение

Пусть $S$ — площадь основания треугольной призмы, а $h$ — ее высота. Тогда объем треугольной призмы равен

V = Sh

Рассмотрим отсеченную призму. Ее высота равна высоте изначальной треугольной призмы, то есть равна $h$ . Отрезок $MN$ — средняя линия треугольника $△ ABC$ , поэтому треугольник $△ AMN$ , лежащий в основании отсеченной призмы, подобен треугольнику $△ ABC$ , лежащему в основании изначальной призмы. Это следует из отношения сторон

AM :AB = AN :AC = 1:2

и общего угла $∠A$ .

Тогда площадь треугольника $△ AMN$ в $22 = 4$ раза меньше площади треугольника $△ ABC$ и объем отсеченной призмы равен

Vотс = 1Sh = 1V 4 4

Отсюда объем исходной призмы равен

V = 4Vотс = 4⋅7 =28

Ответ: 28

Ошибка.
Попробуйте повторить позже

Задача 4#2340

$ABCA1B1C1$ – треугольная призма с основаниями $ABC$ и $A1B1C1$ . Отрезок $A1K$ перпендикулярен плоскости $(ABC )$ , $A1K = 3$ , причем точка $K$ лежит на медиане $AM$ треугольника $ABC$ , $AK = 0,2AB$ , $AB = AC$ , $-- BC = 10√ 3$ . Найдите угол между плоскостями $(ABC )$ и $(AA1C )$ . Ответ дайте в градусах.

Показать ответ и решение

Построим $KP$ перпендикулярно $AC$ .

$PIC$

Тогда $A1P$ перпендикулярен $AC$ по теореме о трех перпендикулярах и угол между плоскостями $(ABC )$ и $(AA1C )$ равен $∠A1P K$ .

Так как $AB = AC$ и $AM$ – медиана, то треугольник $ABC$ равнобедренный и $AM$ – высота. Треугольники $AP K$ и $AM C$ подобны по двум углам ( $∠P AK$ – общий), тогда

P K AK 1 -----= ---- = 0,2 = -. M C AC 5

Так как $1- √ -- M C = 2BC = 5 3$ , то $√ -- P K = 3$ .

A1K 3 √ -- tg∠A1P K = ----- = √---= 3 ⇒ ∠A1P K = 60 ∘, PK 3

так как $0∘ < ∠A1P K < 180∘$ .

Ответ: 60

Ошибка.
Попробуйте повторить позже

Задача 5#2768

В основаниях призмы $ABCDEF A1B1C1D1E1F1$ лежат правильные шестиугольники. $AD$ и $BF$ пересекаются в точке $H$ , $A1H$ – высота призмы. Ребро $AA1$ наклонено к плоскости оснований под углом, тангенс которого равен $2$ . Найдите объем призмы, если $-- AF = 2√ 3$ .

$PIC$

Показать ответ и решение

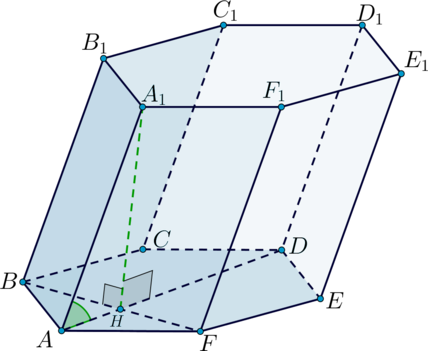
$AH$ – проекция наклонной $A1A$ на плоскость $ABC$ , тогда $tg∠A1AH = 2$ .

В $ABCDEF$ все углы равны друг другу, их можно найти по формуле: $180∘⋅(n−-2)- 6$ , где $n$ – число сторон правильного многоугольника, тогда каждый угол в правильном шестиугольнике равен: $180∘⋅(6−2) ----6--- = 120∘$ .

Треугольник $△ABF$ – равнобедренный, $180∘−-120∘ ∘ ∠ABF = ∠AF B = 2 = 30$ .
В силу симметрии $ABCDEF$ : $120∘ ∠F AH = ∠BAH = -2--= 60 ∘$ $⇒$ $△AHF$ – прямоугольный. В этом треугольнике $AH$ лежит напротив угла в $30∘$ $⇒$ $√ -- AH = 1⋅ AF = 1 ⋅ 2 3 2 2$ .
В прямоугольном треугольнике $△A1AH$ : $√ -- A1H = AH ⋅ tg∠A1AH = 2 3$ .

В шестиугольнике $ABCDEF$ отрезки $AD$ , $BE$ и $CF$ пересекаются в точке $O$ , при этом шестиугольник разделится на $6$ одинаковых равносторонних треугольников со стороной, равной $2√3--$ (см. рисунок).

$PIC$

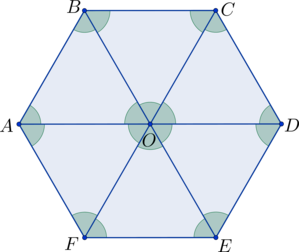
Тогда $1 √ -- √ -- ∘ 1 √ -- √ -- √3- √ -- SABCDEF = 6 ⋅ S тр. = 6 ⋅2 ⋅ 2 3 ⋅ 2 3 ⋅ sin60 = 6 ⋅ 2 ⋅ 2 3 ⋅ 2 3 ⋅ 2 = 18 3$ .

Теперь найдем объем призмы:

√ -- √ -- V = A1H ⋅ SABCDEF = 2 3 ⋅ 18 3 = 108.

Ответ: 108

Ошибка.
Попробуйте повторить позже

Задача 6#40595

Площадь боковой поверхности треугольной призмы равна 36. Через среднюю линию основания этой призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсечённой треугольной призмы.

$PIC$

Показать ответ и решение

Обозначим площадь боковой поверхности исходной призмы за $Sисх.,$ площадь боковой поверхности отсеченной призмы за $Sотс..$

Площадь боковой поверхности исходной призмы равна:

Sисх. = SA BBA + SB CCB + SA CCA 1 1 1 1 1 1

Площадь боковой поверхности отсеченной призмы равна:

S = S +S +S отс. A1M1MA M1N1NM A1N1NA

Так как $MN$ — средняя линия $△ ABC,$ то

1 MN = 2BC 1 AM = MB = 2AB 1 AN = NC = 2AC

В параллелограммах $A1M1MA$ и $A1B1BA$ высоты, проведенные к основаниям $AM$ и $AB$ совпадают, а основание $AM$ в 2 раза меньше основания $AB.$ Так как площадь параллелограмма равна произведению высоты на основание, то:

SA M MA = 1SA B BA 1 1 2 1 1

Аналогично:

1 SM1N1NM = 2SB1C1CB SA1N1NA = 1SA1C1CA 2

Найдем площадь боковой поверхности отсеченной призмы:

Sотс. = SA1M1MA + SM1N1NM +SA1N1NA = = 1SA1B1BA + 1 SB1C1CB + 1SA1C1CA = 1 Sисх. = 18 2 2 2 2

Ответ: 18

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#58793

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

$PIC$

Показать ответ и решение

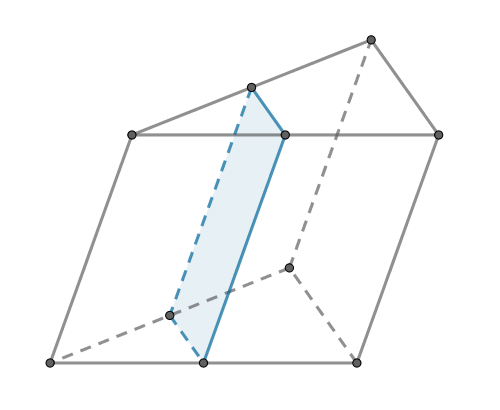
Рассмотрим боковую грань отсеченной треугольной призмы, параллельную одной из боковых граней исходной призмы. Она представляет собой параллелограмм с высотой, равной высоте параллельной ей боковой грани исходной призмы и основанием в 2 раза меньше, чем у грани исходной призмы. Значит, их площади также отличаются в 2 раза.

Две оставшиеся боковые грани отсеченной треугольной призмы являются частями боковых граней исходной призмы. Каждая из них — параллелограмм, у которого одна из сторон равна стороне соответствующей ей грани исходной призмы, а вторая сторона в 2 раза меньше. Значит, их площади также отличаются в 2 раза.

Таким образом, площадь боковой поверхности отсеченной призмы в 2 раза меньше площади боковой поверхности исходной призмы. Тогда площадь боковой поверхности исходной призмы равна

8⋅2= 16

Ответ: 16

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Предыдущий раздел

Следующий раздел