Тема Физтех - задания по годам

Физтех 2013

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела физтех - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31506

Число $84605$ написали семь раз подряд, при этом получилось $35$ -значное число

84605846058460584605846058460584605.

Из этого $35$ -значного числа требуется вычеркнуть две цифры так, чтобы полученное после вычёркивания $33$ -значное число делилось на $15$ . Сколькими способами это можно сделать?

Источники: Физтех-2013, 11.4 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Нужно, чтобы наше число делилось на 15. Значит чего необходимо и достаточно? Как этого добиться? Верно, нужно, чтобы число делилось на 3 и на 5.

Подсказка 2

Чтобы число делилось на 5 нужно, чтобы последняя цифра была либо 5 либо 0. Значит нельзя вычеркнуть две последние цифры одновременно. Делимость на 3 обеспечивается суммой цифр. Сумма цифр вполне понятна. Тогда на что лучше заменить каждую из цифр в числе?

Подсказка 3

Верно, на остаток по модулю 3. Тогда, чтобы число делилось на 3, нужно вычеркнуть либо 2 единицы, либо ноль и двойку. Осталось учесть, что один из вариантов нам не подходит (так как нельзя вычеркнуть последние две цифры одновременно), и посчитать количество вариантов по каждому случаю.

Показать ответ и решение

Для того, чтобы число делилось на $15,$ необходимо и достаточно, чтобы оно делилось на $3$ и на $5$ . Для делимости на $5$ нужно, чтобы последняя цифра числа была $0$ или $5.$ Значит, полученное число будет делиться на $5,$ если мы вычеркнем любые две цифры, кроме двух последних. Перейдём к делимости на $3$ .

Если в числе заменить все цифры $8$ и $5$ на $2$ , цифры $4$ на $1,$ а цифры $6$ на $0,$ то остаток от деления числа на $3$ не изменится (остаток от деления числа на $3$ равен остатку от деления суммы цифр этого числа на $3$ ). Нужно узнать, сколькими способами можно вычеркнуть две цифры из числа $X = 21002210022100221002210022100221002$ так, чтобы полученное число делилось на $3$ . Сумма цифр числа $X$ равна $35$ . Чтобы после вычёркивания сумма цифр делилась на $3$ , мы можем вычеркнуть либо а) две единицы, либо б) двойку и ноль.

а) Количество способов вычеркнуть две единицы равно $2 C7 = 21$

б) Количество способов вычеркнуть один ноль и одну двойку равно $C114⋅C114 =14⋅14= 196.$

Но в пункте (б) мы подсчитали способ, при котором вычеркнуты последние две цифры. Такого допускать нельзя, чтобы не нарушить делимость на $5$ . Этот способ нужно вычесть. Так что в итоге получаем $21+ 196− 1= 216$ способов.

Ответ:

$216$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#31510

Найдите количество прямоугольников со сторонами, параллельными осям координат, таких, что точка $(14;22)$ содержится внутри (но не на границе) каждого из них, абсциссы вершин являются натуральными числами меньше $29$ , а ординаты — натуральны и меньше, чем $31$ .

Источники: Физтех-2013, 11 (см. fizteh2013.ru)

Подсказки к задаче

Подсказка 1

Прямоугольник задаётся четырьмя прямыми. Каким условиям должны удовлетворять эти прямые, чтобы точка (14, 22) была внутри? А чтобы при этом выполнялись ограничения на абциссу и ординату?

Подсказка 2

0 < a < 14 < b < 29, 0 < c < 22 < d < 31, где a,b — абсциссы вертикальных границ фигуры, c, d — ординаты горизонтальных границ прямоугольника! Сколько вариантов у нас есть для a? А для b?

Показать ответ и решение

Прямоугольник можно задать 4 прямыми вида $x= a$ , $x= b$ , $y = c$ , $y = d$ . Пусть не умаляя общности $a< b$ и $c< d$ . По условию $0 <a <14< b< 29$ и $0<c <22< d< 31$ . Отсюда для $a$ у нас 13 вариантов, для $b$ у нас $28 − 14= 14$ вариантов, для $c$ у нас 21 вариант и для $d$ у нас $30− 22= 8$ вариантов.

Получаем ответ $13⋅14 ⋅21⋅8 =30576$ .

Ответ:

$30576$

Ошибка.
Попробуйте повторить позже

Задача 3#38131

Решите уравнение

(2 ) 3 2 log5x x +9x+ 15 +log125x x = x.

Источники: Физтех-2013, 11.1 (см.olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

У нас в основании логарифмов пятерки в некоторых степенях. А это как-то можно исправить? Когда в основании логарифма показательная функция работать не так удобно, как с константой там же.

Подсказка 2

Ну конечно, можно. По свойству логарифмов. Что-то мы забыли… Ах, да! Найти ОДЗ! Ведь вынеся степень из основания оно точно будет использоваться.

Подсказка 3

Ого, какое простое ОДЗ, х>0. А значит можно домножить на х и не потерять корней. Теперь у нас остается что сумма наших логарифмов равна 2. Но они по одному основанию! Значит их можно преобразовать в один и приравнять к логарифму по основанию 5, равному двойке.

Подсказка 4

В итоге получаем кубическое уравнение, которое остается решить (к примеру угадать один из корней) и не забыть учесть ОДЗ.

Показать ответ и решение

ОДЗ:

x> 0

Вынесем из оснований и аргументов логарифмов показатели степеней, получим

1log (x2+ 9x +15)+ 3-log x = 2 ⇐⇒ log (x3+ 9x2+15x)= log 25 x 5 3x 5 x 5 5

Что эквивалентно равенству

3 2 2 2 x + 9x + 15x− 25= 0 ⇐⇒ (x − 1)(x + 10x+ 25)= 0 ⇐⇒ (x− 1)(x +5) = 0

Получается $x= 1,x =− 5$ , но только $x =1$ входит в ОДЗ исходного уравнения.

Ответ:

$1$

Ошибка.
Попробуйте повторить позже

Задача 4#51630

В основании треугольной пирамиды $SABC$ лежит прямоугольный треугольник $ABC$ с гипотенузой $BC = 2√3$ . Сфера $ω$ касается плоскости основания пирамиды и касается всех трёх её боковых рёбер в их серединах. Пусть $Ω$ — сфера, описанная около пирамиды $SABC.$

(a) Найдите расстояние между центрами сфер $ω$ и $Ω$ .

(b) Найдите отношение радиусов сфер $ω$ и $Ω$ .

Подсказки к задаче

Пункт а, подсказка 1

Пусть центр сферы ω — точку O. Где он будет находиться?

Пункт а, подсказка 2

Чему будет равно расстояние от него до вершин пирамиды?

Пункт а, подсказка 3

Рассмотрите серединные перпендикуляры к рёбрам пирамиды.

Пункт б, подсказка 1

Какие есть прямоугольные треугольники на картинке?

Пункт б, подсказка 2

Рассмотрите треугольники SOK, SOL и SOM.

Пункт б, подсказка 3

Докажите, что боковые ребра пирамиды равны между собой.

Пункт б, подсказка 4

Через какую точку пройдет высота пирамиды?

Пункт б подсказка 5

Через центр окружности, описанной около основания. Воспользуйтесь тем, что треугольник ABC — прямоугольный.

Пункт б, подсказка 6

Найдите отрезок, равный радиусу сферы ω.

Пункт с, подсказка 1

Каким будет треугольник SAB?

Пункт с, подсказка 2

Равнобедренным, а треугольник SBC?

Показать ответ и решение

$PIC$

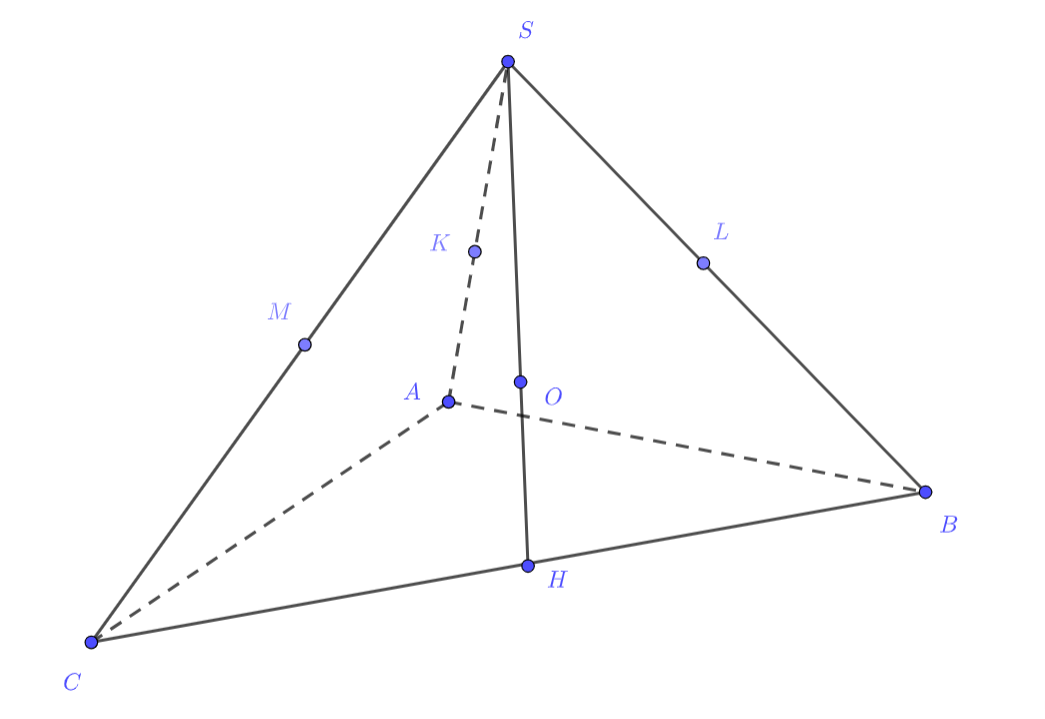
Пусть $O$ — центр сферы $ω;K,L,M$ — основания перпендикуляров, опущенных из точки $O$ на ребра $AS,BS,CS$ соответственно; $SH$ — высота пирамиды $SABC; r$ и $R$ — радиусы сфер $ω$ и $Ω$ соответственно.

a) Поскольку точка $O$ лежит на серединном перпендикуляре к отрезку $AS,$ она равноудалена от концов этого отрезка, т.е. $OA =OS.$ Аналогично $OB =OS$ и $OC =OS.$ Значит, $OA = OB =OC = OS,$ поэтому точка $O$ является центром сферы $Ω$ . Следовательно, расстояние между центрами сфер равно нулю.

b) Из равенства прямоугольных треугольников $SOK$ , $SOL$ и $SOM$ $(OK = OL = OM = r,OS$ — общая сторона) следует, что $SK = SL =SM.$ Поскольку точки $K, L,M$ — это середины боковых рёбер пирамиды, отсюда получаем, что боковые рёбра равны между собой. Тогда высота пирамиды проходит через центр окружности, описанной около основания (действительно, $ΔSHA =ΔSHB = ΔSHC$ по катету и гипотенузе, откуда $AH = BH = CH$ ). Но в пирамиде $OABC$ боковые рёбра $OA, OB,OC$ также равны между собой как радиусы сферы $Ω$ ; значит, и её высота, проведённая из вершины $O$ проходит через центр окружности, описанной около основания. Таким образом, высота пирамиды $SH$ проходит через точку $O.$ Кроме того, точка $H$ является центром окружности, описанной около основания. Поскольку треугольник $ABC$ прямоугольный, $H$ — это середина гипотенузы $BC.$ Так как отрезок $OH$ перпендикулярен плоскости основания, он равен радиусу $r$ сферы $ω.$

Для нахождения соотношения между радиусами рассмотрим прямоугольный треугольник $SHC.$ Точка $M$ — середина гипотенузы $SC,$ на катете $SH$ находится точка $O,$ причём $SO = CO =R$ , $OH = OM = r.$ Треугольники $CHO$ , $CMO$ и $SMO$ равны по катету и гипотенузе, следовательно, $CH = CM =SM.$ Значит, $CH = 1SM, ∠HSC = 30∘. 2$ Тогда из треугольника $SOM$ находим, что $r:R = 1:2.$

c) $SC = 2CH = BC =2√3,$ поэтому треугольник $SBC$ — равносторонний, $SH = SB ⋅ √3= 3. 2$ B равнобедренном треугольнике $SAB$ известны боковые стороны $√ - SB =SA = 2 3$ и угол при основании $1 ∠SAB = arccos4.$ Отсюда находим, что $√- AB = 2SA ⋅cos∠SAB = 3$ . По теореме Пифагора для треугольника $ABC$ находим, что $AC =3,$ поэтому $1 √- SABC =2 ⋅3⋅ 3;$ объём пирамиды $V$ равен $1 3√3- 3√3 3 ⋅3⋅ 2 = 2 .$

Ответ:

(a) $0$

(b) $1 :2$

Ошибка.
Попробуйте повторить позже

Задача 5#67700

Решите неравенство

----1----- --1- ∘|x+-2|−-1 ≤5 +x

Подсказки к задаче

Подсказка 1

Возводить сразу в квадрат нехорошо, так как мы не знаем знак правой части. Слева же у нас всегда положительное число из-за корня. Давайте обратим внимание на знак неравенства. А возможно ли вообще такое, что правая часть отрицательная? В чём будет противоречие?

Подсказка 2

Верно, ведь тогда решений просто не будет. Действительно, правая часть меньше нуля, но тогда и левая тоже. Но такое невозможно! Значит, правая часть положительна, откуда получается ограничение на x. Теперь уже можно перемножить крест накрест выражения и возвести в квадрат. У нас получилось квадратное уравнение с простеньким модулем. Что же тогда остаётся сделать?

Подсказка 3

Да, давайте просто рассмотрим два случая раскрытия модуля. Нужно будет решить два раза квадратное неравенство и победа! Только не забудьте про ограничение.

Показать ответ и решение

Если $5 +x <0,$ то неравенство не выполняется, поэтому $x> −5.$ Отсюда обе дроби положительны и неравенство можно переписать в виде

∘-------- 2 5+ x≤ |x+ 2|− 1 ⇐⇒ 25+10x+ x ≤ |x+ 2|− 1

Рассмотрим случаи

$− 5 <x <− 2$ , здесь
$25+ 10x +x2 ≤−x − 3 ⇐ ⇒ x2+ 11x+28≤ 0 ⇐⇒ x∈ [− 7,−4]$
Пересекая с условием, имеем $x∈(−5,−4]$ .
$x ≥− 2$ , тогда
$25+ 10x +x2 ≤ x+ 1 ⇐⇒ x2+ 9x +24≤ 0$
Дискриминант квадратного трёхчлена отрицательный, решений нет.

Ответ:

$(−5,−4]$

Ошибка.
Попробуйте повторить позже

Задача 6#70309

Тест по английскому языку сдавали 10 школьников. Известно, что любые пять школьников ответили вместе на все вопросы, а любые четыре школьника ответили вместе не на все вопросы. При каком наименьшем количестве вопросов теста такое могло случиться?

Подсказки к задаче

Подсказка 1

Переформулируем условие: для любых 4 школьников найдется вопрос, на который ни один из них не ответил.

Подсказка 2

А могут ли не ответить на один и тот же вопрос сразу две четвёрки школьников?

Подсказка 3

Нет, иначе можем получить пятёрку, не ответившую на этот вопрос.

Подсказка 4

Посчитайте количество четвёрок.

Показать ответ и решение

Переформулируем условие: для любых 4 школьников есть вопрос, на который никто не ответил.

Могут ли на один и тот же вопрос не ответить две четверки школьников?

Предположим, что могут. Рассмотрим две различные четверки, не ответившие на один вопрос. Они отличаются хотя бы одним участником, поэтому получаем пятерку различных школьников, не ответивших на вопрос, противоречие.

Итого для любых 4 есть уникальный вопрос, на который никто не ответил. Получаем оценку: количество вопросов не меньше количества четверок.

Количество четверок: $4 C10 = 210$ . Пронумеруем их и сопоставим каждой по вопросу, на который все из четверки не ответили. Так как на каждый вопрос ответили 6 человек, по принципу Дирихле любые пятеро ответили на все вопросы. Получили пример на 210.

Ответ: 210

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#80045

При каких значениях параметра $a$ существует единственная пара чисел $(x;y),$ удовлетворяющая системе неравенств

{ (x2 − xy+ y2)(x2− 36)≥0 |x− 2+ y|+|x− 2 − y|≤ a?

Подсказки к задаче

Подсказка 1

Что можно сказать о выражении x² - xy + y²?

Подсказка 2

Рассмотрите его как квадратный трехчлен относительно x.

Подсказка 3

D = -3y². Проанализируйте, какие значения может принимать x² - xy + y².

Подсказка 4

Разбейте плоскость на 4 области прямыми x - 2 + y = 0 и x - 2 - y = 0.

Показать ответ и решение

Рассмотрим выражение $A (x;y)= x2 − xy+ y2$ как квадратный трёхчлен относительно $x.$ Его дискриминант равен $D = y2− 4y2 = −3y2.$ При $y ⁄= 0$ дискриминант отрицателен, поэтому $A >0.$ Если $y =0,$ то $2 A = x ,$ т.е. $A > 0$ при $x ⁄=0$ и $A = 0$ при $x =0.$ В итоге получаем, что выражение $A(x;y)$ обращается в ноль в точке $(0;0)$ и положительно во всех остальных точках. Следовательно, первое неравенство системы равносильно совокупности $[ 2 2 [ x2− xy +y = 0, ⇔ x= y = 0 x − 36 ≥0 x∈ (−∞; −6]∪[6;+∞ )$ Изобразим множество точек, удовлетворяющих этой совокупности, на координатной плоскости. Получаем все точки, лежащие на прямой $x= −6$ и левее неё, точки на прямой $x =6$ и правее неё, а также точку $(0;0).$

$PIC$

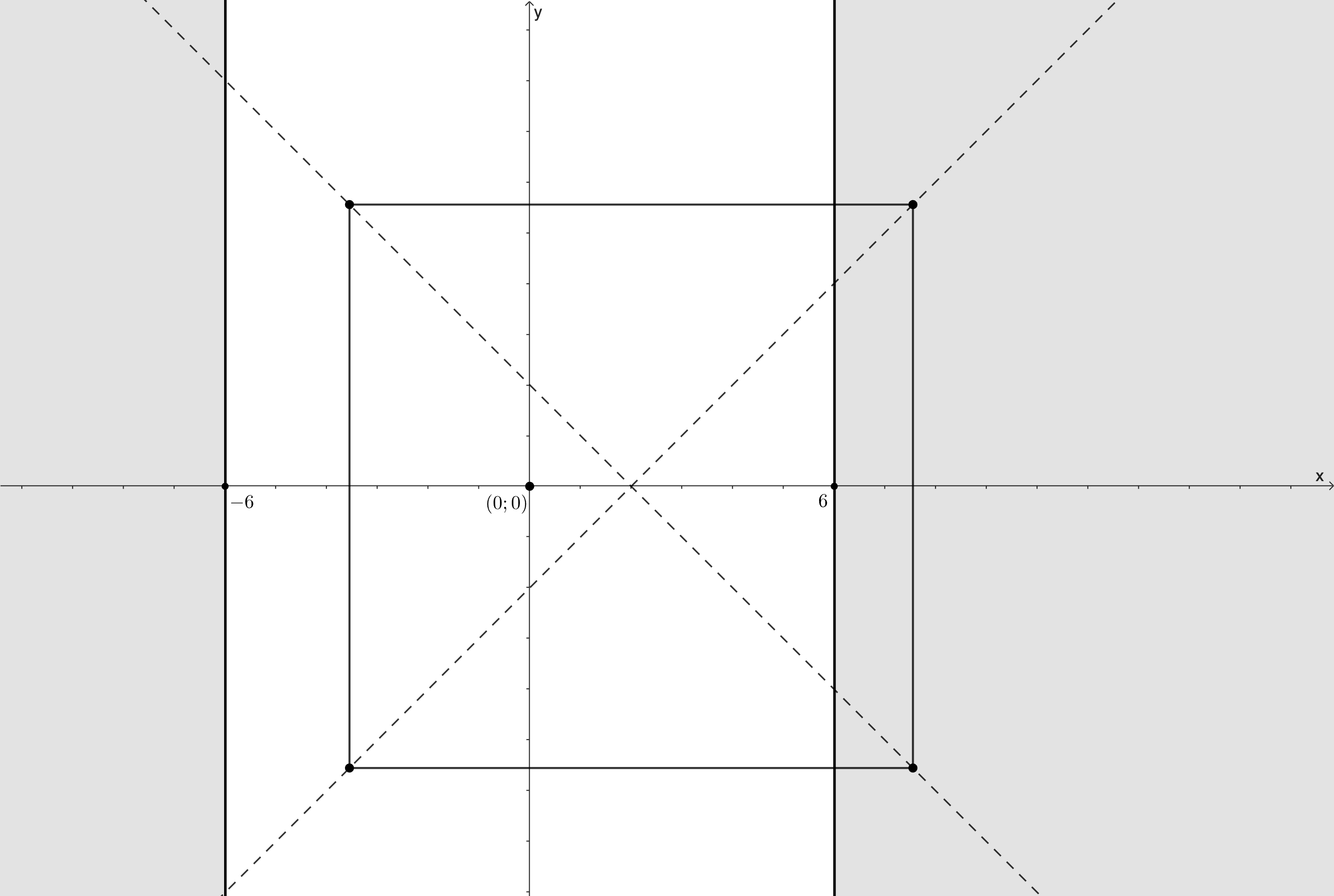
Перейдём ко второму неравенству. Проведём на координатной плоскости прямые $x − 2+ y = 0$ и $x− 2− y = 0.$ Они разбивают плоскость на 4 области, в каждой из которых знаки выражений под модулями постоянны. Рассматриваем 4 случая. Если $x − 2 +y ≥ 0$ и $x− 2− y ≥ 0,$ то неравенство принимает вид $a x− 2+ y+x − 2− y ≤ a⇔ x ≤2 +2$ Аналогично, если $x− 2+ y < 0$ и $x− 2− y ≥0,$ то $a − x +2− y+ x− 2− y ≤ a⇔ y ≥ −2$ . Если $x− 2+y <0$ и $x − 2− y < 0,$ то $a − x +2− y− x+ 2+y ≤a ⇔ x≥ 2− 2$ Если $x− 2 +y ≥0$ и $x− 2− y < 0,$ то $a x− 2+y − x +2+ y ≤ a⇔ y ≤2$ Окончательно получаем, что при $a =0$ неравенство задаёт точку $(2;0),$ при $a >0−$ квадрат с центром в точке $(2;0)$ и стороной $a,$ а при $a< 0−$ пустое множество.

Очевидно, при $a≤ 0$ система не имеет решений. При $a >0$ для того, чтобы было единственное решение, нужно, чтобы точка $(0;0)$ попадала в квадрат, но чтобы квадрат не пересекал прямую $x= 6,$ откуда следует, что $2≤ a2 <4,$ т.e. $4≤ a< 8.$

Ответ:

$4 ≤a< 8$

Ошибка.
Попробуйте повторить позже

Задача 8#101216

При каком наибольшем натуральном значении $n$ число $n!+ 5n +52$ является точным квадратом?

Подсказки к задаче

Подсказка 1

Как можно выявлять точные квадраты?

Подсказка 2

Попробуйте посмотреть на остатки.

Подсказка 3

Например, 5n всегда делится на 5. А что тогда можно сказать про n! ?

Подсказка 4

Если n ≥ 5, то остаток при делении на 5 выражения будет равен 2, но ни один точный квадрат не даёт такой остаток по модулю 5. Осталось рассмотреть n < 5.

Показать ответ и решение

Заметим, что при $n≥ 5$ $n!$ делится на 5. Отсюда

n!+5n+ 52≡ 2 (mod 5)

Рассмотрим таблицу остатков квадратов по модулю 5:


$x$	$x2$

$0$	$0$

$1$	$1$

$2$	$4$

$3$	$4$

$4$	$1$

Из таблицы видно, что квадрат не может давать остаток 2 по модулю 5, а, значит, при $n≥ 5$ число $n!+ 5n +52$ не является квадратом. Осталось рассмотреть $n <5.$

При $n =4 :n!+ 5n+ 52 =24+ 20+ 52 =96$ — не квадрат.

При $n =3 :n!+ 5n+ 52 =6 +15+ 52= 73$ — не квадрат.

При $2 n =2 :n!+ 5n+ 52 =2 +10+ 52= 64 =8$ — квадрат.

Итак, наибольшее натуральное значение $n,$ при котором число $n!+5n +52$ является точным квадратом, равно 2.

Ответ: