Физтех до 2010 и вступительные на Физтех
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Решить уравнение
Подсказка 1
Обратите внимание на то, что в числителях аргумент синуса есть разность аргументов косинуса;) В какой формуле такое присутствует?
Подсказка 2
Вспоминаем формулу разности тангенсов!
Подсказка 3
sin(a-b)/cos(a)cos(b) = tg(a) - tg(b).Во что превратится наше выражение после преобразований?
Подсказка 4
tg(4x) = sin(4x). Когда такое возможно?
Подсказка 4
Распишите тангенс по определению и перенесите всё в одну часть! Полученную совокупность несложно решить:)
Используя формулу преобразуем исходное уравнение в виду
Область допустимых значений определяется условиями
а при на ОДЗ исходное уравнение равносильно уравнению
Уравнение равносильно совокупности уравнений
причем все корни уравнения ворого содержатся среди корней уравнения первого. Из первого следует, что либо и тогда
либо
(и тогда
либо
,
Ошибка.
Попробуйте повторить позже
Подсказка 1
С первым неравенством всё понятно, а чтобы построить график функции из второго неравенства, нужно выделить полные квадраты. Чтобы понять, какие точки удовлетворяют третьему неравенству, нужно рассмотреть части плоскости, на которые 2 прямые её делят, и понять, какие знаки в этих частях имеет каждая из линейных функций. И всё, картинка готова!
Подсказка 2
Не забываем, что площадь сегмента находится как разность площадей соответствующего сектора и треугольника, и на этом знаний нам достаточно. Осталось внимательно найти нужные площади и радоваться жизни!
(a) Первому неравенству удовлетворяют точки, лежащие в квадрате (рис.) с вершинами Площадь
этого квадрата
![]()
(b) Второму неравенству, которое можно записать в виде
удовлетворяют точки, лежащие вне круга радиуса с центром в точке
Площадь заштрихованного на рис. сегмента равна а площадь фигуры, координаты точек которой удовлетворяют первым двум
неравенствам, равна
(c) Прямые и
пересекаются в точке
и проходят соответственно через точки
и
Третьему неравенству удовлетворяют точки двух вертикальных углов с вершиной один их этих углов — угол, образуемый лучами
и
и содержащий точку
Пусть — площадь фигуры, координаты точек которой удовлетворяют всем трем неравенствам системы,
— сумма площадей
треугольников
и
Тогда
Ошибка.
Попробуйте повторить позже
Найти все значения , при которых уравнение
имеет корни, а числа
являются целыми.
Подсказка 1.
Хм-м, когда данное уравнение будет иметь корни? Да, действительно, ведь мы знаем ограничение на левую часть равенства. Действительно, -1 ≤ sin(x) ≤ 1. Получается мы можем выделить отрезок, на котором будем рассматривать значения a, а про остальные значения параметра забыть.
Подсказка 2.
Что же делать теперь? Анализировать функцию с параметром! Давайте проанализируем функцию f(a) = (1 - 4*a) / (27*a⁴). Для того, чтобы определить какие значения она принимает, возьмём её производную, найдём минимум и максимум и поймём, что проверить надо всего несколько значений a.
Уравнение будет иметь корни тогда и только тогда, когда
Далее исследуем функцию на отрезке
Где является точкой минимума. Отсюда
может принимать только значения между
и
. При
этом значения эти достигаются только в точках
и
и нигде более функция целые значения принимать не может.
Ошибка.
Попробуйте повторить позже
Решить систему уравнений
Подсказка 1
В уравнениях слишком много повторяющихся слагаемых ;) давайте тогда сделаем замену, после чего придём к несложной и решаемой системе!
Подсказка 2
Сделайте замену u = sin(x)cos(y), v = cos(x)sin(y). Какие будут u и v в решении?
Подсказка 3
Отлично, теперь нужно сделать обратную замену! А в каких выражениях или формулах встречаются такие u и v?)
Подсказка 4
Попробуйте свести систему к системе на синус суммы и разности!
Полагая
получаем систему уравнений
откуда . Исходная система равносильна каждой из следующих систем:
Откуда уже тривиально выписываются решения.
,
Ошибка.
Попробуйте повторить позже
В кубе с ребром
через точку
параллельно прямой
проведена плоскость
, образующая с прямой
угол,
равный
. Найдите площадь сечения куба плоскостью
и радиус шара, касающегося плоскости
и граней
,
и
.
Подсказка 1
Как можно воспользоваться данным углом?
Подсказка 2
Проведите перпендикуляры к плоскости P из центра основания и точки D.
Подсказка 3
Пусть плоскость P пересекает ребро CC₁ в точке K. Рассмотрите треугольник ACK.
Подсказка 4
Попробуйте понять, на биссектрисе какого угла должен лежать центр шара.
Подсказка 5
Это будет ∠AKC. А где будет находиться проекция центра шара на основание?
Плоскость пересечет грань
куба по прямой
где
ребро
— в некоторой точке
Пусть
—
середина
и
основания перпендикуляров, опущенных соответственно из точек
и
на плоскость
Тогда
так как
и
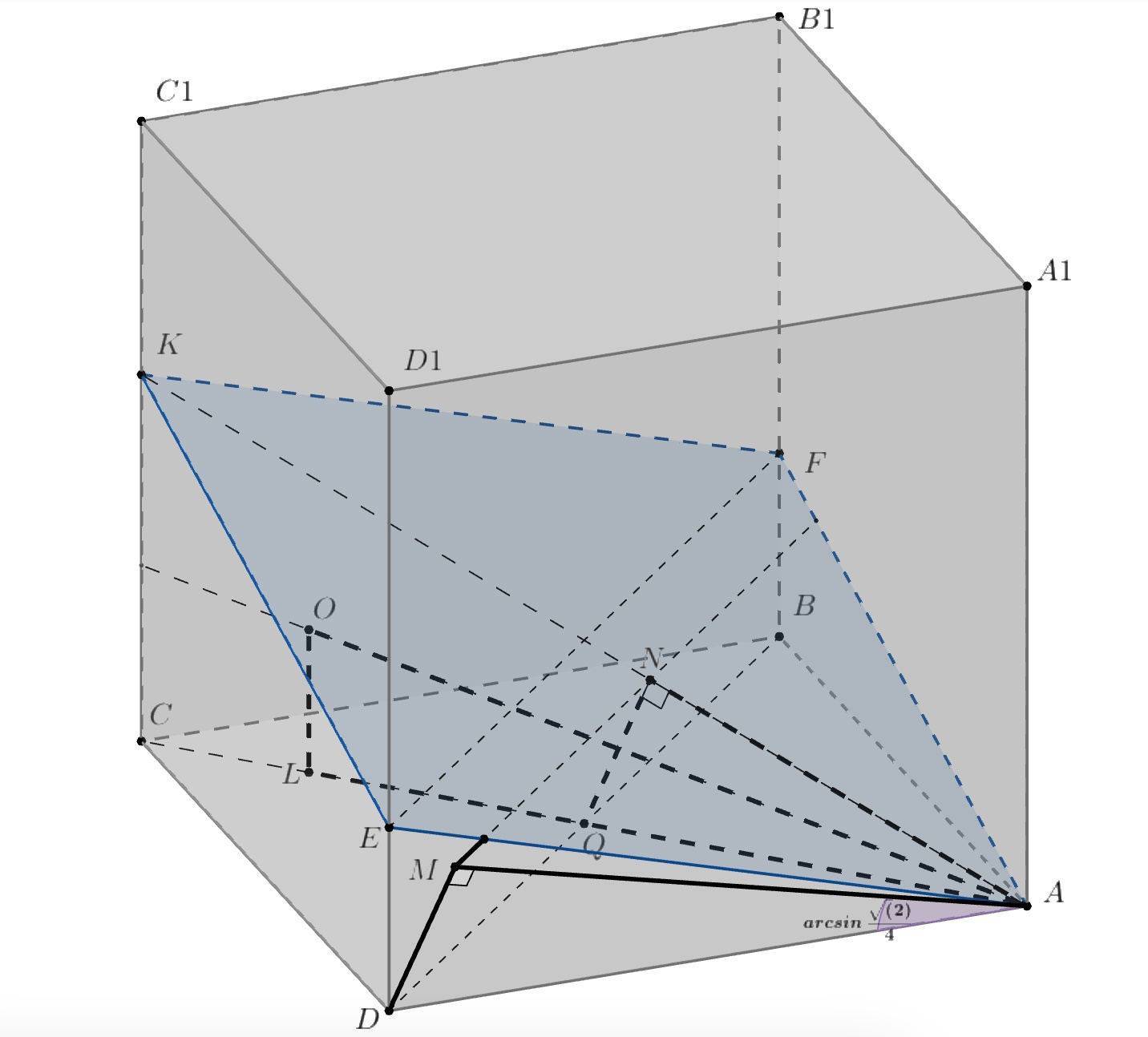
По условию откуда находим
Из треугольника
в котором
находим
и поэтому
Пусть — площадь сечения куба плоскостью
тогда
где
и поэтому
Теперь найдём радиус вписанного шара. Заметим, что центр
шара лежит на биссектрисе угла
, а проекция
точки
на грань
принадлежат
Из треугольника
в котором
находим
где
Так как
тo
_____________________________________________________________________________________
Замечание.
Искомый радиус можно было также найти, заметив что он равен радиусу шара, вписанного в треугольную пирамиду где
— точка пересечения прямых
и
точка пересечения прямых
и
используя формулу
где
— объем
пирамиды
— её полная поверхность.
Ошибка.
Попробуйте повторить позже
Решить уравнение
Источники:
Подсказка 1
Давайте запишем, что правая часть нашего уравнения неотрицательна, и возведем обе части в квадрат.
Подсказка 2
cos(2x) и sin²x легко можно выразить через cos(x), а дальше решить уравнение как квадратное. Когда получите корни, не забудьте про ограничение.
Возведем в квадрат обе части при условии
Из последнего уравнения получаем, что Отсюда получаем серию:
Найденные корни удовлетворяют условию
Ошибка.
Попробуйте повторить позже
В основании призмы лежит прямоугольник
. Острые углы
и
равны между собой,
угол между ребром
и плоскостью основания призмы равен
, а
. Все грани призмы касаются
некоторой сферы. Найти длину
, угол между плоскостями
и
, а также расстояние от точки
до центра
сферы.
Подсказка 1
Что следует из равенства ∠D₁DA и ∠D₁DC?
Подсказка 2
Докажите равенство двугранных углов.
Подсказка 3
Для доказательства этого утверждения можно построить проекцию точки D₁ на плоскость ABCD.
Подсказка 4
Что можно сказать о проекциях центра сферы на грани ABCD и A₁B₁C₁D₁?
Подсказка 5
Расстояния до них будут равны радиусу сферы. Рассмотрите сечения призмы плоскостями, перпендикулярными ребрам AD и DC.
Подсказка 6
Докажите, что полученные сечения являются ромбами.
Подсказка 7
А не является ли ABCD квадратом?
Пусть гдс
— острый угол:
![]()
Тогда двугранные углы при рёбрах и
равны между собой и являются острыми (каждый из этих углов углов обозначим
Для доказательства этого утверждения достаточно построить проекцию точки
на плоскость
затсм
опустить из точки
перпендикуляры на
и
и воспользоваться равенством соответствующих прямоугольных
треугольников.
Пусть — центр вписанной в призму сферы,
и
— проекции точки
на грани
и
Тогда
где
— радиус сферы. Рассмотрим сечения
и
призмы плоскостями, перпендикулярными
рёбрам
и
Фигуры
и
являются параллелограммами, каждый из которых описан около окружности
радиуса
Поэтому фигуры
и
— ромбы, высота каждого из них равна
а острый угол равен
Стороны
этих ромбов равны соответствующим сторонам прямоугольника
и из равенства ромбов следует, что
—
квадрат.
Пусть — проекция точки
на плоскость
тогда
Проведём через
плоскость, перпсндикулярную
и пересекающую
в точке
Тогда
и
— прямоугольные треугольники,
(по
условию),
. Т. к. отрезок
равен стороне ромба, т. е.
, то
Последнее выражение в этой цепочке равно высоте ромба .
Заметим ещё, что точка лежит на диагонали квадрата
и поэтому
где
и поэтому
Отсюда получаем
где
Рассмотрим, наконец, прямоугольные треугольники и
(
— точка, в которой одно из проведённых сечений
пересекает ребро
, т. е. является вершиной одного из построенных ромбов). Т. к. сфера касается граней двугранного угла при ребре
, то
Подставляя найденные значсния и
, находим
.
Ошибка.
Попробуйте повторить позже
Найти все значения параметра при которых сумма всех корней уравнения
меньше
Подсказка 1
Давайте внимательно посмотрим на выражение, поищем общие части в слагаемых. На что похоже это уравнение?
Подсказка 2
На квадратное уравнение относительно y = (x - (9p)/4)². При этом, если мы начнём прямо считать его корни, у нас получатся достаточно громоздкие выражения. Для начала подумаем, а что в целом должно выполняться, чтобы у этого уравнения были корни?
Подсказка 3
Верно, дискриминант должен быть неотрицателен! Запишем его и поймём, при каких р у квадратного уравнения есть корни.
Подсказка 4
Пусть y₁ ≤ y₂ — корни этого квадратного уравнения. Чтобы от них перейти к корням исходного уравнения, нужно решить два других уравнения: (x - (9p)/4)² = y₁ и (x - (9p)/4)² = y₂. Но как теперь перейти к сумме корней? Вспомните, какая теорема связывает сумму корней квадратного уравнения и его коэффициенты.
Подсказка 5
Теорема Виета! Получается, если у уравнения (x - (9p)/4)² = y₁ есть корни, то их сумма равна 9р/2. Заметим, что y₁ * y₂ — это свободный коэффициент исходного квадратного уравнения, пусть он равен С. Осталось понять, какая сумма получается в зависимости от знаков y₁ и y₂, для этого будет удобно рассмотреть случаи: когда С больше нуля, меньше нуля, равно ему, а также когда зануляется дискриминант.
Пусть корни квадратного уравнения
где
Для того чтобы
данное биквадратное уравнение имело решения, необходимо, чтобы дискриминант
был неотрицателен.
Имеем:
т. e. Рассмотрим четыре случая.
первых трех
- 1.
-
тогда
т. е. уравнение
не имеет корней, а уравнение
имеет два различных корня, сумма
которых, согласно теореме Виета, равна
р. Из неравенства
где
следует
и, с учетом условия
получаем
- 2.
-
тогда
или
При
уравнение имеет один корень
и неравенство
выполнено, а при
три корня с суммой
меньшей
.
- 3.
-
тогда
и
одного знака, причем
если
При этом уравнение имеет четыре корня с суммой
поэтому из неравенства
следует
и, с учетом условий
получаем
.
- 4.
-
тогда если
то
и уравнение корней не имеет, а если
то
и
Замечание. Формально, в случае отсутствия корней уравнения (если дискриминант исходного уравнения меньше нуля) про элементы пустого множества решений будет верно любое высказывание, в том числе любая оценка на их сумму. Но авторы вступительных не задумывали грузить этим абитуриентов, предполагая проверку наличия корней.
Ошибка.
Попробуйте повторить позже
Найти все значения параметра , при которых система уравнений
имеет ровно три решения.
Источники:
Подсказка 1
Раз у нас произведение скобок равно нулю, то хоть одна из них равна нулю. Так мы можем свести систему к совокупности из двух систем поменьше) Что можно сказать об уравнениях в каждой из новых систем?
Подсказка 2
Первое уравнение - уравнение окружности, а второе - парабола относительно y. Мы хотим получить три решения, но обычно существуют всякие случаи когда корни из двух случаев пересекаются...Можем ли мы сразу отмести такие варианты?
Подсказка 3
Да! Из второго уравнения мы видим, что x >= 7, что точно не может быть решением первой системы. Теперь давайте снова вернемся к первой системе: на что похоже второе уравнение и как меняется его график при изменении параметра?
Подсказка 4
Если очень внимательно посмотреть, то окажется, что для всех параметров мы получим семейство прямых, которые касаются как раз нашей окружности из первого уравнения! Это можно видеть просто подстановкой из второго уравнения в первое, или по формуле расстояния от точки до прямой. Значит, там всегда одно решение, и осталось понять, когда у нас два решения у второй совокупности)
Система равносительна совокупности
Графиком уравнения является окружность с центром
, радиус которой равен
.
Графиком уравнения является парабола с вершиной
, симметричная относительно оси абсцисс, причем
.
Эти графики не имеют общих точек, следовательно, системы из совокупности общих решений не имеют.
Уравнение задаёт семейство прямых, причём при любом
расстояние от центра окружности
до
прямой равно
радиусу. Поэтому это уравнение задает семейство касательных к окружности.
![]()
Тогда первая система совокупности имеет одно решение при всех . А значит, вторая система должна иметь ровно два
решения.
Если , то
или
При имеем одно решение
; при
получаем
— одно решение.
Следовательно, Тогда вторую систему запишем в виде
Откуда
Это квадратное относительно уравнение будет иметь два решения при положительном дискриминанте.
Тогда , откуда
. Но
, следовательно,
.
Решая эти неравенства, получаем ответ.
Ошибка.
Попробуйте повторить позже
На координатной плоскости даны точки и
При каких значениях параметра
, ближайшая к графику функции
точка прямой
лежит на отрезке
Источники:
Подсказка 1
Для начала надо понять, а почему вообще наша прямая не имеет пересечения на отрезке с нашим графиком (то есть что прямая, которая касается графика не правее нашей), ведь иначе наименьшее расстояние было бы нулевым.
Подсказка 3
Найдите, на какой прямой лежит отрезок AB. При этом ближайшая к графику точка отрезка - это перпендикуляр из точки, в которой параллельная данной прямая касается нашего графика. Значит, надо записать условия касания и понять в какой точке оно происходит.
Подсказка 3
Выходит, что касание происходит в точке x = 1. Теперь, когда мы все нашли, остается понять, какие требования нам нужны, чтобы этот перпендикуляр падал не просто на прямую, а именно на отрезок AB? Что для этого требуется?
Подсказка 4
Чтобы p было таким, что, перпендикуляр падает между точек конца отрезка. Можно найти значения p, когда перпендикуляр попадает на концы отрезка. А все промежуточные p тоже будут подходить.
Для начала поймем, что прямая, проходящая через точки и
, задаётся уравнением
а на области определения функция
не пересекается с
при
потому что минимальное значение разности
достигается при
и равно
Расстояние от точки на графике до прямой это перпендикуляр на прямую
Прямые, перпендикулярные
задаются
уравнением
они параллельны между собой, а наименьшее расстояние достигается при наименьшей длине отрезка
такого перпендикуляра — в точке
касания графика
с прямой, параллельной
Запишем условие касания
функций:
Прямая, перпендикулярная и проходящая через точку
, имеет вид
Прямая, перпендикулярная и проходящая через точку
, задается уравнением
![]()
А проходящая через точку — уравнением
![]()
Отсюда находим подходящие граничные значения Все значения между ними из этого отрезка также
подходят.
Ошибка.
Попробуйте повторить позже
Медиана и биссектриса
прямоугольного треугольника
пересекаются в точке
Найти площадь треугольника
, если
Источники:
Подсказка 1
Сходу непонятно, что делать. У нас имеется медиана, почему бы ее не удвоить...
Подсказка 2
Обозначим за K- точку, симметричную A относительно M. Тогда видно, что треугольники △AOD и △COK подобны с коэффициентом 5/9. Тогда AD/CK=5/9 ⇒ AD/BD=5/4. Можем ли мы найти sin∠A-?
Подсказка 3
По свойству биссектрисы получаем, что sin∠A=BC/AC=4/5. Тогда cos∠A=3/5. Если обозначить AB за 9c, то AC=15c и BD=4с. Тогда из теоремы Пифагора для треугольника △BDC мы можем найти с. Я верю, что и площадь вы легко найдете!
![]()
На продолжении медианы за точку
отложим отрезок
, равный
. Тогда
— параллелограмм.
Обозначим . Треугольники
и
подобны (по двум углам), значит
По свойству биссектрисы треугольника
Поэтому
По теореме Пифагора
Следовательно,
Ошибка.
Попробуйте повторить позже
Биссектриса и высота
остроугольного треугольника
пересекаются в точке
. Окружность радиуса
с центром в точке
проходит через вершину
, середину стороны
и пересекает сторону
в точке
такой, что
. Найти длину
стороны
.
Подсказка 1
Исходя из условия, сразу хочется отметить пересечение луча AD с окружностью за точку F. Для удобства обозначим отрезки на AC с помощью переменной. Как посчитать отрезки на AB?
Подсказка 2
Пусть M — середина стороны AC. AK=AM, значит, BK = 6a, AK = 2a, AE = EM = a, MC = 2a. На что нам намекает равенство углов BAO и OAE, как использовать удвоенный угол и перпендикулярность?
Подсказка 3
Посчитаем косинус BAE! Тогда мы можем посчитать и косинус угла, в два раза меньшего BAE. Выходит, теперь у нас есть косинус угла, противоположного нужной стороне. А как можно найти саму сторону?
Подсказка 4
Найдем a благодаря косинусу и прямоугольному треугольнику! Теперь мы знаем 2 стороны и угол между ними - осталось лишь найти BC
Пусть — середина стороны
–– пересечение продолжения радиуса
с окружностью. Тогда
–– диаметр окружности.
Поскольку
— основание перпендикуляра, опущенного из точки
на хорду
точка
–– середина
Обозначим
Тогда
Точки и
лежат на окружности с диаметром
поэтому
Из равенства прямоугольных треугольников
и
(по гипотенузе и острому углу) следует, что
Тогда
Обозначим
![]()
Из прямоугольного треугольника находим, что
Тогда
Из прямоугольного треугольника находим, что
По теореме косинусов
Ошибка.
Попробуйте повторить позже
Решить уравнение
Источники:
Подсказка 1
Так-с, видим модуль, поэтому первое, что стоит сделать - рассмотреть два случая!
Подсказка 2
Если синус положительный, то можно применить формулу суммы синусов! И дальше получится уравнение, которое решить уже не так и сложно! Теперь разберёмся, когда синус отрицательный!
Подсказка 3
Да, если синус отрицательный, то теперь просто применим формулу разности синусов! И также получим, несложное уравнения, для которого точно сможем найти совокупность решений!
Подсказка 4
И в каждом из случаев - не забывайте про ограничение на синус!
Рассмотрим два случая (1) (2)
(1) При
откуда либо
Отсюда получаем серии:
С учетом неравенства получаем следующие ответы:
(2) При
откуда либо
Отсюда получаем серии:
Объединяя решения последней совокупности с учетом неравенства получаем следующие ответы:
Объединяя ответы из (1) и (2) получаем следующие ответы:
Ошибка.
Попробуйте повторить позже
Подсказка 1
Попробуем преобразовать систему. Что есть схожего у уравнений? Как можно преобразовать левую часть каждого?
Подсказка 2
Левую часть каждого можно разложить на множители, а правые части отличаются домножением на p. Что интересного можно заметить при таком преобразовании? Что хочется с этим сделать?
Подсказка 3
Есть совпадающие скобки, поэтому попробуем поделить одно уравнение на другое. Тогда мы выразим р. А что можно сделать, чтобы благодаря первоначальной системе уравнений найти связь одной из переменных х и у с р? Пока что у нас в каждом уравнении есть все три переменные, как можно избавиться от одной из них?
Подсказка 4
Попробуем найти х/у! Тогда можно будет выразить одну переменную через другую и найти
Подсказка 5
x/y=(2p+1)/(p-3). Как можно оценить р, используя условия на х и у? Теперь, при помощи условия и найденной связи между х и у, мы можем найти квадраты!
Подсказка 6
Сумма квадратов равна (5p^2-2p+10)/(7*(4p^2+9)). Осталось лишь найти экстремумы такой функции на промежутке привычным способом)
Ошибка.
Попробуйте повторить позже
Две параллельные касательные к графику функции пересекают оси координат: первая — в точках
и
, вторая — в точках
и
. Найти площадь треугольника
, если известно, что она в четыре раза меньше площади треүгольника
(
— центр
координат).
Подсказка 1
Пусть касательные касаются графика в точках х₁ и х₂. В условии сказано, что касательные пересекают оси координат, а решение задачи завязано на площадях полученных треугольников. Было бы здорово получить уравнения для нахождения площади каждой фигуры. Как мы можем это вывести?
Подсказка 2
Конечно, на координатной плоскости легко вычислить площадь треугольника, зная координаты его вершин. Их получим из уравнения касательных. Тогда можно легко найти формулы площадей и записать их отношение!
Подсказка 3
Далее вспомните про условие параллельности касательных. Что это нам даёт?
Подсказка 4
Конечно, коэффициенты при х равны! При этом не забывайте, что прямые разные, то есть х₁ и х₂ (точки касания) не равны.
Остаётся только составить систему из этого уравнения и отношения площадей и аккуратно всё посчитать
Пусть — точка касания, тогда
Точки пересечения с осями координат:
Тогда
Так же и для второй точки касания
Эти касательные параллельны, поэтому коэффициенты при должны быть равны, то есть
Если то точки совпадают, но у нас две разные прямые. Тогда
откуда
Тогда
Решая последнее квадратное относительно получаем, что
Тогда
Ошибка.
Попробуйте повторить позже
Решить неравенство
Источники:
Подсказка 1
Видим корни - про что сразу думаем?
Подсказка 2
Про ОДЗ! Но на наше счастье это просто x ∈ ℝ. Что стараемся делать в неравенстве с корнями?
Подсказка 3
Поскорее избавляемся от них :) То есть возводим обе части в квадрат, но всегда ли мы можем это делать?
Подсказка 4
Возводить в квадрат можем только если в левой и правой части стоят выражения одного знака (другие случаи нужно отдельно рассматривать). То есть можно одно из слагаемых перенести в другую часть, чтобы знаки всегда одинаковые были
Подсказка 5
А после этого можно просто рассмотреть случаи раскрытия модуля и решить получающиеся неравенства при помощи напрашивающейся замены. Не забудьте сделать обратную замену и учесть ОДЗ!
Так как под корнями стоят выражения, которые при любых больше нуля, то ОДЗ эта вся вещественная ось. Перенесем слагаемое с
минусом в левую часть и сделаем преобразования.
Возведем в квадрат, в левой и правой части стоят положительные числа
Рассмотрим случай, когда тогда:
Теперь рассмотрим случай, когда
Сделаем заммену
Возведем в квадрат
Решая это квадратное уравнение, получим, что Делая обратную замену, получаем, что
Так как то итоговый ответ
Ошибка.
Попробуйте повторить позже
Внутри параллелограмма взята точка
так, что треугольник
равносторонний. Известно, что расстояния от точки
до
прямых
и
равны соответственно
и
Найти периметр параллелограмма.
Подсказка 1
Давайте обозначим за a угол MNP, а сторону равностороннего треугольника за x. Какие углы и отрезки можно посчитать через них?
Подсказка 2
Мы можем посчитать расстояния от точки P до KL и MN через x и угол a! Тогда у нас получится тригонометрическое уравнение, которое нужно решить.
Подсказка 3
6sin(60-a) = 10sin(a)! Чему равен a? Как выразить через него x?
Подсказка 4
Отлично, теперь мы знаем, чему равен x! Нам известны обе высоты параллелограмма. Какую характеристику у ABCD можно через них выразить?
Подсказка 5
Попробуем найти площадь ABCD двумя способами! Тогда мы сможем отыскать его стороны, а затем найти и периметр ;)
Пусть — расстояния от точки
до прямых
и
соответственно,
и сторона
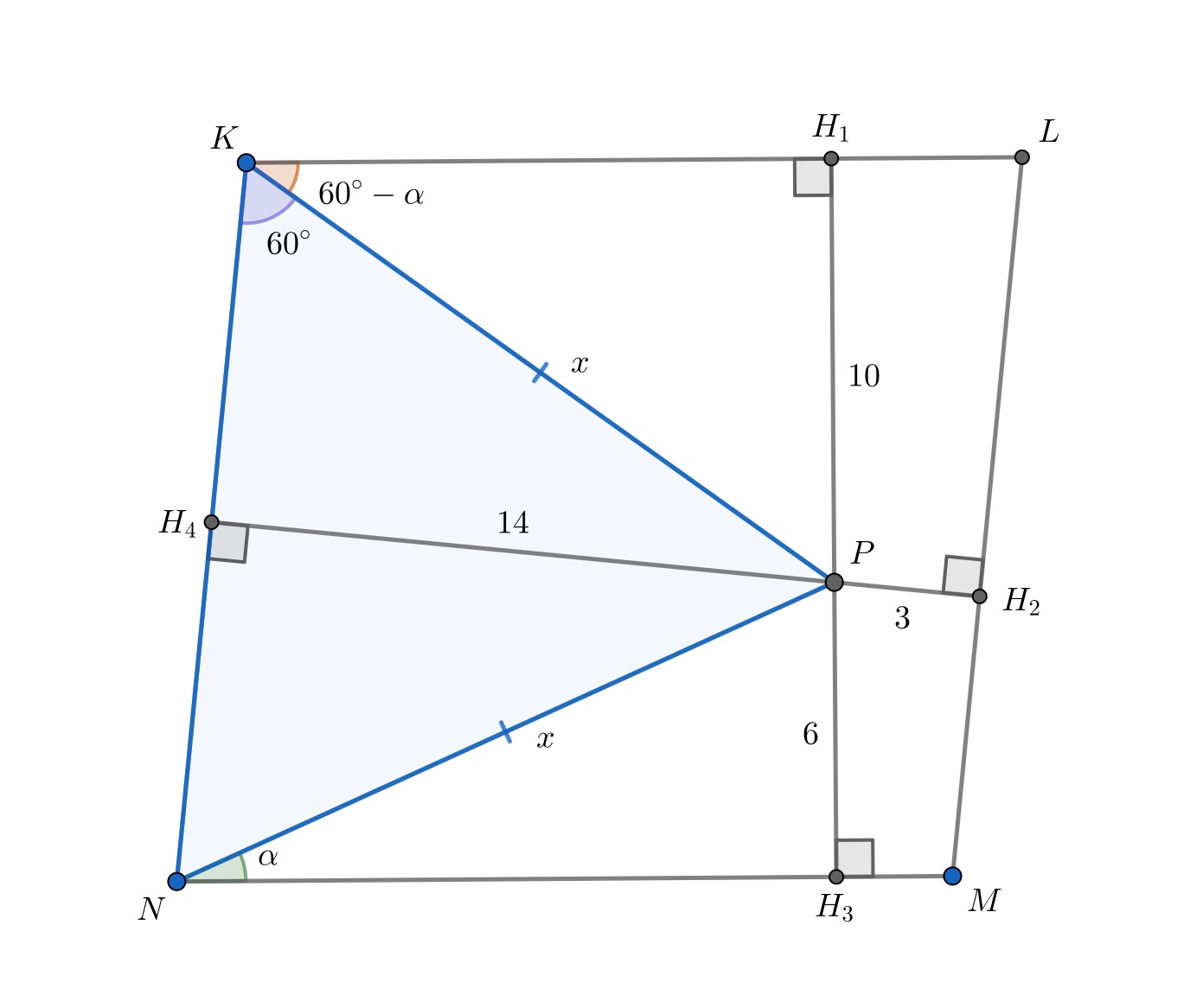
Тогда, так как — равносторонний, а
— параллелограмм, то
Из прямоугольных и
имеем:
То есть:
По формуле синуса разности:
Подставим в изначальное и получим:
Тогда выразим и
Можем теперь выразить
Тогда расстояние до из равностороннего
Тогда
Из того, что — параллелограмм, то по формуле площади:
Так как
Тогда можем посчитать периметр:
Ошибка.
Попробуйте повторить позже
Высоты равнобедренного остроугольного треугольника , в котором
, пересекаются в точке
. Найти площадь
треугольника
, если
, а длина высоты
равна 8.
Источники:
Подсказка 1
Нам даны отрезки AO и OD. Что можно найти с помощью них? Заметьте, что на картинке есть равные и углы...
Подсказка 2
Подобие треугольников! Как с помощью него найти отношение отрезков на сторонах треугольника? Нам нужно получить треугольник, который будет подобен AOH. Таких немало, главное увидеть те, что нам нужны.
Подсказка 3
Опустим перпендикуляр из D на BH! Хочется найти хотя бы одну сторону треугольника…быть может, нужно составить какое-нибудь уравнение? Что мы можем сказать про треугольники, содержащие сторону AB?
Подсказка 4
Рассмотрите треугольник ABD. Составив уравнение на его стороны (с помощью подобия), найдём их. Остаётся лишь найти основание треугольника!
Пусть точка — середина
точка
— проекция
на
Треугольники и
подобны, следовательно,
откуда
![]()
Треугольники и
подобны, следовательно,
откуда Треугольник
— прямоугольный, тогда
Значит, Треугольник
— прямоугольный, тогда:
Таким образом, Тогда площадь треугольника
равна:
Ошибка.
Попробуйте повторить позже
Числа и
являются решениями системы уравнений
где — параметр. Какое наименьшее значение принимает выражение
? При каком
это происходит?
Подсказка 1
В одном уравнении коэффициент а при x, в другом — при y. Это может намекать на некоторое преобразование системы, которое может связать x и y.
Подсказка 2
Сложите два уравнения и разложите части на множители. Что можно сказать о y и x?
Подсказка 3
Получилось, что y = 5 - x. Тогда мы можем найти x через a.
Подсказка 4
Итак, теперь у нас и y, и x выражены в виде дробей с a, и нам нужно минимизировать их сумму квадратов. А чему она равна?
Подсказка 5
Сумма квадратов есть (13a² + 20a + 25)/(a+1)². Как мы умеем искать минимумы у выражений?
Подсказка 6
Будем искать минимум через производную!
Сложим уравнения системы и вынесем общие множители, получим
_________________________________________________________________________________________________________________________________________________________________________________
Пусть тогда
подставим это во второе уравнение системы
______________________________________________________________________________________________________________________________________________________
Пусть тогда
Следовательно,
В итоге выражение, которое нужно минимизировать, примет вид
Исследуем его с помощью производной
Посмотрев на порядок смены знака производной с минуса на плюс при переходе через эту точку, можно сказать, что это точка минимума.
В этой точке выражение равно
Проверим, что выражение не принимает значения меньше при Для этого выделим целую часть
Так как то
тогда
То есть выражение не принимает значения, которые не больше 13, на промежутке
______________________________________________________________________________________________________________________________________________________
Пусть тогда исходная система примет вид
Видно, что система не имеет решений.
_________________________________________________________________________________________________________________________________________________________________________________
Пусть тогда исходная система примет вид
Видно, что система равносильна уравнению
Тогда выражение примет вид
Наименьшее значение парабола с ветвями вверх принимает в вершине, в данном случае наименьшее значение достигается при и
равно
______________________________________________________________________________________________________________________________________________________
Так как то в итоге наименьшее значение выражения
для заданной в условии системы равно 2, достигается оно при
при
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике из точки
расположенной в середине катета
опущен перпендикуляр
на гипотенузу
Найти углы треугольника
если
и
Подсказка 1
Сразу обозначим EL за x, EB за y. Можно ли посчитать другие отрезки? Обратите внимание на то, что на рисунке немало прямоугольных треугольников ;)
Подсказка 2
Воспользуемся теоремой Пифагора для треугольников ELB, ACE, ALE. В каком треугольнике мы знаем все стороны?)
Подсказка 3
Мы можем выразить через x и y все стороны треугольника ABC! Теперь мы можем выразить y через x ;)
Подсказка 4
Обратите внимание на то, что у нас два способа выразить y через x, не противоречит ли кто условию? А как будем считать углы?
Подсказка 5
Углы будем считать при помощи тригонометрических функций!
Пусть Тогда
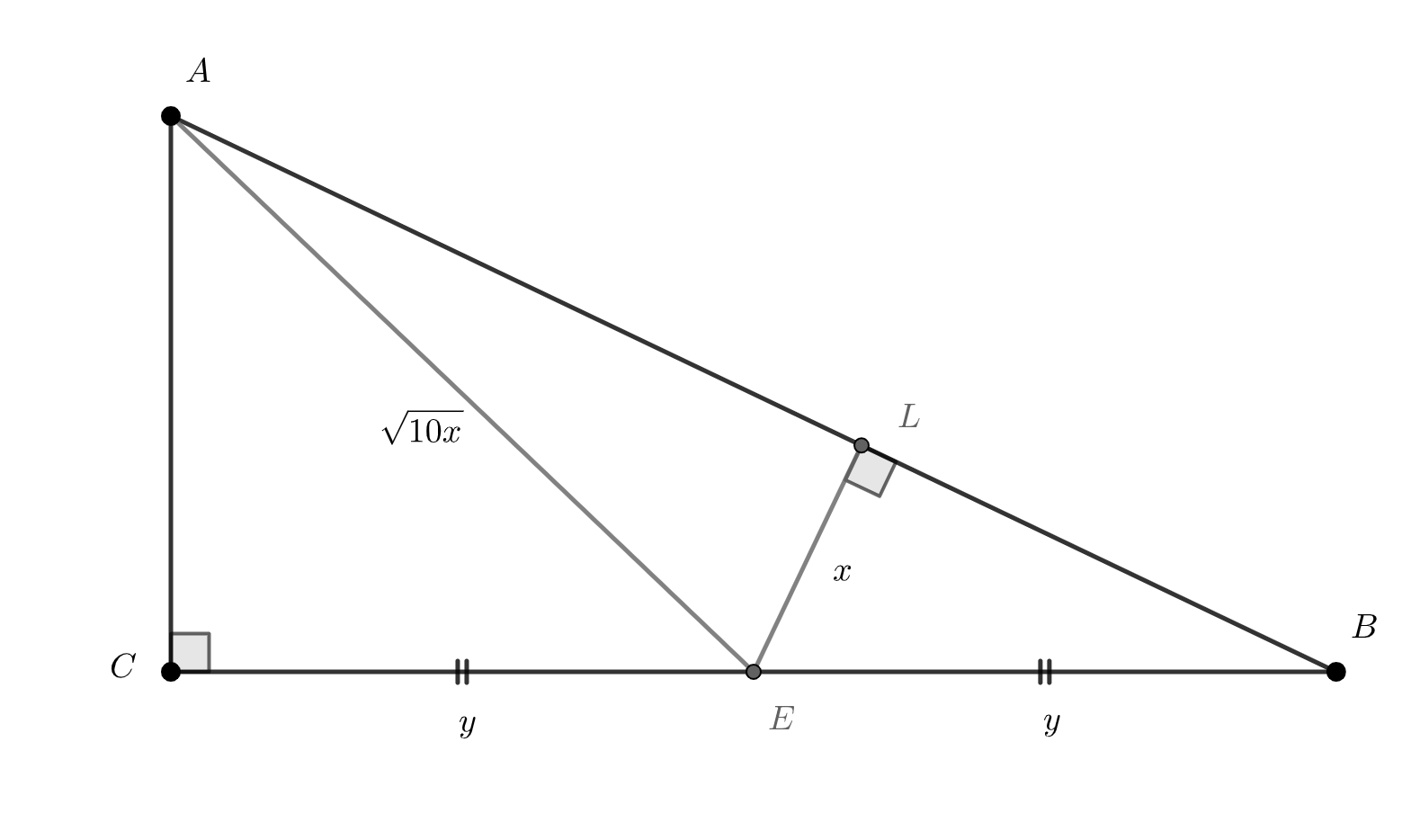
По теореме Пифагора для треугольника
По теореме Пифагора для треугольника
По теореме Пифагора для треугольника
Наконец, по теореме Пифагора для треугольника
Рассмотрим последнее выражение как квадратное уравнение относительно и найдём его корни. Получается, что:
Если то
откуда
то есть треугольники
и
— равнобедренные, что
противоречит условию о том, что
Остаётся верным, что
то есть
Заметим, что при этом
откуда
Итак,



