Окружность, описанная около многоугольника (страница 3)
Готовиться с нами - ЛЕГКО!

Окружность называется описанной около выпуклого многоугольника, если все вершины этого многоугольника лежат на окружности.
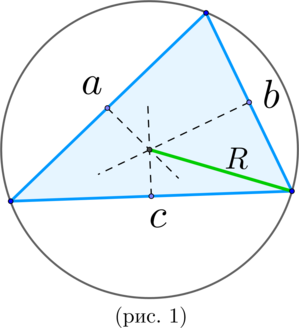
\(\blacktriangleright\) Около любого треугольника можно описать окружность. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника (рис. 1).
Для вписанного треугольника верна формула \[\dfrac{a}{\sin\alpha}=2R,\] где \(\alpha\) – угол треугольника, лежащий против стороны \(a\).
Площадь вписанного треугольника вычисляется по формуле
\[\Large{S_{\triangle}=\dfrac{abc}{4R}}\]
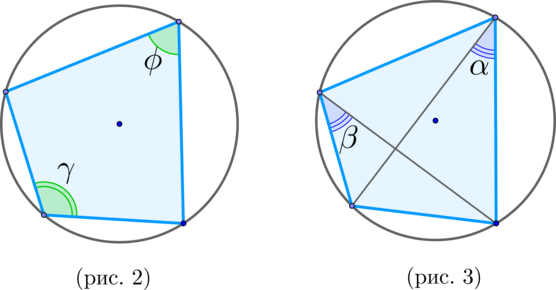
\(\blacktriangleright\) Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна \(\large{\angle\phi + \angle\gamma=180^\circ}\).
И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна \(\large{\angle\phi +
\angle\gamma=180^\circ}\), то около него можно описать окружность. (рис. 2)
\(\blacktriangleright\) Около выпуклого четырехугольника описана окружность \(\Leftrightarrow\) \(\large{\angle \alpha =\angle
\beta}\). (рис. 3)
Площадь вписанного четырехугольника вычисляется по формуле
\[{\large{S_{\text{впис.4-к}}=\sqrt{(p-a)(p-b)(p-c)(p-d)},}}\]
где \(a,b,c,d\) – его стороны, \(p=\frac12(a+b+c+d)\) – полупериметр.
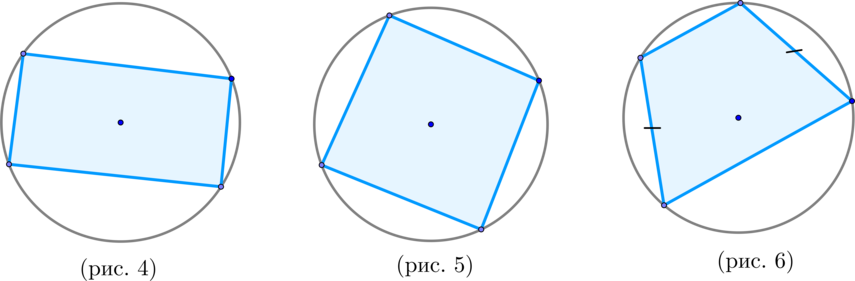
\(\blacktriangleright\) Если около параллелограмма описана окружность, то он – прямоугольник (рис. 4).
\(\blacktriangleright\) Если около ромба описана окружность, то он – квадрат (рис. 5).
\(\blacktriangleright\) Если около трапеции описана окружность, то она равнобедренная.
И наоборот: около равнобедренной (и только равнобедренной) трапеции можно описать окружность (рис. 6).
Два угла вписанного в окружность четырехугольника равны \(82^\circ\) и \(58^\circ\). Найдите больший из оставшихся углов. Ответ дайте в градусах.
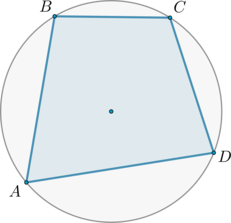
Так как четырехугольник вписан в окружность, то сумма его противоположных углов равна \(180^\circ\). Так как \(82^\circ+58^\circ\ne 180^\circ\), то нам даны градусные меры не противоположных углов. Следовательно, нам даны градусные меры односторонних углов. Допустим \(\angle A=58^\circ\), \(\angle D=82^\circ\). Тогда наибольшим из оставшихся углов будет \(\angle C=180^\circ-\angle A=180^\circ-58^\circ=122^\circ\).
Угол \(A\) четырехугольника \(ABCD\), вписанного в окружность, равен \(58^\circ\). Найдите угол \(C\) этого четырехугольника. Ответ дайте в градусах.

Так как четырехугольник вписан в окружность, то сумма противоположных его углов равна \(180^\circ\). Следовательно, \(\angle A+\angle C=180^\circ\), откуда \(\angle C=180^\circ-58^\circ=122^\circ\).
Около треугольника \(ABC\) описана окружность с центром в точке \(O\). \(\angle BAO+\angle CBO=50^\circ\). Найдите \(\angle ACO\). Ответ дайте в градусах.
Рассмотрим картинку: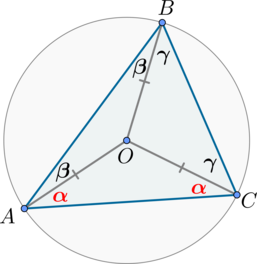
Т.к. треугольники \(AOB\), \(BOC\), \(COA\) – равнобедренные, то \(\angle
OBA=\angle OAB=\beta\), \(\angle OCB=\angle OBC=\gamma\), \(\angle
OCA=\angle
OAC=\alpha\).
Значит, \(\beta+\gamma=50^\circ\).
Т.к. сумма углов треугольника \(ABC\) равна \(180^\circ\), то \[(\beta+\alpha)+(\alpha+\gamma)+(\gamma+\beta)=180^\circ \quad \Rightarrow \quad 2\alpha=180^\circ-2(\beta+\gamma)=80^\circ \quad \Rightarrow \quad \alpha=40^\circ.\]
Около треугольника \(ABC\) описана окружность с центром в точке \(O\). \(\angle BAO=15^\circ, \angle CBO=40^\circ\). Найдите \( \angle ACO\). Ответ дайте в градусах.
Рассмотрим картинку: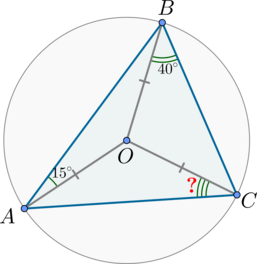
Т.к. треугольники \(AOB\), \(BOC\), \(COA\) – равнобедренные, то \(\angle OBA=15^\circ, \angle OCB=40^\circ\), \(\angle OCA=\angle OAC=\alpha\).
Т.к. сумма углов треугольника \(ABC\) равна \(180^\circ\), то \[(15^\circ+\alpha)+(\alpha+40^\circ)+(40^\circ+15^\circ)=180^\circ \quad \Rightarrow \quad 2\alpha=180^\circ-2(15^\circ+40^\circ)=70^\circ \quad \Rightarrow \quad \alpha=35^\circ.\]
Около треугольника \(ABC\) описана окружность с центром в точке \(O\). \(\angle BAO=20^\circ, \angle BCO=30^\circ\). Найдите \( \angle AOC\). Ответ дайте в градусах.
Рассмотрим картинку: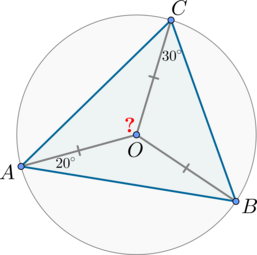
Т.к. треугольники \(AOB\), \(BOC\) – равнобедренные, то \(\angle OBA=\angle OAB=20^\circ\), \(\angle OBC=\angle OCB=30^\circ\). Следовательно, \(\angle B=20^\circ+30^\circ=50^\circ\).
Т.к. \(\angle AOC\) – центральный угол, опирающийся на ту же дугу \(AC\), что и вписанный \(\angle B\), то \(\angle AOC=2\angle B=100^\circ\).
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен \(108^\circ\). Найдите число вершин многоугольника.
1 способ.
Рассмотрим чертеж:
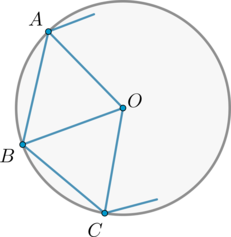
Пусть \(O\) – центр окружности, \(A, B, C\) – три последовательные вершины правильного многоугольника. Тогда \(\angle ABC=108^\circ\).
Заметим, что правильный многоугольник не может иметь 3 или 4 вершины, так как в этом случае это будет правильный треугольник или квадрат, а у этих фигур угол между соседними сторонами равен \(60^\circ\) и \(90^\circ\) соответственно.
Проведем \(OA, OB, OC\) – радиусы. Так как \(AB=BC\), то \(\triangle
AOB=\triangle BOC\). К тому же эти треугольники равнобедренные (\(AB\) и \(BC\) их основания), следовательно, \(\angle ABO=\angle CBO=0,5\cdot
108^\circ=54^\circ\). Отсюда \(\angle AOB=180^\circ-2\cdot
54^\circ=72^\circ\).
Значит, дуга \(AB\) равна \(72^\circ\). Так как равные хорды стягивают равные дуги, а все стороны многоугольника равны (он правильный), то \(n\) вершин многоугольника разбивают окружность на \(n\) дуг, градусные меры которых равны \(72^\circ\). То есть \(72^\circ\cdot n=360^\circ\), откуда \(n=5\).
2 способ.
Так как многоугольник правильный, его угол равен \(108^\circ\), а сумма всех углов правильного многоугольника равна \(180^\circ\cdot
(n-2)\), где \(n\) – число вершин, то \[108^\circ\cdot n=180^\circ(n-2)\quad\Rightarrow\quad
n=5\] В таком случае информацию о том, что многоугольник вписан в окружность, мы не использовали.
Во вписанном четырехугольнике \(LEGO\) стороны \(LE\) и \(GO\) равны. Найдите сумму углов \(\angle L\) и \(\angle E\). Ответ дайте в градусах.
Рассмотрим картинку: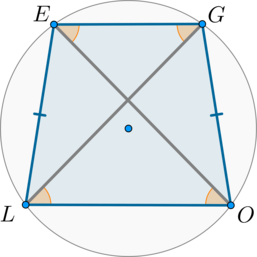
Т.к. хорды \(LE\) и \(GO\) равны, то равны дуги \(\buildrel\smile\over{LE}\) и \(\buildrel\smile\over{GO}\). Следовательно, вписанные углы, опирающиеся на эти дуги, будут тоже равны:
\[\angle LOE=\angle LGE=\angle OLG=\angle OEG\]
Таким образом, \(LEGO\) – трапеция (\(\angle LOE=\angle OEG\) – накрест лежащие при прямых \(EG\) и \(LO\) и секущей \(EO\)). Значит, \(\angle L+\angle E=180^\circ\) как сумма односторонних углов при параллельных прямых.



