Окружность, описанная около многоугольника (страница 5)
Готовиться с нами - ЛЕГКО!

Окружность называется описанной около выпуклого многоугольника, если все вершины этого многоугольника лежат на окружности.
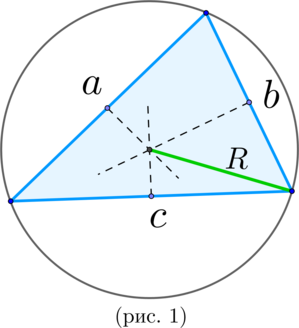
\(\blacktriangleright\) Около любого треугольника можно описать окружность. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника (рис. 1).
Для вписанного треугольника верна формула \[\dfrac{a}{\sin\alpha}=2R,\] где \(\alpha\) – угол треугольника, лежащий против стороны \(a\).
Площадь вписанного треугольника вычисляется по формуле
\[\Large{S_{\triangle}=\dfrac{abc}{4R}}\]
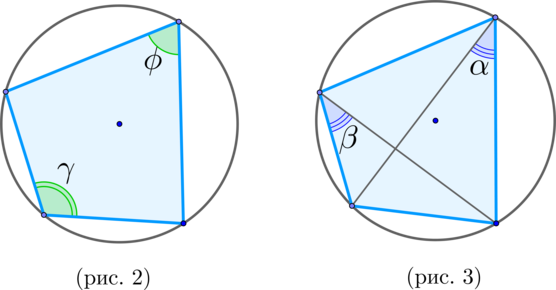
\(\blacktriangleright\) Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна \(\large{\angle\phi + \angle\gamma=180^\circ}\).
И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна \(\large{\angle\phi +
\angle\gamma=180^\circ}\), то около него можно описать окружность. (рис. 2)
\(\blacktriangleright\) Около выпуклого четырехугольника описана окружность \(\Leftrightarrow\) \(\large{\angle \alpha =\angle
\beta}\). (рис. 3)
Площадь вписанного четырехугольника вычисляется по формуле
\[{\large{S_{\text{впис.4-к}}=\sqrt{(p-a)(p-b)(p-c)(p-d)},}}\]
где \(a,b,c,d\) – его стороны, \(p=\frac12(a+b+c+d)\) – полупериметр.
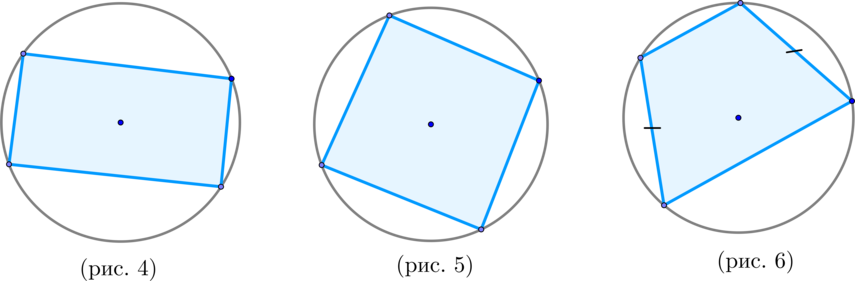
\(\blacktriangleright\) Если около параллелограмма описана окружность, то он – прямоугольник (рис. 4).
\(\blacktriangleright\) Если около ромба описана окружность, то он – квадрат (рис. 5).
\(\blacktriangleright\) Если около трапеции описана окружность, то она равнобедренная.
И наоборот: около равнобедренной (и только равнобедренной) трапеции можно описать окружность (рис. 6).
Около пятиугольника \(ABCDE\) описана окружность, причем \(AB=BC=CD=DE=4\sqrt3\), \(\angle A=90^\circ\). Найдите \(AE\).
Рассмотрим картинку: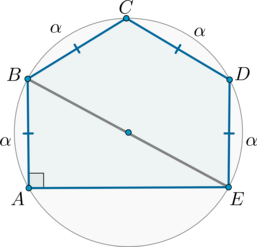
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:
\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]
Следовательно, \(\angle A=90^\circ=\frac32\alpha\), откуда \(\alpha=60^\circ\).
Значит, вписанный \(\angle AEB=\frac12\alpha=30^\circ\). Следовательно, из прямоугольного треугольника \(AEB\)
\[\mathrm{tg}\,30^\circ=\dfrac{AB}{AE} \quad \Rightarrow \quad AE=12.\]
Около пятиугольника \(ABCDE\) описана окружность, причем \(AB=BC=CD=DE\), \(AE=6\sqrt3\), \(\angle A=45^\circ\). Найдите радиус описанной около этого пятиугольника окружности.
Рассмотрим картинку: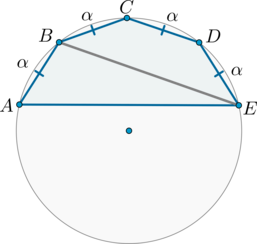
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:
\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]
Следовательно, \(\angle A=45^\circ=\frac32\alpha\), откуда \(\alpha=30^\circ\).
Значит, вписанный \[\angle ABE=\frac12\buildrel\smile\over{AE}= \frac12\left(360^\circ-4\alpha\right)=120^\circ\]
Тогда, т.к. \(\triangle ABE\) – вписанный, то \(\dfrac{AE}{\sin \angle B}=2R\), где \(R\) – радиус данной окружности. Следовательно:
\[\dfrac{AE}{\sin \angle B}=2R \quad \Rightarrow \quad R=6.\]
Около пятиугольника \(ABCDE\) описана окружность, причем \(AB=BC=CD=DE\), \(AE=8\sqrt3\), \(\angle A=45^\circ\). Найдите высоту треугольника \(ACE\), опущенную из вершины угла \(C\).
Рассмотрим картинку: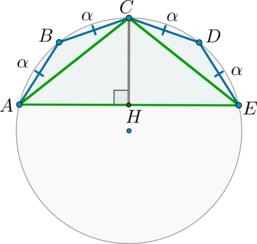
Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:
\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]
Следовательно, \(\angle A=45^\circ=\frac32\alpha\), откуда \(\alpha=30^\circ\).
Тогда \(\angle CAE=\frac12\cdot 2\alpha=30^\circ\).
Заметим, что \(\triangle ACE\) – равнобедренный (\(\angle A=\angle E=\alpha\)), следовательно, \(CH\) – высота и медиана, то есть \(AH=\frac12\cdot AE=4\sqrt3\). Значит:
\[\mathrm{tg}\,30^\circ=\dfrac{CH}{AH} \quad \Rightarrow \quad CH=4.\]
Около пятиугольника \(ABCDE\) описана окружность, причем \(AB=BC=CD=DE\). Радиус этой окружности равен \(5\). Найдите радиус окружности, описанной около треугольника \(BQD\), где \(Q\) – точка пересечения отрезков \(AD\) и \(BE\).
Рассмотрим картинку: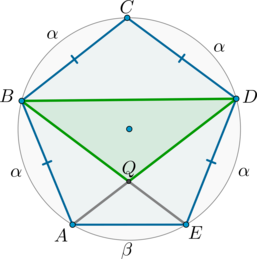
1) Т.к. равные хорды стягивают равные дуги, то меньшие полуокружности дуги \(\buildrel\smile\over{AB}\), \(\buildrel\smile\over{BC}\), \(\buildrel\smile\over{CD}\), \(\buildrel\smile\over{DE}\) равны:
\[\buildrel\smile\over{AB}=\buildrel\smile\over{BC}= \buildrel\smile\over{CD}=\buildrel\smile\over{DE}=\alpha.\]
Пусть также \(\buildrel\smile\over{EA}=\beta\).
2) \(\angle CBE=\frac12(\alpha+\alpha)=\alpha\), \(\angle BCD=\frac12(\alpha+\beta+\alpha)=\alpha+\frac12\beta\). Следовательно, \(\angle CBE+\angle BCD=2\alpha+\frac12\beta\).
Заметим, что градусная мера всей окружности равна \(360^\circ\), следовательно, \(4\alpha+\beta=360^\circ\), откуда \(2\alpha+\frac12\beta=180^\circ\). Таким образом, \(\angle CBE\) и \(\angle BCD\) – односторонние углы при прямых \(CD\) и \(BE\) и секущей \(BC\). Следовательно, \(CD\parallel BE\).
Аналогично доказывается, что \(AD\parallel BC\).
3) Значит, \(BCDQ\) – параллелограмм (\(BQ\parallel CD, BC\parallel QD\)). А в параллелограмме противоположные стороны равны, следовательно, \(BQ=CD=BC=DQ\). То есть \(BCDQ\) – ромб.
4) Таким образом, \(\triangle BCD=\triangle BQD\). Значит, и радиусы описанных около этих треугольников окружностей равны. Но радиус описанной около \(\triangle BCD\) окружности равен радиусу описанной около пятиугольника \(ABCDE\) окружности. Следовательно, ответ \(5\).
Стоугольник \(A_1...A_{100}\) вписан в окружность. Найдите \(\angle A_1 + \angle A_3 + \angle A_5 + ... + \angle A_{99}\). Ответ дайте в градусах.
\(\angle A_1\), \(\angle A_3\), ..., \(\angle A_{99}\) – вписанные, тогда \(\angle A_1 = 0,5\cdot\smile A_2...A_{100}\), ..., \(\angle A_{99} = 0,5\cdot\smile A_{100}A_1...A_{98}\).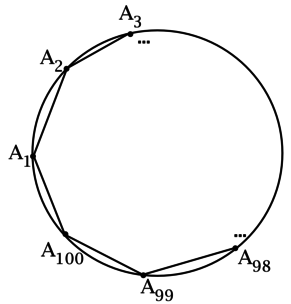
Назовём меньшую дугу \(\smile A_1A_2\) малой. Аналогично назовём меньшие дуги \(\smile A_2A_3\), ..., \(\smile A_{100}A_1\) малыми. Каждую из дуг \(\smile A_2...A_{100}\), ..., \(\smile
A_{100}A_1...A_{98}\) можно разложить в сумму малых дуг.
\(\angle A_1 + \angle A_3 + \angle A_5 + ... + \angle A_{99} = 0,5\cdot\)(сумму некоторых малых дуг).
Остаётся понять, сколько раз в данную сумму войдёт каждая малая дуга.
Например, \(\smile A_1A_2\) войдёт \(50 - 1 = 49\) раз (среди \(50\) слагаемых \(\smile A_2...A_{100}\), ..., \(\smile A_{100}A_1...A_{98}\) она не входит только в \(\smile A_2...A_{100}\)).
Аналогично любая дуга войдёт в данную сумму \(49\) раз, следовательно, \[\angle A_1 + \angle A_3 + \angle A_5 + ... + \angle A_{99} = 0,5\cdot 49l,\] где \(l\) – градусная мера окружности.
Так как \(l = 360^\circ\), то \[\angle A_1 + \angle A_3 + \angle A_5 + ... + \angle A_{99} = \left(\dfrac{100}{2} - 1\right)\cdot 180^\circ = 8820^\circ.\]
Во вписанном четырехугольнике \(ABCD\) противоположные стороны попарно равны \(5\) и \(12\). Найдите радиус описанной около этого четырехугольника окружности.
Рассмотрим картинку: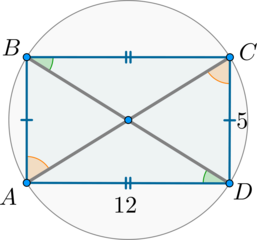
Т.к. хорды \(AB\) и \(CD\) равны, то равны дуги \(\buildrel\smile\over{AB}\) и \(\buildrel\smile\over{CD}\). Следовательно, вписанные углы, опирающиеся на эти дуги, будут тоже равны:
\[\angle ADB=\angle ACB=\angle DAC=\angle DBC\]
Таким образом, \(\angle ADB=\angle DBC\) – накрест лежащие при прямых \(AD\) и \(BC\) и секущей \(BD\), следовательно, \(AD\parallel BC\).
Аналогичным образом доказывается, что \(AB\parallel CD\).
Таким образом, \(ABCD\) – параллелограмм. Т.к. он вписанный, то это – прямоугольник.
В прямоугольнике центр описанной окружности лежит на пересечении диагоналей. Следовательно, по теореме Пифагора \(AC=\sqrt{5^2+12^2}=13\), а \(R=\frac12AC=6,5\).
Замечание.
Можно было доказать, что \(ABCD\) – прямоугольник, другим способом:
\(\triangle ABD=\triangle CBD\) по трем сторонам. Следовательно, \(\angle A=\angle C\). Но т.к. четырехугольник вписанный, то сумма противоположных углов равна \(180^\circ\), следовательно, \(\angle A+\angle C=180^\circ\). Отсюда следует, что \(\angle A=\angle C=90^\circ\). Аналогично \(\angle B=\angle D=90^\circ\). По признаку четырехугольник, у которого все углы прямые, является прямоугольником.
Радиус описанной около четырехугольника \(ABCD\) окружности равен \(3\). Найдите площадь этого четырехугольника, если известно, что все его стороны равны.
Рассмотрим картинку: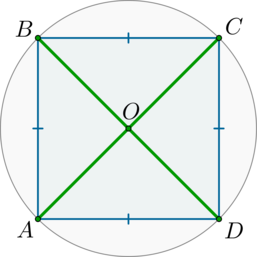
Докажем, что данный четырехугольник является квадратом.
Т.к. хорды \(AB\) и \(CD\) равны, то равны дуги \(\buildrel\smile\over{AB}\) и \(\buildrel\smile\over{CD}\). Следовательно, вписанные углы, опирающиеся на эти дуги, будут тоже равны:
\[\angle ADB=\angle ACB=\angle DAC=\angle DBC\]
Таким образом, \(\angle ADB=\angle DBC\) – накрест лежащие при прямых \(AD\) и \(BC\) и секущей \(BD\), следовательно, \(AD\parallel BC\).
Аналогичным образом доказывается, что \(AB\parallel CD\).
Таким образом, \(ABCD\) – параллелограмм. Т.к. он вписанный, то это – прямоугольник. Т.к. все его стороны равны, то это квадрат.
В квадрате центр описанной окружности лежит на пересечении диагоналей, следовательно, \(AC=2R=6\). По свойству квадрата \(AD=AC\div \sqrt2=3\sqrt2\). Следовательно, площадь
\[S_{ABCD}=AD^2=(3\sqrt2)^2=18.\]
Замечание.
Можно было доказать, что \(ABCD\) – квадрат, другим способом:
\(\triangle ABD=\triangle CBD\) по трем сторонам. Следовательно, \(\angle A=\angle C\). Но т.к. четырехугольник вписанный, то сумма противоположных углов равна \(180^\circ\), следовательно, \(\angle A+\angle C=180^\circ\). Отсюда следует, что \(\angle A=\angle C=90^\circ\). Аналогично \(\angle B=\angle D=90^\circ\). По признаку четырехугольник, у которого все углы прямые, является прямоугольником. Но т.к. у него еще и все стороны равны, то это квадрат.



