Окружность. Основные теоремы, связанные с окружностями

Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.

 

Теорема 1.

1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.

 

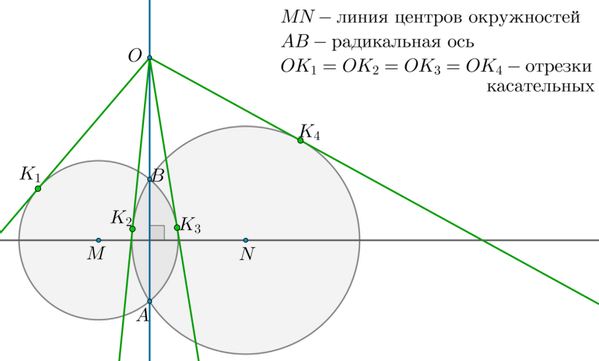
Доказательство:

1) Рассмотрим $\triangle BMN$ и $\triangle AMN$: они равны по трем сторонам ($BM=AM=R_1, BN=AN=R_2$ — радиусы первой и второй окружностей соответственно). Таким образом, $\angle BNM=\angle ANM$, следовательно, $MN$ — биссектриса в равнобедренном $\triangle ANB$, следовательно, $MN\perp AB$.

 

2) Отметим произвольную точку $O$ на радикальной оси и проведем касательные $OK_1, OK_3$ к первой окружности и $OK_2, OK_4$ ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то $OK_1^2=OK_2^2=OK_3^2=OK_4^2=OB\cdot OA$.

 

Теорема 2.

Пусть две окружности с центрами $M$ и $N$ касаются внешним образом в точке $A$. Две общие касательные (внутренняя и внешняя) $a$ и $b$ этих окружностей пересекаются в точке $B$. Точки касания — точки $A, K_1, K_2$ (как показано на рисунке). Тогда $$(1) \ {\large{K_1B=AB=K_2B}}$$ $$(2) \ {\large{\angle K_1AK_2=90^\circ}}$$

 

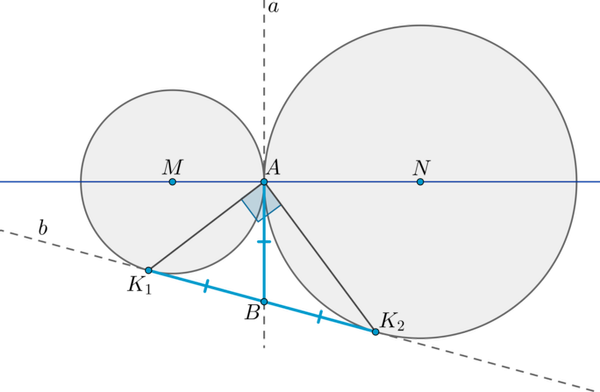
Доказательство:

1) Т.к. $BA$ и $BK_1$ — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: $BA=BK_1$. Аналогично, $BA=BK_2$. Таким образом, $BA=BK_1=BK_2$.

 

2) Значит, $BA$ — медиана в $\triangle K_1AK_2$, равная половине стороны, к которой она проведена. Значит, $\angle A=90^\circ$.

 

Теорема 3.

Пусть две окружности касаются внешним образом в точке $A$. Через точку $A$ проведены две прямые $B_1B_2$ и $C_1C_2$, пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: $$(1) \ {\large{\triangle AB_1C_1 \sim \triangle AB_2C_2}}$$ $$(2) \ {\large{B_1C_1\parallel B_2C_2}}$$

 

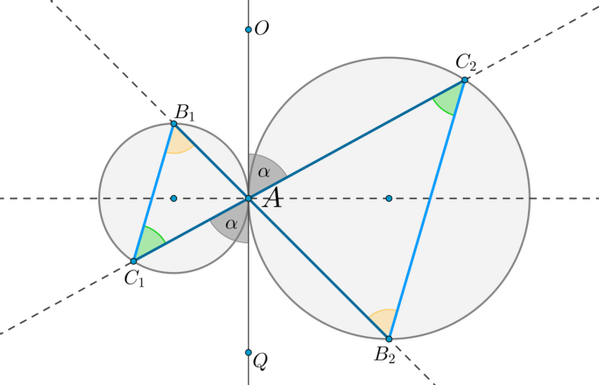
Доказательство:

1) Проведем через точку $A$ общую касательную этих окружностей $OQ$. $\angle OAC_2=\angle QAC_1=\alpha$ как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то $\angle OAC_2=\frac12\buildrel\smile\over{AC_2}$, $\angle QAC_1=\frac12\buildrel\smile\over{AC_1}$. Следовательно, $\buildrel\smile\over{AC_1}=\buildrel\smile\over{AC_2}=2\alpha$. Таким образом, $\angle AB_1C_1=\angle AB_2C_2=\alpha$. Значит, по двум углам $\triangle AB_1C_1\sim \triangle AB_2C_2$.

 

2) Т.к. $\angle AB_1C_1=\angle AB_2C_2$, то прямые $B_1C_1\parallel B_2C_2$ по накрест лежащим углам при секущей $B_1B_2$.

 

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: $$AC\cdot BD=AB\cdot CD+BC\cdot AD$$

Доказательство

Пусть для определенности $\angle ABD<\angle CBD$. Проведем отрезок $BO$ так, чтобы $O$ лежала на $AC$ и $\angle ABD=\angle CBO$:

 

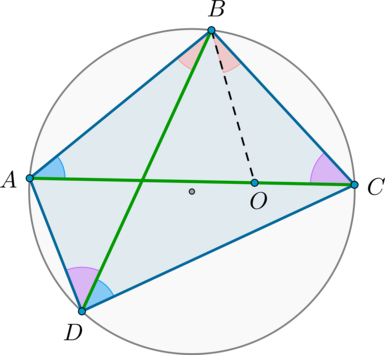
Т.к. $\angle ACB=\angle ADB$ (опираются на одну и ту же дугу), то по двум углам $\triangle OBC\sim \triangle ABD$. Значит: $$\dfrac{OC}{AD}=\dfrac{BC}{BD} \Rightarrow AD\cdot BC=OC\cdot BD\phantom{00000000000} (1)$$

Т.к. $\angle BAC=\angle BDC$ (опираются на одну и ту же дугу), $\angle ABO=\angle CBD$ (состоят из равных по построению (оранжевых) углов и общего угла $\angle DBO$), то по двум углам $\triangle ABO\sim \triangle BDC$. Значит: $$\dfrac{AO}{DC}=\dfrac{AB}{BD} \Rightarrow AB\cdot CD=AO\cdot BD \phantom{00000000000} (2)$$

Сложим равенства $(1)$ и $(2)$: $AD\cdot BC+AB\cdot CD=OC\cdot BD+AO\cdot BD=AC\cdot BD$, чтд.

 

Формула Эйлера:

Пусть $R$ — радиус описанной около треугольника $ABC$ окружности, $r$ — радиус вписанной окружности. Тогда расстояние $d$ между центрами этих окружностей вычисляется по формуле: $${\large{d^2=R^2-2Rr}}$$

 

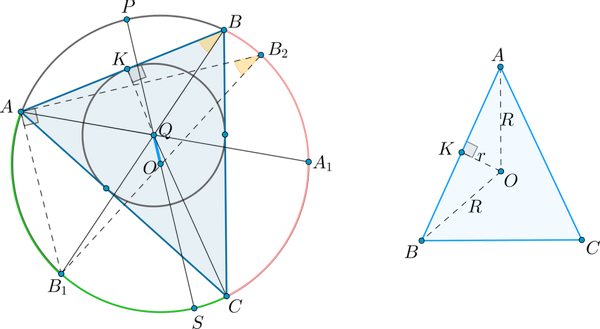
Доказательство:

а) Предположим, что $d\ne 0$. Пусть $O, Q$ — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности $PS$ через точку $Q$. Проведем также биссектрисы углов $\angle A, \angle B$ — $AA_1, BB_1$ соответственно (заметим, что они пересекутся в точке $Q$, т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды $PS$ и $BB_1$ пересекаются, следовательно, отрезки этих хорд равны: $PQ\cdot QS=BQ\cdot QB_1$.

 

Т.к. $OP=OS=R, OQ=d$, то последнее равенство можно переписать в виде $(R-d)(R+d)=BQ\cdot QB_1 \ (*)$.

 

Заметим, что т.к. $AA_1, BB_1$ — биссектрисы, то $\buildrel\smile\over{AB_1}=\buildrel\smile\over{B_1C}=x, \ \buildrel\smile\over{CA_1}=\buildrel\smile\over{A_1B}=y$. Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
$\angle AQB_1=\frac12(x+y)$.

 

С другой стороны, $\angle B_1AA_1=\frac12\big(\buildrel\smile\over{B_1C}+\buildrel\smile\over{CA_1}\big)=\frac12(x+y)$

 

Таким образом, $\angle AQB_1=\angle B_1AA_1$. Следовательно, $\triangle QB_1A$ — равнобедренный и $B_1Q=B_1A$. Значит, равенство $(*)$ можно переписать как:
$R^2-d^2=BQ\cdot AB_1 \ (**)$.

 

Проведем еще один диаметр описанной окружности $B_1B_2$. Тогда $\triangle B_1AB_2$ — прямоугольный ($\angle A$ опирается на диаметр). Пусть также вписанная окружность касается стороны $AB$ в точке $K$. Тогда $\triangle BKQ$ — прямоугольный.
Заметим также, что $\angle KBQ=\angle AB_2B_1$ (т.к. они опираются на одну и ту же дугу).
Значит, $\triangle B_1AB_2\sim \triangle BKQ$ по двум углам, следовательно:

 

$\dfrac{KQ}{AB_1}=\dfrac{BQ}{B_1B_2} \Rightarrow \dfrac{r}{AB_1}=\dfrac{BQ}{2R} \Rightarrow BQ\cdot AB_1=2Rr$.

 

Подставим это в $(**)$ и получим:

$R^2-d^2=2Rr \Rightarrow d^2=R^2-2Rr$.

 

б) Если $d=0$, т.е. центры вписанной и описанной окружностей совпадают, то $AK=BK=\sqrt{R^2-r^2} \Rightarrow AB=2\sqrt{R^2-r^2}$. Аналогично $AC=BC=AB=\sqrt{R^2-r^2}$, т.е. треугольник равносторонний. Следовательно, $\angle A=60^\circ \Rightarrow \angle KAO=30^\circ \Rightarrow r=\frac12R \Rightarrow R=2r$ или $0=R^2-2Rr$ (т.е. в этом случае формула также верна).

 

Теорема о бабочке:

Пусть через середину хорды $AB$ — точку $O$, проведены две хорды $MN$ и $KP$. Пусть $MP\cap AB=X, KN\cap AB=Y$. Тогда $${\large{OX=OY}}$$

 

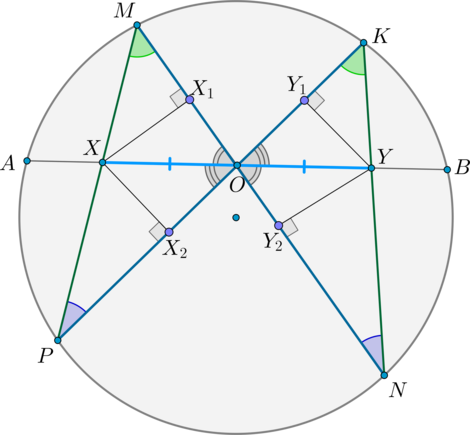
Доказательство:

Проведем перпендикуляры $XX_1, YY_2\perp MN, XX_2, YY_1\perp KP$.
Следующие углы равны, т.к. опираются на одну и ту же дугу: $\angle PMO=\angle NKO, \angle MPO=\angle KNO$.
Следующие углы равны, т.к. вертикальные: $\angle XOX_1=\angle YOY_2, \angle XOX_2=\angle YOY_1$.

 

Следующие прямоугольные треугольники подобны:

 

1) $\triangle XX_1O\sim \triangle YY_2O \Rightarrow \dfrac{XO}{YO}=\dfrac{XX_1}{YY_2}$

 

2) $\triangle XX_2O\sim \triangle YY_1O \Rightarrow \dfrac{XO}{YO}=\dfrac{XX_2}{YY_1}$

 

3) $\triangle MXX_1\sim \triangle KYY_1 \Rightarrow \dfrac{XX_1}{YY_1}=\dfrac{MX}{KY}$

 

4) $\triangle PXX_2\sim \triangle NYY_2 \Rightarrow \dfrac{XX_2}{YY_2}=\dfrac{PX}{NY}$

 

Из 1) и 2) следует, что

 

$\dfrac{XO^2}{YO^2}=\dfrac{XX_1\cdot XX_2}{YY_1\cdot YY_2}$

 

Из 3) и 4) следует, что

 

$\dfrac{XX_1\cdot XX_2}{YY_1\cdot YY_2}=\dfrac{MX\cdot PX}{KY\cdot NY}$

 

Совместив последние два равенства, получим:

 

$\dfrac{XO^2}{YO^2}=\dfrac{MX\cdot PX}{KY\cdot NY}$

 

Заметим, что для пересекающихся хорд $AB$ и $MP$: $AX\cdot XB=MX\cdot PX$. Аналогично $AY\cdot YB=KY\cdot NY$. Значит:

 

$\dfrac{XO^2}{YO^2}==\dfrac{AX\cdot XB}{AY\cdot YB}$

 

Обозначим $OX=x, OY=y, OA=OB=t \Rightarrow$

 

$\dfrac{x^2}{y^2}=\dfrac{(t-x)(t+x)}{(t+y)(t-y)}=\dfrac{t^2-x^2}{t^2-y^2} \Rightarrow x^2t^2-x^2y^2=y^2t^2-x^2y^2 \Rightarrow x^2=y^2 \Rightarrow x=y$.