Окружность: вписанная в многоугольник или угол

Определения

Окружность $S$ вписана в угол $\alpha$, если $S$ касается сторон угла $\alpha$.

 

Окружность $S$ вписана в многоугольник $P$, если $S$ касается всех сторон $P$.

В этом случае многоугольник $P$ называется описанным около окружности.

 

Теорема

Центр вписанной в угол окружности лежит на его биссектрисе.

 

Доказательство

 

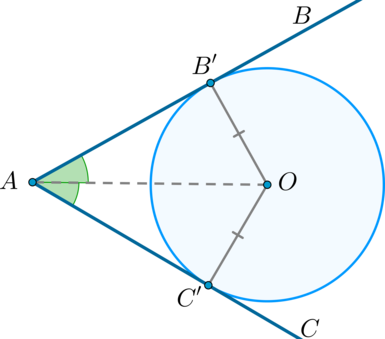
Пусть $O$ – центр некоторой окружности, вписанной в угол $BAC$. Пусть $B'$ – точка касания окружности и $AB$, а $C'$ – точка касания окружности и $AC$, тогда $OB'$ и $OC'$ – радиусы, проведённые в точки касания, следовательно, $OC'\perp AC$, $OB'\perp AB$, $OC' = OB'$.

 

Значит, треугольники $AC'O$ и $AB'O$ – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда $\angle CAO = \angle BAO$, что и требовалось доказать.

 

Теорема

В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.

 

Доказательство

Проведем биссектрисы углов $\angle A$ и $\angle B$. Пусть они пересеклись в точке $O$.

 

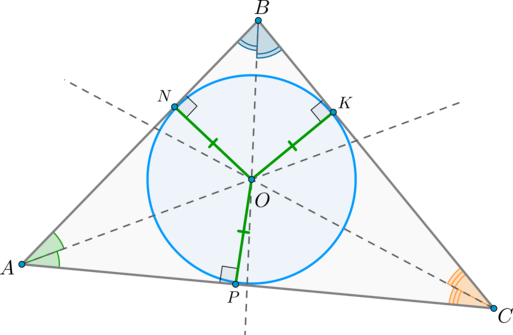
Т.к. $O$ лежит на биссектрисе $\angle A$, то расстояния от точки $O$ до сторон угла равны: $ON=OP$.

 

Т.к. $O$ также лежит на биссектрисе $\angle B$, то $ON=OK$. Таким образом, $OP=OK$, следовательно, точка $O$ равноудалена от сторон угла $\angle C$, следовательно, лежит на его биссектрисе, т.е. $CO$ – биссектриса $\angle C$.

 

Таким образом, точки $N, K, P$ равноудалены от точки $O$, то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.

 

Данная окружность единственна, т.к. если предположить, что существует другая вписанная в $\triangle ABC$ окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.

 

Таким образом, попутно была доказана следующая теорема:

 

Следствие

Биссектрисы треугольника пересекаются в одной точке.

 

Теорема о площади описанного треугольника

Если $a,b,c$ – стороны треугольника, а $r$ – радиус вписанной в него окружности, то площадь треугольника $$S_{\triangle}=p\cdot r$$ где $p=\dfrac{a+b+c}2$ – полупериметр треугольника.

 

Доказательство

 

$S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle AOB}+S_{\triangle BOC}=\frac12OP\cdot AC+\frac12 ON\cdot AB+\frac12 OK\cdot BC$.

 

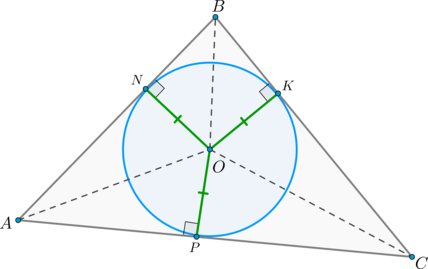
Но $ON=OK=OP=r$ – радиусы вписанной окружности, следовательно,

$$S_{\triangle ABC}=\frac12 r (AC+AB+BC)=p\cdot r$$

Следствие

Если в многоугольник вписана окружность и $r$ – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на $r$: $$S_{\text{опис.мног-к}}=p\cdot r$$

Теорема

В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

 

Доказательство

Необходимость. Докажем, что если в $ABCD$ вписана окружность, то $AB+CD=BC+AD$.

 

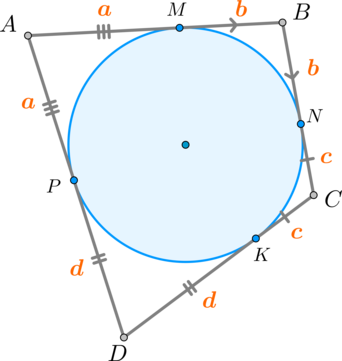
Пусть $M,N,K,P$ – точки касания окружности и сторон четырехугольника. Тогда $AM, AP$ – отрезки касательных к окружности, проведенные из одной точки, следовательно, $AM=AP=a$. Аналогично, $BM=BN=b, \ CN=CK=c, \ DK=DP=d$.

 

Тогда: $AB+CD=a+b+c+d=BC+AD$.

 

Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.

 

Проведем биссектрисы углов $\angle A$ и $\angle B$, пусть они пересекутся в точке $O$. Тогда точка $O$ равноудалена от сторон этих углов, то есть от $AB, BC, AD$. Впишем окружность в $\angle A$ и $\angle B$ с центром в точке $O$. Докажем, что эта окружность будет касаться и стороны $CD$.

 

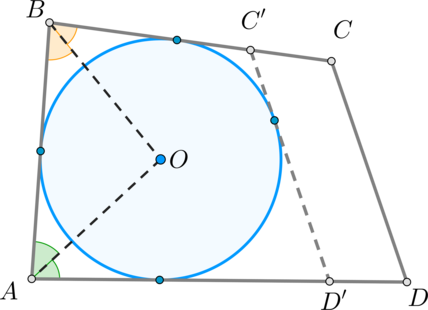
Предположим, что это не так. Тогда $CD$ либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).

 

Проведем касательную прямую $C'D' \parallel CD$ (как показано на рисунке). Тогда $ABC'D'$ – описанный четырехугольник, следовательно, $AB+C'D'=BC'+AD'$.

 

Т.к. $BC'=BC-CC', \ AD'=AD-DD'$, то:

$$AB+C'D'=BC-CC'+AD-DD' \Rightarrow C'D'+CC'+DD'=BC+AD-AB=CD$$

Получили, что в четырехугольнике $C'CDD'$ сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, $CD$ касается окружности.

 

Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.

 

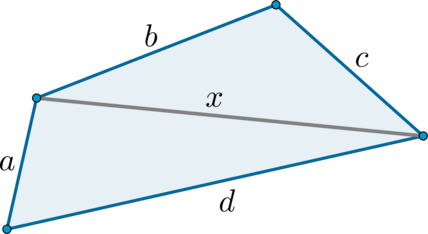
Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то $a+x>d$ и $b+c>x$. Складывая данные неравенства, получим: $a+x+b+c>d+x \Rightarrow a+b+c>d$. Следовательно, сумма любых трех сторон всегда больше четвертой стороны.

 

Теоремы

1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).

 

2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).

 

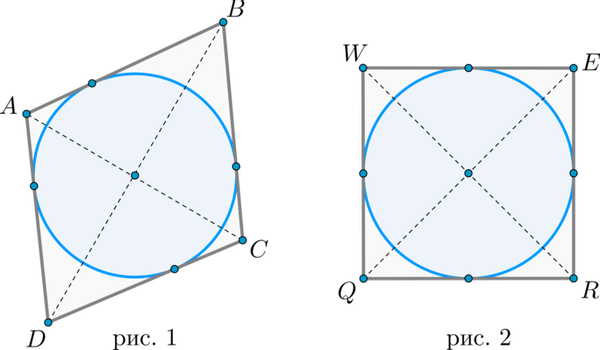
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.

 

Доказательство

1) Рассмотрим параллелограмм $ABCD$, в который вписана окружность. Тогда $AB+CD=BC+AD$. Но в параллелограмме противоположные стороны равны, т.е. $AB=CD, \ BC=AD$. Следовательно, $2AB=2BC$, а значит, $AB=BC=CD=AD$, т.е. это ромб.

 

Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.

 

2) Рассмотрим прямоугольник $QWER$. Т.к. прямоугольник является параллелограммом, то согласно первому пункту $QW=WE=ER=RQ$, т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.

 

Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.