Трапеция

$${\Large{\text{Произвольная трапеция}}}$$

Определения

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

 

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

 

Теоремы: свойства трапеции

 

1) Сумма углов при боковой стороне равна $180^\circ$.

 

2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

 

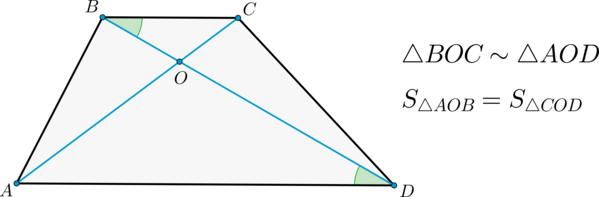
Доказательство

1) Т.к. $AD\parallel BC$, то углы $\angle BAD$ и $\angle ABC$ – односторонние при этих прямых и секущей $AB$, следовательно, $\angle BAD +\angle ABC=180^\circ$.

 

2) Т.к. $AD\parallel BC$ и $BD$ – секущая, то $\angle DBC=\angle BDA$ как накрест лежащие.
Также $\angle BOC=\angle AOD$ как вертикальные.
Следовательно, по двум углам $\triangle BOC \sim \triangle AOD$.

Докажем, что $S_{\triangle AOB}=S_{\triangle COD}$. Пусть $h$ – высота трапеции. Тогда $S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}$. Тогда: $$S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}$$

 

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

 

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

 

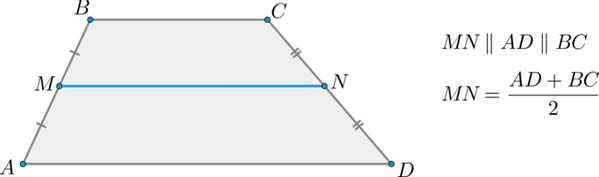
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

 

1) Докажем параллельность.

 

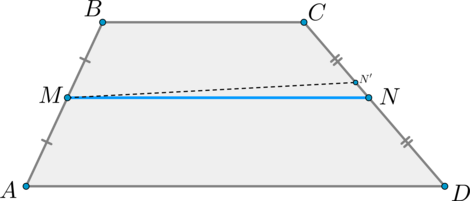
Проведем через точку $M$ прямую $MN'\parallel AD$ ($N'\in CD$). Тогда по теореме Фалеса (т.к. $MN'\parallel AD\parallel BC, AM=MB$) точка $N'$ — середина отрезка $CD$. Значит, точки $N$ и $N'$ совпадут.

 

2) Докажем формулу.

 

Проведем $BB'\perp AD, CC'\perp AD$. Пусть $BB'\cap MN=M', CC'\cap MN=N'$.

 

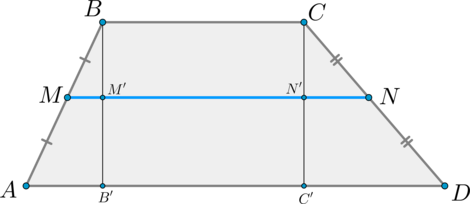
Тогда по теореме Фалеса $M'$ и $N'$ — середины отрезков $BB'$ и $CC'$ соответственно. Значит, $MM'$ – средняя линия $\triangle ABB'$, $NN'$ — средняя линия $\triangle DCC'$. Поэтому: $$MM'=\dfrac12 AB', \quad NN'=\dfrac12 DC'$$

Т.к. $MN\parallel AD\parallel BC$ и $BB', CC'\perp AD$, то $B'M'N'C'$ и $BM'N'C$ – прямоугольники. По теореме Фалеса из $MN\parallel AD$ и $AM=MB$ следует, что $B'M'=M'B$. Значит, $B'M'N'C'$ и $BM'N'C$ – равные прямоугольники, следовательно, $M'N'=B'C'=BC$.

 

Таким образом:

$$MN=MM'+M'N'+N'N=\dfrac12 AB'+B'C'+\dfrac12 C'D=$$ $$=\dfrac12 \left(AB'+B'C'+BC+C'D\right)=\dfrac12\left(AD+BC\right)$$

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

 

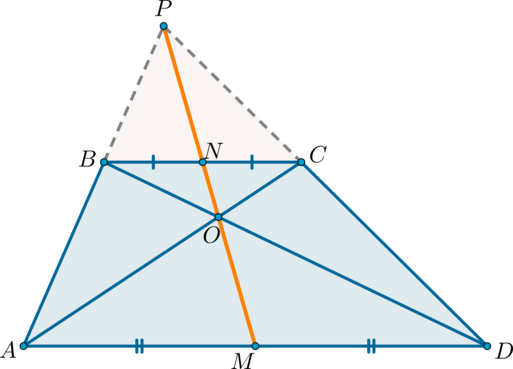
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

 

1) Докажем, что точки $P$, $N$ и $M$ лежат на одной прямой.

 

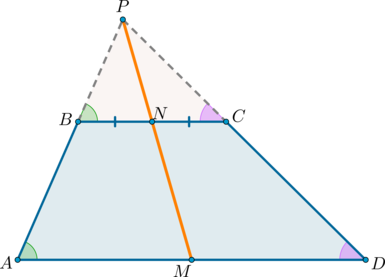
Проведем прямую $PN$ ($P$ – точка пересечения продолжений боковых сторон, $N$ – середина $BC$). Пусть она пересечет сторону $AD$ в точке $M$. Докажем, что $M$ – середина $AD$.

 

Рассмотрим $\triangle BPN$ и $\triangle APM$. Они подобны по двум углам ($\angle APM$ – общий, $\angle PAM=\angle PBN$ как соответственные при $AD\parallel BC$ и $AB$ секущей). Значит: $$\dfrac{BN}{AM}=\dfrac{PN}{PM}$$

Рассмотрим $\triangle CPN$ и $\triangle DPM$. Они подобны по двум углам ($\angle DPM$ – общий, $\angle PDM=\angle PCN$ как соответственные при $AD\parallel BC$ и $CD$ секущей). Значит: $$\dfrac{CN}{DM}=\dfrac{PN}{PM}$$

Отсюда $\dfrac{BN}{AM}=\dfrac{CN}{DM}$. Но $BN=NC$, следовательно, $AM=DM$.

 

2) Докажем, что точки $N, O, M$ лежат на одной прямой.

 

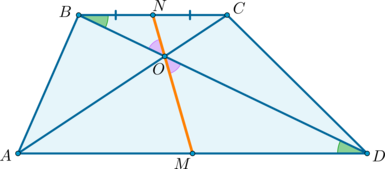
Пусть $N$ – середина $BC$, $O$ – точка пересечения диагоналей. Проведем прямую $NO$, она пересечет сторону $AD$ в точке $M$. Докажем, что $M$ – середина $AD$.

 

$\triangle BNO\sim \triangle DMO$ по двум углам ($\angle OBN=\angle ODM$ как накрест лежащие при $BC\parallel AD$ и $BD$ секущей; $\angle BON=\angle DOM$ как вертикальные). Значит: $$\dfrac{BN}{MD}=\dfrac{ON}{OM}$$

Аналогично $\triangle CON\sim \triangle AOM$. Значит: $$\dfrac{CN}{MA}=\dfrac{ON}{OM}$$

Отсюда $\dfrac{BN}{MD}=\dfrac{CN}{MA}$. Но $BN=CN$, следовательно, $AM=MD$.

$${\Large{\text{Равнобедренная трапеция}}}$$

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

 

Трапеция называется равнобедренной, если ее боковые стороны равны.

 

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

 

2) Диагонали равнобедренной трапеции равны.

 

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

 

Доказательство

1) Рассмотрим равнобедренную трапецию $ABCD$.



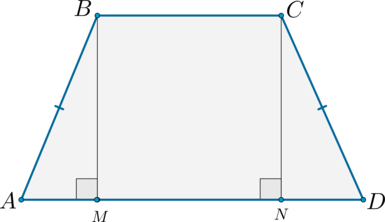
Из вершин $B$ и $C$ опустим на сторону $AD$ перпендикуляры $BM$ и $CN$ соответственно. Так как $BM\perp AD$ и $CN\perp AD$, то $BM\parallel CN$; $AD\parallel BC$, тогда $MBCN$ – параллелограмм, следовательно, $BM = CN$.

 

Рассмотрим прямоугольные треугольники $ABM$ и $CDN$. Так как у них равны гипотенузы и катет $BM$ равен катету $CN$, то эти треугольники равны, следовательно, $\angle DAB = \angle CDA$.

 

2) 

 

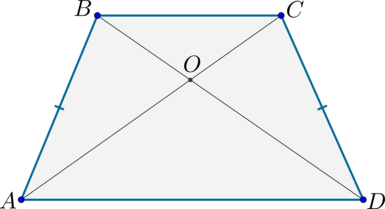
Т.к. $AB=CD, \angle A=\angle D, AD$ – общая, то по первому признаку $\triangle ABD=\triangle ACD$. Следовательно, $AC=BD$.

 

3) Т.к. $\triangle ABD=\triangle ACD$, то $\angle BDA=\angle CAD$. Следовательно, треугольник $\triangle AOD$ – равнобедренный. Аналогично доказывается, что и $\triangle BOC$ – равнобедренный.

 

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

 

2) Если у трапеции диагонали равны, то она равнобедренная.

 

Доказательство

Рассмотрим трапецию $ABCD$, такую что $\angle A = \angle D$.

 

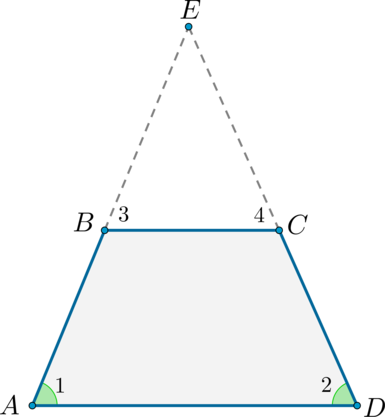
Достроим трапецию до треугольника $AED$ как показано на рисунке. Так как $\angle 1 = \angle 2$, то треугольник $AED$ равнобедренный и $AE = ED$. Углы $1$ и $3$ равны как соответственные при параллельных прямых $AD$ и $BC$ и секущей $AB$. Аналогично равны углы $2$ и $4$, но $\angle 1 = \angle 2$, тогда $\angle 3 = \angle 1 = \angle 2 = \angle 4$, следовательно, треугольник $BEC$ тоже равнобедренный и $BE = EC$.

 

В итоге $AB = AE - BE = DE - CE = CD$, то есть $AB = CD$, что и требовалось доказать.

 

2) Пусть $AC=BD$. Т.к. $\triangle AOD\sim \triangle BOC$, то обозначим их коэффициент подобия за $k$. Тогда если $BO=x$, то $OD=kx$. Аналогично $CO=y \Rightarrow AO=ky$.

 

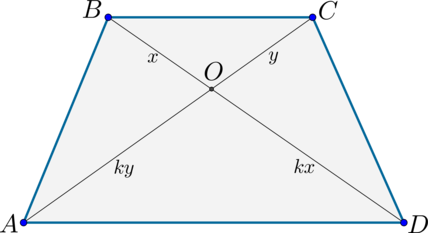
Т.к. $AC=BD$, то $x+kx=y+ky \Rightarrow x=y$. Значит $\triangle AOD$ – равнобедренный и $\angle OAD=\angle ODA$.

 

Таким образом, по первому признаку $\triangle ABD=\triangle ACD$ ($AC=BD, \angle OAD=\angle ODA, AD$ – общая). Значит, $AB=CD$, чтд.