Введение в тригонометрию

$\blacktriangleright$ Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат.

 

Угол в $1^\circ$ — это такой центральный угол, который опирается на дугу, длина которой равна $\dfrac1{360}$ длины всей окружности.

 

$\blacktriangleright$ Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси $Ox$ (на рисунке выделено красным).
На рисунке таким образом отмечены углы $45^\circ,\ 180^\circ,\ 240^\circ$:


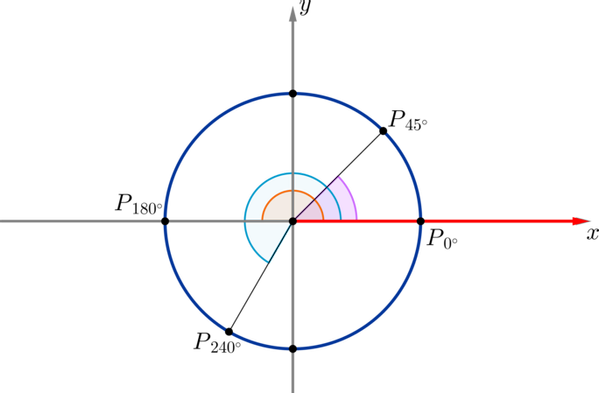
Заметим, что угол $0^\circ$ — это угол, обе стороны которого совпадают с положительным направлением оси $Ox$.

 

Точку, в которой вторая сторона такого угла $\alpha$ пересекает окружность, будет называть $P_{\alpha}$.
Положение точки $P_{0}$ будем называть начальным положением.

Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения $P_0$ до положения $P_{\alpha}$ на угол $\alpha$.

 

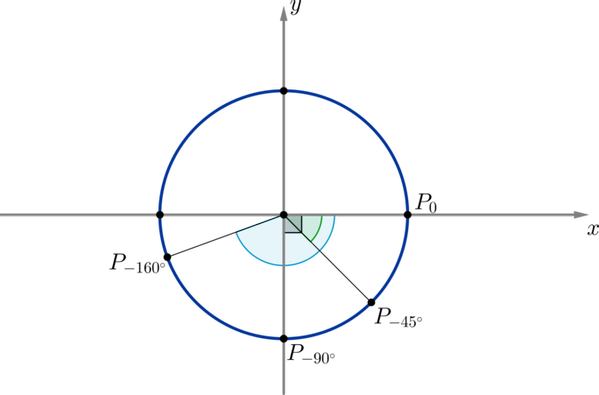
$\blacktriangleright$ Поворот по окружности против часовой стрелки — это поворот на положительный угол. Поворот по часовой стрелке — это поворот на отрицательный угол.

Например, на рисунке отмечены углы $-45^\circ, -90^\circ, -160^\circ$:

 

$\blacktriangleright$ Рассмотрим точку $P_{30^\circ}$ на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки $P_{30^\circ}$, необходимо совершить поворот на угол $30^\circ$ (оранжевый). Если мы совершим полный оборот (то есть на $360^\circ$) и еще поворот на $30^\circ$, то мы снова попадем в эту точку, хотя уже был совершен поворот на угол $390^\circ=360^\circ+30^\circ$ (голубой). Также попасть в эту точку мы можем, совершив поворот на $-330^\circ$ (зеленый), на $750^\circ=360^\circ+360^\circ+30^\circ$ и т.д.


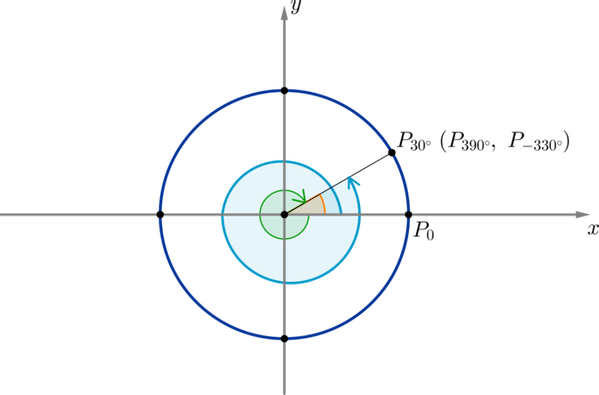
Таким образом, каждой точке на окружности соответствует бесконечное множество углов, причем отличаются эти углы друг от друга на целое число полных оборотов ($n\cdot360^\circ, n\in\mathbb{Z}$).
Например, угол $30^\circ$ на $360^\circ$ больше, чем угол $-330^\circ$, и на $2\cdot 360^\circ$ меньше, чем угол $750^\circ$.

 

Все углы, находящиеся в точке $P_{30^\circ}$ можно записать в виде: $\alpha=30^\circ+n\cdot 360^\circ, \ n\in\mathbb{Z}$.

 

$\blacktriangleright$ Угол в $1$ радиан — это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности:

 

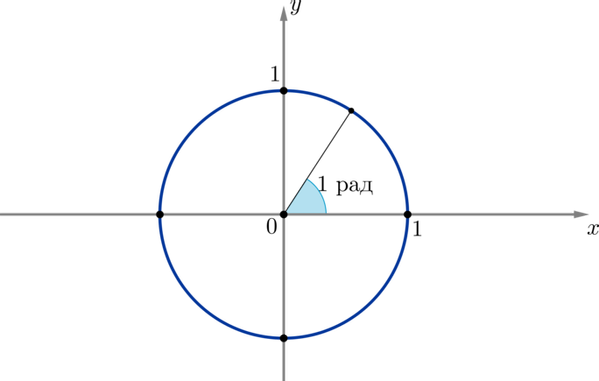
Т.к. длина всей окружности радиусом $R$ равна $2\pi R$, а в градусной мере — $360^\circ$, то имеем $360^\circ=2\pi \cdot 1\textbf{ рад}$, откуда $$180^\circ=\pi \textbf{ рад}$$ Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот.

 

Пример 1. Найти радианную меру угла $60^\circ$.

 

Т.к. $180^\circ = \pi \Rightarrow 1^\circ = \dfrac{\pi}{180} \Rightarrow 60^\circ=\dfrac{\pi}3$

 

Пример 2. Найти градусную меру угла $\dfrac34 \pi$.

 

Т.к. $\pi=180^\circ \Rightarrow \dfrac34 \pi=\dfrac34 \cdot 180^\circ=135^\circ$.

 

Обычно пишут, например, не $\dfrac{\pi}4 \text{ рад}$, а просто $\dfrac{\pi}4$ (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают. Таким образом, под записью “угол равен $1$” понимают, что “угол равен $1$ радиану”, а не “угол равен $1$ градусу”.

 

Т.к. $\pi \thickapprox 3,14 \Rightarrow 180^\circ \thickapprox 3,14 \textbf{ рад} \Rightarrow 1 \textbf{ рад} \thickapprox 57^\circ$.
Такую приблизительную подстановку делать в задачах нельзя, но знание того, чему приближенно равен $1$ радиан в градусах часто помогает при решении некоторых задач. Например, таким образом проще найти на окружности угол в $5$ радиан: он примерно равен $285^\circ$.

 

$\blacktriangleright$ Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов $0<\alpha< 90^\circ$ определены синус, косинус, тангенс и котангенс следующим образом:
если дан прямоугольный треугольник со сторонами $a, b, c$ и углом $\alpha$, то:

 

Т.к. на единичной окружности определены любые углы $\alpha\in(-\infty;+\infty)$, то нужно определить синус, косинус, тангенс и котангенс для любого угла.
Рассмотрим единичную окружность и на ней угол $\alpha$ и соответствующую ему точку $P_{\alpha}$:

 

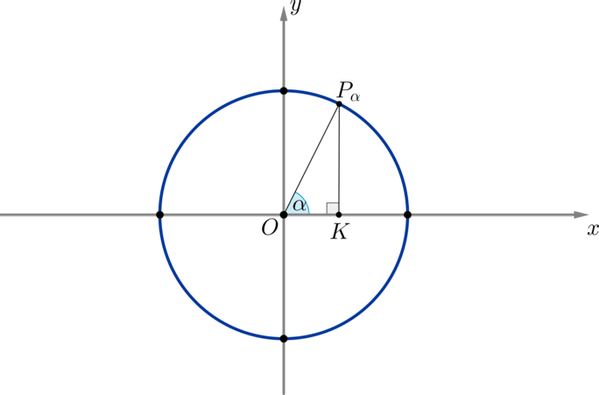
Опустим перпендикуляр $P_{\alpha}K$ из точки $P_{\alpha}$ на ось $Ox$. Мы получим прямоугольный треугольник $\triangle OP_{\alpha}K$, из которого имеем: $$\sin\alpha=\dfrac{P_{\alpha}K}{P_{\alpha}O} \qquad \cos \alpha=\dfrac{OK}{P_{\alpha}O}$$ Заметим, что отрезок $OK$ есть не что иное, как абсцисса $x_{\alpha}$ точки $P_{\alpha}$, а отрезок $P_{\alpha}K$ — ордината $y_{\alpha}$. Заметим также, что т.к. мы брали единичную окружность, то $P_{\alpha}O=1$ — ее радиус.
Таким образом, $$\sin\alpha=y_{\alpha}, \qquad \cos \alpha=x_{\alpha}$$

Таким образом, если точка $P_{\alpha}$ имела координаты $(x_{\alpha}\,;y_{\alpha})$, то через соответствующий ей угол ее координаты можно переписать как $(\cos\alpha\,;\sin\alpha)$.

 

Определение: 1. Синусом угла $\alpha$ называется ордината точки $P_{\alpha}$, соответствующей этому углу, на единичной окружности.

 

2. Косинусом угла $\alpha$ называется абсцисса точки $P_{\alpha}$, соответствующей этому углу, на единичной окружности.

 

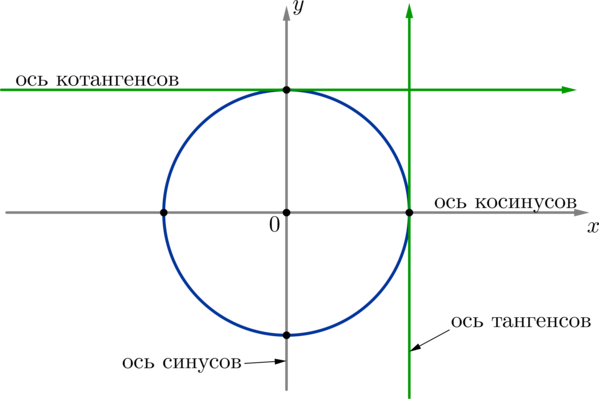
Поэтому ось $Oy$ называют осью синусов, ось $Ox$ — осью косинусов.

 

$\blacktriangleright$ Окружность можно разбить на $4$ четверти, как показано на рисунке.

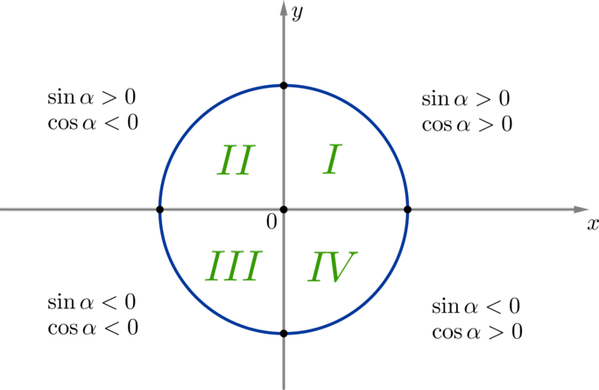
Т.к. в $I$ четверти и абсциссы, и ординаты всех точек положительны, то косинусы и синусы всех углов из этой четверти также положительны.
Т.к. во $II$ четверти ординаты всех точек положительны, а абсциссы — отрицательны, то косинусы всех углов из этой четверти — отрицательны, синусы — положительны.
Аналогично можно определить знак синуса и косинуса для оставшихся четвертей.

 

Пример 3. Так как, например, точки $P_{\frac{\pi}{6}}$ и $P_{-\frac{11\pi}6}$ совпадают, то их координаты равны, т.е. $\sin\dfrac{\pi}6=\sin \left(-\dfrac{11\pi}6\right),\ \cos \dfrac{\pi}6=\cos \left(-\dfrac{11\pi}6\right)$.

 

Пример 4. Рассмотрим точки $P_{\alpha}$ и $P_{\pi-\alpha}$. Пусть для удобства $0<\alpha<\dfrac{\pi}2$.


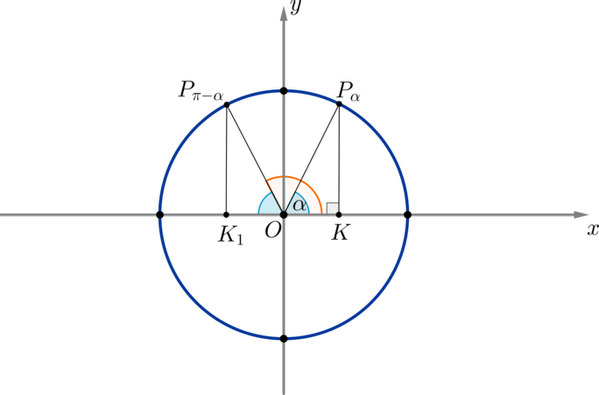
Проведем перпендикуляры на ось $Ox$: $OK$ и $OK_1$. Треугольники $OKP_{\alpha}$ и $OK_1P_{\pi-\alpha}$ равны по гипотенузе и углу ($\angle P_{\alpha}OK=\angle P_{\pi-\alpha}OK_1=\alpha$).   Следовательно, $OK=OK_1, KP_{\alpha}=K_1P_{\pi-\alpha}$.   Т.к. координаты точки $P_{\alpha}=(OK;KP_{\alpha})=(\cos\alpha\,;\sin\alpha)$, а точки $P_{\pi-\alpha}=(-OK_1;K_1P_{\pi-\alpha})=(\cos(\pi-\alpha)\,;\sin(\pi-\alpha))$, следовательно, $$\cos(\pi-\alpha)=-\cos\alpha, \qquad \sin(\pi-\alpha)=\sin\alpha$$

Таким образом доказываются и другие формулы, называемые формулами приведения: $${\large{\begin{array}{l|r} \hline \sin(\pi-\alpha)=\sin\alpha & \cos(\pi-\alpha)=-\cos\alpha\\[2ex] \sin(\pi+\alpha)=-\sin\alpha & \cos(\pi+\alpha)=-\cos\alpha\\[2ex] \sin(2\pi\pm\alpha)=\pm\sin\alpha & \cos (2\pi\pm\alpha)=\cos\alpha\\[2ex] \sin \left(\dfrac{\pi}2\pm\alpha\right)=\cos\alpha & \cos\left(\dfrac{\pi}2\pm\alpha\right)=\pm\sin\alpha\\[2ex] \hline \end{array}}}$$

С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из $I$ четверти.

 

Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
$${\large{\begin{array}{|c|c|c|c|c|c|} \hline &&&&&\\[-17pt] & \quad 0 \quad (0^ \circ)& \quad \dfrac{\pi}6 \quad (30^\circ) & \quad \dfrac{\pi}4 \quad (45^\circ) & \quad \dfrac{\pi}3 \quad (60^\circ)& \quad \dfrac{\pi}2 \quad (90^\circ) \\ &&&&&\\[-17pt] \hline \sin & 0 &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2&1\\[4pt] \hline \cos &1&\frac{\sqrt3}2&\frac{\sqrt2}2&\frac12&0\\[4pt] \hline \mathrm{tg} &0 &\frac{\sqrt3}3&1&\sqrt3&\infty\\[4pt] \hline \mathrm{ctg} &\infty &\sqrt3&1&\frac{\sqrt3}3&0\\[4pt] \hline \end{array}}}$$

Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”.

 

Пример 5. Найдите $\sin{\dfrac{3\pi}4}$.

 

Преобразуем угол: $\dfrac{3\pi}4=\dfrac{4\pi-\pi}{4}=\pi-\dfrac{\pi}4$

 

Таким образом, $\sin{\dfrac{3\pi}4}=\sin\left(\pi-\dfrac{\pi}4\right)=\sin\dfrac{\pi}4=\dfrac{\sqrt2}2$.

 

$\blacktriangleright$ Для упрощения запоминания и использования формул приведения можно следовать следующему правилу.

 

Случай 1. Если угол можно представить в виде $n\cdot \pi\pm \alpha$, где $n\in\mathbb{N}$, то $$\sin(n\cdot \pi\pm \alpha)=\bigodot \sin\alpha$$ где на месте $\bigodot$ стоит знак синуса угла $n\cdot \pi\pm \alpha$. $$\cos(n\cdot \pi\pm \alpha)=\bigodot \cos\alpha$$ где на месте $\bigodot$ стоит знак косинуса угла $n\cdot \pi\pm \alpha$.

 

Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол $\alpha$ находится в $I$ четверти.

 

Случай 2. Если угол можно представить в виде $n\cdot \pi+\dfrac{\pi}2\pm\alpha$, где $n\in\mathbb{N}$, то $$\sin(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \cos\alpha$$ где на месте $\bigodot$ стоит знак синуса угла $n\cdot \pi\pm \alpha$. $$\cos(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \sin\alpha$$ где на месте $\bigodot$ стоит знак косинуса угла $n\cdot \pi\pm \alpha$.

 

Знак определяется таким же образом, как и в случае $1$.

 

Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).

 

Пример 6. Найти $\sin \dfrac{13\pi}{3}$.

 

Преобразуем угол: $\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3$, следовательно, $\sin \dfrac{13\pi}{3}=\sin \left(4\pi+\dfrac{\pi}3\right)=\sin\dfrac{\pi}3=\dfrac{\sqrt3}2$

 

Пример 7. Найти $\cos \dfrac{17\pi}{6}$.

 

Преобразуем угол: $\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6$, следовательно, $\cos \dfrac{17\pi}{6}=\cos \left(3\pi-\dfrac{\pi}6\right)=-\cos\dfrac{\pi}6=-\dfrac{\sqrt3}2$

 

$\blacktriangleright$ Область значений синуса и косинуса.
Т.к. координаты $x_{\alpha}$ и $y_{\alpha}$ любой точки $P_{\alpha}$ на единичной окружности находятся в пределах от $-1$ до $1$, а $\cos\alpha$ и $\sin\alpha$ — абсцисса и ордината соответственно этой точки, то 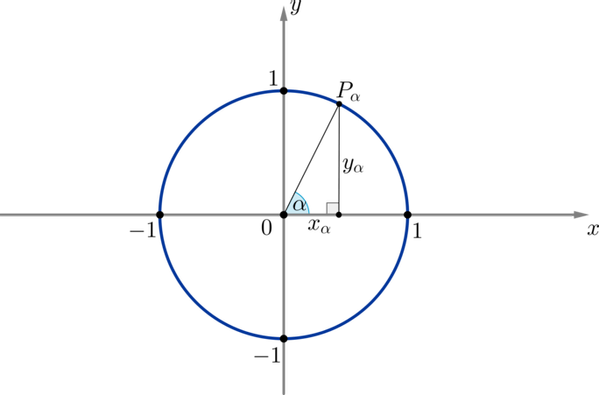$${\large{-1\leq \cos\alpha\leq 1 ,\qquad -1\leq\sin\alpha\leq 1}}$$

 

Из прямоугольного треугольника по теореме Пифагора имеем: $x^2_{\alpha}+y^2_{\alpha}=1^2$
Т.к. $x_{\alpha}=\cos\alpha,\ y_{\alpha}=\sin\alpha \Rightarrow$ $${\large{\sin^2\alpha+\cos^2\alpha=1}} - \textbf{основное тригонометрическое тождество (ОТТ)}$$

$\blacktriangleright$ Тангенс и котангенс.

 

Т.к. $\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}, \cos\alpha\ne 0$

 

$\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}, \sin\alpha\ne 0$, то:

 

1) ${\large{\mathrm{tg}\,\alpha\cdot \mathrm{ctg}\,\alpha=1, \cos\alpha\ne 0, \sin\alpha \ne 0}}$

 

2) тангенс и котангенс положительны в $I$ и $III$ четвертях и отрицательны в $II$ и $IV$ четвертях.

 

3) область значений тангенса и котангенса — все вещественные числа, т.е. $\mathrm{tg}\,\alpha\in\mathbb{R}, \ \mathrm{ctg}\,\alpha\in\mathbb{R}$

 

4) для тангенса и котангенса также определены формулы приведения.

 

Случай 1. Если угол можно представить в виде $n\cdot \pi\pm \alpha$, где $n\in\mathbb{N}$, то $$\mathrm{tg}\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm{tg}\,\alpha$$ где на месте $\bigodot$ стоит знак тангенса угла $n\cdot \pi\pm \alpha$ ($\cos\alpha\ne 0$). $$\mathrm{ctg}\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm{ctg}\,\alpha$$ где на месте $\bigodot$ стоит знак котангенса угла $n\cdot \pi\pm \alpha$ ($\sin\alpha\ne 0$).

 

Случай 2. Если угол можно представить в виде $n\cdot \pi+\dfrac{\pi}2\pm\alpha$, где $n\in\mathbb{N}$, то $$\mathrm{tg}\,(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \mathrm{ctg}\,\alpha$$ где на месте $\bigodot$ стоит знак тангенса угла $n\cdot \pi\pm \alpha$ ($\sin\alpha\ne 0$). $$\mathrm{ctg}\,(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \mathrm{tg}\,\alpha$$ где на месте $\bigodot$ стоит знак котангенса угла $n\cdot \pi\pm \alpha$ ($\cos\alpha\ne 0$).

 

5) ось тангенсов проходит через точку $(1;0)$ параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов;
ось котангенсов — через точку $(0;1)$ параллельно оси косинусов, причем положительное направление оси котангенсов совпадает с положительным направлением оси косинусов.

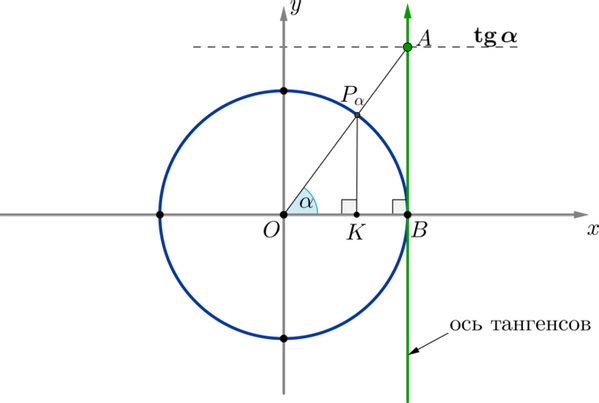
Доказательство этого факта приведем на примере оси тангенсов.

 

$\triangle OP_{\alpha}K \sim \triangle AOB \Rightarrow \dfrac{P_{\alpha}K}{OK}=\dfrac{BA}{OB} \Rightarrow \dfrac{\sin\alpha}{\cos\alpha}=\dfrac{BA}1 \Rightarrow BA=\mathrm{tg}\,\alpha$.

 

Таким образом, если точку $P_{\alpha}$ соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно $\mathrm{tg}\,\alpha$.

 

6) из основного тригонометрического тождества вытекают следующие формулы: $$1+\mathrm{tg}\,^2\alpha=\dfrac1{\cos^2\alpha},\cos\alpha\ne 0 \qquad \qquad 1+\mathrm{ctg}\,^2\alpha=\dfrac1{\sin^2\alpha}, \sin\alpha\ne 0$$ Первую формулу получают делением правой и левой частей ОТТ на $\cos^2\alpha$, вторую — делением на $\sin^2\alpha$.

 

Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это $\alpha=\dfrac{\pi}2+\pi n, n\in\mathbb{Z}$);
котангенс не определен в углах, где синус равен нулю (это $\alpha=\pi+\pi n, n\in\mathbb{Z}$).

 

$\blacktriangleright$ Четность косинуса и нечетность синуса, тангенса, котангенса.

 

Напомним, что функция $f(x)$ называется четной, если $f(-x)=f(x)$.

 

Функция называется нечетной, если $f(-x)=-f(x)$.

 

По окружности видно, что косинус угла $\alpha$ равен косинусу угла $-\alpha$ при любых значениях $\alpha$:

 

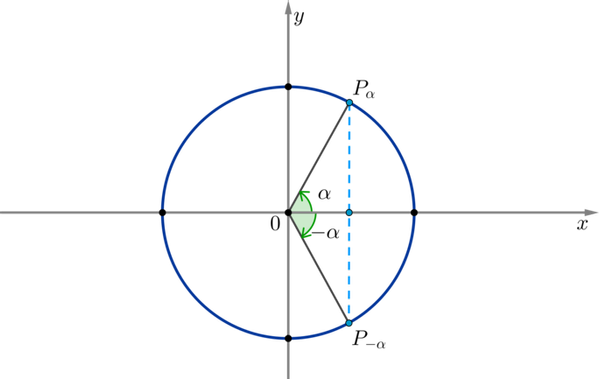
Таким образом, косинус — четная функция, значит, верна формула $${\Large{\cos(-x)=\cos x}}$$

 

По окружности видно, что синус угла $\alpha$ противоположен синусу угла $-\alpha$ при любых значениях $\alpha$:

 

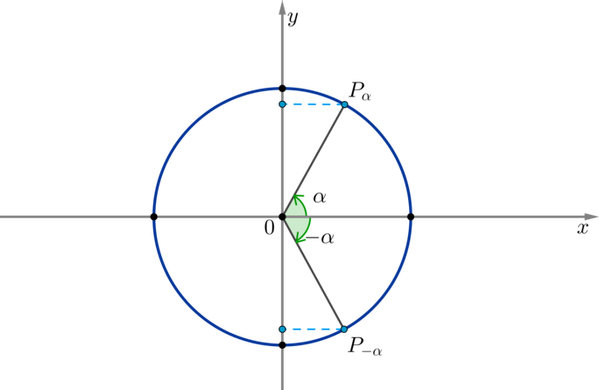
Таким образом, синус — нечетная функция, значит, верна формула $${\Large{\sin(-x)=-\sin x}}$$

Тангенс и котангенс также нечетные функции: $${\Large{\mathrm{tg}\,(-x)=-\mathrm{tg}\,x}}$$ $${\Large{\mathrm{ctg}\,(-x)=-\mathrm{ctg}\,x}}$$

 

Т.к. $\mathrm{tg}\,(-x)=\dfrac{\sin (-x)}{\cos(-x)}=\dfrac{-\sin x}{\cos x}=-\mathrm{tg}\,x \qquad \mathrm{ctg}\,(-x)=\dfrac{\cos(-x)}{\sin(-x)}=-\mathrm{ctg}\,x$)