Простейшие тригонометрические уравнения и неравенства

$\blacktriangleright$ Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
$\sin x=a,\quad \cos x=a,\quad \mathrm{tg}\,x=b,\quad \mathrm{ctg}\,x=b$, которые имеют смысл при $-1\leq a\leq 1,\quad b\in \mathbb{R}$.

 

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен $1$).

 

$${\color{red}{\text{Решение простейших тригонометрических уравнений}}}$$

Рассмотрим несколько примеров:

 

Пример 1. Решить уравнение $\sin x=\dfrac12$.

 

Найдем на оси синусов точку $\dfrac12$ и проведем прямую параллельно оси $Ox$ до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен $\dfrac12$. Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$. Тогда в нашем случае это углы $\dfrac{\pi}6$ и $\dfrac{5\pi}6$. Все остальные углы можно получить путем прибавления к данным углам $2\pi\cdot n$, где $n$ — целое число (т.е. поворотом от данных на целое число полных кругов).

 

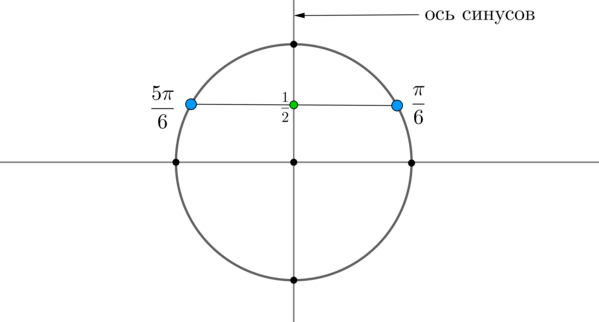
Таким образом, решением являются $x_1=\dfrac{\pi}6+2\pi n,\ x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}$.

 

Пример 2. Решить уравнение $\cos x=-\dfrac{\sqrt2}{2}$.

 

Найдем на оси косинусов точку $-\dfrac{\sqrt2}{2}$ и проведем прямую параллельно оси $Oy$ до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен $-\dfrac{\sqrt2}{2}$. Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$. Тогда в нашем случае это углы $\dfrac{3\pi}4$ и $-\dfrac{3\pi}4$. Все остальные углы можно получить путем прибавления к данным $2\pi\cdot n$, где $n$ — целое число.

 

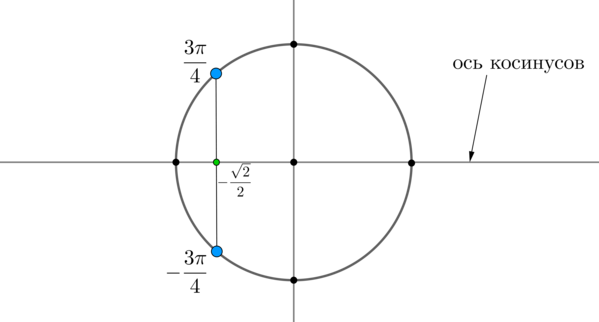
Таким образом, решением являются $x_1=\dfrac{3\pi}4+2\pi n,\ x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}$.

 

Пример 3. Решить уравнение $\mathrm{tg}\,x=\dfrac{\sqrt3}3$.

 

Найдем на оси тангенсов точку $\dfrac{\sqrt3}3$ и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен $\dfrac{\sqrt3}3$.Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$. Тогда в нашем случае это углы $\dfrac{\pi}6$ и $-\dfrac{5\pi}6$. Все остальные углы можно получить путем прибавления к данным $2\pi\cdot n$, где $n$ — целое число, или путем прибавления к одному из данных углов $\pi n$.

 

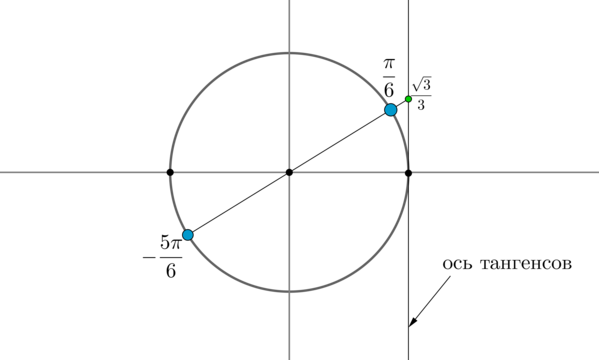
Таким образом, решением являются $x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}$.

 

Пример 4. Решить уравнение $\mathrm{ctg}\,x=\sqrt3$.

 

Найдем на оси котангенсов точку $\sqrt3$ и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен $\sqrt3$. Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка $[-\pi;\pi]$. Тогда в нашем случае это углы $\dfrac{\pi}6$ и $-\dfrac{5\pi}6$. Все остальные углы можно получить путем прибавления к данным $2\pi\cdot n$, где $n$ — целое число, или путем прибавления к одному из данных углов $\pi n$.

 

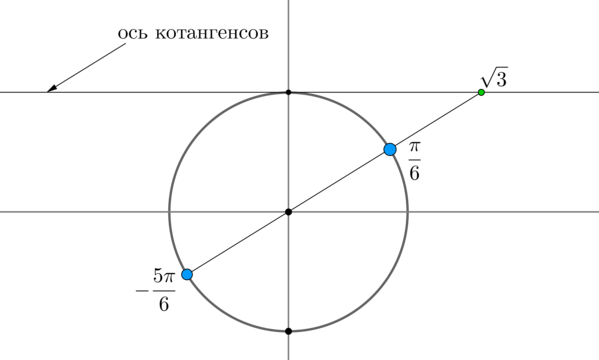
Таким образом, решением являются $x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}$.

 

$\blacktriangleright$ Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: $$\begin{array}{l|c|c} \hline \text{Уравнение} & \text{Ограничения} & \text{Решение}\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin{gathered} \begin{aligned} &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end{aligned} \end{gathered} \right. \ \ , \ n\in \mathbb{Z}\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb{Z}\\&&\\ \hline &&\\ \mathrm{tg}\, x=b & b\in \mathbb{R} & x=\mathrm{arctg}\, b+\pi n, \ n\in \mathbb{Z}\\&&\\ \hline &&\\ \mathrm{ctg}\,x=b & b\in \mathbb{R} & x=\mathrm{arcctg}\, b+\pi n, \ n\in \mathbb{Z}\\&&\\ \hline \end{array}$$ Иногда для более короткой записи решение для $\sin x=a$ записывают как $x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}$.

 

$\blacktriangleright$ Любые уравнения вида $\mathrm{G}\,\big(f(x)\big)=a$, (где $\mathrm{G}$ — одна из функций $\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}$, а аргумент $f(x)$ — некоторая функция) сводятся к стандартным уравнениям путем замены $t=f(x)$.

 

Пример 5. Решить уравнение $\sin{(\pi x+\dfrac{\pi}3)}=1$.

 

Сделав замену $t=\pi x+\dfrac{\pi}3$, мы сведем уравнение к виду $\sin t=1$. Решением данного уравнения являются $t=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}$.

 

Теперь сделаем обратную замену и получим: $\pi x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n$, откуда $x=\dfrac16+2n,\ n\in\mathbb{Z}$.

 

$${\color{red}{\text{Объединение корней}}}$$

Если $n$ точек, являющихся решением уравнения или системы, разбивают окружность на $n$ равных частей, то их можно объединить в одну формулу: $x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}$, где $\alpha$ — один из этих углов.

 

Рассмотрим данную ситуацию на примере:

 

Пример 6. Допустим, решением системы являются $x_1=\pm \dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \ n\in\mathbb{Z}$. Отметим эти точки на окружности:

 

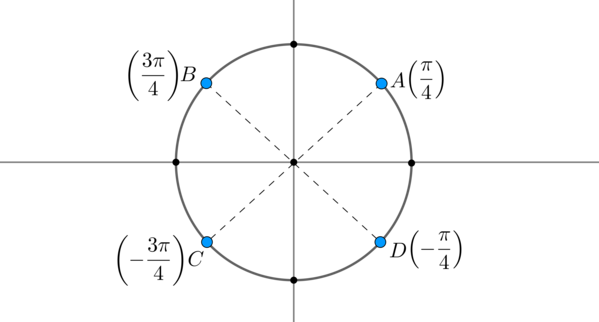
Заметим, что длины дуг $\buildrel\smile\over{AB}, \buildrel\smile\over{BC}, \buildrel\smile\over{CD}, \buildrel\smile\over{DA}$ равны $\dfrac{\pi}2$, то есть эти точки разбили окружность на $4$ равных части. Таким образом, ответ можно записать в виде одной формулы: $x=\dfrac{\pi}4+\dfrac{\pi}2n, \ n\in\mathbb{Z}$.

 

$${\color{red}{\text{Геометрическая интерпретация решений неравенств вида }\mathrm{G}\,(x) \lor a,}}$$

где $\lor$ — один из знаков $\leq,\ <,\ >,\ \geq$.

 

Пример 7. Изобразить на окружности множество решений неравенства $\sin x >\dfrac12$.

 

Для начала отметим на окружности корни уравнения $\sin x =\dfrac12$. Это точки $A$ и $B$. Все точки, синус которых больше $\dfrac12$, находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это $A$, а конец — $B$.

 

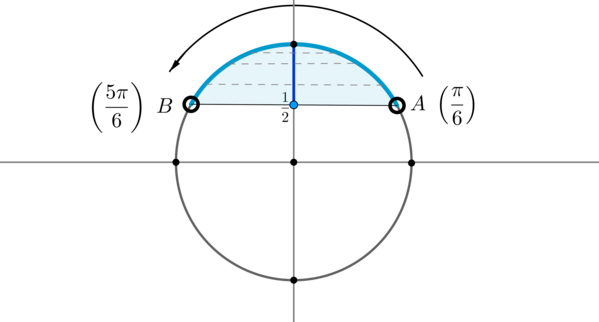
Выберем в точке $A$ любой угол, например, $\dfrac{\pi}6$. Тогда в точке $B$ необходимо выбрать угол, который будет больше $\dfrac{\pi}6$, но ближайший к нему, и чтобы синус этого угла также был равен $\dfrac12$. Это угол $\dfrac{5\pi}6$. Тогда все числа из промежутка $\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)$ являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид $\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi n\right), n\in\mathbb{Z}$, т.к. у синуса период $2\pi$.

 

Пример 8. Изобразить на окружности множество решений неравенства $\cos x <\dfrac12$.

 

Для начала отметим на окружности корни уравнения $\cos x =\dfrac12$. Это точки $A$ и $B$. Все точки, косинус которых меньше $\dfrac12$, находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это $A$, а конец — $B$.

 

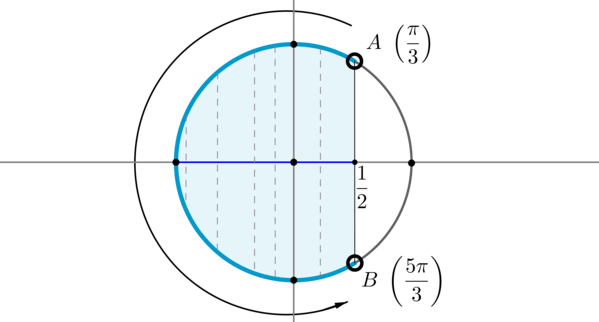
Выберем в точке $A$ любой угол, например, $\dfrac{\pi}3$. Тогда в точке $B$ необходимо выбрать угол, который будет больше $\dfrac{\pi}3$, но ближайший к нему, и чтобы косинус этого угла также был равен $\dfrac12$. Это угол $\dfrac{5\pi}3$. Тогда все числа из промежутка $\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)$ являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид $\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi n\right), n\in\mathbb{Z}$, т.к. у косинуса период $2\pi$.

 

Пример 9. Изобразить на окружности множество решений неравенства $\mathrm{tg}\, x \geq \dfrac{\sqrt{3}}3$.

 

Для начала отметим на окружности корни уравнения $\mathrm{tg}\, x = \dfrac{\sqrt{3}}3$. Это точки $A$ и $B$. Все точки, тангенс которых больше или равен $\dfrac{\sqrt{3}}3$, находятся на выделенных дугах, причем точки $C$ и $D$ выколоты, т.к. в них тангенс не определен.

 

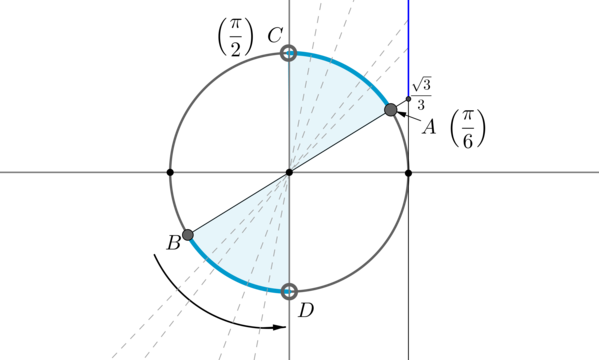
Рассмотрим одну из дуг, например, $\buildrel\smile\over{AC}$. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол $\dfrac{\pi}2$, тогда начало дуги — это угол $\dfrac{\pi}6$ (угол должен быть меньше $\dfrac{\pi}2$, но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал $\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)$. А все решения данного неравенства будут иметь вид $\Big[\dfrac{\pi}6+\pi n;\dfrac{\pi}2+\pi n\Big), n\in\mathbb{Z}$, т.к. у тангенса период $\pi$.

 

Пример 10. Изобразить на окружности множество решений неравенства $\mathrm{ctg}\, x \leq \sqrt{3}$.

 

Для начала отметим на окружности корни уравнения $\mathrm{ctg}\, x = \sqrt{3}$. Это точки $A$ и $B$. Все точки, котангенс которых меньше или равен $\sqrt{3}$, находятся на выделенных дугах, причем точки $C$ и $D$ выколоты, т.к. в них котангенс не определен.

 

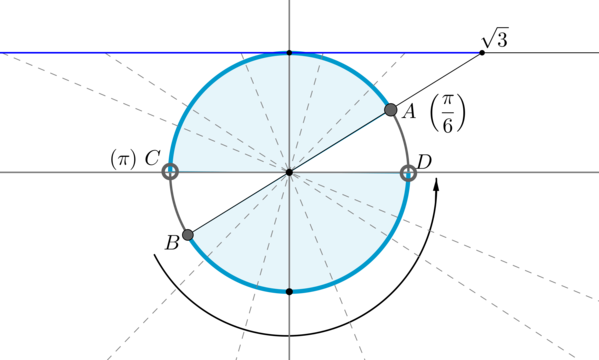
Рассмотрим одну из дуг, например, $\buildrel\smile\over{AC}$. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол $\pi$, тогда начало дуги — это угол $\dfrac{\pi}6$ (угол должен быть меньше $\pi$, но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал $\Big[\dfrac{\pi}6;\pi\Big)$. А все решения данного неравенства будут иметь вид $\Big[\dfrac{\pi}6+\pi n;\pi+\pi n\Big), n\in\mathbb{Z}$, т.к. период котангенса $\pi$.

 

$${\color{red}{\text{Отбор корней}}}$$

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

 

Пример 11. Найти корни уравнения $\sin x=-\dfrac12$, если $\cos x\ne \dfrac{\sqrt3}2$.

 

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

 

Решением первого уравнения являются $x_1=-\dfrac{\pi}6+2\pi n,\ x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}$, решением второго являются $x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}$. Отметим эти точки на окружности:

 

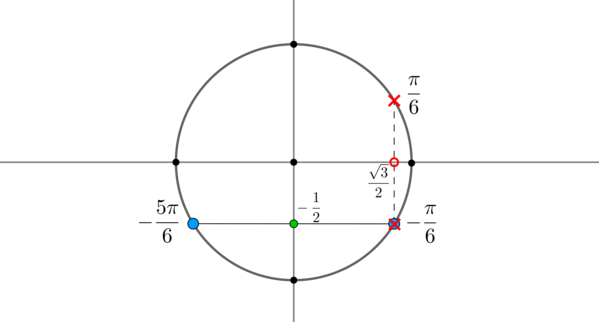
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка $x= -\dfrac{\pi}6+2\pi n$  не подходит. Следовательно, ответом будут только $x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}$.

 

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: $$\begin{aligned} &\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n - \text{ четном}\\ -\sin \alpha, \text{при } n - \text{ нечетном} \end{cases}\\ &\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n - \text{ четном}\\ -\cos \alpha, \text{при } n - \text {нечетном} \end{cases}\\ &\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\ &\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\ &\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\ &\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\ &\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\ &\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha \end{aligned}$$

 

Пример 12. Решить систему $\begin{cases} \cos x=\dfrac12\\ \sin x+\cos x>0\end{cases}$

 

Решением уравнения являются $x_1=\dfrac{\pi}3+2\pi n,\ x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}$. Подставим в неравенство $\sin x+\cos x>0$ по очереди оба корня:

$\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0$, следовательно, корень $x_1$ нам подходит;
$\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0$, следовательно, корень $x_2$ нам не подходит.

 

Таким образом, решением системы являются только $x=\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}$.

 

Алгебраический способ.

 

Пример 13. Найти корни уравнения $\sin x=\dfrac{\sqrt2}2$, принадлежащие отрезку $[0;\pi]$.

 

Решением уравнения являются $x_1=\dfrac{\pi}4+2\pi n, \ x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}$. Для того, чтобы отобрать корни, решим два неравенства: $0\leq x_1\leq\pi$ и $0\leq x_2\leq\pi$:

 

$0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38$. Таким образом, единственное целое значение $n$, удовлетворяющее этому неравенству, это $n=0$. При $n=0$ $x_1=\dfrac{\pi}4$ — входит в отрезок $[0;\pi]$.

 

Аналогично решаем неравенство $0\leq x_2\leq\pi$ и получаем $n=0$ и $x_2=\dfrac{3\pi}4$.  

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

$$ax+by=c, \quad a,b,c - \text{целые числа}$$

Уравнение будет иметь решение в целых числах относительно $x$ и $y$ тогда и только тогда, когда $c$ делится на $НОД(a,b)$.

 

Пример: Уравнение $2x+4y=3$ не имеет решений в целых числах, потому что $3$ не делится на $НОД(2,4)=2$. Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — $3$, то есть нечетное число.

 

Пример: Решить уравнение $3x+5y=2$. Т.к. $НОД(3,5)=1$, то уравнение имеет решение в целых числах. Выразим $x$ через $y$:

$$x=\dfrac{2-5y}3=\dfrac{2-2y}3-y$$

Число $\dfrac{2-2y}3$ должно быть целым. Рассмотрим остатки при делении на $3$ числа $y$: $0$, $1$ или $2$.
Если $y$ при делении на $3$ имеет остаток $0$, то оно записывается как $y=3p+0$. Тогда $$\dfrac{2-2y}3=\dfrac{2-2\cdot 3p}3=\dfrac23-2p\ne \text{целому числу}$$

Если $y$ при делении на $3$ имеет остаток $1$, то оно записывается как $y=3p+1$. Тогда $$\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}$$

Значит, этот случай нам подходит. Тогда $y=3p+1$, а $x=\dfrac{2-2y}3-y=-5p-1$.

 

Ответ: $(-5p-1; 3p+1), p\in\mathbb{Z}$.

 

Перейдем к примеру:

 

Пример 14. Решить систему $$\begin{cases} \sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt] \cos \dfrac x2=1 \end{cases}$$

Решим первое уравнение системы:

$$\left[ \begin{gathered} \begin{aligned} &\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt] &\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z}$$

Решим второе уравнение системы:

$$\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}$$

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые $n$ и $k$, при которых совпадают решения в сериях $\pi+6\pi n$ и $4\pi k$:

$$\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1$$

Т.к. $НОД(4,6)=2$ и $1$ не делится на $2$, то данное уравнение не имеет решений в целых числах.

 

Найдем целые $m$ и $k$, при которых совпадают решения в сериях $2\pi +6\pi m$ и $4\pi k$:

$$2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1$$

Данное уравнение имеет решение в целых числах. Выразим $k=\frac{3m+1}2=m+\frac{m+1}2$.

 

Возможные остатки при делении $m$ на $2$ — это $0$ или $1$.
Если $m=2p+0$, то $\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne$ целому числу.
Если $m=2p+1$, то $\frac{m+1}2=\frac{2p+1+1}2=p+1=$ целому числу.

 

Значит, $m=2p+1$, тогда $k=3p+2$, $p\in\mathbb{Z}$.

 

Подставим либо $m$, либо $k$ в соответствующую ему серию и получим окончательный ответ: $x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb{Z}$.