Решение простейших тригонометрических уравнений с помощью аркфункций

Задача 1

Решите уравнение $$\sin x=-a, \quad 0<a<1$$

Решение

$\arcsin(-a)$ – это такой угол из отрезка $\left[-\dfrac{\pi}2; \dfrac{\pi}2\right]$, синус которого равен 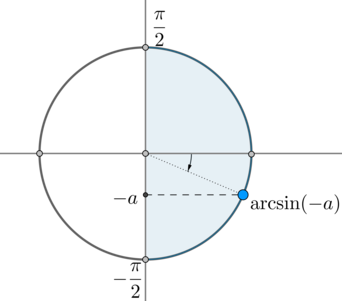$-a$: 
Следовательно, одна серия решений данного уравнения – это $x=\arcsin(-a)+2\pi n, n\in\mathbb{Z}$.
Но на окружности есть еще одна точка, синус в которой равен 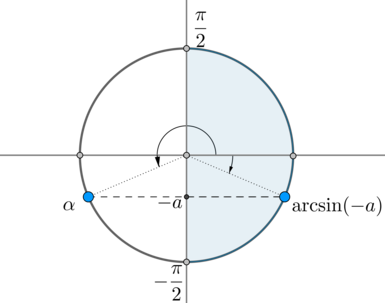$-a$ – угол $\alpha$: 
Заметим, что $\alpha=\pi+(-\arcsin(-a))$. Так как $\arcsin(-a)=-\arcsin a$, то $\alpha=\pi+\arcsin a$. Следовательно, ответ в нашем уравнении: $$\left[\begin{gathered}\begin{aligned} &x=-\arcsin a+2\pi n, n\in\mathbb{Z}\\[2ex] &x=\pi+\arcsin a+2\pi k, k\in\mathbb{Z}\end{aligned}\end{gathered}\right.$$

Задача 2

Решите уравнение $$\cos x=-a, \quad 0<a<1$$

Решение

$\arccos(-a)$ – это такой угол из отрезка $\left[0; \pi\right]$, косинус которого равен 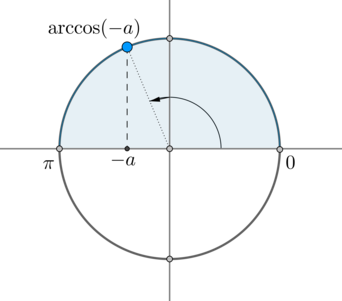$-a$: 
Следовательно, одна серия решений данного уравнения – это $x=\arccos(-a)+2\pi n, n\in\mathbb{Z}$.
Но на окружности есть еще одна точка, косинус в которой равен 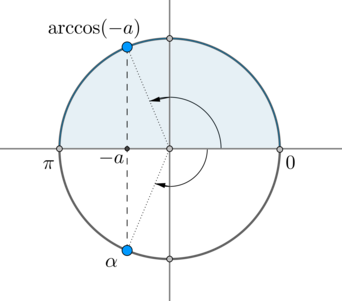$-a$ – угол $\alpha$: 
Заметим, что $\alpha=-\arccos(-a)$. Так как $\arccos(-a)=\pi-\arccos a$, то $\alpha=-\pi+\arccos a$. Следовательно, ответ в нашем уравнении: $$\left[\begin{gathered}\begin{aligned} &x=\pi-\arccos a+2\pi n, n\in\mathbb{Z}\\[2ex] &x=-\pi+\arccos a+2\pi k, k\in\mathbb{Z}\end{aligned}\end{gathered}\right.$$

Задача 3

Решите уравнение $$\mathrm{tg}\, x=-a, a>0$$

Решение

$\mathrm{arctg}\,(-a)$ – это такой угол из промежутка $\left(-\dfrac{\pi}2;\dfrac{\pi}2\right)$, тангенс которого равен 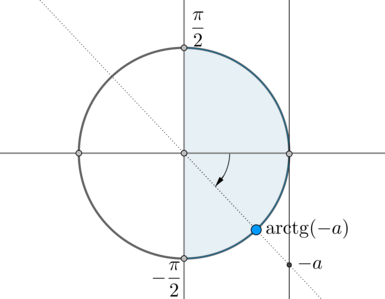$-a$: 
Следовательно, одна серия решений данного уравнения – это $x=\mathrm{arctg}\,(-a)+2\pi n, n\in\mathbb{Z}$.
Но на окружности есть еще одна точка, тангенс в которой равен 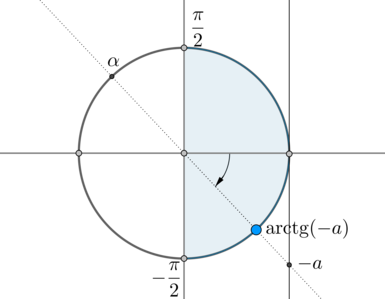$-a$ – угол $\alpha$: 
Заметим, что $\alpha=\mathrm{arctg}\,(-a)+\pi$. Так как $\mathrm{arctg}\,(-a)=-\mathrm{arctg}\, a$, то $\alpha=\pi-\mathrm{arctg}\, a$. Следовательно, ответ в нашем уравнении: $$\left[\begin{gathered}\begin{aligned} &x=-\mathrm{arctg}\, a+2\pi n, n\in\mathbb{Z}\\[2ex] &x=\pi-\mathrm{arctg}\, a+2\pi k, k\in\mathbb{Z}\end{aligned}\end{gathered}\right.$$ Заметим, что так как углы $-\mathrm{arctg}\, a$ и $\pi-\mathrm{arctg}\, a$ отличаются друг от друга на $\pi$, то ответ можно записать в виде одной серии корней с периодом $\pi$: $$x=-\mathrm{arctg}\, a+\pi m, m\in\mathbb{Z}$$

Задача 4

Решите уравнение $$\mathrm{ctg}\, x=-a, a>0$$

Решение

$\mathrm{arcctg}\,(-a)$ – это такой угол из промежутка $\left(0;\pi\right)$, котангенс которого равен 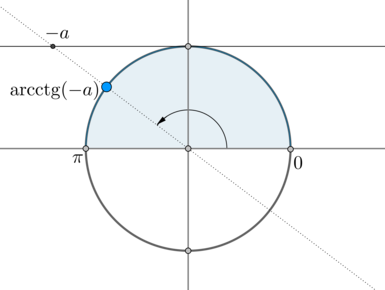$-a$: 
Следовательно, одна серия решений данного уравнения – это $x=\mathrm{arcctg}\,(-a)+2\pi n, n\in\mathbb{Z}$.
Но на окружности есть еще одна точка, котангенс в которой равен 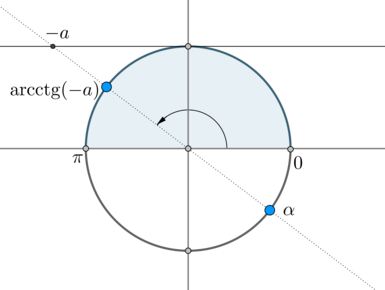$-a$ – угол $\alpha$: 
Заметим, что $\alpha=\mathrm{arcctg}\,(-a)+\pi$. Так как $\mathrm{arcctg}\,(-a)=\pi-\mathrm{arcctg}\, a$, то $\alpha=2\pi-\mathrm{arcctg}\, a$. Следовательно, ответ в нашем уравнении: $$\left[\begin{gathered}\begin{aligned} &x=\pi-\mathrm{arcctg}\, a+2\pi n, n\in\mathbb{Z}\\[2ex] &x=2\pi-\mathrm{arcctg}\, a+2\pi k, k\in\mathbb{Z}\end{aligned}\end{gathered}\right.$$ Заметим, что так как углы $2\pi-\mathrm{arcctg}\, a$ и $\pi-\mathrm{arcctg}\, a$ отличаются друг от друга на $\pi$, то ответ можно записать в виде одной серии корней с периодом $\pi$: $$x=\pi-\mathrm{arcctg}\, a+\pi m, m\in\mathbb{Z}$$