Ромб

Определение

Ромб – это параллелограмм, у которого все стороны равны.

 

Таким образом, ромб обладает всеми свойствами параллелограмма:

 

$\sim$ противоположные углы ромба попарно равны;

$\sim$ соседние углы ромба в сумме дают $180^\circ$;

$\sim$ диагонали точкой пересечения делятся пополам.

 

Теорема: свойство ромба

Диагонали ромба перпендикулярны и делят его углы пополам.

 

Доказательство

Рассмотрим ромб $ABCD$.

 

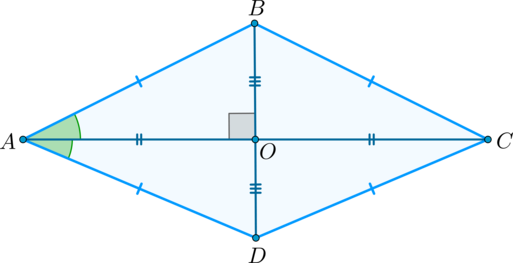
По определению ромба $AB = AD$, поэтому треугольник $BAD$ равнобедренный. Так как ромб – параллелограмм, то его диагонали точкой $O$ пересечения делятся пополам. Следовательно, $AO$ – медиана равнобедренного треугольника $BAD$, а значит, высота и биссектриса этого треугольника. Поэтому $AC\perp BD$ и $\angle BAC = \angle DAC$.

 

Теорема: признаки ромба

1. Если в параллелограмме диагонали перпендикулярны, то это – ромб.

 

2. Если в параллелограмме диагонали делят его углы пополам, то это – ромб.

 

3. Если в выпуклом четырехугольнике все стороны равны, то он – ромб.

 

Доказательство

1) Рассмотрим параллелограмм $ABCD$. Пусть $AC\perp BD$.

 

Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике $ABD$ отрезок $AO$ – медиана. Т.к. к тому же $AO$ – высота (следует из условия), то $\triangle ABD$ – равнобедренный, т.е. $AB=AD$. Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.

 

2) Пусть $AC$ – биссектриса угла $\angle A$.

 

Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике $ABD$ отрезок $AO$ – медиана. Т.к. к тому же $AO$ – биссектриса (следует из условия), то $\triangle ABD$ – равнобедренный, т.е. $AB=AD$. Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.

 

3) Пусть $ABCD$ – произвольный четырехугольник и $AB=BC=CD=AD$.

 

Т.к. противоположные стороны четырехугольника попарно равны, то он – параллелограмм. Т.к. у него все стороны равны, то по определению это ромб.