Прямоугольник и квадрат

$${\Large{\text{Прямоугольник}}}$$

Определение

Прямоугольник – это параллелограмм, у которого один угол прямой.

 

Таким образом, прямоугольник обладает всеми свойствами параллелограмма:

 

$\sim$ противоположные стороны попарно равны;

$\sim$ диагонали точкой пересечения делятся пополам.

 

Теоремы: свойства прямоугольника

1) Все углы прямоугольника прямые.

 

2) Диагонали прямоугольника равны.

 

Доказательство

1) Пусть $\angle A=90^\circ$. Т.к. в параллелограмме сумма соседних углов равна $180^\circ$, то $\angle B=180^\circ-\angle A=90^\circ$.

 

Т.к. в параллелограмме противоположные углы равны, то $\angle C=\angle A=90^\circ, \angle D=\angle B=90^\circ$, чтд.

 

2) Рассмотрим прямоугольник $ABCD$.

 

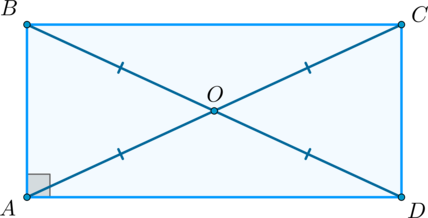
Прямоугольные треугольники $ACD$ и $DBA$ равны по двум катетам ($CD = BA$, $AD$ – общий катет). Отсюда следует, что гипотенузы этих треугольников равны, т.е. $AC = BD$.

 

Следствие

Таким образом, половинки диагоналей в прямоугольнике равны, т.е. $OA=OB=OC=OD$.

 

Теоремы: признаки прямоугольника

1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

 

2) Если в выпуклом четырехугольнике все углы прямые, то он – прямоугольник.

 

Доказательство

1) Пусть в параллелограмме $ABCD$ диагонали равны.

 

Треугольники $ABD$ и $DCA$ равны по трем сторонам ($AB = CD$, $BD = AC$, $AD$ – общая сторона). Отсюда следует, что $\angle A = \angle D$. Так как в параллелограмме противоположные углы равны, то $\angle A = \angle C$ и $\angle B = \angle D$. Таким образом, $\angle A = \angle B = \angle C = \angle D$. Параллелограмм – выпуклый четырехугольник, поэтому $\angle A + \angle B + \angle C + \angle D = 360^\circ$. Следовательно, $\angle A = \angle B = \angle C = \angle D = 90^\circ$.

 

2) Рассмотрим четырехугольник $ABCD$:

 

Т.к. $\angle A+\angle B=180^\circ$ – односторонние углы при прямых $AD$ и $BC$ и секущей $AB$, следовательно, $AD\parallel BC$.

 

Аналогично доказывается, что $AB\parallel CD$. Значит, $ABCD$ – параллелограмм. Т.к. у него к тому же все углы прямые, то по определению это прямоугольник.  

$${\Large{\text{Квадрат}}}$$

Определение

Два эквивалентных определения квадрата:

 

Квадрат – это прямоугольник, у которого все стороны равны.

Квадрат – это ромб, у которого один угол прямой.

 

Свойства квадрата

Так как квадрат является прямоугольником и ромбом, то он обладает всеми свойствами прямоугольника и ромба:

 

$\sim$ Все углы квадрата равны $90^\circ$;

$\sim$ Все стороны квадрата равны;

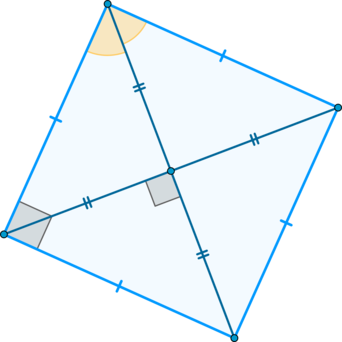
$\sim$ Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.