Вписанная окружность (описанный треугольник, описанный четырехугольник)

Факт 1.
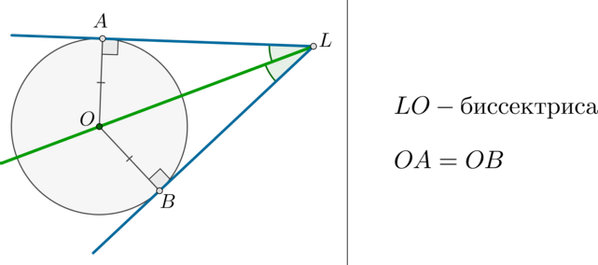
$\bullet$ Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла.
$\bullet$ Каждая точка биссектрисы угла равноудалена от его сторон.

Факт 2.
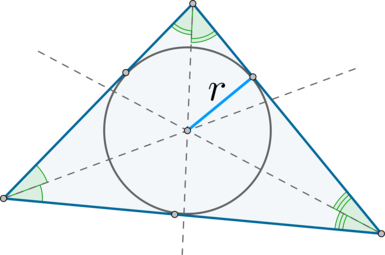
$\bullet$ Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис углов треугольника.

Факт 3.
$\bullet$ Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
$\bullet$ Наоборот: если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Центр вписанной окружности лежит на пересечении биссектрис углов четырехугольника.

Факт 4.
$\bullet$ Центр вписанной в многоугольник окружности лежит на пересечении биссектрис его углов.
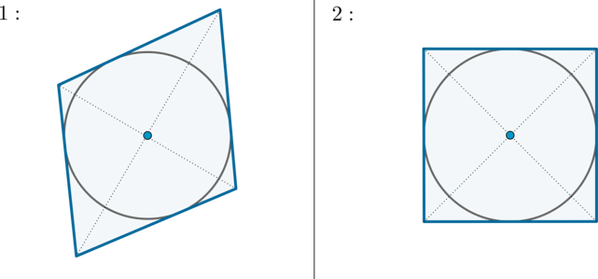
$\bullet$ 1. Если в параллелограмм можно вписать окружность, то он является ромбом.
Тогда центр окружности лежит на пересечении диагоналей.
$\bullet$ 2. Если в прямоугольник можно вписать окружность, то он является квадратом.
Тогда центр окружности лежит на пересечении диагоналей.