Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

 

$\blacktriangleright$ Основные тождества: $$\begin{array}{|l|l|} \hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos \alpha} &\mathrm{ctg}\, \alpha =\dfrac{\cos \alpha}{\sin \alpha} \\&\\ 1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} & 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end{array}$$

$\blacktriangleright$ Формулы сложения углов: $$\begin{array}{|l|r|} \hline &\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm{tg}\, (\alpha\pm \beta)=\dfrac{\mathrm{tg}\, \alpha\pm \mathrm{tg}\, \beta}{1 \mp \mathrm{tg}\, \alpha\cdot \mathrm{tg}\, \beta} & \mathrm{ctg}\, (\alpha\pm\beta)=-\dfrac{1\mp \mathrm{ctg}\, \alpha\cdot \mathrm{ctg}\, \beta}{\mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta}\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end{array}$$

$\blacktriangleright$ Формулы двойного и тройного углов: $$\begin{array}{|lc|cr|} \hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\ & & & \cos{2\alpha}=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\, \alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha = \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin {3\alpha}=3\sin \alpha -4\sin^3\alpha && & \cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end{array}$$

$\blacktriangleright$ Формулы понижения степени: $$\begin{array}{|lc|cr|} \hline &&&\\ \sin^2\alpha=\dfrac{1-\cos{2\alpha}}2 &&& \cos^2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\ \hline \end{array}$$

$\blacktriangleright$ Формулы произведения функций: $$\begin{array}{|c|} \hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}+\cos{(\alpha+\beta)}\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin{(\alpha-\beta)}+\sin{(\alpha+\beta)}\bigg)\\\\ \hline \end{array}$$

$\blacktriangleright$ Формулы суммы/разности функций: $$\begin{array}{|lc|cr|} \hline &&&\\ \sin\alpha+\sin\beta=2\sin{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \sin\alpha-\sin\beta=2\sin{\dfrac{\alpha-\beta}2}\cos{\dfrac{\alpha+\beta}2}\\&&&\\ \cos\alpha+\cos\beta=2\cos{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \cos\alpha -\cos\beta=-2\sin{\dfrac{\alpha-\beta}2}\sin{\dfrac{\alpha+\beta}2}\\&&&\\ \mathrm{tg}\, \alpha \pm \mathrm{tg}\, \beta=\dfrac{\sin{(\alpha\pm\beta)}}{\cos\alpha\cos\beta} &&& \mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta= - \dfrac{\sin{(\alpha\pm \beta)}}{\sin\alpha\sin\beta}\\&&&\\ \hline \end{array}$$

$\blacktriangleright$ Выражение синуса и косинуса через тангенс половинного угла: $$\begin{array}{|l|r|} \hline &\\ \sin{2\alpha}=\dfrac{2\mathrm{tg}\, \alpha}{1+\mathrm{tg}^2\, \alpha} & \cos{2\alpha}=\dfrac{1-\mathrm{tg}^2\, \alpha}{1+\mathrm{tg}^2\, \alpha}\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end{array}$$

$\blacktriangleright$ Формула вспомогательного аргумента: $$\begin{array}{|c|} \hline \text{Частный случай}\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin{\left(\alpha\pm \dfrac{\pi}4\right)}\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin{\left(\alpha\pm \dfrac{\pi}6\right)}\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin{\left(x\pm \dfrac{\pi}3\right)}\\\\ \hline \text{Общий случай}\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt{a^2+b^2}\cdot \sin{(\alpha\pm \phi)}, \ \ \cos\phi=\dfrac a{\sqrt{a^2+b^2}}, \ \sin\phi=\dfrac b{\sqrt{a^2+b^2}}\\\\ \hline \end{array}$$

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

 

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

 

$\blacktriangleright$ Вывод формулы косинуса разности углов $\cos{(\alpha -\beta)}=\cos\alpha\cos\beta+\sin\alpha\sin\beta$

 

Рассмотрим тригонометрическую окружность и на ней углы $\alpha$ и $\beta$. Пусть этим углам соответствуют точки $A$ и $B$ соответственно. Тогда координаты этих точек: $A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)$.

 

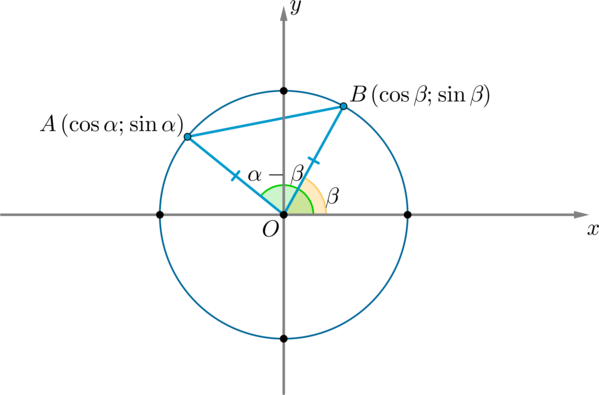
Рассмотрим $\triangle AOB: \ \angle AOB=\alpha-\beta$. По теореме косинусов:

 

$AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)$  (т.к. $AO=BO=R$ – радиус окружности)

 

По формуле расстояния между двумя точками на плоскости:

 

$AB^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2=\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta+$

$+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta=\big(\cos^2\alpha+\sin^2\alpha\big)+\big(\cos^2\beta+\sin^2\beta\big)-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=$

$=1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big) \ (2)$

 

Таким образом, сравнивая равенства $(1)$ и $(2)$:

$1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=1+1-2\cos(\alpha-\beta)$

 

Отсюда и получается наша формула.

 

$\blacktriangleright$ Вывод остальных формул суммы/разности углов:

 

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения $\sin x=\cos(90^\circ-x)$ и $\cos x=\sin (90^\circ-x)$:

 

1) $\cos(\alpha+\beta)=\cos(\alpha-(-\beta))=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$

 

2) $\sin(\alpha+\beta)=\cos(90^\circ-(\alpha+\beta))=\cos((90^\circ-\alpha)-\beta)=$

$+\cos(90^\circ-\alpha)\cos\beta+\sin(90^\circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta$

 

3) $\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\sin(-\beta)\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha$

 

4) $\mathrm{tg}\,(\alpha\pm\beta)=\dfrac{\sin (\alpha\pm\beta)}{\cos (\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=$

 

разделим числитель и знаменатель дроби на $\cos\alpha\cos\beta\ne 0$
(при $\cos\alpha=0 \Rightarrow \mathrm{tg}\,(\alpha\pm\beta)=\mp \mathrm{ctg}\,\beta$, при $\cos\beta=0 \Rightarrow \mathrm{tg}\,(\alpha\pm\beta)=\pm \mathrm{ctg}\,\alpha$):

 

$=\dfrac{\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta}{1\mp\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}$

 

Таким образом, данная формула верна только при $\cos\alpha\cos\beta\ne 0$.

 

5) Аналогично, только делением на $\sin\alpha\sin\beta\ne 0$, выводится формула котангенса суммы/разности двух углов.

 

$\blacktriangleright$ Вывод формул двойного и тройного углов:

 

Данные формулы выводятся с помощью предыдущих формул:

 

1) $\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha$

 

2) $\cos2\alpha=\cos(\alpha+\alpha)=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha=\cos^2\alpha-\sin^2\alpha$

 

Используя основное тригонометрическое тождество $\sin^2\alpha+\cos^2\alpha=1$, получим еще две формулы для косинуса двойного угла:

 

2.1) $\cos2\alpha=\cos^2\alpha-\sin^2\alpha=\cos^2\alpha-(1-\cos^2\alpha)=2\cos^2\alpha-1$

 

2.2) $\cos2\alpha=\cos^2\alpha-\sin^2\alpha=(1-\sin^2\alpha)-\sin^2\alpha=1-2\sin^2\alpha$

 

3) $\mathrm{tg}\,2\alpha=\dfrac{\sin2\alpha}{\cos2\alpha}=\dfrac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=$

 

разделим числитель и знаменатель дроби на $\cos^2\alpha\ne 0$ (при $\cos\alpha=0 \Rightarrow \mathrm{tg}\,2\alpha=0$):

 

$=\mathrm{tg}\,2\alpha=\dfrac{2\mathrm{tg}\,\alpha}{1-\mathrm{tg}^2\,\alpha}$

 

Таким образом, эта формула верна только при $\cos\alpha\ne 0$, а также при $\cos2\alpha\ne 0$ (чтобы существовал сам $\mathrm{tg}\,2\alpha$).

 

4) $\mathrm{ctg}\,2\alpha=\dfrac{\cos^2\alpha-\sin^2\alpha}{2\sin\alpha\cos\alpha}=\dfrac{\mathrm{ctg}^2\,\alpha-1}{2\mathrm{ctg}\,\alpha}$

 

По тем же причинам при $\sin\alpha\ne 0, \sin2\alpha\ne 0$.

 

5) $\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=$

$=\sin\alpha-2\sin^3\alpha+2\sin\alpha(1-\sin^2\alpha)=3\sin\alpha-4\sin^3\alpha$

 

6) Аналогично выводится, что $\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha$

 

$\blacktriangleright$ Вывод формул понижения степени:

 

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

 

1) $\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac{1+\cos2\alpha}2$

 

2) $\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac{1-\cos2\alpha}2$

 

Заметим, что в данных формулах степень синуса/косинуса равна $2$ в левой части, а в правой части степень косинуса равна $1$.

 

$\blacktriangleright$ Вывод формул произведения функций:

 

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

 

$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$

 

$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$

 

Получим: $\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)$

 

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

 

$\sin\alpha\sin\beta=\dfrac12\Big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\Big)$

 

3) Сложим формулы синуса суммы и синуса разности двух углов:

 

$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha$

 

$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha$

 

Получим: $\sin\alpha\cos\beta=\dfrac12\Big(\sin(\alpha-\beta)+\sin(\alpha+\beta)\Big)$

 

$\blacktriangleright$ Вывод формул суммы/разности функций:

 

Обозначим $\alpha+\beta=x, \alpha-\beta=y$. Тогда: $\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2$. Подставим эти значения в предыдущие три формулы:

 

1) $2\cos{\dfrac{x+y}2}\cos{\dfrac{x-y}2}=\cos x+\cos y$

 

Получили формулу суммы косинусов.

 

2) $2\sin {\dfrac{x+y}2}\sin {\dfrac{x-y}2}=\cos y-\cos x$

 

Получили формулу разности косинусов.

 

3) $2\sin {\dfrac{x+y}2}\cos {\dfrac{x-y}2}=\sin y+\sin x$

 

Получили формулу суммы синусов.

 

4) Формулу разности синусов можно вывести из формулы суммы синусов:

 

$\sin x-\sin y=\sin x+\sin(-y)=2\sin {\dfrac{x-y}2}\cos {\dfrac{x+y}2}$

 

5) $\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta=\dfrac{\sin\alpha}{\cos\alpha}\pm\dfrac{\sin\beta}{\cos\beta}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta}=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}$

 

Аналогично выводится формула суммы котангенсов.

 

$\blacktriangleright$ Вывод формул выражения синуса и косинуса через тангенс половинного угла:

 

1) $\sin2\alpha=\dfrac{\sin2\alpha}1=\dfrac{2\sin\alpha\cos\alpha}{\sin^2\alpha+\cos^2\alpha}=$

 

(разделим числитель и знаменатель дроби на $\cos^2\alpha\ne 0$ (при $\cos\alpha=0$ и $\sin2\alpha=0$):)

 

$=\dfrac{2\mathrm{tg}\,\alpha}{1+\mathrm{tg}^2\,\alpha}$

 

2) Так же, только делением на $\sin^2\alpha$, выводится формула для косинуса.

 

$\blacktriangleright$ Вывод формул вспомогательного угла:

 

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

 

Рассмотрим выражение $a\sin x+b\cos x$. Домножим и разделим это выражение на $\sqrt{a^2+b^2}\,$:

 

$a\sin x+b\cos x=\sqrt{a^2+b^2}\left(\dfrac a{\sqrt{a^2+b^2}}\sin x+ \dfrac b{\sqrt{a^2+b^2}}\cos x \right)=\sqrt{a^2+b^2}\big(a_1\sin x+b_1\cos x\big)$

 

Заметим, что таким образом мы добились того, что $a_1^2+b_1^2=1$,   т.к. $\left(\dfrac a{\sqrt{a^2+b^2}}\right)^2+\left(\dfrac b{\sqrt{a^2+b^2}}\right)^2=\dfrac{a^2+b^2}{a^2+b^2}=1$

 

Таким образом, можно утверждать, что существует такой угол $\phi$, для которого, например, $\cos \phi=a_1, \ \sin \phi=b_1$. Тогда наше выражение примет вид:

 

$\sqrt{a^2+b^2}\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt{a^2+b^2}\,\sin (x+\phi)$ (по формуле синуса суммы двух углов)

 

Значит, формула выглядит следующим образом: $${\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac a{\sqrt{a^2+b^2}}$$ Заметим, что мы могли бы, например, принять за $\cos \phi=b_1, \ \sin \phi=a_1$ и тогда формула выглядела бы как $$a\sin x+b\cos x=\sqrt{a^2+b^2}\,\cos (x-\phi)$$

 

$\blacktriangleright$ Рассмотрим некоторые частные случаи формул вспомогательного угла:

 

$a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1{\sqrt2}\sin x\pm\dfrac1{\sqrt2}\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac{\pi}4\right)$

 

$b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac{\sqrt3}2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac{\pi}6\right)$

 

$c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac{\sqrt3}2\cos x\right)=2\,\sin\left(x\pm\dfrac{\pi}3\right)$