Главная
Теория
Теория по ЕГЭ - Математика
Тригонометрические формулы. Таблица углов. Формулы приведения

Алгебра. Краткий справочник. Формулы

Тригонометрические формулы. Таблица углов. Формулы приведения

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Алгебра. Краткий справочник. Формулы

Теоретическая справка

#532

Факт 1.
$∙$ Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:

Факт 2.
$∙$ Знаки синуса, косинуса:

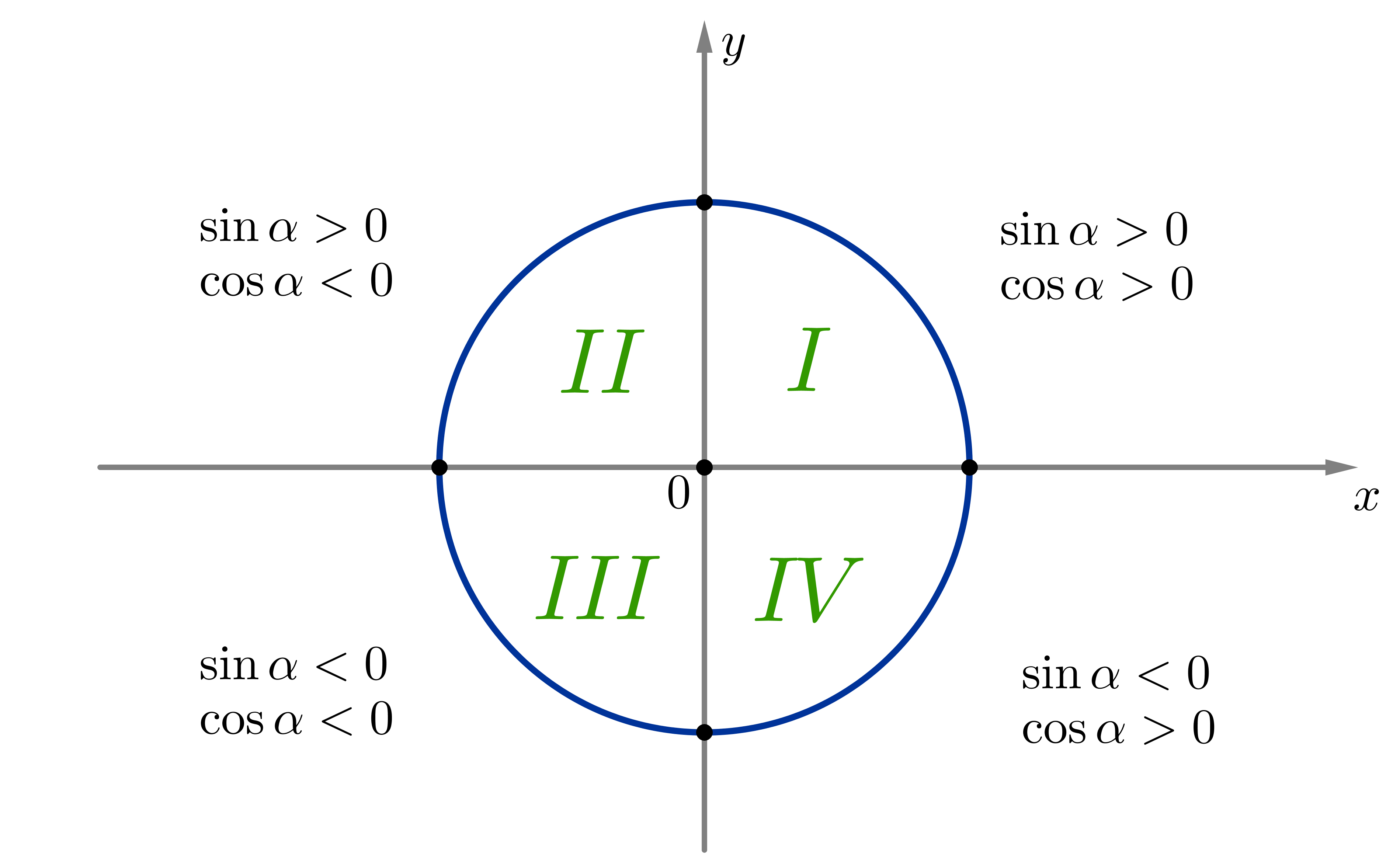
Так как $sinα- tgα = cosα$ и $cosα ctg α= sinα$ , то тангенс и котангенс положительны в $I$ и $III$ четвертях и отрицательны во $II$ и $IV$ четвертях.

Факт 3.
Формулы приведения.
$∙$ Случай 1. Если угол можно представить в виде $n⋅π± α$ , где $n∈ ℕ$ , то

⊙ sin(n ⋅π± α)= sin α

где на месте $⊙$ стоит знак синуса угла $n⋅π ±α$ .

⊙ cos(n ⋅π± α)= cosα

где на месте $⊙$ стоит знак косинуса угла $n⋅π± α$ .
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол $α$ находится в $I$ четверти.
$∙$ Случай 2. Если угол можно представить в виде $π- n⋅π + 2 ± α$ , где $n∈ ℕ$ , то

( π- ) ⊙ sin n⋅π+ 2 ± α = cosα

где на месте $⊙$ стоит знак синуса угла $π n⋅π + 2 ± α$ .

( π ) ⊙ cos n⋅π + 2 ± α = sinα

где на месте $⊙$ стоит знак косинуса угла $n⋅π+ π-± α 2$ .
Знак определяется таким же образом, как и в случае $1$ .

Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Алгоритм применения формул приведения для тангенса и котангенса полностью аналогичен.

Пример 1. Найти $13π cos 3$ .

Преобразуем угол: $13π = 12π-+-π= 4π + π- 3 3 3$ , следовательно, $13π ( π) π 1 cos-3- = cos 4π + 3- = cos-3 = 2$

Пример 2. Найти $sin 17π- 6$ .

Преобразуем угол: $17π 18π − π π -6- = --6---= 3π − 6-$ , следовательно, $sin 17π = sin(3π− π-)= sin π-= 1 6 6 6 2$

Пример 3. Найти $15π tg -4-$ .

Преобразуем угол: $15π = 16π-−-π= 4π − π- 4 4 4$ , следовательно, $15π ( π) π tg-4- = tg 4π− 4- = −tg4-= −1$

Пример 4. Найти $ctg 19π- 3$ .

Преобразуем угол: $19π = 18π-+-π= 6π + π- 3 3 3$ , следовательно, $19π ( π) π √3- ctg-3- = ctg 6π + 3-= ctg3-= -3-$

Предыдущая справка

Следующая справка