Тема КОМБИНАТОРИКА

Комбинаторная геометрия

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела комбинаторика

Разделы подтемы Комбинаторная геометрия

Расположение точек, отрезков и прямых

Пересечение отрезков и прямых

Общая точка, прямая, покрытие. Теорема Хелли

Разрезания и геометрические конструкции в текстовых

Конструктивы в комбигео

Принцип крайнего, индукция и другие методы в комбигео

Клетчатая решётка (координатная плоскость) и точки, отрезки, прямые на ней

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#111174

При каких натуральных $n$ существует выпуклый $n$ -угольник с вершинами в узлах целочисленной решётки, у которого все стороны равны $100?$

Показать ответ и решение

Каждая сторона многоугольника задаётся вектором $(x,y)$ с целыми координатами, удовлетворяющими условию:

2 2 2 x + y = 100 = 10000

Все целочисленные решения, полученные рассмотрением пифагоровых троек $(3,4,5),(7,24,25):$

(0,±100), (±100,0), (±60,±80), (±80,±60), (±28,±96), (±96,±28).

Всего $20$ векторов.

Фигура составленная из векторов обязана быть замкнутой и выпуклой.

1.: Замкнутость: Сумма векторов сторон должна быть нулевой:
$n ∑ (xi,yi)=(0,0) i=1$
2.: Выпуклость: При обходе против часовой стрелки угол каждого вектора с начальным должен строго возрастать.

Из полученных условий имеем ограничения на $n.$ Из условия на углы получаем, что каждый вектор используется в качестве стороны не более одного раза $=⇒ n ≤20.$

Разделим полученные векторы на $4 :$

(0,±25), (±25,0), (±15,±20), (±20,±15), (±7,±24), (±24,±4).

Заметим, что у любого из данных векторов одна компоненты четна, вторая нечетна. Условие замкнутости поделим на $4,$ получим:

∑n (xi yi) i=1 4 ,4 =(0,0)

что не возможно при нечетном $n.$ Для все четных $4 ≤n ≤20$ построим искомый выпуклый многоугольник. Если $n$ делится на $4,$ то возьмем векторы с неотрицательными координатами, кроме $(100;0),$ “выстроим” их по возрастанию угла, это построит четверть фигуры, затем из четырех таких частей получим всю фигуру.

Если $n$ не делит на $4,$ построение такое: аналогично первому пункту встроим вектора, используя в начале $(100;0).$ Затем отразим все векторы, кроме $(100;0),$ относительно прямой $(y =50),$ а затем всю фигуру отразим относительно верхней границы.

Ответ:

При всех четных $4 ≤n ≤20$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#111175

Дан треугольник $ABC$ с вершинами в узлах целочисленной решётки и узлы $A′$ и $B′$ такие, что внутри отрезков $AB$ и $A′B ′$ поровну узлов. Докажите, что можно выбрать узел $′ C$ так, чтобы внутри треугольников $ABC$ и $′ ′′ AB C$ было поровну узлов.

Показать доказательство

Давайте нарежем решётку на прямые, параллельные сторонам $AB$ и $A ′B′.$ Тогда рассмотрим аффинное преобразование, которое переводит $AB$ в $′ ′ AB ,$ а прямые направления $AB$ в соответствующие прямые направления $′′ A B .$ Если допустим, что оба вектора $(AB$ и $′ ′ AB )$ не параллельны сторонам решётки, тогда нужно совместить $A$ и $′ A ,$ а потом посмотреть, на какое расстояние мы сместились по горизонтали из $A$ (в точку $A1),$ а потом, сколько шагов мы сделали по целым точкам вдоль вектора $AB$ и сделать аналогичные шаги. Если вектор горизонтальный, то идём сначала по вертикали. Тогда рассмотрим как точку $′ C$ образ точки $C.$ Получаем, что площади полученных треугольников совпадают, поскольку расстояние между прямыми уменьшилось в $AB-- A′B′$ раз, а основание увеличилось в $A′B′- AB$ раз. При этом все точки на сторонах исходного треугольника теперь на сторонах получившегося по построению (если есть точка на стороне, то можно провести через неё параллельную $AB$ прямую, которая аналогично перейдёт в параллельную $′ ′ A B)$ . Значит, по формуле Пика и количество внутренних узлов сохранилось, что и требовалось доказать.

Ошибка.
Попробуйте повторить позже

Задача 3#111177

В пространстве введена прямоугольная декартова система координат. Верно ли, что у любого прямоугольного параллелепипеда объема $2 1999,$ вершины которого расположены в точках с целыми координатами, ребра параллельны осям координат?

Показать ответ и решение

Пусть стороны данного параллелепипеда не параллельны осям, тогда они имеют длины вида $∘a2+-b2, i i$ откуда

2 2 2 2 2 2 4 4 2 2 (a1+b1)(a2+ b2)(a3 +b3)=1999 =⇒ 1999 = m +n , (m,n∈ ℕ)

Пусть $m,n$ не делятся на $1999,$ тогда из

2 2 1998 1998 m ≡1999 −n =⇒ m ≡1999 −n =⇒ 1 ≡1999 −1

получаем противоречие с малой теоремой Ферма. Поделим тождество на $19992,$ получим

(-n-)2 +(-m--)2 = 19992, 1999 1999

аналогично заключаем, что $m,n$ делятся на $19992 =⇒$

2 2 4 n +m ≥ 2⋅1999

— противоречие.

Ответ:

Верно

Ошибка.
Попробуйте повторить позже

Задача 4#111179

Докажите, что для любого $n$ существует окружность, внутри которой лежит ровно $n$ целочисленных точек.

Показать доказательство

Докажем сначала, что на окружности с центром $A =(√2,1∕3)$ не может лежать более одной целочисленной точки. Если $m$ и $n$ — целые числа, то

( √ -)2 ( 1)2 √- m − 2 + n − 3 = q− 2m 2

где $q ∈ℚ.$ Поэтому из равенства

( ) ( ) (m1 − √2)2 + n1 − 1 2 = (m2− √2)2+ n2− 1 2 3 3

следует, что $m1 =m2.$ По теореме Виета сумма корней уравнения $( 1)2 n − 3 = d$ равна $2∕3,$ поэтому лишь один корень может быть целочисленным. Расположим теперь радиусы окружностей с центром $A,$ проходящих через целочисленные точки, в порядке возрастания: $R1 <R2 < R3 < ....$ Если $Rn < R< Rn+1,$ то внутри окружности радиуса $R$ с центром $A$ лежит ровно $n$ целочисленных точек.

Ошибка.
Попробуйте повторить позже

Задача 5#111183

В парке, имеющем форму круга радиуса $R$ с центром в начале координат, деревья радиуса $r$ посажены во всех вершинах квадратной сетки со стороной $1,$ кроме центра. Пусть $2 l$ — минимальное целое число, не меньшее $2 R ,$ представимое в виде суммы квадратов двух целых взаимно-простых чисел. Докажите, что вид из центра полностью заслонен тогда и только тогда, когда $r≥ 1∕l.$

Показать доказательство

Докажем, что при $r <1∕l$ обзор не будет заслонен. Для этого достаточно предъявить точку вне круга, видимую из центра.

Пусть $2 2 2 l = a + b,$ покажем, что точку $P$ с координатами $(a,b)$ видно из центра. Пусть это не так, тогда существует точка $Q = (c,d)$ такая, что $ρ(Q,OP) <1∕l,$ где $ρ(A,BC)$ — расстояние от точки $A$ до прямой $BC.$

|bc− ad| 1 2 ρ(Q,OP)< 1∕l⇔ √a2+-b2 < l ⇔ (bc− ad) < 1

Последнее равенство может быть выполнено, если $bc= ad,$ но в таком случае, так как $Н ОД(a,b)= 1,$ то $a|c$ и $b|d,$ в таком случае $c2+ d2 > R,$ то есть такая точка $Q$ вне парка — противоречие.

Теперь покажем, что при $r≥ 1l$ все целые точки на решётке будут не видны. Будем считать $r< 1$ (иначе уменьшим радиус, а если $l= 1,$ то задача не имеет смысла). Тогда покажем, что можно считать, что $R = l− 𝜀.$ Будем расширять радиус, возможно, к нам добавятся какие-то новые точки $B$ , но тогда их координаты будут не взаимно просты, значит, найдётся точка $A$ внутри круга, координаты которой будут пропорциональны координатам $B.$ Но тогда если до какой-то прямой $OP$ $ρ(B,OP)≤ r,$ то и $ρ(A,OP)≤ r,$ то есть если в новом круге найдётся подходящая точка, то и в исходном тоже была. Теперь внутри нашего круга лежат все точки, расстояние до которых от начала координат меньше $R.$ Пусть есть точка $P,$ которую видно из начала координат. Рассмотрим прямоугольник со сторонами $2r$ и $2l$ c центром в $O,$ и сторона $2R$ которого параллельна $OP.$ Тогда прямоугольник центрально-симметричный, замкнутый и имеет площадь хотя бы $4.$ Тогда по теореме Минковского в нём есть целая точка. Ясно, что расстояние от этой целой точки до прямой $OP ≤r,$ если эта точка оказалась не в той полуплоскости, то рассмотрим симметричную ей. Итак, мы нашли в прямоугольнике точку, расстояние от которой до луча $OP ≤ r.$ Тогда посмотрим, что это могла быть за точка. Самая далёкая от $O$ — это вершина прямоугольника. Она находится на расстоянии $√l2+-r2.$ Поскольку $r< 1$ и сумма квадратов координат целая, эта точка $X$ или на расстоянии $l$ или внутри круга. Если она внутри круга, то мы уже победили, так что предположим, что она на расстоянии $l.$ Тогда покажем, что вся окружность точки $X$ радиуса $r$ уже закрыта. Рассмотрим какой-нибудь треугольник $OXA,$ где $A$ лежит в круге (для начала, например, $(1,0)).$ Допустим, этот треугольник оказался простым, то есть не содержит целых точек на сторонах и внутри. Тогда его площадь $1, 2$ а с другой стороны она $lh, 2$ где $h$ — расстояние от $A$ до $OP.$ Тогда $h = 1≤ r, l$ то есть дерево как минимум касается прямой $OX.$ Если же треугольник оказался не простым, то рассмотрим в нём ближайшую к $O$ точку $B$ и заменим $A$ на неё. Точка $B$ точно внутри круга (по определению $l$ ), площадь треугольника строго уменьшилась. Так мы найдём точки в обеих полуплоскостях относительно $OX,$ деревья которых как минимум касаются $OX.$ Заметим, что эти две окружности вместе целиком перекрывают окружность точки $X,$ так что если точка $X$ закрывала обзор для $OP,$ то найдётся и точка в круге, которая закроет обзор, что и требовалось доказать.

Ошибка.
Попробуйте повторить позже

Задача 6#111637

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри него лежит $n$ узлов решетки, а на границе $m$ узлов. Докажите, что его площадь равна $m- n + 2 − 1.$

Показать доказательство

Каждому многоугольнику $M$ с вершинами в узлах целочисленной решётки поставим в соответствие число $f(M) =∑ φi, i2π$ где суммирование ведётся по всем узлам решётки, принадлежащим $M,$ а $φi$ — угол, под которым виден многоугольник $M$ из соответствующего узла. Например, для внутренней точки $φi = 2π,$ для точки на границе (не являющейся вершиной) $φi =π.$ А сумма углов по вершинам многоугольника — это $(количество углов− 2)⋅π,$ тогда легко видеть, что:

2π (m − 2)π m f(M )= n⋅2π + --2π---=n + 2-− 1

Остаётся проверить, что $f(M )$ совпадает с площадью $S.$ Если многоугольник $M$ разрезан на части $M1$ и $M2$ с вершинами в узлах решётки, то $f(M )=f(M1)+ f(M2 ),$ так как углы в узлах складываются. Следовательно, если формула верна для $M1$ и $M2,$ она верна и для $M.$

Рассмотрим прямоугольник со сторонами $p$ и $q,$ параллельными осям решётки. Внутренних узлов: $(p − 1)(q− 1),$ граничных узлов: $2(p+q)− 4.$ Тогда:

f(M)= (p− 1)(q− 1)+ 2(p-+q)− 1= pq− p − q+ 1+ p+ q− 1 =pq 2

Формула верна для прямоугольников. Разрежем прямоугольник диагональю на два треугольника. Для каждого треугольника $f(M )= pq2 ,$ что совпадает с его площадью.

Любой многоугольник можно триангулировать непересекающимися диагоналями. Поскольку формула аддитивна и верна для треугольников, она верна и для всего многоугольника. Таким образом, $S =n + m2 − 1.$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#116310

На прямой отмечены $n$ точек. Какое наибольшее количество различных отрезков с обоими концами в отмеченных точках можно взять так, чтобы у любых двух отрезков, один из которых содержится в другом, был общий конец?

Показать ответ и решение

Оценка. Сдвинем точки так, чтобы они имели целые координаты от 1 до $n$ и отметим для каждого отрезка его середину. Заметим, что если у двух отрезков совпадают середины, то один из них целиком содержится в другом. Поэтому количество отрезков не превосходит количества отмеченных середин. Каждая середина имеет координату вида $k∕2$ , где $k ∈ℕ$ . Всего таких точек будет как раз $2n− 3.$

Пример. Отметим все отрезки длины 1 и длины 2.

Ответ:

$2n− 3$

Ошибка.
Попробуйте повторить позже

Задача 8#118082

Целые точки оси $OX$ раскрашены в два цвета. Докажите, что найдутся три точки одного цвета, одна из которых лежит посередине между двумя другими.

Показать доказательство

Предположим, что это утверждение неверно. Если цвета чередуются (то есть за каждой точкой первого цвета идет точка второго цвета и наоборот), то мы очевидно получим противоречие. Тогда можно полагать, что найдутся две точки одного цвета идущие подряд. Пусть точки раскрашены в красный и синий цвета. На самом деле можно заметить, что среди любых пяти подряд идущих точек найдутся две точки одного цвета (иначе мы получим противоречие, как и раньше). Рассмотрим больше, чем $5 2$ групп из пяти точек. Тогда среди них найдутся две одинаково раскрашенные группы. Рассмотрим эти две группы. В них выделим подгруппу из трех точек, где первые две подряд идущие одного цвета. Без ограничения общности можно считать, что это красная и две синие точки после нее. Аналогичную конструкцию можно найти во втором блоке. Пусть $d$ — расстояние между этими блоками из трех чисел. Отступим от правого блока еще вправо на $d.$ Первая точка нового блока из трех чисел не может быть красной (так как тогда найдется арифметическая прогрессия из трех красных точек, первые две из которых являются первыми точками ранее выделенных групп из трех чисел). Теперь заметим, что выбрав третью точку (синюю) первой группы, вторую точку (синюю) второй группы и первую точку новой выделенной группы получим арифметическую прогрессию. Значит, первая точка третьей группы не может быть и синей. Таким образом, она не может быть ни синей, ни красной — противоречие.

Ошибка.
Попробуйте повторить позже

Задача 9#118089

Целые точки плоскости раскрашены в два цвета. Докажите, что найдется равнобедренный прямоугольный треугольник с катетами, параллельными линиям сетки, с вершинами одного цвета.

Показать доказательство

Выберем прямоугольный треугольник, катеты, которого параллельны координатным осям, при этом катет, параллельный оси $X,$ направлен в противоположную сторону от нее (вектора катетов выходят из вершины прямого угла). Найдем треугольник, гомотетичный данному, подходящий под условие.

Предположим, что треугольника, гомотетичного данному, удовлетворяющего условию задачи, нет. Можно считать, что у данного треугольника две красных вершины и одна синяя. Рассмотрим прямую, проходящую через катет одноцветных вершин. Предположим, что найдется такой же треугольник с двумя красными вершинами на этой же прямой. Продолжим катет одного из этих треугольников и гипотенузу второго до пересечения. С одной стороны, точка пересечения должна быть синей, так как она является вершиной треугольника, гомотетичного исходному, с двумя красными вершинами. По аналогичной причине (так как у двух выбранных ранее треугольников есть по синей вершине), новая точка должна быть красной. Противоречие.

Покажем, что подходящие два прямоугольных треугольника на одной прямой найдутся. Рассмотрим девять троек подряд идущих точек на произвольной прямой, параллельной оси $oX.$ Очевидно, что раскраски двух таких троек будут одинаковыми. В первой тройке найдутся две точки одного цвета, тогда и во второй тоже, причем на таком же расстоянии, как в первой тройке. Применяя рассуждение, приведенное выше, мы получим противоречие.

Ошибка.
Попробуйте повторить позже

Задача 10#118092

Целые точки плоскости раскрашены в три цвета. Докажите, что найдется равнобедренный прямоугольный треугольник с катетами, параллельными линиям сетки, с вершинами одного цвета.

Показать доказательство

Предположим, что треугольника, гомотетичного данному, удовлетворяющего условию задачи, нет. Рассмотрим кадрат $4× 4.$ Всего существует $16 3$ вариантов его раскраски. Тогда выберем произвольную прямую, параллельную оси $oX,$ и рассмотрим $16 3 + 1$ квадратов $4× 4,$ у которых одна из сторон на этой прямой. Очевидно, найдутся два квадрата, раскрашенных одинаково.

На нижней стороне квадратов найдутся две точки, раскрашенные одинаково (пусть красные), находящиеся в квадратах на одном расстоянии. В этих же квадратах можно выделить равнобедренные прямоугольные треугольники с катетом — отрезком между красными точками. Верхние вершины этих треугольников одного цвета (пусть синего). Продлим гипотенузу одного и катет другого треугольника так, чтобы получился новый равнобедренный треугольник. Верхняя вершина нового большого прямоугольного треугольника должна быть зеленой (она вершина равнобедренных треугольников, у которых катеты с красными и с синими вершинами).

Теперь остается продублировать всю эту конструкцию еще раз. Для этого рассмотрим квадрат со стороной $(316+1)⋅4= t.$ Рассмотрим $3t+ 1$ таких квадратов. Два таких квадрата будут раскрашены одинаково. В первом квадрате на нижней стороне найдутся два квадрата $4× 4,$ раскрашенных одинаково, тогда и во втором большом квадрате найдутся два таких же квадрата. Таким образом, конструкция, описанная выше, может быть найдена в обоих квадратах, то есть мы нашли в каждом квадрате прямоугольные треугольники, гомотетичные данному, у которых на нижнем катете красные вершины, при этом на его сторонах параллельно оси $oX$ найдутся синие вершины, а последние вершины этих прямоугольных треугольников зеленые. При этом внутри больших квадратов все расстояния между описанными точками одинаковы. Рассмотрим найденные большие прямоугольные треугольники и продлим гипотенузу одного и катет второго до пересечения так, чтобы образовался новый прямоугольный треугольник, один из катетов которого содержит стороны двух рассматриваемых. Тогда одна из вершин этого треугольника не может быть раскрашена ни в один цвет. Противоречие.

Ошибка.
Попробуйте повторить позже

Задача 11#118093

Целые точки плоскости раскрашены в $k$ цветов. Докажите, что найдется равнобедренный прямоугольный треугольник с катетами, параллельными линиям сетки, с вершинами одного цвета.

Показать доказательство

При $k= 1,$ очевидно: все точки одного цвета. Пусть $k≥ 2,$ будем доказывать от противного. Заметим, что среди любых $k +1$ точек найдутся две одноцветные (для определенности будем говорить, что они красного цвета). Рассмотрим две одноцветные точки, лежащие на одной горизонтальной прямой, и треугольник, образованный ими. Тогда третья вершина будет не красной, пусть синей. В любом квадрате размера $(k +1)× (k+ 1)$ найдётся равнобедренный треугольник, у которого вершины на горизонтальном катете одноцветны, а третья — другого цвета.

Теперь рассмотрим квадрат $(k+ 1)× (k+1).$ Точки внутри него индуцируют раскраску квадрата, и всего таких раскрасок $(k+1)2 k .$ Рассмотрим $(k+1)2 M2 = k + 1$ квадратов, лежащих на одной горизонтальной прямой (т.е. при горизонтальных сдвигах переходящих друг в друга). Найдутся два квадрата с одинаковой раскраской, тогда у них внутри найдутся два одинаковых треугольника. Посмотрим на узел в пересечении прямых гипотенузы первого и вертикального катета второго (см. рисунок).

$PIC$

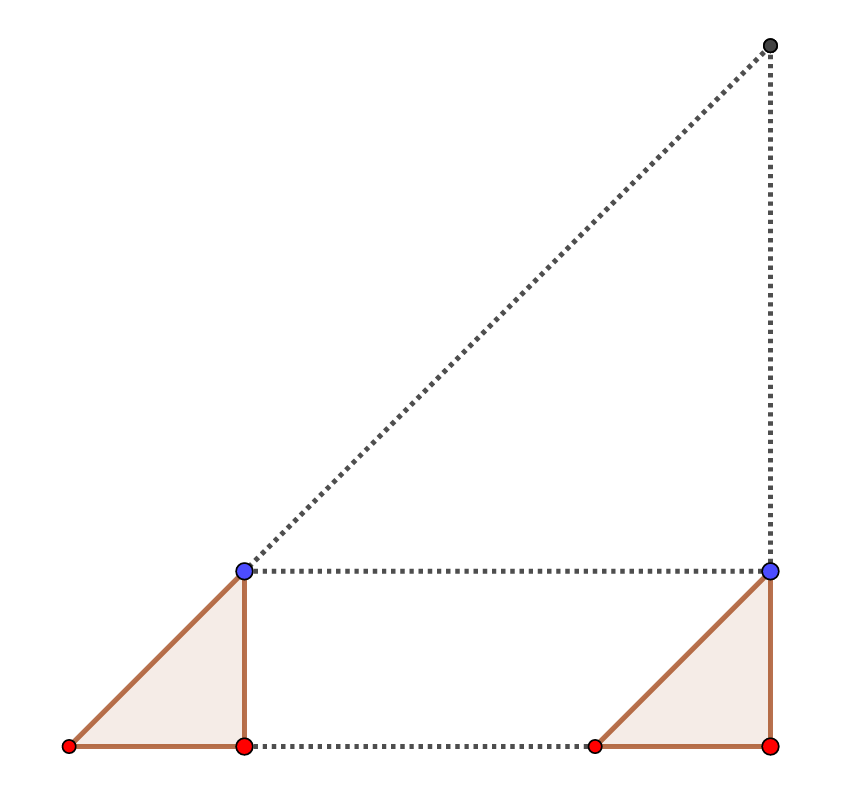
Вершина, отмеченная серым цветом на рисунке, не может быть синего или красного цвета. При $k= 2,$ мы бы уже получили противоречие. Заметим, что построенная конструкция находится в квадрате $M2 ×M2,$ и в любом квадрате такого размера такая конструкция найдется. Повторим построение: рассмотрим $kM22 +1$ квадратов размера $M2.$ Снова найдутся два с одинаковой раскраской и одинаковыми конструкциями внутри. Посмотрим на аналогичную точку пересечения: у неё теперь три запрета на возможные цвета. Размер стороны квадрата, в котором это содержится, обозначим $M3 = (kM22 + 1)M2.$ В любом квадрате со стороной $M3$ найдется конструкция, у верхней вершины которой (серой на рисунках для случаев двух и трёх цветов) будет $3$ запрета на цвет.

$PIC$

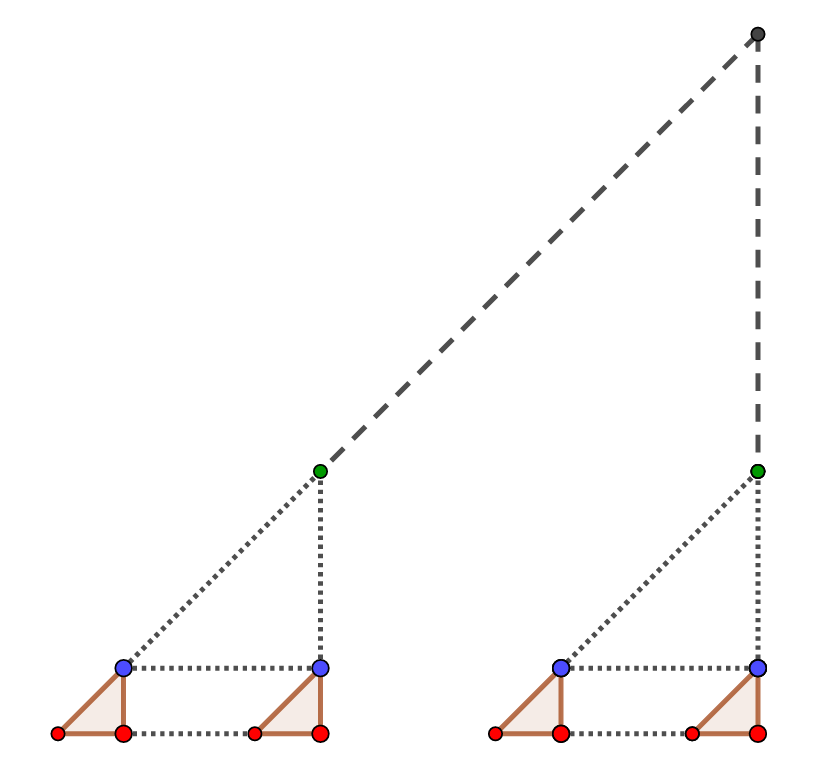
Обобщим рассуждения. Пусть $Mi$ — размер квадрата, в котором найдется индуктивно построенная конструкция, причём у верхней вершины будет $i$ запретов на цвет (так как есть $i$ пар точек, лежащих на одной горизонтальной прямой, причём одна из них лежит на гипотенузе, а другая — на вертикальном катете). Повторяя рассуждения для меньших случаев, в квадрате размера $Mi+1 =(kM2i + 1)Mi$ будет лежать конструкция с $i+ 1$ запретом на цвет верхней вершины. Тогда в квадрате со стороной $Mk$ все цвета будут запрещены, что приводит к противоречию.

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#119313

Докажите, что в выпуклом пятиугольнике можно выбрать три диагонали и сложить из них треугольник.

Показать доказательство

Рассмотрим пятиугольник $ABCDE$ и наибольшую диагональ в нем, не умаляя общности это $BE.$ Она разбивает пятиугольник на треугольник $ABE$ и четырехугольник $BCDE.$ В четырехугольнике $BCDE$ рассмотрим диагонали $BD$ и $CE.$ Проверим неравенство треугольника для треугольника на диагоналях $BE,BD$ и $CE.$ Получается, что $BD < BE +CE$ и $CE < BE +BD,$ так как $BE$ — наибольшая диагональ. Пересечение отрезков $BD$ и $CE$ обозначим за $F.$

Тогда образуется треугольник $BFE,$ откуда $BE < BF +EF < BD + EC,$ получаем, что из диагоналей $BE,BD, EC$ можно составить треугольник.

Ошибка.
Попробуйте повторить позже

Задача 13#119314

Квадрат со стороной $1$ покрыт несколькими меньшими квадратами со сторонами, параллельными его сторонам. Докажите, что среди них можно выбрать непересекающиеся квадраты, сумма площадей которых не меньше $1 9.$

Показать ответ и решение

Будем последовательно выбирать квадраты по следующему алгоритму: на каждом шаге берём квадрат наибольшей площади из оставшихся, удаляем его вместе со всеми пересекающимися квадратами. Полученные выбранные квадраты не пересекаются по построению.

Оценим суммарную площадь выбранных квадратов. Пусть на первом шаге выбран квадрат площади $S1.$ Все пересекающиеся с ним квадраты должны помещаться в квадрате со стороной $3a1$ (где $a1$ — сторона выбранного квадрата). Площадь этого большого квадрата $9S1,$ значит, суммарная площадь удалённых на первом шаге квадратов $≤9S1.$

Аналогично на каждом следующем шаге площадь удаляемых квадратов $≤9Sk.$ Поскольку весь исходный квадрат имеет площадь $1,$ получаем неравенство:

1 9(S1+S2 +...) ≥1⇒ S1+S2+ ...≥ 9

Таким образом, выбранные непересекающиеся квадраты дают требуемую оценку.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 14#119325

На окружности отметили $n$ точек. Оказалось, что среди треугольников с вершинами в этих точках ровно половина остроугольных. Найдите все значения $n,$ при которых это возможно.

Показать ответ и решение

Ключевое наблюдение: треугольник остроугольный тогда и только тогда, когда центр описанной окружности лежит внутри него. Рассмотрим произвольные четыре точки на окружности. В любом четырёхугольнике, вписанном в окружность, хотя бы два из четырёх треугольников будут тупоугольными. Действительно, если все четыре точки лежат на одной полуокружности, то все четыре треугольника тупоугольные. В противном случае, разбивая четырёхугольник диагональю, получим два треугольника, содержащих центр (острые) и два не содержащих (тупые).

Умножая количество четырёхугольников на $2,$ получаем нижнюю оценку общего числа тупоугольных треугольников:

2⋅C4n.

Каждый тупоугольный треугольник попадает ровно в $n − 3$ четырёхугольник. Следовательно, истинное количество тупоугольных треугольников хотя бы:

2⋅C4n n(n− 1)(n− 2) n−-3 =-----12-----

Сравнивая с общим числом треугольников $n(n−1)(n−2) C3n = ----6---,$ получаем, что доля тупоугольных не менее половины. Равенство возможно только, если в каждом четырёхугольнике ровно два тупоугольных треугольника, что достигается при $n =4, n = 5.$

Если четыре точки лежат на одной полуокружности, то любой треугольник из трёх таких точек будет содержаться в полуокружности, а значит, центр окружности не попадёт внутрь. Следовательно, все $4$ таких треугольника будут тупоугольными. Для $n> 5$ по принципу Дирихле обязательно найдётся четвёрка точек на одной полуокружности, что нарушит условие равенства половины.

$n =1,n= 2:$ треугольников нет.
$n =3 :$ треугольник один.
$n =4,$ пример на рисунке:
$n =5,$ подходит правильный пятиугольник.

Ответ:

$4,5$

Ошибка.
Попробуйте повторить позже

Задача 15#119327

На плоскости отмечены $n$ точек так, что никакие три из них не лежат на одной прямой. Докажите, что количество треугольников площади $1$ с вершинами в отмеченных точках, не превосходит $2 2 3(n − n).$

Показать доказательство

Рассмотрим все пары точек $A$ и $B.$ Для каждой пары найдём количество точек $C,$ таких что площадь треугольника $ABC$ равна $1.$ Площадь треугольника можно выразить как $1 2|AB |⋅h =1,$ где $h$ — высота к основанию $AB.$ Отсюда $-2-- h = |AB|.$

Для фиксированного отрезка $AB$ все подходящие точки $C$ должны лежать на двух прямых, параллельных $AB$ и отстоящих от него на расстояние $h.$ По условию на этих прямых не может быть трёх точек (иначе они коллинеарны), значит, на каждой прямой не более $2$ точек. Таким образом, для каждого $AB$ существует не более $2×2 =4$ точек $C.$

Общее количество пар точек: $2 n(n−1) Cn =--2--.$ Каждый треугольник учитывается трижды (по каждому из трёх оснований). Следовательно, общее число треугольников не превосходит:

n(n−1) 4⋅--2---= 2(n2− n) 3 3

Что и требовалось доказать.

Ошибка.
Попробуйте повторить позже

Задача 16#78087

На окружности расположено $20$ синих точек, а внутри окружности несколько красных таким образом, что никакие $3$ точки не лежат на одной прямой. Оказалось, что существует $1123$ треугольника с синими вершинами, содержащих ровно по $10$ красных точек. Докажите, что остальные $17$ треугольников с синими вершинами тоже содержат ровно по $10$ красных точек.

Показать доказательство

Прежде всего прокомментируем условие задачи. Количество треугольников с синими вершинами равно $C3 = 1140, 20$ поэтому “остальных” треугольников действительно $17.$

Выберем любой треугольник $T,$ для которого еще не известно, сколько в нем точек. Такие треугольники будем называть плохими. Заметим, что для любых четырех синих точек среди четырех треугольников, образованных тройками этих точек, не может ровно один быть плохим. Рассмотрим $17$ четверок синих точек, среди которых есть все вершины треугольника $T.$ Тогда для каждой такой четверки найдется плохой треугольник, отличный от $T.$ Но все эти плохие треугольники различны, что противоречит тому, что плохих треугольников не более $17.$ Значит, их нет вообще.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#79737

На плоскости дано множество из $n ≥9$ точек. Для любых $9$ его точек можно выбрать две окружности так, что все эти точки окажутся на выбранных окружностях. Докажите, что все $n$ точек лежат на двух окружностях.

Показать доказательство

Так как любые $9$ точек лежат на двух окружностях, то найдется окружность $O,$ на которой лежит не менее $5$ точек. Рассмотрим все точки множества, не лежащие на $O.$ Если таких точек четыре или меньше, то утверждение задачи верно. Действительно, дополнив их точками окружности $O$ до девяти, получим, что они лежат на двух окружностях, на одной из которых лежат три дополняющих точки, поэтому это $O.$ Значит, все наши точки лежат на другой окружности. Пусть вне окружности $O$ лежит не менее пяти точек. Возьмем пять точек $A1,...,A5$ на $O$ и три точки $B1,B2,B3$ вне $O.$ Через точки $B1,B2,B3$ проходит единственная окружность $O1.$ Возьмем точку $B,$ отличную от точек $A1,...,A5,B1,B2,B3.$ По условию существуют две окружности $′ O$ и $′ O 1,$ содержащие все точки $A1,A2,...,A5,B1,B2,B3,B.$ Тогда опять одна из окружностей $′ O$ и $′ O1$ совпадает с $O.$ Поскольку точки $B1,B2,B3$ не лежат на окружности $O,$ все они оказываются на той из окружностей $′ O$ или $′ O 1,$ которая не совпадает с $O,$ и эта вторая окружность тем самым совпадает с $O1.$ Получается, что точка $B$ лежит либо на $O,$ либо на $O1,$ что завершает доказательство.

Ошибка.
Попробуйте повторить позже

Задача 18#80769

Дан клетчатый прямоугольник $100×400$ . Сколькими способами можно закрасить 8 клеток этого прямоугольника так, чтобы закрашенное множество обладало хотя бы одной из следующих симметрий: относительно центра прямоугольника, относительно любой из двух "средних линий"прямоугольника ("средней линией"прямоутольника назовём отрезок, соединяющий середины двух его противоположных сторон). Ответ дайте в виде выражения, содержащего не более трёх членов (в них могут входить факториалы, биномиальные коэффициенты).

Источники: Физтех - 2024, 11.5 (см. olymp-online.mipt.ru)

Показать ответ и решение

Назовем восьмеркой набор из $8$ клеток. Пусть $A 1$ — множество восьмерок, симметричных относительной $l 1$ , $A 2$ — относительно $l 2$ , $B$ — относительно центра прямоугольника. $l1$ и $l2$ это средние линии прямоугольника.

Если выбрать какие-то $4$ точки в верхней половине прямоугольника, то остальные точки легко находятся в силу одной из рассматриваемой симметрий относительно $l1, l2$ и центра прямоугольника. Тогда количество элементов во множествах $A1, A2, B$ будет одинаковым. Тогда количество элементов в $A1$ будет равно количеству способов выбрать $4$ очки в одной половине фигуры относительно $l1.$ Остальные $4$ точки будут располагаются в другой половине. Тогда количество способов равняется $4 C100⋅200.$

Если восьмерка лежит сразу в $2$ из $3$ множеств $A1, A2, B,$ то она лежит и в третьей. Это значит, что пересечение двух множеств или пусто, или пересекается с третьим.

Чтобы найти ответ надо найти количество элементов в объединении множеств. Используя формулу включений-исключений, получаем, что

S = |A1∪ A2∪ B|= |A1|+|A2|+|B|− 2|A1∩ A2∩B |,

где $|M |$ — означает количество элементов во множестве $M,$ $S$ — искомое число

Если $2$ точки, лежащие в одной из четвертей прямоугольника, принадлежат пересечению всех $3$ множеств, то легко восстановить исходную восьмерку, удовлетворяющую сразу трем симметриям. Тогда можно посчитать количество элементов в пересечении множеств. Это будет количество способов выбрать $2$ точки в одной из четвертей прямоугольника, образованной $l1, l2$ и центром прямоугольника. Следовательно, количество элементов равняется $C2200⋅50.$

Тогда посчитаем $S$

S = |A1 ∪A2 ∪B|= |A1|+ |A2|+ |B|− 2|A1 ∩A2∩ B|=

= 3C420000− 2C210000

Ответ:

$3C4 − 2C2 20000 10000$

Ошибка.
Попробуйте повторить позже

Задача 19#80771

Даны 12 точек: 7 из них лежат на одной окружности в плоскости $α$ , а остальные 5 расположены вне плоскости $α$ . Известно, что если четыре точки из всех 12 лежат в одной плоскости, то эта плоскость — $α$ . Сколько существует выпуклых пирамид с вершинами в данных точках? (Пирамиды считаются различными, если их множества вершин различны.)

Источники: Физтех - 2024, 11.6 (см. olymp-online.mipt.ru)

Показать ответ и решение

Посчитаем отдельно количество тетраэдров и выпуклых $n−$ угольных пирамид с $n ≥4.$

Количество тетраэдров это количество способов выбрать $4$ точки, не лежащих одновременно в одной плоскости. Тогда количество тетраэдров равняется

4 4 C12− C 7 = 460

Найдем количество выпуклых $n−$ угольных пирамид с $n≥ 4.$ Основание такой пирамиды лежит в плоскости $α,$ а вершина — вне $α.$ Тогда посчитаем количество оснований. Надо просуммировать все способы выбрать от 4 до 7 вершин без учёта порядка

4 5 6 7 7⋅6⋅5 7⋅6 C 7 +C 7 +C 7 + C7 = 2⋅3 + 2 +7+ 1= 64

Для каждого из посчитанных оснований вершину пирамиды можно выбрать пятью способами, поэтому всего пирамид

5 ⋅64= 320

Итоговый ответ

460 +320= 780

Ответ: 780

Ошибка.
Попробуйте повторить позже

Задача 20#82622

В таблице $n ×m$ отметили $k$ клеток. Для какого наименьшего $k$ гарантированно можно выбрать $3$ отмеченные клетки, центры которых образуют прямоугольный треугольник?

Показать ответ и решение

Сначала покажем, что можно отметить не более $m +n − 2$ клетки так, чтобы никакие $3$ клетки не образовывали треугольник. Выберем в таблице центры всех клеток нижней строки и правого столбца, за исключением правой нижней угловой клетки. Всего выбрано $m +n − 2$ точки, и каждая тройка отмеченных точек образует тупоугольный треугольник.

Докажем, что больше $m + n− 2$ центров клеток выбрать нельзя. Для каждого отмеченного центра либо в его строке, либо в его столбце других отмеченных центров нет. Пометим этот ряд. Если помечены все строки, то выбрано всего не больше $m ≤ m +n − 2$ центров. Аналогична ситуация, когда помечены все столбцы.

Если же помечены не все строки и не все столбцы, то всего отмечено не более $m − 1$ строк и не более $n− 1$ столбцов: $(m − 1)+ (n − 1)= m +n − 2.$

Отсюда следует ответ $m + n− 1.$

Ответ:

$m + n− 1$

Следующая подтема