Истинные и ложные высказывания
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В ходе следствия каждый из них сделал по два заявления. Браун: «Я не делал этого. Джонс не делал этого». Смит: «Я не делал этого. Это сделал Браун.» Джонс: «Браун не делал этого. Это сделал Смит.» Потом оказалось, что один из них дважды сказал правду, другой — дважды солгал, третий — раз сказал правду, раз солгал. Кто совершил преступление?
Подсказка 1
Следует разобраться кто и сколько правдивых утверждений мог сказать, для этого можно рассмотреть несколько случаев.
Подсказка 2
Очень интересный случай : Браун отрицает совершение преступления им и Джонсом, мог ли он соврать?
Подсказка 3
Правильно! Браун не мог солгать дважды, иначе преступление совершили бы и Браун, и Джонс, что невозможно по условию задачи!
Подсказка 4
А если Браун не соврал совсем? Тогда Джонс тоже говорит только правду! А это противоречит условию задачи.
Подсказка 5
Единственный возможный случай - если Браун и лжет, и говорит правду, при разборе этого случая становится понятно, что Браун и есть преступник!
Предположим, что вор — Смит. Тогда Браун и Джонс оба сказали правду дважды. Противоречие. Предположим, что вор — Джонс. Тогда Браун и Смит один раз солгали и один раз сказали правду. Также получили противоречие. Если же вор — Браун, то тогда условие задачи выполняется. Других вариантов, очевидно, быть не может.
Браун
Ошибка.
Попробуйте повторить позже
Охотник Пулька для своей собаки Бульки заказал на АлиЭкспресс три куля собачьего корма. Наутро после доставки один куль оказался съеден. Под подозрение попали четверо, и Незнайке удалось установить следующее.
(1) Если алиби Пончика истинно, то Сиропчик также имеет алиби.
(2) Если Пончик ел корм, то либо Сиропчик, либо Авоська тоже ел корм (либо оба вместе).
(3) Из двух показаний: «Авоська ел корм», «Пончик не ел, но при этом ел Небоська» - хотя бы одно истинное.
(4) Если Небоська ел корм, то также ел либо Авоська, либо Сиропчик (либо оба вместе).
Кого из подозреваемых Незнайка может гарантированно обвинить в поедании за ночь целого куля собачьего корма?
Источники:
Подсказка 1
Начнём с рассмотрения третьего пункта. Условие на авоську мы никак не можем связать с другими фактами, так что давайте предположим, что Небоська ел, а Пончик нет. Тогда надо найти следствия этих фактов из других пунктов и сопоставить их друг с другом. Что мы можем сказать теперь?
Подсказка 2
Да, из 4 мы знаем, что вместе с Небоськой также ели Авоська и Сиропчик, но из 1 нам известно, что если Пончик не ел, то и Сиропчик тоже. Тогда получается, что первое условие из 3 в любом случае выполняется
Начнем с (3). Пусть Авоська не ел корм. Тогда Пончик не ел, а Небоська ел. Из (4) получаем, что либо Авоська ел, либо Сиропчик. При сделанном предположении это означает, что ел Сиропчик. Но из (1) следует, что Сиропчик не ел корм, т.к. Пончик не ел. Получено противоречие. Следовательно, Авоська виновен (корм ел).
Рассмотреть все варианты для трех оставшихся подозреваемых,
| Авоська | Небоська | Пончик | Сиропчик | ||
| 1 | ел | ел | ел | ел | |
| 2 | ел | ел | ел | нет | |
| 3 | ел | ел | нет | ел | невозможно в силу (1) |
| 4 | ел | ел | нет | нет | |
| 5 | ел | нет | ел | ел | |
| 6 | ел | нет | ел | нет | |
| 7 | ел | нет | нет | ел | невозможно в силу (1) |
| 8 | ел | нет | нет | нет | |
Видно, что каждый из подозреваемых мог как есть, так и не есть корм.
Ошибка.
Попробуйте повторить позже
В Летнюю школу приехали 54 человека. Какие из нижеуказанных утверждений обязательно верны?
(a) В каком-то из месяцев не меньше четырех именинников.
(b) В каком-то из месяцев от 1 до 5 именинников.
(c) Хотя бы в трех месяцах не больше, чем по 5 именинников.
(d) В каком-то месяце не меньше 6 именинников или в каких-то трех месяцах не меньше, чем по 5 именинников.
(e) Найдется семь месяцев, в которых в сумме не больше 31 именинника.
(f) Найдется семь месяцев, в которых в сумме не больше 29 именинников.
(a) Предположим, что во всех месяцах не более именинников. Тогда всего в летней школе не более
человек, хотя на самом
деле их
— противоречие. Значит, утверждение верно.
(b) Пусть все участники родились в январе, а в остальных месяцах именинников нет. Тогда есть месяца, в которых именинников, что
не подходит под условие. Утверждение неверно.
(c) Предположим, что не более, чем в двух месяцах не более именинников. Тогда в остальных
месяцах хотя бы по
именинников. Но тогда всего хотя бы
человек в летней школе, однако на самом деле их
— противоречие. Утверждение
верно.
(d) Построим отрицание: "во всех месяцах не более дней рождений и месяцев, в которых не менее
дней рождения, не более
двух". Тогда всего имеется не более двух месяцев, в которых дней рождения ровно
а в остальных не менее, чем
ти
месяцах не более
именинников. Тогда всего не более
человек в школе — противоречие. Утверждение
верно.
(f) Построим отрицание: "в любых семи месяцах в сумме хотя бы 30 именинников". Упорядочим месяца по возрастанию числа
именинников. Пусть в них именинников. Тогда из нашего отрицания получаем
Значит, хотя бы одно из чисел не менее
Значит, и все последующие не менее
следовательно
Тогда число именинников в сумме
Противоречие. Значит, исходное утверждение верно.
(e) В пункте (f) доказано, что найдётся семь месяцев с суммой именинников не больше 29. Эта же сумма не больше 31.
(a), (c), (d). (e), (f)
Ошибка.
Попробуйте повторить позже
Полиция задержала 50 человек, из которых 35 — преступники, которые говорят, что захотят, а 15 — свидетели, которые всегда говорят правду. Все задержанные знают, кто преступники. Какое наименьшее число человек достаточно выбрать, чтобы, спросив потом у каждого, кто именно преступники, по ответам вычислить хотя бы одного преступника?
Источники:
Подсказка 1
Полезная мысль: разбить людей на группы так, чтобы внутри каждой группы ответы были одинаковыми! При этом никто, разумеется, не назвал себя (иначе всё очевидно).
Подсказка 2
Допустим, мы опросили почти всех и взяли группу с минимальным количеством человек. Тогда, если в ней есть хотя бы 1 свидетель, свидетелями вместе с ним могут быть только люди из его группы и те, кого не опросили. А если это количество будет меньше 15, то мы сразу вычислим преступников...
Подсказка 3
Так же очевидно, что в каждой группе не более 15 человек, ведь каждый должен назвать 35 человек, и ни один из них не должен быть в этой группе. А как нам найти группу с минимальным количеством человек? Допустим, мы опросили n человек и поделили на х групп. Тогда 15х точно не меньше n. Воспользуемся принципом Дирихле, чтобы определить, сколько максимум человек может быть во всех группах! С помощью этого мы и сможем получить противоречие.
Пусть мы опросили людей. Опросим еще
случайных людей из оставшихся. Разобьем 46 опрошенных людей на 4 группы по
11,11,11,13 человек. Пусть групшы, где 11 человек, будут отвечать на вопросы так, будто свидетели они и 4 неопрошенных человека,
а группа из 13 человек будет отвечать на вопросы так, будто свидетели они и 2 любых неопрошенных. Так как мы не
можем понять, какая из версий настоящая, то и преступника мы найти не сможем, ведь любой человек в какой-то из версий
свидетель.
_________________________________________________________________________________________________________________________________________________________________________________
Выберем 47 человек и каждого спросим «Кто из жителей преступники?». Пусть каждый назвал 35 человек и никто не назвал себя, иначе преступник определяется очевидно. Разобьем всех людей на групшы так, что внутри одной группы ответы одинаковые.
Заметим, что в одной группе не больше 15 человек, иначе каждый из них обвинил бы менее 35 человек. Докажем, что найдется группа, в которой менее 12 человек.
Действительно, если в каждой группе хотя бы 12 человек, то если этих групп хотя бы 4 , то всего людей хотя бы , а если
групп не более, чем 3 , то всего людей не более, чем
— противоречие.
Возьмем ту группу, где меньше 12 человек. Если бы кто-то из них был свидетелем, то вместе с ним свидетелем могли быть только люди из его группы и неопрошенные люди, то есть менее 15 человек, противоречие. Значит, люди этой группы — преступники.
Ошибка.
Попробуйте повторить позже
После чемпионата мира по хоккею три журналиста написали статью о сборной Германии — каждый для своей газеты.
• Первый написал: «Сборная Германии за весь чемпионат забила больше но меньше
шайб».
• Второй: «Сборная Германии забила больше но меньше
шайб за весь чемпионат».
• Третий: «Сборная Германии забила нечётное количество шайб за весь чемпионат».
В итоге оказалось, что правы были только два журналиста. Сколько шайб могла забить сборная Германии на чемпионате? Укажите все возможные варианты через пробел в порядке возрастания.
Рассмотрим все возможные варианты.
Если шайб забито не больше 10 , то для нечётного количества шайб будет верно одно утверждение, а для чётного — ноль. Не подходит.
Если забито 11 шайб, то верны ровно два утверждения. Подходит.
Если шайб забито от 12 до 16 , то для нечётного количества шайб верны все три утверждения, а для чётного — два. Подходят только
чётные значения: .
Если забито 17 шайб, то верны ровно два утверждения. Подходит.
Если шайб забито не меньше 18, то для нечётного количества шайб верно одно утверждение, а для чётного — ноль. Не подходит.
Итак, нам подходят пять значений: .
Ошибка.
Попробуйте повторить позже
Маша опросила подружек из своего ансамбля и получила следующие ответы: 25 из них занимаются математикой, 30 были в Москве, 28 ездили на поезде. Среди ездивших на поезде 18 занимаются математикой и 17 были в Москве. 16 подружек занимаются математикой и были в Москве, притом среди них 15 еще и ездили на поезде. При этом в ансамбле всего 45 девочек. Возможно ли это?
Источники:
Посчитаем количество девочек, которые не были в Москве, не занимаются математикой, и не ездили на поезде. Получим
, чего быть не может.
Ошибка.
Попробуйте повторить позже
13 детей сели за круглый стол и договорились, что мальчики будут врать девочкам, а друг другу говорить правду, а девочки, наоборот, будут врать мальчикам, а друг другу говорить правду. Один из детей сказал своему правому соседу: «Большинство из нас мальчики». Тот сказал своему правому соседу: «Большинство из нас девочки», а он своему соседу справа: «Большинство из нас мальчики», а тот своему: «Большинство из нас девочки» и так далее, пока последний ребёнок не сказал первому: «Большинство из нас мальчики». Сколько мальчиков за столом?
Источники:
Понятно, что за столом были и мальчики, и девочки. Посмотрим, как сидели дети. За группой сидящих рядом мальчиков следует группа
девочек, затем снова мальчики, снова девочки и так далее (группа может состоять и их одного человека). Группы мальчиков и
девочек чередуются, поэтому их чётное число. Так как утверждений «большинство из нас мальчики» прозвучало семь, то
неверны шесть утверждений «большинство из нас девочки», и групп тоже было шесть. Чередование верных и неверных
утверждений означает, что в группах было по двое детей. Лишь сидящие рядом первый и последний ребёнок сказали одно и то
же, поэтому в их группе три человека. Это мальчики, так как их большинство. Всего за столом сидели
девочек и
мальчиков. На рисунке показано, как именно ребята сидели за столом. Первый говорящий обведён в
рамочку.
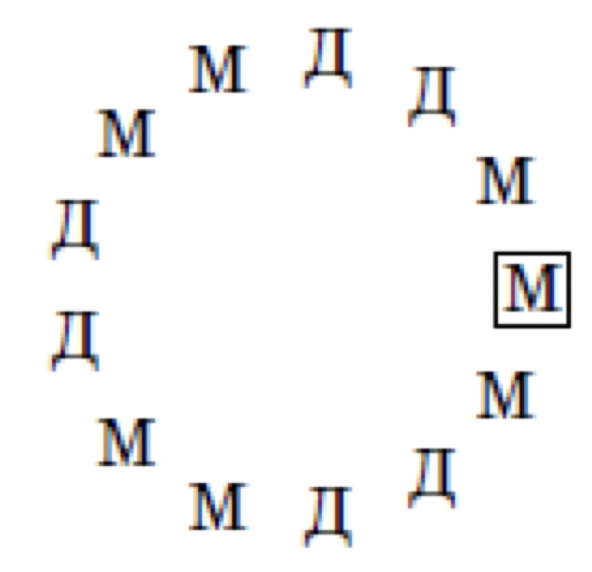
Ошибка.
Попробуйте повторить позже
Пусть — ненулевые числа. Докажите, что среди неравенств:
по крайней мере два — неверные.
Источники:
Подсказка 1
Очевидно, что среди наших трех чисел будут хотя бы 2 одного знака (пусть это х и у). Стоит попробовать поработать с ними. Принесет ли хоть одно неверное неравенство?
Подсказка 2
Из неравенств x+y>0 и x+2y<0 одно неверно. Получается, что либо у нас появятся неверные неравенств а такого же типа, либо же существует число, знак которого отличается от двух других (y и z). Как найти еще одно неверное неравенство?
Подсказка 3
Чтобы найти еще одно неравенство, нужно сравнить числа y + z и y + 2z.
Способ 1. Предположим противное. Среди трех ненулевых чисел найдутся два одного знака — пусть это и
Тогда одно из неравенств
и
неверно. Если все три числа имеют один знак, то мы таким образом найдем три неверных неравенства. В
противном случае среди трех пар
найдется пара, в которой первое число отрицательно, а второе положительно; пусть это
пара
Тогда одно из неравенств
и
также неверно, ибо
. Найденные нами неверные неравенства,
очевидно, различны.
Способ 2. Предположим, что верно хотя быть пять неравенств. Тогда верны все три неравенства из первых трех и хотя бы два из последних трех, или хотя бы два из первых трех и все три последних неравенства.
В первом случае, не ограничивая общности, считаем, что из последних трех верны четвертое и пятое неравенство. Но тогда
С другой стороны,
. Противоречие.
Во втором случае, не ограничивая общности, считаем, что Но тогда, как и и в первом случае,
Противоречие. Таким образом, из указанных неравенств хотя бы два неверные.
Ошибка.
Попробуйте повторить позже
Мальчики принесли в класс конфеты и раздали их девочкам. Петя сказал, что он принёс ровно половину общего числа конфет. Коля сказал, что он принёс ровно треть общего числа конфет, и отдал свои конфеты только Маше и Тане, причём Маше досталось на 3 конфеты больше, чем Тане. Докажите, что кто-то из ребят ошибся.
Источники:
Предположим, что оба мальчика не ошиблись. Поскольку Петя не ошибся, то общее количество принесённых конфет чётно (в два раза
больше количества конфет, принесённых Петей). Треть от чётного числа - тоже чётное число. Значит, количество конфет,
которые принёс Коля, чётно. Но, по его словам, он отдал девочкам нечётное количество конфет, так как количества конфет,
доставшихся Маше и Тане, имеют разную чётность (различаются на 3, а сумма двух чисел разной чётности нечётна. Получили
противоречие.
Ошибка.
Попробуйте повторить позже
Андрей, Максим, Игорь и Коля соревновались в велогонке. На вопрос, кто какое место занял, они ответили:
Андрей: — Я не был ни первым, ни последним.
Максим: — Я не был последним.
Игорь: — Я был первым.
Коля: — Я был последним.
Известно, что три мальчика ответили честно и только один соврал. Кто из мальчиков соврал?
Подсказка 1
Чтобы ответить на вопрос задачи, придётся рассмотреть все случаи: когда соврал Андрей, когда соврал Максим и т.д. Какой план действий в каждом из случаев?
Подсказка 2
В каждом из случаев берём отрицание высказывания мальчика, который соврал, и пытаемся найти противоречие с высказываниями других мальчиков!
Подсказка 3
Единственное — надо быть аккуратным с отрицанием высказывания и пользоваться законами логики, например, помнить, что отрицание союза «и» — это союз «или». Когда найдёте случай, в котором не будет противоречий, не забудьте привести пример!
- Пусть соврал Андрей. Тогда он первый или последний, но Игорь и Коля сказали правду — отсюда они занимают первое и последнее место, противоречие.
- Пусть соврал Максим. Отсюда он и Коля одновременно последние, снова противоречие.
- Пусть соврал Игорь, то есть он не первый. Тогда Коля последний, Андрей может быть вторым, а Максим — первым, отсюда Игорь — третий и все остальные сказали правду.
- Пусть соврал Коля, то есть он не последний. Но Максим и Андрей не последние, раз они сказали правду, а Игорь — первый, то есть последнее место никто не занимал, противоречие.
В итоге соврать мог только Игорь, в этом случае есть несколько распределений, в решении выше приведён пример одного из них.
Ошибка.
Попробуйте повторить позже
В комнате ламп. Петя сказал: «В этой комнате есть
включённых ламп». Вася ему ответил: «Ты не прав». И добавил: «В этой
комнате есть три выключенные лампы». Коля же сказал: «Включено чётное число ламп». Оказалось, что из четырёх сделанных
утверждений только одно верное. Сколько ламп включено?
Источники:
Подсказка 1
Давайте подумаем про высказывание №1 и №2, а также про высказывание №1 и №3 в совокупности. Что можно сказать про их истинность/ложность?
Подсказка 2
Верно, эти высказывания не могу быть одновременно верны или одновременно ложны! Тогда, какое из высказываний верное,
Подсказка 3
Конечно, высказывание №1 — единственное верное! Тогда, учитывая ложность высказывания №3 и №4, что можно сказать про количество включенных ламп?
Подсказка 4
Верно, включённых ламп не меньше 8 и при этом их нечетное количество!
Замечание.
Фраза “в комнате есть 5 ламп” не означает, что в комнате РОВНО 5 ламп. Она означает, что 5 ламп уж точно найдётся, в комнате их хотя бы 5.
_________________________________________________________________________________________________________________________________________________________________________________
Первое решение.
Заметим, что первое и второе высказывания не могут быть одновременно верны или одновременно неверны, потому что Вася отрицает
слова Пети — второе высказывание является отрицанием первого. Значит, ровно одно из этих высказываний истинно. По условию только
одно из четырёх высказываний истинно. Значит, третье и четвёртое заведомо ложны. Тогда с одной стороны включенных хотя бы (из
третьего высказывания), а с другой стороны включенных ламп нечётное число (из последнего высказывания). Под эти условия подходит
только число
_____________________________________________________________________________________
Второе решение.
Предположим, что верно утверждение Васи "Ты не прав". То есть это неправда, что в комнате есть включённых ламп. Но раз в
комнате меньше пяти включённых ламп, то тогда выключенных есть хотя бы
, а значит, и хотя бы
. Так что будут верны уже хотя бы
два утверждения, а по условию может быть только одно.
Значит, наше предположение неверно: Вася соврал, сказав "Ты не прав". Тогда Петя прав: в комнате хотя бы включённых ламп. И
раз утверждение Пети верно, то все остальные неверны. Значит, в комнате меньше
выключенных ламп и при этом их нечётное число.
Получаем, что в комнате одна выключенная лампа, а остальные
включены.
Ошибка.
Попробуйте повторить позже
В некоторой компании ни у каких двух сотрудников нет работы одинаковой сложности, и никакие двое не получают одинаковую зарплату. 1 апреля каждый сотрудник сделал два утверждения:
(a) Не найдется 12 сотрудников с более сложной работой.
(b) По меньшей мере 30 сотрудников имеют большую зарплату.
Сколько сотрудников в компании, если часть сотрудников дважды сказали правду, а остальные дважды солгали?
Источники:
Подсказка 1
Надо понимать, что под частью могут так же подразумевать всех или никого, когда все солгали или сказали правду, поэтому довольно разумно начать проверку условий с тривиальных случаев, когда все сотрудники солгали и все сказали правду.
Подсказка 2
Понятно, что такие случаи приводят к противоречию, а значит хотя бы 1 солгал и хотя бы 1 сказал правду. Часто бывает, что в задачах, в которых каждый элемент группы обладает количественным свойством, полезно взять самого сильного или самого слабого из них, потому что он потенциально несёт в себе намного больше полезной информации. А у нас как раз образовалось 2 группы: с правдивыми сотрудниками и лжецами.
Подсказка 3
Попробуйте порассуждать о самом богатом правдивом сотруднике и самом бедном лжеце. Нам хотелось бы как-то оценить кол-во каких-то сотрудников, очень удобно, что одна и та же фраза для лжеца и правдивого сотрудника даёт оценки сверху и снизу, поэтому в теории могла бы дать точное число каких-то сотрудников. (P.S. из численных данных о сотрудниках у нас есть только 2 числа, поэтому очень велика вероятность, что ответ - это сумма или разность этих чисел, что тоже стоит держать в уме при решении подобных задач, но это не означает, что так происходит всегда!)
Подсказка 4
Остаётся только провести аналогичные рассуждения о правдивом сотруднике с самой простой работой и для лжеца с самой трудной работе, и радоваться победе.
Если апреля все сотрудники компании сказали правду, то для сотрудника с наибольшей заработной платой второе утверждение будет
ложно, что быть не может. Если же все они солгали, то первое утверждение для сотрудника с наибольшой сложной работой будет верно,
то есть вновь получаем противоречие. Таким образом, существует хотя бы один солгавший и хотя бы один сказавший
правду.
Возьмем сотрудника, сказавшего правду с наибольшей зарплатой из всех правдивых сотрудников. Поскольку из его второго утверждения
следует, что по меньшей мере «лжецов» имеют большую зарплату, чем он. Второе утверждение солгавшего сотрудника, имеющего
наименьшую зарплату среди «лжецов» ложно, таким образом, не более
«лжецов» имеют большую зарплату и не более
«лжецов»
всего. То есть лжецов всего
Первое утверждение для «лжеца» с наиболее трудной работой среди всех «лжецов» ложно, поэтому существуют по меньшей мере
правдивых сотрудников, имеющих более трудную работу.
Первое утверждение для правдивого сотрудника с наименее сложной работой среди всех правдивых сотрудников верно, поэтому
существует не более правдивых сотрудников всего. То есть правдивых сотрудников ровно
Окончательно получаем, что в компании
работают
сотрудника.
Ошибка.
Попробуйте повторить позже
Есть комнат и
мальчиков, каждый из которых находится в одной из комнат. На двери каждой комнаты написано: “Тут ровно
один мальчик”. Назовём комнату нечётной, если в ней находится нечётное число мальчиков. Найдите количество нечётных комнат, если
известно, что среди надписей ровно четыре неверных.
Источники:
Из условия следует, что на комнатах надписи верны, т. е. там находится по одному мальчику. Все эти комнаты — нечётные. Допустим,
нечётна одна из четырёх комнат, надписи на которых неверны. Так как в этих четырёх комнатах находится четыре мальчика, и ровно один
мальчик ни в одной из них находиться не может, то в нечётной комнате находятся трое. Но тогда четвёртый находится в одной из
оставшихся комнат, и надпись на ней, вопреки нашему предположению, верна. Следовательно, все четыре оставшиеся комнаты —
чётные.
комнат
Ошибка.
Попробуйте повторить позже
В компьютерный класс привезли компьютеров, пронумерованных числами от
до
Некоторые компьютеры сломаны, поэтому
всегда дают неправильный ответ. Остальные исправны и дают правильный ответ. На всех компьютерах по очереди (от первого до
запустили программу, узнающую четность суммы цифр номера компьютера. Оказалось, что ответы компьютеров чередовались. Известно,
что исправных компьютеров все-таки больше. На сколько?
Источники:
Введем компьютер № который ответил не то, что компьютер №
(т. е. ответы по-прежнему чередуются). Заметим, что на отрезке
**
—**
и правильные ответы, и услышанные ответы чередуются. Поэтому на отрезке **
—**
все компьютеры одного типа (либо
все сломанные, либо все нормальные). На отрезке **
—**
**
—**
и т. д. аналогично. А вот переход с **
до **
правильный ответ одинаковый, а полученные ответы разные — поэтому на соседних участках компьютеры разные. Таким
образом, на отрезке **
одинаковое количество исправных и неисправных компьютеров (по
исправных и
неисправных). Остались компьютеры
Среди них
такого же типа, как и №
А вот
другого
типа. Поэтому среди
рассмотренных компьютеров типа “как №
” на
больше, чем типа “не как №
”. Значит, в
исходном наборе компьютеров типа “как №
” на
больше. Значит, первый компьютер — исправный, и исправных на
больше.
На один
Ошибка.
Попробуйте повторить позже
Некоторые продавцы умеют считать количество фруктов правильно, а остальные всегда ошибаются на Зато c полученными числами
вычисления проводят верно. Продавец Петя сказал: “Я могу разложить свои фрукты в пакеты ровно по три штуки”. Продавец Полина
возразила: “Но я посчитала, что апельсинов у тебя
А яблок —
” Продавец Петя ответил: “По два в пакет я их точно раскладывать
умею.” Сколько фруктов у продавца Пети?
Источники:
Из первых двух фраз ясно, что кто-то из продавцов ошибается. Если ошибается только Петя, то фруктов а по его подсчетам
или
но ни одно из этих чисел не делится на
Значит, ошибается Полина. Тогда фруктов
или
Если Петр тоже ошибается, то
по его подсчетам фруктов
или
Все эти числа нечетны, поэтому Петр не может ошибаться. Из чисел
только
последнее делится на
Ошибка.
Попробуйте повторить позже
В некоторой школе каждый десятиклассник либо всегда говорит правду, либо всегда лжёт. Директор вызвал к себе нескольких
десятиклассников и спросил каждого из них про каждого из остальных, правдивец тот или лжец. Всего было получено ответа
«правдивец» и
ответов «лжец». Сколько правдивых ответов мог получить директор?
Если возможны несколько ответов, вносите в ответ через пробел в порядке возрастания.
Источники:
Подсказка 1
Пупупу, каждый дал ответ про каждого другого… Попробуйте обозначить количество учеников и выразить через это число ответов!
Подсказка 2
Верно, если учеников n, то ответов — n*(n-1). Тогда количество учеников равно девяти! Тогда обозначьте количество учеников, которые всегда говорят правду и которые всегда говорят ложь — сколько и каких ответов в таком случае было получено от учеников?
Подсказка 3
Да, ответов «правдивец» было получено x*(x-1) — от учеников, которые всегда говорят правду и (9-x)*(8-x) — от учеников, которые всегда лгут! Осталось рассмотреть общее количество положительных ответов и найти x!
Подсказка 4
Если Вы сделали всё правильно, то x может быть равен либо 2, либо 7. Тогда, сколько было ответов «правдивец»?
Если учеников было , то они дали каждый по
-му ответу и всего получилось
ответ. Так как всего ответов было дано
,
то
. Пусть среди учеников было
честных и
лжецов. Тогда каждый из честных ребят дал
ответ
«правдивец» и
ответов «лжец». А каждый из лжецов дал
ответов «лжец» и
ответов «правдивец». Тогда
ответов «правдивец» всего было дано
, что по условию равно
. Отсюда получаем уравнение
. Приведя подобные слагаемые, получим:
. Это равенство раскладывается на множители
, то есть
может быть равен
или
. Подставляя полученные значения
в количество полученных
ответов «лжец» равное
, видим что
получится при обоих значениях
. Если честных было двое,
то они дали
правдивых ответов. Если же их было
, то тогда они дали
правдивых
ответов.
Ошибка.
Попробуйте повторить позже
Болельщики Спартака говорят правду, когда Спартак выигрывает, и лгут, когда он проигрывает. Аналогично ведут себя болельщики
Динамо, Зенита и Локомотива. После двух матчей с участием этих четырёх команд, каждая из которых закончилась победой одной из
команд, а не ничьёй, из болельщиков, смотревших трансляцию, на вопрос “болеете ли вы за Спартак?” положительно ответили человек,
на вопрос “болеете ли вы за Динамо?” положительно ответили
человек, на вопрос “болеете ли вы за Зенит?” положительно ответили
человек, на вопрос “болеете ли вы за Локомотив?” положительно ответили
человек. Сколько человек болело за каждую из
команд?
Подсказка 1
Стоит ввести обозначения и свести задачу на языку алгебры. Но ввести нужно не прям стандартно, ведь просто обозначения количеств команд нам ничего особо не даст (осознайте это).
Подсказка 2
Во-первых, 2 матча, 4 команды, значит, каждая сыграла по разу. Пусть команды A, B выиграли, а команды C, D — проиграли, где (А,B,C,D) — перестановка (Спартак, Динамо, Зенит, Локомотив). Маленькие буквы — количество людей в командах. Какой теперь вывод можно сделать из условия?
Подсказка 3:
На вопрос "Болеете ли вы за команду А?" ответили a + c + d человек. На вопрос "... за команду B?" ответили b + c + d человек. Осознайте аналогичный факт про команды C и D. Что теперь можно сказать?
Подсказка 4:
Если вы поняли, сколько человек ответили на вопросы про C и D, то поймёте, что за победителей болеет больше людей. Тогда кто победил, а кто проиграл?
Подсказка 5:
Верно! Локомотив и Зенит победили, а Спартак и Динамо проиграли. А вот теперь остаётся ввести самые стандартные обозначения из подсказки 1 и изящно дорешать задачу.
Так как в 2 матчах участвовали все 4 команды, то каждая команда сыграла по одному матчу. Если команда проиграла, то её болельщики
начинают врать и будут говорить, что болеют за другие команды, кроме своей. Пусть — болельщики команд, которые выиграли, а
— болельщики команд, которые проиграли. Тогда после игр на вопрос о команде
ответили, что болеют за неё те, кто действительно
болеют, и те, чья команда проиграла. За команду
— аналогично.
Получается, что за команду сказали, что болеют
человек, а за команду
болеют
. Так как болельщики
проигравших команд не могут сказать, что болеют за свою команду, потому что это будет правда, то за команду
будут болеть
человек,
а за команду
, наоборот, —
человек. Из этих соображений можно сказать точно, что
, следовательно, за
победителей будут болеть большее количество человек. Поэтому «Локомотив» и «Зенит» победили в своих играх, а «Спартак» и «Динамо»
проиграли.
Пусть тогда за «Локомотив» по-настоящему болеют человек, за «Зенит» —
, за «Спартак» —
, за «Динамо» —
. Получается,
что после опроса за «Локомотив» болеют
, за «Зенит» болеют
, за «Спартак» болеют
, а за «Динамо»
—
. Итого: болельщиков «Локомотива»
, болельщиков «Зенита»
, болельщиков «Спартака»
, болельщиков
«Динамо»
.
Ошибка.
Попробуйте повторить позже
C четверга по субботу гном ест на завтрак манную кашу, с воскресенья по вторник — рисовую кашу, а в среду делает себе яичницу. По
чётным числам месяца гном говорит правду, а по нечётным — неправду. В какие из первых десяти дней августа года он мог сказать:
«Завтра я буду есть на завтрак манную кашу»?
августа
года — четверг.
В ответ запишите в порядке возрастания возможные номера дней.
Рассмотрим случай, когда гном говорит правду: Так как четверг августа это нечетный день месяца, то в пятницу
августа гном не
соврет, что будет есть манную кашу. Так как в следующие дни у гнома нет в расписании манной каши, то правду он сказать не сможет до
августа, которое будет четвергом. Соответсвенно, гном не будет врать
и
числа.
Рассмотрим случай, когда гном врет: Гном может соврать и сказать, что будет есть манную кашу в понедельник, вторинк,
субботу и воскресенье. Если августа это четверг, то в субботу
августа гном может соврать и сказать, что будет есть
манную кашу. Значит и в понедельник он соврет, так как это будет
число месяца. Соответсвенно, гном соврет
и
числа.
Ошибка.
Попробуйте повторить позже
Три лисы: Алиса, Лариса и Инесса разговаривали на полянке. Лариса: «Алиса не самая хитрая». Алиса: «Я хитрее Ларисы». Инесса: «Алиса хитрее меня». Известно, что самая хитрая лиса солгала, остальные сказали правду. Какая лиса самая хитрая?
Алиса не может быть самой хитрой, т.к. если она сама хитрая, то она хитрее Ларисы, т.е. Алиса сказала правду. Но самая хитрая лиса должна была солгать.
Лариса тоже не может быть самой хитрой, т.к. она сказала правду про Алису, а самая хитрая лиса должна была солгать.
Поэтому остался только один вариант: самая хитрая — Инесса.
Ошибка.
Попробуйте повторить позже
Собираясь в школу, Миша нашел под подушкой, под диваном, на столе и под столом все необходимое: тетрадь, шпаргалку, плеер и кроссовки. Под столом он нашел не тетрадь и не плеер. Мишины шпаргалки никогда не валяются на полу. Плеера не оказалось ни на столе, ни под диваном. Что где лежало, если в каждом из мест находился только один предмет?
Источники:
По условию плеер нашелся не под столом, не на столе и не под диваном. Значит, плеер мог быть только под подушкой. Поэтому шпаргалка под подушкой лежать не могла. Но она не валялась и на полу (т. е. ее не было ни под столом, ни под диваном). Следовательно, шпаргалка лежала на столе. Тетрадь не лежала под столом, значит, ей осталось только место под диваном. Тогда под столом могли быть только кроссовки.
В итоге тетрадь была под диваном, шпаргалка — на столе, плеер — под подушкой, кроссовки — под столом.



