Тема Высшая проба

Планиметрия на Высшей пробе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела высшая проба

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80740

В выпуклом четырёхугольнике $ABCD$ выполнено $AB = BC = CD$ . Его диагонали $AC$ и $BD$ пересекаются в точке $E$ . Описанная окружность треугольника $ADE$ пересекает сторону $AB$ в точке $P ⁄= A$ и продолжение стороны $CD$ в точке $Q⁄= D$ . Найдите отношение отрезков $AP$ и $DQ$ .

Источники: Высшая проба - 2024, 11.3 (см. olymp.hse.ru)

Подсказки к задаче

Подсказка 1

Заметьте, что AP и QD – хорды окружности, описанной около треугольника AED. Значит, чтобы доказать, что они равны, нам требуется доказать, что на данные хорды опираются равные вписанные углы. То есть если мы докажем, что углы QAD и ADP равны, то решим задачу. Подумайте, при каком условии данные углы могут быть равны.

Подсказка 2

Обратите внимание, что углы QAD и ADP – накрест лежащие для прямых PD и AQ, а значит, если мы докажем параллельность данных прямых, то решим задачу.

Подсказка 3

В условии не просто так нам дали, что три стороны четырехугольника попарно равны. Давайте рассмотрим равнобедренные треугольники ABC и BCD, а конкретно, рассмотрим их равные углы при основаниях. Подумайте, как они могут помочь в доказательстве параллельности прямых PD и AQ.

Подсказка 4

Рассмотрим два соответственных угла AQD и PDC. Из вписанности четырехугольника AQDE следует равенство ∠AQD = ∠DEC. Обратите внимание, что DEC является внешним углом треугольника BCE, значит, он равен сумме углов EBC и ECB. Вспомним про равнобедренные треугольники: в них есть два равных угла ∠EBC = ∠BDC. Значит, для решения задачи остается доказать, что ∠PDB = ∠ECB. Подумайте, как в этом может помочь окружность.

Подсказка 5

Четырехугольник APDQ является вписанным, значит, углы PAE и PDE будут равными, а угол PAE будет равен углу BCA, так как это углы при основании равнобедренного треугольника.

Показать доказательство

Первое решение.

Из вписанности четырехугольника $APED$ следует, $∠P AE = ∠EDP$ . Треугольник $ABC$ является равнобедренным, а значит $∠BAC =∠BCA$ , следовательно, $∠BCA = ∠BDP$ .

Из равнобедренности треугольника следует, что $∠DBC = ∠CDB$ .

$PIC$

Наконец, в силу вписанности четырехугольника $AEDQ$

∠PDC = ∠PDB + ∠BDC = ∠BCE + ∠DBC = ∠CED =∠AQD

Второе решение.

Достаточно показать, что хорды $AP$ и $QD$ стягивают равные дуги в окружности $(AED )$ , то есть доказать равенство $∠P EA =∠QED$ . По теореме о внешнем угле верно, $∠P EA =∠BP E − ∠P AE.$

Поскольку треугольник $ABC$ является равнобедренным $∠BAE = ∠BCE$ , а из вписанности четырехугольника $AP ED$ следует, что $∠BP E =∠EDA$ . Таким образом,

∠PEA = ∠BP E− ∠PAE = ∠EDA − ∠BCE

Аналогично,

∠DEQ = ∠DAE − ∠EBC

$PIC$

Наконец, исходное равенство углов можно переписать в виде

∠EDA − ∠BCE = ∠DAE − ∠EBC

∠EDA +∠EBC =∠DAE +∠BCE,

что верно, так как суммой углов в каждой части равна углу между диагоналями четырехугольника.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#67769

В окружность $ω$ вписан треугольник $ABC$ такой, что $AB < BC.$ Биссектриса внешнего угла $B$ пересекает $ω$ в точке $M.$ Прямая, параллельная $BM,$ пересекает стороны $BC,$ $AB$ и продолжение стороны $CA$ за точку $A$ в точках $P,Q$ и $R$ соответственно. Прямая $MR$ вторично пересекает $ω$ в точке $X.$ Докажите, что точки $B,P,Q,X$ лежат на одной окружности.

Источники: Высшая проба - 2023, 11.4 (см. olymp.hse.ru)

Подсказки к задаче

Подсказка 1

Нам надо как-то воспользоваться тем, что BM паралельна PR. Например, можно перекинуть уголочек BMX на XRP как накрест лежащий. Куда ещё его можно перекинуть?

Подсказка 2

Т.к. BMX и BCX опираются на дугу BX мы получаем, что BMX=BCX. Не видно ли на картинке ещё одного вписанного четырехугольника?

Подсказка 3

Посмотрим на четырехугольник RXPC: XRP=XRQ=BMX=BCX=PCX. Тогда XRP=PCX, откуда следует, что RXPC вписан в окружность. Надо попробовать поперекидывать уголки в нем...

Подсказка 4

Нам необходимо доказать, что BPQX- вписан. Через какое равенство углов нам удобнее всего это сделать, если мы уже видим две окружности?

Подсказка 5

Наверное, через углы XBQ и XPQ, т.к. XBQ=XBA, а XPQ=XPR. Попробуйте перекинуть XBA на описанной окружности треугольника ABC, а уголок XPR на описанной окружности четырехугольника RXPC и вы завершите решение

Показать доказательство

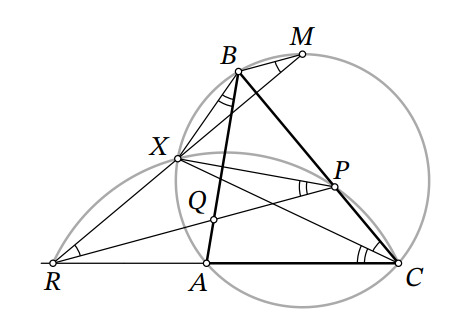
Докажем, что точки $R,X,P,C$ лежат на одной окружности $Ω,$ т.е. что четырёхугольник $RXP C$ является вписанным. Действительно, $∠XRP =∠BMX$ как накрест лежащие при параллельных прямых $BM$ и $RP$ и секущей $RM,$ а $∠BMX = ∠BCX$ как опирающиеся на одну дугу в $ω,$ значит, $∠XRP = ∠XCP.$ Следовательно, по признаку четырёхугольник $RXP C$ является вписанным.

Из этого получаем, что $∠XCA =∠XP R.$ Из окружности $ω$ получаем, что $∠XBQ = ∠XCA.$ Значит, $∠XBQ = ∠XP Q,$ а, следовательно, по признаку четырёхугольник $XBP Q$ является вписанным, т.е. точки $X,B,P,Q$ лежат на одной окружности.

Ошибка.
Попробуйте повторить позже

Задача 3#74780

Гипотенуза $AB$ прямоугольного треугольника $ABC$ касается вписанной и соответствующей вневписанной окружностей в точках $T ,T 1 2$ соответственно. Окружность, проходящая через середины сторон, касается этих же окружностей в точках $S1,S2$ соответственно. Докажите, что $∠S1CT1 = ∠S2CT2.$

Источники: Высшая проба - 2022, 11.3 (см. olymp.hse.ru)

Подсказки к задаче

Подсказка 1

Понятно, что скорее всего стандартный счёт углов тут не поможет. Здесь у нас и окружность Эйлера, и вписанная, и вневписанная. Так что либо нужны большие знания геометрических конструкций, либо какие-то хитрости. Пойдём хитрым путём. У нас есть как минимум три окружности на картинке, причём какие-то касающиеся. Какое преобразование плоскости тогда напрашивается сделать?

Подсказка 2

Верно, давайте сделаем инверсию с центром в точке C, причём сделать её с произвольным радиусом не слишком удобно. Давайте сделаем инверсию с радиусом √(ab/2), где переменные это стандартное обозначение сторон. Но если вы начнёте рисовать новую картинку, выйдет что-то не слишком хорошее. Какое ещё преобразование плоскости хорошо будет применить?

Подсказка 3

Смотрите, а давайте после инверсии сделаем ещё симметрию. Вот теперь осталось только понять, что и куда переходит после преобразований окончательно и почему мы выбрали такой радиус инверсии(на самом деле можно было без него, но так удобнее). В конце концов мы поймём, что углы переходят в друг друга, и победа!

Показать доказательство

Введём обозначения для длин сторон: $BC = a,AC = b,AB = c.$

$PIC$

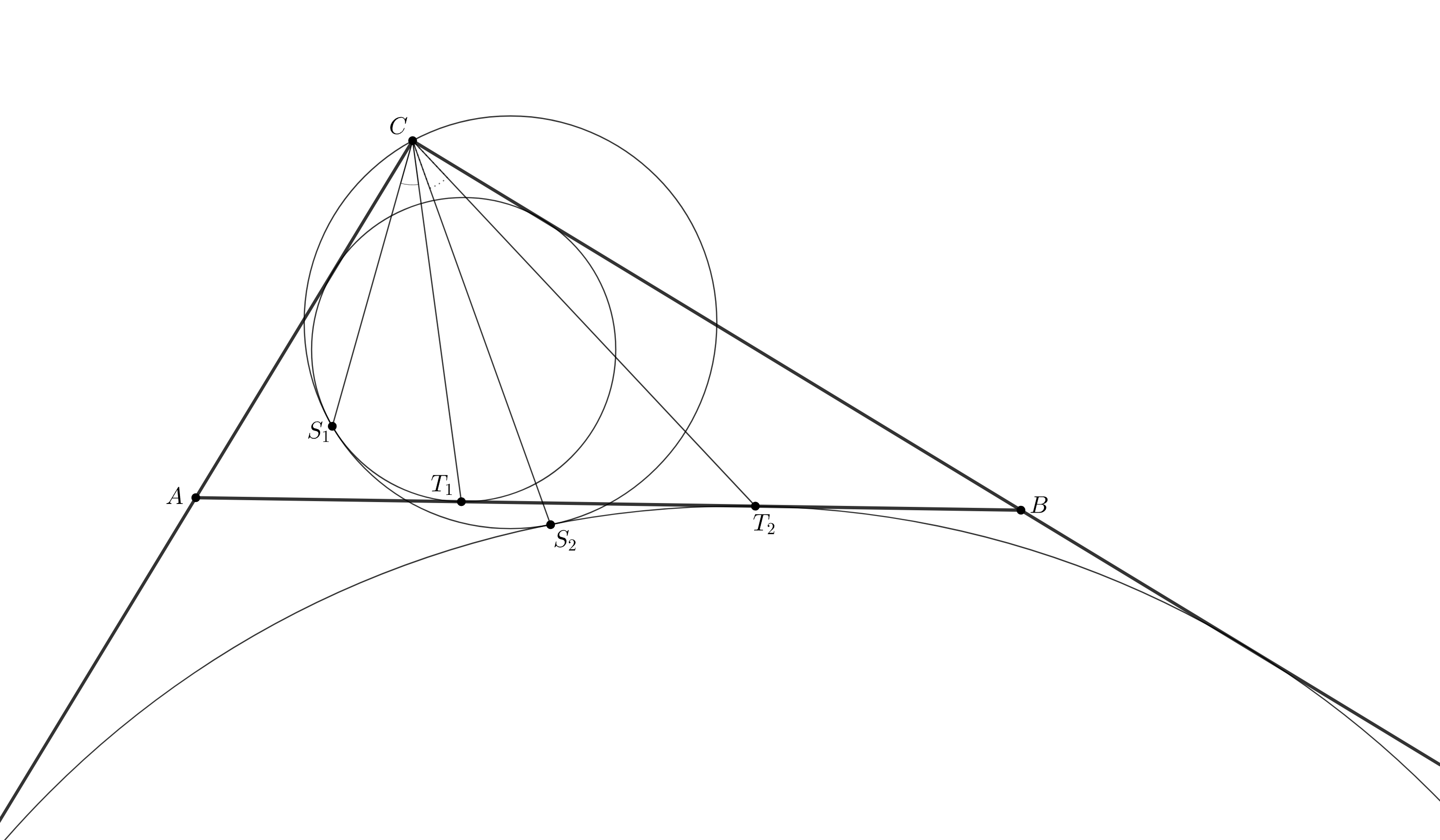
Сделаем инверсию с центром $C$ и радиусом $∘ --- R= 12ab$ с симметрией относительно биссектрисы угла $C.$

Середины сторон прямоугольного треугольника и вершина его прямого угла образуют прямоугольник, значит, все четыре на одной окружности. Значит, при инверсии образ окружности — прямая. Легко посчитать, что эта прямая отсекает от лучей $CA$ и $CB$ отрезки длины $a$ и $b$ соответственно, то есть симметрична $AB$ относительно биссектрисы угла $A.$ Поэтому гипотенуза и окружность Эйлера треугольника переходят друг в друга.

Касательная из $C$ к вписанной окружности равна её радиусу $r,$ а касательная из $C$ к вневписанной окружности равна полупериметру $p.$ Таким образом, их произведение $pr= S(ABC)$ — площади треугольника $ABC.$ Итак, $pr= R2.$ Поэтому вписанная и вневписанная окружности треугольника $ABC$ переходят друг в друга.

Следовательно, $T1$ переходит в $S2,$ а $T2$ переходит в $S1.$ Угол $∠S1CT1$ переходит в угол $∠S2CT2,$ значит, они равны.

Ошибка.
Попробуйте повторить позже

Задача 4#92421

В угол $AOC$ вписаны окружности $Ω 1$ и $Ω 2$ (радиус $Ω 1$ больше). $Ω 1$ касается сторон угла в точках $A$ и $B,$ а $Ω 2$ — в точках $D$ и $C$ соответственно. Точка $M$ — середина отрезка $BC.$ Прямые $MA$ и $MD$ вторично пересекают $Ω1$ и $Ω2$ соответственно в точках $X$ и $Y.$ Прямые $BX$ и $CY$ пересекаются в точке $Z$ . Докажите, что прямая $MZ$ проходит через середину отрезка $AD.$

Источники: Высшая проба - 2021, 11.4 (см. olymp.hse.ru)

Показать доказательство

$PIC$

Первое решение.

Докажем, что четырехугольник $ADXY$ вписанный. Для этого нам достаточно показать равенство $MA ⋅MX = MY ⋅MD$ . Для этого заметим, что эти произведения равны $MB2$ и $MC2$ соответственно (степень точки $M$ относительно окружностей $Ω1$ и $Ω2$ ).

Тогда получаем, что $∠DAX = ∠XY M,$ по свойству касательной $∠MBX = ∠MAB$ и $∠MY C = MCD$ из подобия соответствующих треугольников. Поскольку также равны углы $BAD$ и $DCO$ , то получаем, что сумма углов $XBC$ и $XY C$ равна $180∘.$

Тогда получаем вписанность $BXY C$ . Из этого получаем, что $ZX ⋅ZB = ZY ⋅ZC$ , что соответствует тому, что точка $Z$ лежит на радикальной оси окружностей $Ω1$ и $Ω2$ . Очевидно, что на ней же лежат точки $M$ и середина стороны $AD$ .

Второе решение.

Инверсия с центром $M$ и радиусом $MB$ переводит вписанную трапецию $ABCD$ во вписанный 4-угольник $XBCY$ . Тогда радикальные оси $BX$ и $CY$ пересекаются на радикальной оси окружностей $Ω1$ и $Ω2$ , которая проходит через середины $AD$ и $BC$ .

Ошибка.
Попробуйте повторить позже

Задача 5#75195

Дан описанный четырехугольник $ABCD,$ у которого радиусы вписанных окружностей треугольников $ABC$ и $ADC$ равны. Найдите угол между диагоналями $AC$ и $BD.$

Подсказки к задаче

Подсказка 1

Докажем, что точки касания вписанных окружностей треугольников и с диагональю совпадают. Как нам это поможет? А как это сделать?

Подсказка 2

Считать отрезки, на которые делит точка касания вписанной окружности сторону, мы умеем) Так посчитаем же их! А для чего дано условие об описанности четырехугольника?

Подсказка 3

Суммы противоположных сторон описанного четырехугольника равны! Теперь мы можем показать, что отрезки, на которые делят точки AC, равны!

Показать ответ и решение

Докажем, что точки касания вписанных окружностей треугольников $ABC$ и $ADC$ с диагональю $AC$ совпадают.

$PIC$

В самом деле, обозначим точки касания $TB$ и $TD$ соответственно. Тогда

|ATB|= |AB-|+|AC|−-|BC-||ATD|= |AD|+-|AC-|−-|DC-| 2 2

Критерий описанности четырехугольника

|AB|+ |CD |= |BC |+ |AD |

что равносильно равенству $|ATB|= |ATD |.$

Теперь легко видеть, что картинка однозначно задается радиусом вписанных окружностей треугольников $ABC$ и $ADC$ и расстояниями от точки касания до точек $A$ и $C.$ Значит, картинка переходит в себя при симметрии относительно прямой $AC,$ при этом точки $B$ и $D$ меняются местами. Но это означает, что $BD$ перпендикулярна $AC.$

Ответ:

$90∘$

Ошибка.
Попробуйте повторить позже

Задача 6#68267

Через вершины треугольника $ABC$ проведены три параллельные прямые $a,b,c$ соответственно, не параллельные сторонам треугольника. Пусть $A0,B0,C0$ — середины сторон $BC,CA,AB.$ Пусть $A1,B1,C1$ — точки пересечения пар прямых $a$ и $B0C0,b$ и $C0A0,c$ и $A0B0$ соответственно. Докажите, что прямые $A0A1,B0B1$ и $C0C1$ пересекаются в одной точке.

Источники: Высшая проба - 2019, 11.4 (см. olymp.hse.ru)

Подсказки к задаче

Подсказка 1

Какая теорема позволяет доказывать пересечение трёх прямых в одной точке? Если бы эти прямые были чевианами одного треугольника...

Подсказка 2

Обратная теорема Чевы! Нам нужно проверить выполнение условий этой теоремы для треугольника A₀B₀C₀. Тогда что можно сделать, чтобы найти отношения отрезков на сторонах этого треугольника?

Подсказка 3

Что-то не очень удобно искать эти отношения... А как можно перенести отношения отрезков на более удобную прямую?

Подсказка 4

Переносим отношения мы с помощью теоремы Фалеса, а перенести всё на прямую поможет ортогональная проекция на прямую, которая перпендикулярна нашим прямым a, b, c! Ведь в такой проекции середины сторон треугольника перейдут в середины отрезков!

Подсказка 5

Верно, можно ввести систему координат. Нужно только правильно выбрать оси, чтобы все нужные нам отрезки легко находились!

Показать доказательство

Заметим, что если доказать обратную теорему Чевы для треугольника $A B C 0 0 0$ (то есть равенство $B0A1⋅ C0B1⋅ A0C1 =1), A1C0 B1A0 C1B0$ то мы получим требуемое. Обозначим параллельные прямые через $a,b$ и $c.$

Давайте проведём прямую $d,$ перпендикулярную прямым $a,b,c$ и спроецируем ортогонально точки $A0,B0,C0,A1,B1,C1$ на неё. Нам это выгодно, потому что отношение, в которых делит точка отрезок при проектировании, как известно, сохраняется (это просто теорема Фалеса). Точки $A1,B1$ и $C1$ перейдут в $′ ′ A 1,B1$ и $′ C1.$

$PIC$

Введём декартову систему координат таким образом, что прямая $d$ — ось $y,$ а прямая $b$ — ось $x.$ Обозначим ординату $B′1$ через $β,$ а ординату $C′1$ через $γ.$ Точка $C0$ при проецировании переходит в точку $β C′0(0,2),$ точка $B0$ — в точку $γ B′0(0,2),$ точка $A0$ — в точку $A′0(0,β+2γ).$

Как мы знаем, отношения при проектировании сохраняются, а значит, нам достаточно доказать, что

′ ′ ′ ′ ′ ′ B-0A′-1′⋅ C0′B1′-⋅ A0′C1′= 1 A 1C 0 B1A0 C1B0

Нетрудно видеть, что длина любого отрезка из равенства равна модулю разности ординат его концов, поэтому его можно записать в таком виде:

|||γ2 β2 γ−β2-||| ||β⋅-γ−-β⋅-γ--||=1 2 2 2

Теперь видно, что всё сокращается, а значит, мы получили требуемое.

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#85485

Внутри выпуклого четырёхугольника $ABCD$ расположены четыре окружности одного радиуса так, что они имеют общую точку и каждая из них вписана в один из углов четырёхугольника. Докажите, что четырёхугольник $ABCD$ вписанный.

Источники: Высшая проба - 2017, 10.4(см. olymp.hse.ru)

Показать доказательство

Обозначим точку пересечения окружностей через $O$ , центры окружностей обозначим $A′,B′,C′,D′$ . Поскольку все четыре окружности имеют равный радиус, $′ ′ ′ ′ OA = OB = OC =OD$ .

Таким образом, $O$ является центром окружности, описанной вокруг $′ ′ ′ ′ A B C D$ . Значит, сумма противоположных углов в четырёхугольнике $′′ ′ A B C D$ равна $∘ 180$ .

$PIC$

Прямая $AB$ является общей касательной к паре пересекающихся окружностей равного радиуса с центрами в $A′$ и $B′$ , поэтому $AB ∥A′B ′$ . Аналогично параллельны остальные соответвующие пары сторон. Значит, в четырёхугольнике $ABCD$ суммы противоположных углов также равны $180∘$ , так что он также является вписанным.

Ошибка.
Попробуйте повторить позже

Задача 8#70311

В остроугольном треугольнике $ABC$ проведены высоты $AA ,BB ,CC 1 1 1$ . На стороне $AB$ выбрана точка $P$ так, что окружность, описанная около треугольника $PA1B1$ , касается стороны $AB$ . Найдите $PC1$ , если $PA = 30$ и $P B = 10$ .

Подсказки к задаче

Подсказка 1

Становится ясно, что нам придётся считать отрезки. По условию нам даны отрезки касательных, тогда какой прямой нам не хватает, чтобы воспользоваться известным равенством для окружности?

Подсказка 2

Нам необходима секущая! Давайте проведем ее через известные точки и начнём считать.

Подсказка 3

Проведите A₁B₁ до пересечения с AB в точке K и обозначьте KB = x. Что можно сказать про A₁B₁AB?

Подсказка 4

A₁B₁AB лежат на одной окружности, так что для них тоже можно воспользоваться равенством произведения отрезков секущих!

Подсказка 5

KA₁* KB₁ = KA * KB. KP² = KA₁* KB₁. Отсюда мы можем выразить x! Но ведь нам нужно было найти PC₁…было бы очень полезно найти еще одну окружность, в которой PC₁ был бы частью отрезка секущей.

Подсказка 6

Обратите внимание на окружность, проходящую через середины сторон и основания высот!

Показать ответ и решение

$PIC$

Продлим отрезки $AB$ и $B1A1$ до пересечения в точке $K$ и обозначим длину $KB = x$ .

Так как произведения отрезков секущих, проведенных из одной точки, равны: $KA1 ⋅KB1 = KA ⋅KB.$ А также квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки, поэтому $KP 2 = KA1 ⋅KB1.$ Следовательно $KP 2 = KA ⋅KB$ . Выразив эти отрезки через $x$ получим $x= 5$ и $KP = 15$ .

Отметим $M$ — середину стороны $BA$ . Основания высот $A1, B1, C1$ и точка $M$ лежат на одной окружности(Окружность девяти точек). Тогда $KC1⋅KM = KA1⋅KB1$ по свойству отрезков секущих, проведенных из одной точки $K$ .