Тема ПВГ (Покори Воробьёвы Горы)

Тождественные преобразования и функции на ПВГ

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела пвг (покори воробьёвы горы)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#85549

Найдите $f(2024)$ , если

f(x)=|2x− 1|− |2x− 3|+6 при x∈ [0;2]

и, кроме того, при всех целых значениях $x$ выполняются неравенства

f(x+ 3)≤ f(x)+ 6 и f(x+ 2)≥f(x)+ 4

Источники: ПВГ - 2024, 11.2 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Попробуем как-то связать два неравенства из условия. Какие аргументы для этого можно подставить?

Подсказка 2

Нужно подставить такое аргументы, чтобы числа в неравенствах могли получаться как с помощью +4, так и с помощью +6…

Подсказка 3

Попробуем поработать с f(x), f(x+3), f(x+6), а также с f(x+2), f(x+4). К каким неравенствам можно прийти? Какой вывод из этого сделать? Пробуем прийти к определенности, то есть к равенству!

Подсказка 4

f(x+6) <= f(x+3) + 6 <= f(x) + 12. Аналогично попробуем использовать и второе условие, к каким выводам придем?

Подсказка 5

f(x+3) = f(x) + 6, f(x+2) = f(x) + 4, f(x+1)=f(x)+2. А теперь попробуем задать функцию! ;)

Показать ответ и решение

Отметим, что $f(0)= 4,f(1)= 6,f(2)= 8$ . По условию, с одной стороны,

f(x+ 6)≤f(x+ 3)+6 ≤f(x)+12,

а, с другой стороны,

f(x+ 6)≥f(x+ 4)+4≥ f(x+ 2)+ 8≥ f(x)+ 12

Поэтому $f(x+ 6)=f(x)+ 12$ и, более того, все неравенства выше обращаются в равенства.

Поэтому $f(x+ 3)=f(x)+ 6,f(x+ 2)= f(x)+4$ и $f(x+ 1)= f(x)+2$ .

Таким образом, искомая функция - это функция $f(x)= 4+ 2x$ при целых значениях $x$ .

Кроме этого, известны значения функции на отрезке $[0;2]$ .

Значит, $f(2024)=4+ 2024⋅2 =4052$ .

Ответ: 4052

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#92993

Сравните числа $100-⋅ 102-⋅...⋅ 1020-⋅ 1022- 101 103 1021 1023$ и $5. 16$

Источники: ПВГ - 2022

Подсказки к задаче

Подсказка 1

Попробуем как-то телескопировать произведение в левой части неравенства. Для этого умножим его на число B = 101/102 × 103/104 × ... × 1023/1024. Пусть левая часть неравенства равна A. Можно ли сравнить A и B?

Подсказка 2

Конечно, n/(n+1) < (n+1)/(n+2), поэтому A < B! Теперь, зная число AB, можно ли доказать неравенство?

Показать доказательство

Заметим, что $-n-< n+1. n+1 n+2$ Поэтому

100 102 1020- 1022 A = 101 × 103 × ...× 1021 × 1023 <

101 103 1021 1023 < 102 × 104 × ...× 1022-× 1024-=B

Перемножив и сократив дроби, получим $( ) A ×B = 1100204 =22556 = 5162.$ С другой стороны, поскольку $A <B,$ то $( ) A2 < A× B = 516-2.$

Ошибка.
Попробуйте повторить позже

Задача 3#48745

Что больше: число $3∘5√13-+18− 3∘5-√13−-18-$ или наибольший корень уравнения $x2+$ $2020x− 6069 =0$ ?

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Мы можем просто найти второе число! Например, по теореме Виета можно найти наибольший корень этого квадратного уравнения.

Подсказка 2

Давайте обозначим первый страшный корень за а, а второй за б. Тогда заметим, что мы можем найти аб и а³-б³! А нам как раз надо найти а-б, а мы можем попробовать найти (а-б)³!

Подсказка 3

Если обозначить а-б за х, то мы можем получить кубическое уравнение, которое у вас получится решить и сравнить два числа!

Показать ответ и решение

Наибольший корень уравнения $x2+ 2020x− 6069= 0$ равен $3$ ( $− 2023+3 =− 2020,−2023⋅3= −6069 =⇒$ по обратной теореме Виета числа $3$ и $− 2023$ являются корнями уравнения $2 x +2020x − 6069= 0).$

Обозначим $∘3-√------ 3∘ -√------ a = 5 13+ 18,b= 5 13− 18.$

Отметим, что $3 3 3∘--√--2----2 3√------- a − b = 18− (−18)=36,a⋅b= (5 13) − 18 = 325− 324 =1.$ Тогда имеем:

(a− b)3 = a3− 3a2b+ 3ab2− b3 = (a3− b3)− 3ab(a− b)=36− 3(a − b)

Получается, что число $a− b$ является одним из корней уравнения

3 t = 36− 3t

которое равносильно

t3− 3t2+ 3t2− 9t+12t− 36 =0 ⇐ ⇒ (t− 3)(t2+ 3t+12)= 0

Так как $t2+3t+ 12= 0$ не имеет действительных корней, то единственным корнем уравнения является $t= 3.$

В итоге $a− b=3.$

Ответ:

ничего, эти числа равны

Ошибка.
Попробуйте повторить позже

Задача 4#47066

Определите значение функции:

5 4 3 2 f(x)=x + ax + bx + cx +dx+ e

в точке $x= 2018$ , если

f(2019)= f(2023)= 0, f(2020)=f(2022)= −3, f(2021)= −4.

Источники: ПВГ-2019, 11.5 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1!

Давайте попробуем сделать условие более симметричным - например, завести новую функцию g(x) = f(x + 2021)

Подсказка 2!

Наша цель - узнать что-то полезное про это равенство пятой степени. Для этого давайте попробуем сделать такую функцию, чтобы все наши значения были ее корнями.

Подсказка 3!

Например, подойдет m(x) = g(x) - x^2 + 4. Заметим, что теперь все наши числа из условия дают 0 этой функции. Осталось проанализировать получившееся!

Показать ответ и решение

Рассмотрим $g(x)= f(x +2021)$ . Тогда

5 4 3 2 g(x)= x +px + qx +vx + ux+ w,

при этом

g(−2)=g(2)= 0,g(−1)=g(1)=− 3,g(0) =− 4.

Рассмотрим $h(x) =g(x)− x2+ 4.$ Тогда

h(−2)= h(2) =0− 4+ 4= 0,h(−1)= h(1)= −3− 1+ 4= 0,h(0)=g(0)− 0+ 4= 0.

При этом $h(x)$ также остаётся многочленом пятой степени. Поэтому он имеет не больше пяти корней, при этом пять корней мы уже нашли, так что по теореме Безу $h(x)= x(x − 1)(x +1)(x − 2)(x +2).$

Искомое значение

f(2018)= f(− 3+2021)= g(−3)= h(− 3)+ (−3)2 − 4=

= −3⋅8⋅5+ 9− 4= −120+5 =− 115.

Ответ:

$− 115$

Ошибка.
Попробуйте повторить позже

Задача 5#65353

Найдите все возможные значения величины

-----f(t)−-f(0)----- T = f (t2)+f(t)− 2f(0)+ 2,

если $f(2x+ y)− f(x+ y)= 2x$ для всех действительных значений $x$ и $y.$

Источники: ПВГ-2019, 11.3 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Вначале забудем про T и попробуем решить фуру. Тут есть очень удобная подстановка, которая позволяет избавиться от одной из переменных. Какая?

Подсказка 2

Можно подставить y=-x, и тогда сразу находим функцию f(x)=2x+C.

Подсказка 3

Теперь подставляем в T и получаем выражение, значения которого можно исследовать с помощью производной.

Показать ответ и решение

Если подставить в функциональное равенство $y =− x$ , мы получим, что $f(x)− f(0)= 2x$ . Следовательно, числитель $T$ равен $2t.$

Если подставить $2 2 x= t,y = −t$ , мы получим, что $2 2 f(t )− f(0)=2t$ . Следовательно, знаменатель $T$ равен $2 2t+ 2t+2.$

Таким образом, $--t-- T = t2+t+1.$

С помощью производной или неравенства о средних можно выяснить, что:

при $1 --1-- 1 t> 0 1+ t+ t ≥ 3 =⇒ 0< T = 1+t+1t ≤ 3;$

при $t= 0 T =0;$

при $1 1 t< 0 1+ t+ t ≤ −1 =⇒ − 1≤ T = 1+t+-1t < 0.$

Ответ:

$[−1;1] 3$

Ошибка.
Попробуйте повторить позже

Задача 6#47065

Для функции $f(x) =− -x2-- 1+ x2$ найдите сумму

( -1-) (-1--) (1) f 2018 + f 2017 + ...+ f 2 + f(1)+ f(2)+ ...+f(2017)+ f(2018).

Источники: ПВГ-2018, 11.4 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1!

Попробуем сгруппировать слагаемые, каким образом это можно было бы сделать?

Подсказка 2!

Попробуйте сгруппировать f(x) + f(1/x) и посмотреть, что получится в их сумме!

Показать ответ и решение

Пусть $n ∈ℕ$ , тогда

( 1) n2 -12 n2 1 f(n)+ f n = − 1+n2-− 1n+-1-= −n2+-1 − n2+-1 =−1 n2

Отсюда вся сумма равна

S = (−1)⋅2017+ f(1)= − 4035 2

Ответ:

$− 4035 2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#75156

Решите уравнение

-----1------- ------1------ --------1-------- √x+-2+ √x+-3 + √x-+3-+√x-+4-+...+ √x+-2017+ √x-+2018 = 42

Подсказки к задаче

Подсказка 1

Первое, чего хочется при виде такого выражения, это как минимум избавиться от таких знаменателей. Каким самим простым приёмом это можно сделать?

Подсказка 2

Понятно, что от корней в знаменателе ничего хорошего не будет. То есть нужно, чтобы оба корня возвели в квадрат. Какой способ "легально" позволяет это сделать?

Подсказка 3

Да, конечно, нужно умножить на сопряженное число числитель и знаменатель. Тогда в знаменателе вовсе получится единица, а далее вся сумма хорошо сократится, и останется уравнение для корней, которое уже несложно решить. Можно два раза возвести в квадрат, либо же проделать снова умножение на сопряженное и воспользоваться монотонностью. Победа!

Показать ответ и решение

Избавимся от иррациональности в знаменателе каждого из слагаемых, домножив каждое из них на соответственное сопряжённое. Получим:

√x+-3− √x+-2 √x-+4− √x-+3 √x-+-2018− √x-+2017 (x-+3)−-(x+-2) + (x+-4)−-(x+-3)-+...+-(x+-2018)−-(x+2017)

Заметим, что в знаменателе в каждом слагаемом стоит $1,$ а большинство слагаемых в числителях входят с чередующимися знаками плюс и минус. Тогда после приведения подобных слагаемых в левой части наше уравнение превратится в:

√x-+-2018− √x+-2= 42

Снова домножим на сопряжённое к левой части, получим:

√------- √ ---- (x +2018)− (x+ 2)=2016= 42( x +2018+ x+ 2)

√------- √---- 48= x +2018+ x+ 2

В правой части находится монотонная функция, а значит она пересекает горизонтальную прямую $y = 48$ не более, чем в одной точке, заметим, что $x =7$ подходит, а, значит, и является единственным решением.

Ответ:

$7$

Ошибка.
Попробуйте повторить позже

Задача 8#58562

Найдите значение выражения

( --3-- --2-- --1--) --y2--- 2x− y − 2x+ y − 2x− 5y :4x2− y2

при

x= 4,y = 7 3 3

Источники: ПВГ-2016, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Не теряемся и приводим к общему знаменателю, объединяем нужное, сокращаем ненужное, а затем в уже красивое выражение подставляем значения!

Показать ответ и решение

Приведём к общему знаменателю в скобках, получим

4x2-− y2-3(2x+-y)(2x− 5y)−-2(2x−-y)(2x−-5y)−-(2x-+y)(2x−-y) y2 ⋅ (4x2− y2)(2x − 5y) =

2 2 2 2 2 2 = 12x-−-24xy− 15y-−28x-+-24xy− 10y-−-4x-+y-=− --24---= −24= 8 y (2x− 5y) 2x− 5y −9 3

Ответ:

$8 3$

Ошибка.
Попробуйте повторить позже

Задача 9#92005

Найдите минимальное значение выражения

∘ -----2---2 ∘ -2-------2 (x+ 6) + y + x + (y − 4)

при условии $2|x|+ 3|y|= 6$ .

Показать ответ и решение

Заметим, что выражение из условия есть сумма расстояний от точки с координатами $(x,y)$ до точек $(−6,0)$ и $(0,4)$ . А уравнение $2|x|+ 3|y|= 6$ задаёт ромб. Наша задача свелась к нахождению точки на границе ромба с минимальной суммой расстояний до двух выбранных. Докажем, что этот минимум достигается в точке, равноудаленной от точек $(−6,0)$ и $(0,4)$ .

Пусть точка $G$ лежит на прямой $l$ , параллельной $EF$ , и удаленной от прямой $EF$ на расстояние $h$ . Пусть также точка $H$ на прямой $l$ такова, что $EH =FH$ , а точка $P$ симметрична $F$ относительно прямой $l$ . Тогда получаем

EG + FG ≥EH + HP = EH + HF.

Причем равенство получается только, если точки $G$ и $H$ совпадают.

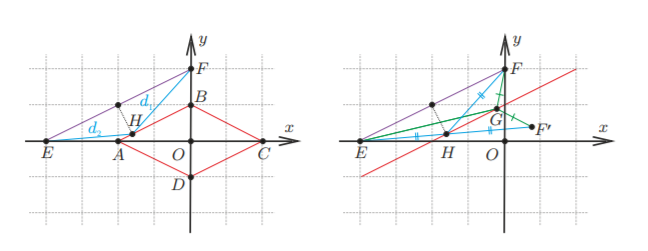
В нашем случае сторона ромба $AB$ параллельна $EF$ , а точка $H$ на прямой $AB$ , для которой $EH = FH$ , лежит на стороне ромба. Сумма расстояний от любой другой точки ромба до точек $E$ и $F$ больше $EH + FH$ . Остается найти $EF$ и расстояние между прямыми $EF$ и $AB$ . Применяя теорему Пифагора, получаем $√ ------ √-- EF = 16+36= 2 13$ . Расстояние между прямыми равно расстоянию от прямой $AB$ до начала координат, поэтому

h⋅AB = AO⋅BO,

откуда $h =√6-- 13$ .

Таким образом,

∘ 36---- ∘205 EH + FH =2 13 + 13= 2-13

Ответ:

$2∘ 205 13$

Ошибка.
Попробуйте повторить позже

Задача 10#48743

Сравните $∘|8√3−-16|− ∘8√3-+16$ и наименьший корень уравнения $4x2 +21x+ 17 =0.$

Источники: ПВГ-2015, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

А давайте найдём корни квадратного уравнения! Меньший из них равен -17/4. Попробуем найти, чему равно выражение слева!

Подсказка 2

Так, очень много корней… А давайте посмотрим на квадрат разности двух корней, что про него можно сказать?

Подсказка 3

Да, квадрат разности корней равен 16, тогда сама разность по модулю равна 4. А чему именно она равна?

Подсказка 4

Поскольку первый корень меньше второго, то само выражение отрицательно! Поэтому оно равно -4. Осталось только сравнить!

Показать ответ и решение

Квадратное уравнение имеет корни $− 1$ и $− 17 4$ (сумма этих двух чисел равна $− 21 4$ , а произведение $17 4$ , так что это корни по обратной теореме Виета).

Так как $8⋅8⋅3< 16⋅16(3< 2⋅2),$ то $√ - √- |8 3− 16|= 16 − 8 3.$ Это число меньше, чем $√- 16+ 8 3,$ поэтому $∘ -√------ ∘ -√----- √-- c= |8 3 − 16|− 8 3+ 16= − c2.$

Посчитаем квадрат разности корней

√- √- ∘ -----√-------√-- √ ------- c2 =16− 8 3+ 8 3+ 16− 2 (16 − 8 3)(16+ 8 3)= 32− 2 256− 192= 16

В итоге сама разность корней $c =−4$ и она больше, чем наименьший корень уравнения $17 − 4-$ .

Ответ:

$∘ |8√3-− 16|− ∘8-√3+-16$ больше, чем наименьший корень уравнения $4x2+ 21x +17= 0.$

Ошибка.
Попробуйте повторить позже

Задача 11#38689

Найдите множество значений выражения $x− y+ 1$ при условии

2 (x− y) = 2|2y− x|+ x+ 15.

Источники: ПВГ-2013, 11.4 (см. pvg.mk.ru)

Показать ответ и решение

Выполним замену переменных: $x− y+ 1= a,2y− x= t$ . Тогда условие задачи переформулируется следующим образом:

Найдите множество значений $a$ при условии $2 2|t|+ t=a − 4a− 12$ .

На плоскости переменных $(a,t)$ это условие задает множество, состоящее из частей парабол

1( 2 ) t= 3 a − 4a− 12

( ) t= − a2− 4a− 12

для значений $a∈ (−∞;−2]∪[6;+ ∞).$

Ответ:

$(−∞,− 2]∪ [6,+∞ )$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#68636

Найдите наименьшее значение выражения

( 1 1)2 (x y) x + y − 3⋅ y + x + (x+ y)2

при условии, что

1+ 1 =3. x y

Источники: ПВГ-2013 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Согласитесь, с дробями такого вида работать не очень удобно, да и вообще не особо понятно, что тут делать. Самый первый и очевидный шаг это привести всё к общему знаменателю.

Подсказка 2

Если всё правильно привести к общему знаменателю, то из условия мы можем найти, что x+y = 3xy. Что теперь хочется сделать с этим равенством?

Подсказка 3

Подставим в наше исследуемое выражение 3xy вместо x+y. Теперь мы получили многочлен, который зависит от переменной xy. Исследуйте его на минимальное значение и получите возможный ответ. Осталось проверить, что такие неизвестные-минимизаторы удовлетворяют заданному условию

Показать ответ и решение

Преобразуем выражение: $(x+y)2− 3⋅ (x+y)2−2xy+ (x+y)2 xy xy$ .

Из условия следует, что $x+ y = 3xy$ , подставляя, получим

(3xy)2 (3xy)2− 2xy -xy- − 3⋅----xy----+ (3xy)2 =9− 3⋅(9xy − 2)+ 9(xy)2 =9 ⋅(xy)2 − 27xy+ 15

Это квадратный трехчлен относительно $xy$ , принимает минимальное значение $− 5,25$ при $xy = 32$ . Можно показать, что такие $x,y$ существуют, решив соответствующую систему уравнений:

{ { 1x + 1y = 3 x+yx−y3xy = 0 xy = 32 ⇐⇒ xy = 32 ⇐⇒

⌊ { √-- { | x= 9+4√57 ⇐⇒ x+ y = 92 ⇐ ⇒ || { y = 9−4√57 xy = 32 |⌈ x= 9−4√57 y = 9+457

Ответ: -5,25

Предыдущий раздел

Следующий раздел