Инверсия + симметрия
Ошибка.
Попробуйте повторить позже
Дан треугольник Пусть
— его биссектриса,
— середина дуги
а
— проекиия ортоцентра на медиану, проведённую
из вершины
Окружность
пересекает прямую, проходящую через
и параллельную
в точке
Докажите, что
Источники:
Подсказка 1
Внимательно посмотрите на картинку и отметьте все (на ваш взгляд) необходимые точки пересечения. Как можно было бы доказать нужное равенство? Быть может, можно найти какую-то полезную фигуру? Интуитивно понятно, что нам нужны новые объекты - давайте их проводить!
Подсказка 2
Проведите окружности CPW и AHB и изучите их точки пересечения. Что можно сказать про связь точки P с ними?
Подсказка 3
Точка P — пересечение медианы с дугой окружности AHB.
Подсказка 4
Докажите, что середина дуги AHB лежит на окружности CPW. А что можно сказать про отрезок, соединяющий точки пересечения указанных окружностей?
Подсказка 5
Докажите параллельность отрезка, соединяющего точки пересечения окружностей (AHB) и (CPW), и отрезка CQ.
Первое решение. Известно, что точка — пересечение медианы с дугой
Пусть
— середина этой дуги, а
—
середина
Точки
и
симметричные
и
относительно
лежат на описанной окружности
поэтому
откуда заключаем, что принадлежит окружности
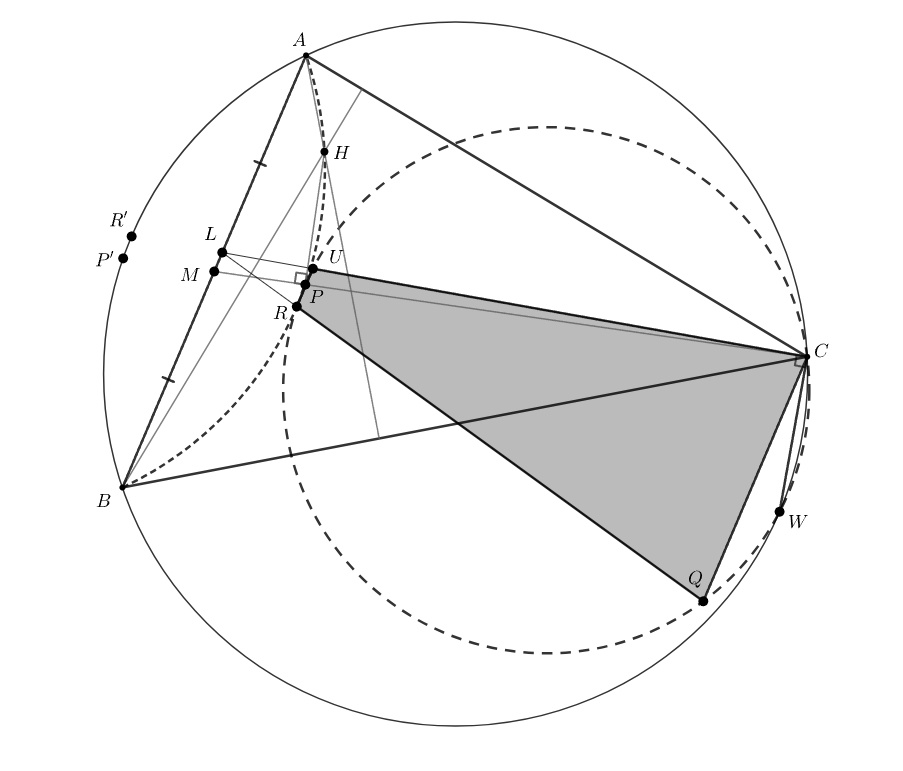
Далее, так как луч
пересекает окружность
в точке
диаметрально противоположной точке
следовательно,
Отсюда
— средняя линия треугольника
то есть
— середина отрезка
Во вписанной трапеции
общий серединный перпендикуляр к
и
проходит через
что и даёт требуемое.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Пусть — точка на прямой
такая, что
Докажем, что точки
лежат на одной
окружности.
Рассмотрим композицию инверсии с центром и симметрии относительно
которая взаимно обменяет вершины
и
Эта же
композиция меняет местами прямую
и описанную окружность треугольника, поэтому
переходит в середину
дуги
а
—
в основание
внешней биссектрисы угла
точка Шалтая
переходит в точку пересечения касательных к окружности
проведённых в
и
Прямая при этом перейдёт в касательную к окружности
в точке
а окружность с центром
проходящая через
перейдёт в серединный перпендикуляр к
(поскольку образы точек
и
инверсны относительно этой окружности). Следовательно,
переходит в точку пересечения касательных в
и
Эта точка, образ точки и точка
лежат на одной прямой — поляре точки
относительно окружности
что завершает
доказательство.
Ошибка.
Попробуйте повторить позже
Общие внешние касательные и
к окружностям
и
пересекаются в точке
Окружность
проходит через точку
касается окружностей
и
и повторно пересекает прямые
и
в точках
и
Касательные из точек
и
к
отличные от
и
пересекаются в точке
Касательные из точек
и
к
отличные от
и
пересекаются в точке
Докажите, что
Подсказка 1
Требуется доказать, что 2 направления изогональны в угле. Очень часто придумать синтетическое доказательство подобных фактов тяжело, поэтому попробуйте доказать, что sin∠AKD/sin∠AKB=sin∠CKB/sin∠CKD.
Подсказка 2
sin∠AKD/sin∠AKB=sin∠CKB/sin∠CKD = XD/XB*KB/KD, где X- точка пересечения диагоналей. На картинке есть полувписанная и полувневписанная окружности. Какие полезные точки можно на них отметить?
Подсказка 3
Нужно отметить точки касания описанной окружности BKD с s1 и s2, также стоит отметить точки касания окружностей со сторонами. Найдите на рисунке биссектрисы и запишите отношения. Как перекинуть отношения на сторону BD?
Подсказка 4
Рассмотрите композицию инверсии+симметрии в точке К. Тогда полувписанная окружность перейдут во вневписанную, также образуются подобия. Найдите их и покажите, что sin∠AKD/sin∠AKB = BT/TB, где Т - точка касания вневписанной окружности.
Первое решение. Не умаляя общности будем считать, что лежит внутри
а
— снаружи. Окружности
и
известны как полувписанная и полувневписанная окружности треугольника
Пусть
и
— их центры, и пусть
касается
и
в точках
и
а
— в точках
и
соответственно. Как известно, середина
— это центр
вписанной окружности треугольника
а середина
— центр
его вневписанной
окружности (касающейся отрезка
Пусть
и
— радиусы этих окружностей; из гомотетии в точке
получаем, что
.png)
Пусть и
пересекают
в точках
и
соответственно. Пусть
Тогда треугольники
и
подобны (их соответственные стороны параллельны), и коэффициент их подобия равен отношению высот из точек
и
, то есть
Отсюда
Значит, прямоугольные треугольники
и
также подобны, поэтому
.png)
Пусть и
касаются
в точках
и
соответственно. По теореме Ньютона, прямые
и
пересекаются в
одной точке, то есть
проходит через
Поскольку прямые
и
— поляры точек
и
относительно
точка
— полюс прямой
относительно
откуда
Аналогично получаем, что
Теперь из доказанного выше
вытекает, что
что равносильно требуемому.
.png)
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Как известно, направление луча из вершины угла однозначно задаётся отношением синусов углов, образованных им
со сторонами угла. Поэтому для решения задачи достаточно доказать, что Пусть
и
пересекаются в точке
Заметим, что
Пусть касается прямых
и
в точках
и
соответственно. Как известно, в описанном четырехугольнике
выполнено равенство
Пусть полувписанная окружность
касается
в точке
Еще один известный факт:
— биссектриса угла
а
— биссектриса угла
Отсюда получаем
и, следовательно,
Так как при композиции инверсии с центром в точке и симметрии относительно биссектрисы угла
меняющей местами точки
и
окружность
переходит во вневписанную окружность
треугольника
то точка
переходит при таком
преобразовании в точку касания
с отрезком
Обозначим эту точку через
Из вышесказанного следует, что треугольники
и
а также треугольники
и
подобны. Тогда
Рассуждая аналогично, получаем, что
где — точка касания вписанной окружности треугольника
с отрезком
Осталось заметить, что точки
и
симметричны относительно середины
откуда
Ошибка.
Попробуйте повторить позже
Пусть – описанная окружность треугольника
Окружность с центром в точке
касается отрезка
в точке
и дуги
окружности
не содержащей точку
в точке
Докажите, что, если
то
Сделаем симметрию относительно биссектрисы угла и инверсию с таким радиусом, чтобы
и
где звездочкой
обозначаем образ точки под действием композиции преобразований.
переходит в прямую
отрезок
переходит в дугу описанной окружности
Вторая окружность перейдет в окружность, касающуюся дуги
и отрезка
причем в силу
центр окружности все еще лежит на биссектрисе угла
Существует
единственная окружность с такими свойствами и центром на биссектрисе (это отдельное несложное упражнение), поэтому вторая
окружность переходит сама в себя. Точка
же переходит в точку касания отрезка
и окружности, то есть в точку
а
точка
– в точку
При этом
и
по определению симметричны относительно биссектрисы, значит
и
тоже.
Упражнение можно показать так: по мере продвижения точки от точки пересечения биссектрисы и
к точке пересечения
биссектрисы и дуги
расстояние от
до прямой
увеличивается, а от
до описанной окружности уменьшается (это расстояние
можно выразить как радиус
минус длина отрезка от
до центра
). А нас интересует такая точка
что расстояния от нее до
прямой
и до дуги
совпадают. Ясно, что такая точка уникальна.
Ошибка.
Попробуйте повторить позже
Дан треугольник Одна окружность проходит через точку
и касается прямой
в точке
а вторая проходит через точку
и касается прямой
в точке
Докажите, что вторая точка пересечения этих окружностей лежит на симедиане (прямой симметричной
медиане относительно биссектрисы треугольника) треугольника
Сделаем симметрию относительно биссектрисы угла и инверсию с таким радиусом, чтобы
и
где звездочкой
обозначаем образ точки под действием композиции преобразований. Две окружности, описанные в условии, перейдут в прямые
параллельные сторонам
и
через точку
будет проходить прямая, параллельная
и через точку
будет проходить прямая, параллельная
Вторая точка пересечения окружностей перейдет в точку пересечения прямых. Назовем
ее
а исходную точку пересечения окружностей соответственно
Итак,
– диагональ получившегося параллелограмма. Она,
разумеется, проходит через середину
Прямая
получилось симметрией прямой
относительно биссектрисы угла
но прямая
содержит медиану треугольника
Значит
действительно содержит симедиану треугольника
Ошибка.
Попробуйте повторить позже
Треугольник вписан в окружность с центром в точке
Биссектриса угла
пересекает сторону
треугольника в точке
Окружность
касается сторон
и
и внутренним образом касается описанной окружности треугольника
в точке
Вневписанная окружность, соответствующая вершине
касается стороны
в точке
а соответствующая вершине
касается
в точке
Прямые
и
пересекаются в точке
на окружности, описанной около треугольника
Докажите, что описанная
окружность треугольника
содержит точку
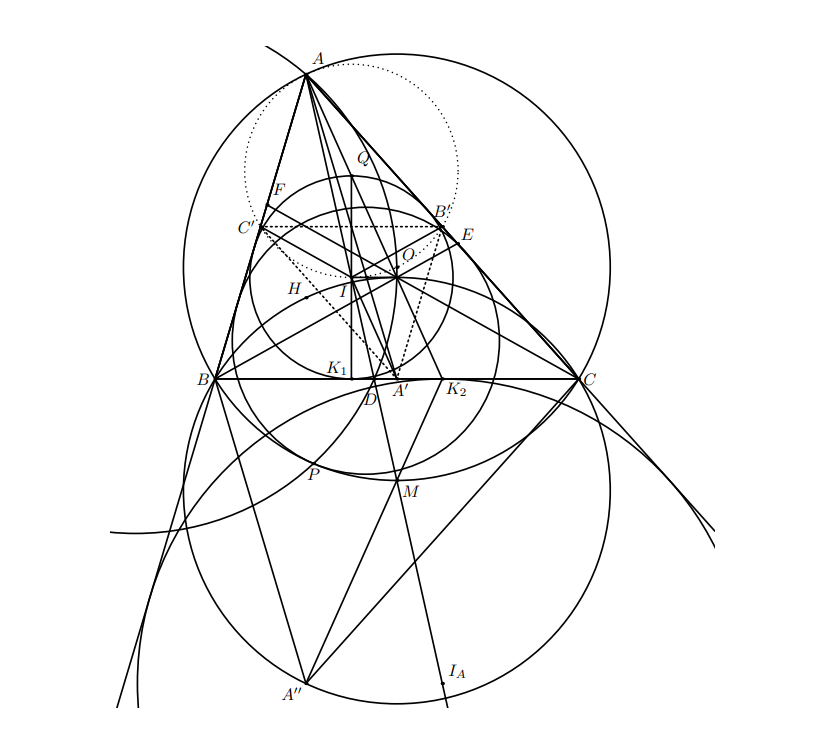
Точка – точка Нагеля треугольника
(точка пересечения трех прямых, соединяющих вершины треугольника с точками касания
противоположных сторон с соответствующими вневписанными окружностями; почему все три пересекаются в одной точке –
простое упражнение на теорему Чевы). Отметим
– ортоцентр треугольника
Так как
лежит на окружности
Так как
точка
лежит на описанной окружности треугольника
Пусть – серединный треугольник,
– центр масс (точка пересечения медиан) треугольника
– инцентр (центр
вписанной окружности)
Лемма. Точка является точкой Нагеля для треугольника
Доказательство. Пусть и
– точки касания вписанной и вневписанной окружностей со стороной
. Точка
–
диаметрально противоположная точке
. Поскольку гомотетия с центром в
переводит вписанную окружность во вневписанную, точку
в точку
Значит, точки
лежат на одной прямой. Точка
является серединой отрезка
а точка
– серединой
поэтому
параллельна
Треугольники
и
гомотетичны с центром в
и коэффициентом
прямые, соединяющие вершины треугольника с точками касания противоположных сторон с
соответствующими вневписанными окружностями, переходят в
Значит, точка
переходит в точку
и
является точкой Нагеля для треугольника
Дополнительно мы поняли, что
делить отрезок
в отношении
Гомотетия из доказательства леммы переводит точку в точку
Поскольку
лежат на одной окружности, то и их образы
лежат на одной окружности.
и
перпендикулярны сторонам
и
соответственно, поэтому
вписанный. Поскольку
биссектриса угла
дуги
и
равны, а значит
В силу гомотетичности,
и
является серединой дуги
описанной окружности треугольника
Отобразим точки и
относительно
Назовем образы
и
Поскольку описанная окружность треугольника
симметрична окружности
относительно
(следствие того факта, что
при симметрии попадает на
описанную окружность),
– середина дуги
окружности
Следовательно,
лежит на биссектрисе угла
Сделаем симметрию относительно биссектрисы угла и инверсию с таким радиусом, чтобы
и
где звездочкой
обозначаем образ точки под действием композиции преобразований. Точка
переходит в точку
так как описанная окружность
переходит в прямую
Точка
переходит в точку на прямой
которая в два раза ближе к
чем образ основания
высоты из
на
Но образ основания высоты это точка на окружности
значит образ
это
Вневписаная
окружность, соответствующая вершине
переходит в
значит
переходит в
Точки
лежат на одной
окружности так как прообразы
лежат на одной прямой.
так как
– центр окружности,
содержащей
и
так как
симметрична
относительно
Так как точка
лежит на серединном
перпендикуляре к
треугольники
и
равнобедренные и подобные (они имеют общий угол
).
Прямые
и
тем самым, антипараллельны для угла
значит
лежат на одной окружности.
Получается, что пять точек
лежат на одной окружности, и, в частности,
лежит на описанной окружности
Ошибка.
Попробуйте повторить позже
Даны сфера и фиксированная точка внутри нее. Через
проводятся три попарно перпендикулярные хорды
и
Пусть
и
— проекции
на плоскости
и
Доказать, что все прямые
проходят через одну
точку.
Подсказка 1
Задача легко переформулируется на плоскость. Попробуйте решить для начала эту задачу. Это может натолкнуть на верную мысль и помочь понять, как устроена картинка.
Подсказка 2
Попробуйте подступиться к задаче при помощи инверсии с центром в точке P. Где должна находиться точка пересечения прямых на новой картинке?
Подсказка 3
Рассмотрите расстояние от центра сферы до образов точек X и X’. Что вы можете сказать про них? Покажите, что образ центра сферы – середина отрезка, вершинами которого являются образы P и P’. Отсюда выведите утверждение задачи.
Пусть Выполним преобразование: инверсию относительно сферы
радиуса
с центром
и
затем центральную симметрию с центром
— так что
переходит в себя, а точки
и
и
и
меняются
местами. Точка
при инверсии переходит в точку сферы
диаметрально противоположную точке
то есть в
противоположную для
вершину параллелепипеда, построенного на векторах
Пусть это точка
тогда
Пусть аналогично точка
такова, что
Имеем (с учётом перпендикулярности
векторов
Здесь центр описанной сферы
с радиусом
Получаем, что
и аналогично
равны одной и той же величине
не зависяшей от тройки хорд.
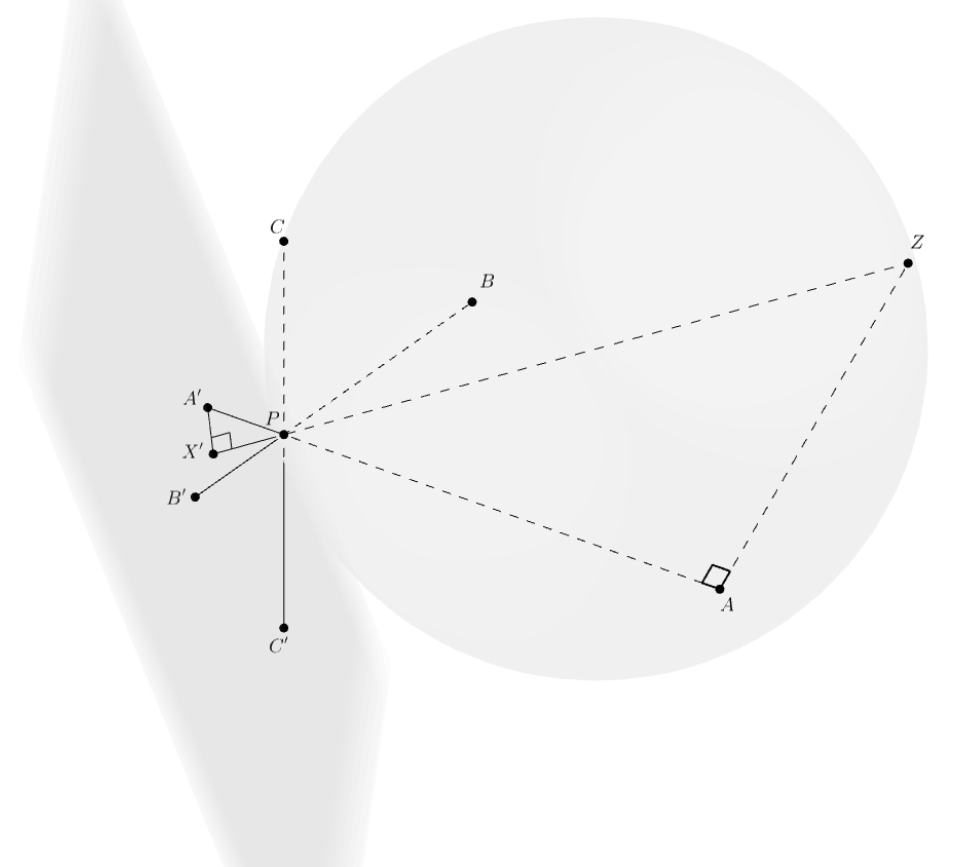
Далее, пусть
,
— середины хорд, или проекции
на
соответственно. В силу перпендикулярности
хорд:
значит, — середина
Окружности
являющиеся образом прямых
при нашем преобразовании, проходят через
фиксированную точку, а именно через точку
на продолжении отрезка
за точку
такую, что
Значит, и
прямые
проходят через фиксированную точку.
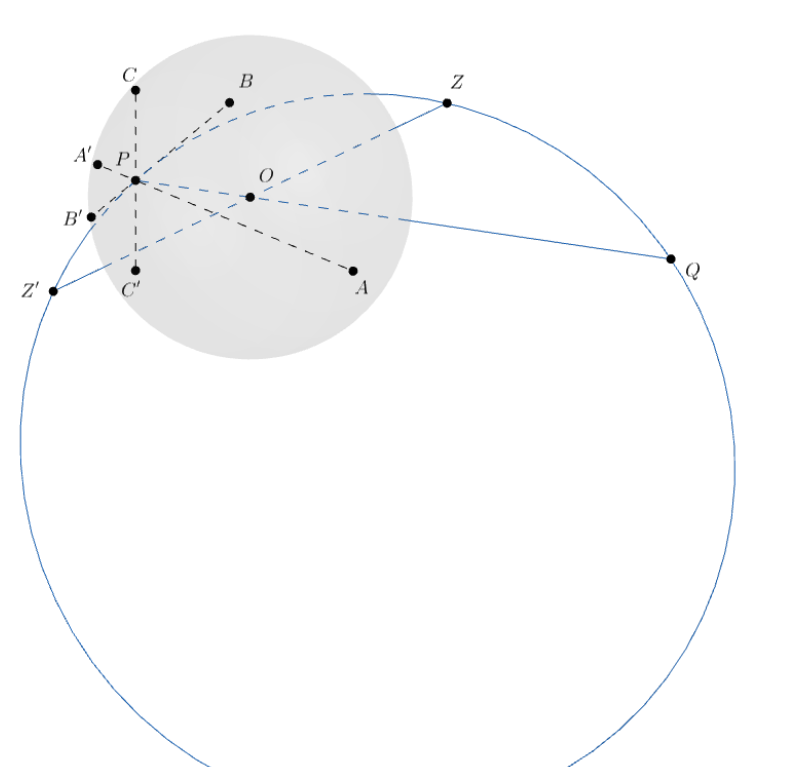
Ошибка.
Попробуйте повторить позже
В окружность вписан остроугольный треугольник
в котором
Пусть
и
– середины меньшей и большей дуги
окружности
соответственно. Пусть
– основание перпендикуляра, опущенного из точки
на отрезок
Докажите, что
окружность, описанная около треугольника
делит отрезок
пополам.
Источники:
Подсказка 1
Как с помощью инверсии можно показать, что некоторая окружность проходит через вершину треугольника?
Подсказка 2
Часто в этом помогает рассмотрения композиции инверсии с центром в данной вершине и симметрии относительно биссектрисы внутреннего угла данной вершины, которая меняет вершины треугольника местами. Во что перейдут точки из условии при рассмотрении такого преобразования?
Подсказка 3
Точка M перейдет в M' на BC такую, что угол BQ'M' = 90°, где Q' — основания биссектрисы внешнего угла, точка S — середина BP — в точку S' — отражение вершины B относительно основания биссектрисы из нее. Таким образом, достаточно показать, что точки A, S', M' лежат на одной прямой. Как это сделать?
Подсказка 4
Достаточно показать, что AP' / AQ' = P'S' / Q'M'. Воспользуйтесь свойством оснований биссектрис P'A / AQ' = P'C / CQ' и подобием треугольников P'BC и Q'M'C.
Рассмотрим композицию инверсии с центром в вершине и инверсии с радиусом
. При этой инверсии точки
и
меняются
местами, а окружность
переходит в прямую
Точка
перейдет в точку
пересечения прямой
и
— основание биссектрисы внешнего угла
. Точка
в перейдет точку на
такую, что
,
перейдет в точку
пересечения прямой
и
— основание биссектрисы угла
, то есть точка
— середина
отрезка
перейдет в отражение
точки
относительно
. Таким образом, достаточно показать, что точки
лежат на одной прямой, поскольку тогда после обратного преобразования точки
лежат на одной
окружности.
![]()
Осталось заметить, что в силу параллельности прямых И
треугольнкии
и
подобны, следовательно,
что в силу свойств основания биссектрисы внешнего угла равно Таким образом,
то есть треугольники и
подобны, значит точки
лежат на одной прямой.
![]()
Ошибка.
Попробуйте повторить позже
В треугольнике проведена биссектриса
Точки
и
являются проекциями вершин
и
на
Окружность с
диаметром
пересекает
в точках
и
Докажите, что
![]()
Пусть – точки, симметричные
относительно биссектрисы
Сами точки
– середины оснований
получившейся равнобокой трапеции
Пусть
– точка пересечения ее диагоналей. Мы уже знаем, что
инверсна
относительно окружности с диаметром
В точке
также пересекаются диагонали равнобокой трапеции
вписанной в эту
окружность. Мы также знаем, что
инверсна точке пересечения продолжений боковых сторон
и
относительно окружности с
диаметром
Получается, что
– точка пересечения
и
Из симметричности картинки теперь следует утверждение
задачи.
Ошибка.
Попробуйте повторить позже
Боковые стороны и
трапеции
являются соответственно хордами окружностей
и
касающихся друг друга
внешним образом. Градусные меры касающихся дуг
и
равны
и
Окружности
и
также имеют хорды
и
соответственно. Их дуги
и
расположенные с той же стороны от хорд, что соответствующие дуги первых двух окружностей,
имеют градусные меры
и
Докажите, что
и
тоже касаются.
Источники:
Подсказка 1
Давайте проведем конструктивное доказательство и явно покажем, как задаются окружности ω₃ и ω₄. Проще всего это сделать, если явно указать преобразование, сохраняющее касание, которое перевело бы ω₁ в ω₃, ω₂ в ω₄. Что может являться данным преобразованием?
Подсказка 2
Когда дело доходит до сохранения касания при преобразовании, в первую очередь стоит думать об инверсии и аффинных преобразованиях. Если мы хотим перевести ω₁ в ω₃, то было бы проще перевести точку A в C, B в D. Для этого чаще всего используется композиции инверсии в центре точке O — пересечения точек AB и CD - и симметрии относительно биссектрисы угла AOC. Какой коэффициент должен быть у данной инверсии?
Подсказка 3
Коэффициент √(OA ⋅OC) = √(OB ⋅OD). Обоснуйте, что образы окружностей ω₁ и ω₂ являются окружностями ω₃ и ω₄.
Пусть — точка пересечения прямых
и
— точка касания окружностей
и
Рассмотрим композицию инверсии с
центром в точке
радиусом
и симметрии относительно внутренней биссектрисы угла
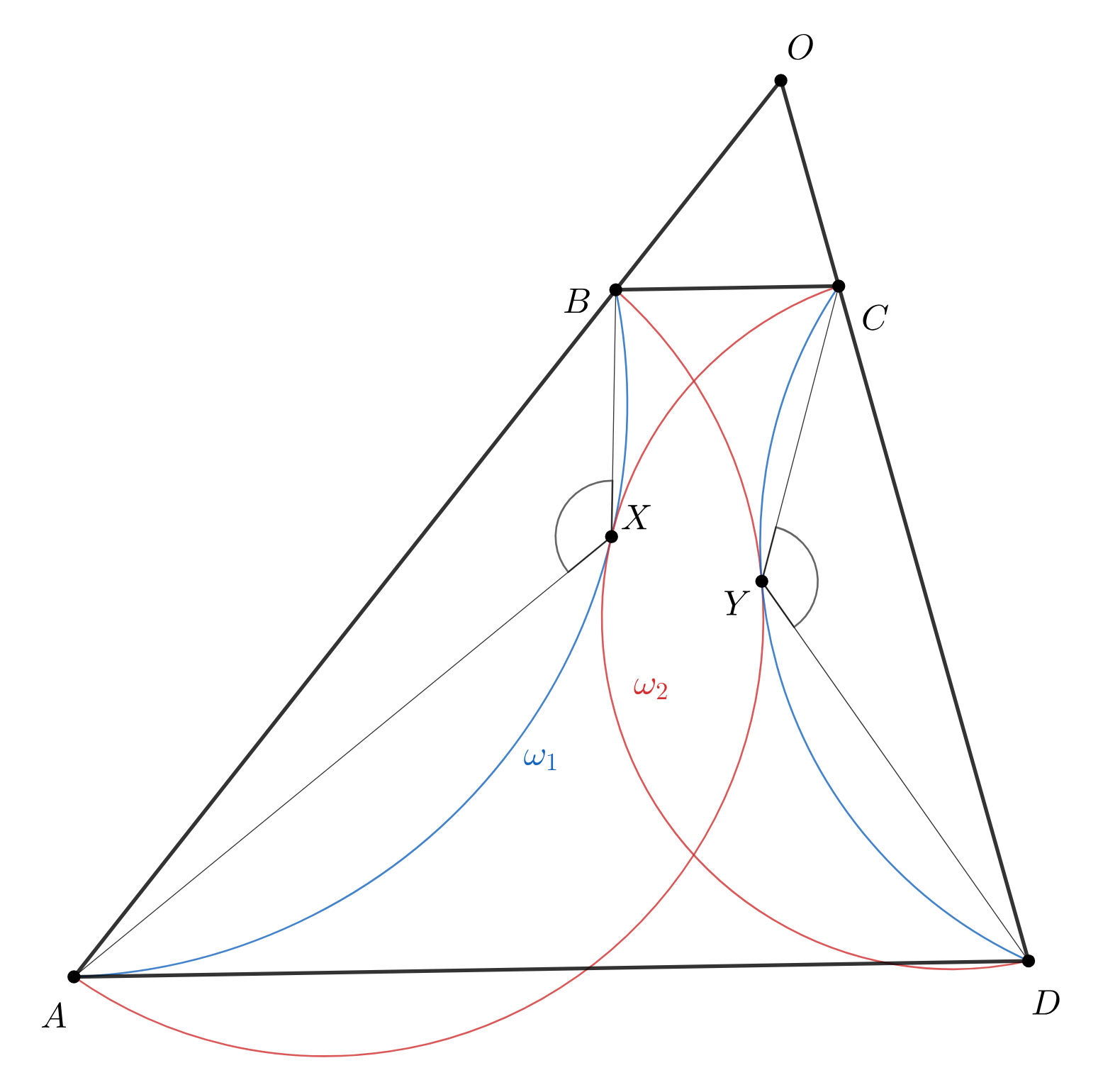
Данное преобразование меняет пары точек и
и
Пусть
— образ точки
тогда окружности
и
касаются, т.к. являются образом окружностей
и
Осталось заметить, что следовательно,
совпадает с
аналогично,
совпадает с
Ошибка.
Попробуйте повторить позже
В треугольнике проведена биссектриса
(точка
лежит на отрезке
). Прямая
пересекает окружность
описанную около треугольника
в точках
и
Окружность
построенная на отрезке
как на диаметре, пересекает
окружность
в точках
и
Докажите, что прямая, симметричная прямой
относительно прямой
содержит медиану
треугольника
Источники:
Подсказка 1
Так, нужно подумать… То есть у нас есть биссектриса и середина стороны в задаче, а также есть описанная окружность. На какой факт нам это намекает?
Подсказка 2
Верно, на тот факт, что биссектриса и серпер пересекаются на описанной окружности треугольника. Тогда пусть они пересеклись в точке Е. Что интересного можно заметить если продлить отрезок EM до пересечения с описанной окружностью(пусть точка пересечения - точка Х)?
Подсказка 3
Конечно, можно заметить, что F,D,X - лежат на 1 прямой. Почему это так? Ну понятно почему, XFE - прямой, так как опирается на диаметр окружности (ABC), и DFE - прямой, так как опирается на диаметр окружности, построенной на DE как на диаметре. Хмм… А что теперь нам это дает? Какие равные углы теперь можно отметить?
Подсказка 4
Действительно, мы можем заметить равенство углов FBE и FXE, в силу того, что они опираются на одну хорду FE. Значит, нам надо доказать, что углы FXE и MBE равны! А как это можно удобно переформулировать?
Подсказка 5
Это можно переформулировать как доказательство вписанности BDMX. Осталось понять почему сумма углов EBX и XMA равна 180 градусов, и задача будет решена!
Первое решение. Пусть — медиана треугольника. Так как биссектриса
и серединный перпендикуляр к
проходят через
одну и ту же точку (середину дуги
), то
Пусть
пересекается с окружностью в точке
Из сказанного выше следует,
что
— диаметр окружности
.png)
Надо доказать, что и
симметричны относительно биссектрисы, то есть
При этом как опирающиеся на одну дугу вписанные углы.
По условию прямой, а ещё опирающийся на диаметр вписанный угол
тоже прямой. Поэтому точки
коллинеарны. Тогда
Остаётся доказать равенство
Это равенство следует из того, четырёхугольник можно вписать в окружность. Действительно,
при этом
______________________________________________________________________________________________________________________________________________________
Второе решение.
![]()
Сделаем симметрию относительно биссектрисы угла и инверсию с таким радиусом, чтобы
и
где звездочкой
обозначаем образ точки под действием композиции преобразований. Заметим что
и
так как прямая
переходит в
дугу
и наоборот, а прямая
переходит сама в себя. Окружность, построенная на
тем самым переходит в окружность,
центр которой все лежит на
а точки ее пересечения с
это
и
То есть, эта окружность переходит в себя. Точка
переходит в точку
вторую точку пересечения окружности и прямой
Известно, что
– середина дуги
а
так
как
– диаметр окружности. Получаем, что
высота в равнобедренном треугольника
значит
– середина
Получается, что
содержит медиану треугольника
причем
симметрична
относительно биссектрисы угла


