Закл до 2015
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Трапеция с основаниями
и
вписана в окружность
Окружность
проходит через точки
и
пересекает отрезки
в точках
соответственно. Точки
и
симметричны точкам
и
относительно середин отрезков
и
соответственно. Докажите, что точки
и
лежат на одной
окружности.
Подсказка 1
Используем для доказательства степень точки. Чтобы доказать вписанность четырёхугольника, нужно показать равенство произведений отрезков секущих, например, из C.
Подсказка 2
Из условия следует, что CB₂ = BB₁ и CA₂ = AA₁. Тогда получается, нам нужно проверить равенства произведений, которые являются степенями точек уже относительно окружности ω.
Четырехугольник вписан в окружность только тогда, когда произведение длин отрезков секущиx
и
равны.
Точки и
симметричны точкам
и
относительно середин отрезков
и
соответственно, следовательно,
и
то есть достаточно проверить равенство
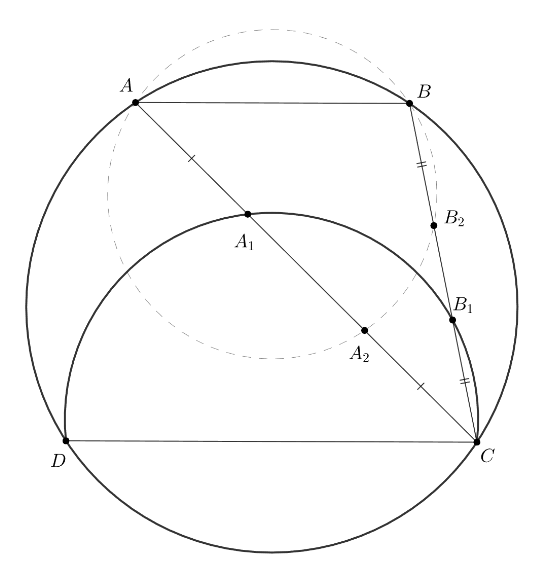
Левая и правая часть равны степеням точек и
относительно окружности
соответственно, и равны, поскольку
точки
симметричны относительно серединного перпендикуляра к отрезку
а значит, равноудалены от центра
Ошибка.
Попробуйте повторить позже
На доске написали попарно различных натуральных чисел
Затем под каждым числом
написали число
полученное прибавлением к
наибольшего общего делителя остальных
исходных чисел. Какое наименьшее количество попарно
различных чисел может быть среди
Источники:
Подсказка 1:
Решение стоит начать с придумывания хорошего примера.
Подсказка 2:
Итак, вы придумали пример на 99 (если не придумали, придумайте). А как насчёт того, чтобы доказать, что всегда найдется 99 различных бэшек?
Подсказка 3:
Пусть dᵢ - НОД всех ашек, кроме i-й. Попробуйте рассмотреть наибольшее из них. Как с ним связаны ашки и бэшки?
Если положить и
при
то
так что среди чисел
будет не больше
различных.
Осталось доказать, что среди чисел
всегда найдутся
различных чисел.
Без ограничения общности можно считать, что Пусть
— наибольший общий делитель всех
исходных чисел,
кроме
тогда
Пусть
— наибольшее из чисел
Тогда при
числа
делятся на
Следовательно, при
и
разность
также делится на
Поскольку она положительна,
Поэтому
откуда Итак, мы установили, что
при
Стало быть, все
чисел
при
различны.
Ошибка.
Попробуйте повторить позже
Положительные числа таковы, что
и
Докажите, что какие-либо
два из чисел
отличаются больше, чем на
Источники:
Перемножив равенство
и неравенство
получим неравенство
Возведем теперь в квадрат равенство
Получим
Вычитая из неравенства равенство
получаем
или
Предположим теперь, что любые два числа отличаются не больше, чем на Тогда квадрат их разности не больше
и из
получаем неравенство
Но, если вычесть из квадрата равенства равенство
получится равенство
что противоречит Значит, найдутся два числа, отличающиеся больше, чем на
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник . Окружность, проходящая через вершину
и центр
его описанной окружности, вторично
пересекает стороны
и
в точках
и
соответственно. Докажите, что точка пересечения высот треугольника
лежит на
прямой
.
Источники:
Обозначим Тогда
Поскольку четырёхугольник
вписан,
и
Пусть
— высота треугольника
а
— точка пересечения прямых
и
Без ограничения
общности можно считать, точка
лежит на луче
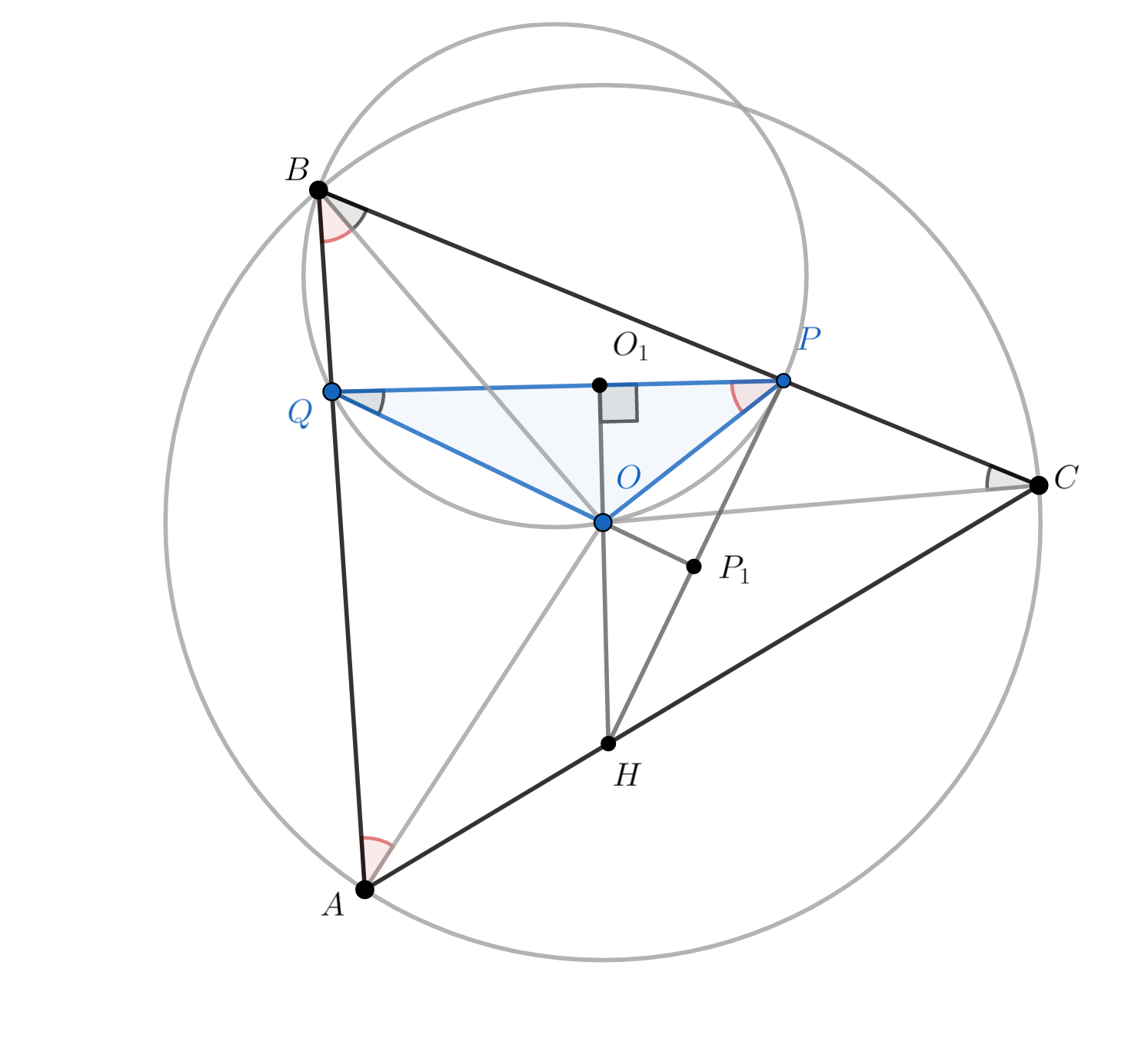
Угол — внешний угол треугольника
поэтому
Значит, четырёхугольник
вписан, и
Пусть
— точка пересечения прямых
и
Вновь по свойству внешних
углов
Итак, то есть
— ортоцентр треугольника
Ошибка.
Попробуйте повторить позже
Даны трое чашечных весов без гирь, из которых ровно одни сломаны: их показания произвольны, и мы не знаем, какие весы
неисправны. Докажите, что из монет можно определить одну фальшивую (более легкую) не более, чем за
взвешивание.
Источники:
Докажем индукцией по
База. Для удобства занумеруем монеты числами от до
и запишем их в троичной записи (таким образом, каждой монете
сопоставлена пара цифр от
до
). Первое взвешивание делаем первыми весами в соответствии с первой цифрой номера: на левую чашу
кладем монеты, у номера которых первая цифра
на правую — у которых она
Второе взвешивание делаем аналогично вторыми
весами в соответствии со второй цифрой номера. Знак
указывает на то, что фальшивая монета среди чисел с
на первом/втором
месте,
— что она среди чисел с
на первом/втором месте,
— что среди чисел с
на первом/втором месте. После проведения
взвешиваний можно перенумеровать числа так, чтобы результат первого взвешивания указывал на число с
на первом месте, а
второго — с
на втором. Тогда
монеты без нулей в номере точно не фальшивые (иначе соврали и первые, и вторые
весы).
Теперь разобьем монеты на три группы следующим образом: в одну поместим в другую
и
в третью —
и
дополним
все группы до трех монет точно не фальшивыми и взвесим третьими весами. Если весы сказали, что фальшивая в группе с
то это и есть
(иначе двое весов соврали), и четвертое взвешивание не понадобилось. Если взвешивание сказало, что фальшивая в группе с
и
то третьи весы противоречат вторым. Поэтому хотя бы одни из них соврали, а значит, первые точно исправны. Но тогда у фальшивой
первая цифра действительно
таким образом, остались лишь три кандидата на фальшивую монету и одни точно исправные весы,
которыми мы находим фальшивую монету за
ход. Аналогично поступаем, если третье взвешивание сказало, что фальшивая монета в
группе с
и
Переход. Разобьём монет на одну
куч по
в каждой. Будем считать каждую кучу за одну монету (куча с фальшивой
монетой легче). Тогда по рассуждениям из базы мы либо находим за
взвешивания кучу с фальшивой монетой и далее работаем с ней,
пользуясь предположением, либо за
взвешивания мы находим рабочие весы и три кучи, среди которых есть куча с фальшивой
монетой. Во втором случае, нам хватит
взвешиваний, если постоянно делить кучу на три кучи с одинаковым числом
монет.
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике точки
и
— точки пересечения высот и медиан соответственно. Через вершины
и
проведены прямые, перпендикулярные прямым
соответственно. Докажите, что точка пересечения медиан треугольника,
образованного проведёнными прямыми, лежит на прямой
Источники:
Пусть — треугольник, образованный проведёнными прямыми и
— точка пересечения его медиан. Мы докажем, что
является серединой отрезка
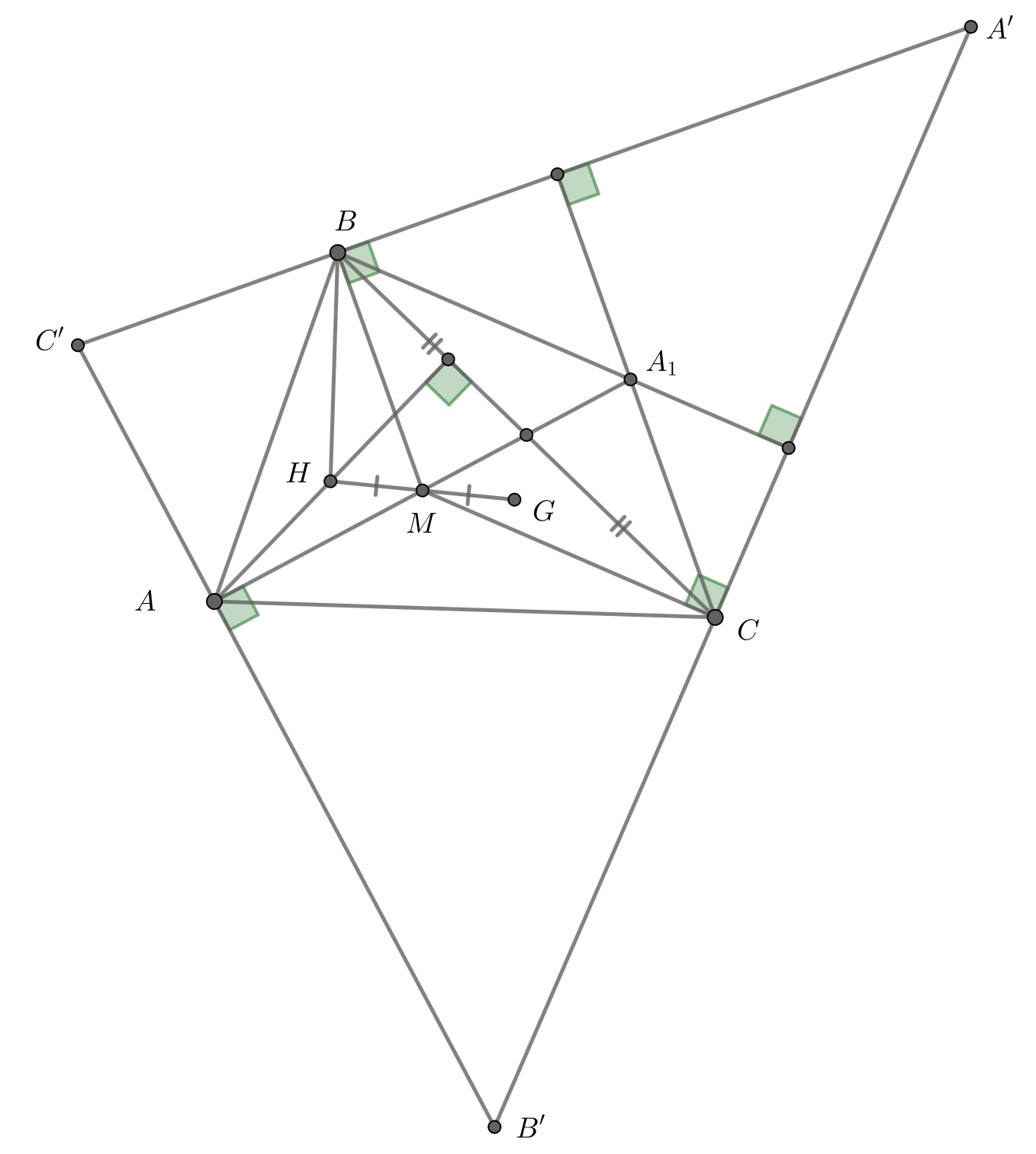
Достроим треугольник до параллелограмма
Отрезок
делит сторону
пополам, поэтому
лежит на
прямой
причём
Кроме того,
и
поэтому
и
— высоты треугольника
Значит,
— ортоцентр этого треугольника и
Стороны треугольника перпендикулярны сторонам треугольника
соответственно, поэтому эти треугольники подобны,
причём соответствующие прямые
и
содержащие медианы этих треугольников, перпендикулярны. Значит, прямая
совпадает с прямой
Пусть
— точка, симметричная точке
относительно
Треугольники
и
симметричны
относительно
поэтому
Отсюда следует, что
лежит на прямой
Аналогично
лежит на прямой
то
есть
совпадает с
Ошибка.
Попробуйте повторить позже
Два игрока по очереди проводят диагонали в правильном -угольнике
Разрешается проводить диагональ, если она
пересекается (по внутренним точкам) с четным числом ранее проведенных диагоналей (и не была проведена раньше). Проигрывает игрок,
который не может сделать очередной ход. Қто выигрывает при правильной игре?
Источники:
Заметим, что по одну сторону от каждой диагонали находится чётное число вершин, а по другую — нечётное. Поэтому каждую диагональ
пересекает чётное число других диагоналей угольника. Пусть в некоторый момент игры невозможно сделать ход,
тогда каждая непроведённая диагональ пересекает нечётное число уже проведённых, а следовательно, и нечётное число
непроведённых диагоналей. Такая ситуация возможна только тогда, когда непроведённых диагоналей чётное число(по лемме о
рукопожатиях).
Таким образом, если общее количество диагоналей в многоугольнике нечётно, то выиграет первый, а если чётно — второй.
В угольнике число диагоналей равно
то есть нечётно при чётном
и чётно при нечётном
При нечётном выигрывает второй, при чётном — первый
Ошибка.
Попробуйте повторить позже
Приведённые квадратные трёхчлены и
таковы, что уравнения
и
не имеют вещественных корней.
Докажите, что хотя бы одно из уравнений
и
тоже не имеет вещественных корней.
Источники:
Поскольку трёхчлены приведённые, их графики — параболы с ветвями, направленными вверх. Они принимают все значения от
минимального до Обозначим корни
как
а корни
как
Если какой-то из них не имеет корней, то
утверждение задачи очевидно.
Из условия не имеет корней, следовательно:
Аналогично, из не имеет корней:
Не умаляя общности тогда
и
следовательно
не имеет корней.
Ошибка.
Попробуйте повторить позже
Дана доска Некоторые пары центров соседних по стороне клеток соединили отрезками так, что получилась замкнутая
несамопересекающаяся ломаная, симметричная относительно одной из диагоналей доски. Докажите, что длина ломаной не больше
Источники:
Ясно, что ломаная пересекает диагональ. Пусть — одна из вершин ломаной, лежащая на диагонали. Будем двигаться по ломаной, пока
не попадём в первый раз снова в вершину
лежащую на диагонали. Из симметрии, если двигаться по ломаной из
в другую сторону, то
также окажется первой вершиной на диагонали, в которую мы попадём. При этом ломаная уже замкнётся, поэтому через остальные
центров клеток на диагонали ломаная не проходит.
Раскрасим доску в шахматном порядке так, чтобы диагональ была чёрной. Заметим, что на нашей ломаной белые и чёрные клетки
чередуются, поэтому их количества равны. Всего на доске чёрных клеток. Поскольку клетки диагонали чёрные и ломаная
не проходит через
из них, то она проходит не более чем через
чёрных клеток. Итого длина ломаной не более
Ошибка.
Попробуйте повторить позже
В стране городов. Между каждыми двумя из них проложена либо автомобильная, либо железная дорога. Турист хочет объехать страну,
побывав в каждом городе ровно один раз, и вернуться в город, с которого он начинал путешествие. Докажите, что турист может
выбрать город, с которого он начнет путешествие, и маршрут так, что ему придётся поменять вид транспорта не более одного
раза.
Источники:
Подсказка 1
Переформулируем задачу на языке графов. Нам дан полный граф с вершинами, рёбра которого покрашены в два цвета. Требуется доказать, что мы можем выделить в этом графе цикл, проходящий через все вершины, состоящий не более чем из двух одноцветных частей.
Подсказка 2
Понятно, что делать переход нужно от n+1 до n. Как «внедрить» в путь новую вершину после её удаления?
Подсказка 3
Внедрить её в путь в случае одноцветного пути несложно. А что делать с участком пути другого цвета?
Переформулируем задачу на языке графов. Нам дан полный граф с вершинами, рёбра которого покрашены в два цвета. Требуется
доказать, что мы можем выделить в этом графе цикл, проходящий через все вершины, состоящий не более чем из двух одноцветных частей.
Доказательство проведём по индукции.
База. Для полного графа с тремя вершинами утверждение очевидно.
Шаг индукции. Рассмотрим полный граф с вершиной. Удалим из рассмотрения одну вершину
с выходящими из неё ребрами.
Для оставшегося графа с
вершинами по предположению индукции существует цикл, проходящий через все вершины, состоящий не более
чем из двух одноцветных частей. Возможны два случая.
Все рёбра цикла окрашены в один цвет. Занумеруем вершины цикла по порядку
Тогда, удалив ребро
и соединив вершину
с вершинами
и
мы получим цикл, состоящий не более чем из двух одноцветных
частей.
2) Не все рёбра цикла окрашены в один цвет. Пусть в цикле есть две одноцветные части: (красная) и
(синяя). Посмотрим на цвет ребра
Если это ребро красное, то цикл
— искомый, если же оно синее, то
искомым будет цикл
Ошибка.
Попробуйте повторить позже
В кабинете президента стоят телефона, любые два из которых соединены проводом одного из четырех цветов. Известно, что провода
всех четырех цветов присутствуют. Всегда ли можно выбрать несколько телефонов так, чтобы среди соединяющих их проводов встречались
провода ровно трех цветов?
Источники:
Построим граф, вершины которого соответствуют телефонам, а рёбра – проводам. Рассмотрим наименьший такой набор вершин данного графа, что среди соединяющих эти вершины рёбер присутствуют рёбра всех четырёх цветов. Удалим из этого набора произвольную вершину. Поскольку набор был наименьший, среди рёбер, соединяющих оставшиеся вершины, присутствуют уже не все цвета.
Если среди этих рёбер присутствуют рёбра ровно трёх цветов, то искомый набор найден.
В противном случае среди рёбер, выходящих из удалённой вершины в другие вершины нашего набора, присутствуют как минимум два цвета, которые исчезнут после удаления этой вершины.
Рассмотрим два ребра этих цветов, выходящие из удалённой вершины в другие вершины набора. Тогда ребро, соединяющее их концы, должно иметь цвет, отличный от цветов этих двух рёбер. Таким образом, в графе нашёлся треугольник, все рёбра которого имеют попарно различные цвета.
Это означает, что требуемый набор вершин можно выбрать всегда.
Да, можно
Ошибка.
Попробуйте повторить позже
В ячейки куба поставлены по одному числа
Из одного углового кубика в противоположный угловой
отправляются два червяка. Каждый из них может проползать в соседний по грани кубик, при этом первый может проползать, если число в
соседнем кубике отличается на
второй — если отличается на
Существует ли такая расстановка чисел, что оба червяка смогут
добраться до противоположного углового кубика?
Подсказка 1
Для начала поймите, сколько ходов точно потребуется червякам, чтоб дойти до конечной клетки.
Подсказка 2
Чтоб дойти до конечной клетки надо сделать хотя бы 30 ходов. Пусть в начальной клетке стоит число a, а в конечной b. Можно считать, что a < b. Клетки с какими номерами тогда точно должны пройти эти червячки?
Подсказка 3
Правильно! Первый червячок должен идти по клеткам с номерами a + 8k, а второй по клеткам с номерами a + 9k. Теперь стоит подумать, есть ли у путей первого и второго червяки общие клетки.
Подсказка 4
На самом деле есть. Например клетка с номером a + 72. Если покрасить в шахматную раскраску клетки, то какого цвета будет клетка для каждого из червяков (если начальная клетка черная)?
Предположим, что существует такая расстановка чисел, что оба червяка доберутся до противоположного углового кубика. Пусть числа,
стоящие в начальном и конечном угловых кубиках равны и
соответственно. Можно считать, что
Заметим, что числа
и
отличаются по крайней мере на
так как второй червяк сделал хотя бы
ходов (как минимум по
в
каждом из трех направлений). Также можно считать, что каждый червяк не заползает в каждый кубик больше одного
раза (иначе путь от этого кубика до него же можно опустить). Тогда первый червяк должен последовательно проползти
через кубики с числами
Второй должен последовательно проползти через кубики с
числами
Рассмотрим теперь шахматную раскраску нашего куба. Можно считать, что
кубик с числом
покрашен в черный цвет. Заметим, что соседние по грани кубики должны иметь разные цвета. Это
означает, что кубики с числами
должны быть покрашены в черный цвет (следует из пути
-ого
червы), а кубики
должны быть покрашены в белый цвет (следует из пути
-ого червя). То
есть кубик с числом
должен быть покрашен и в черный, и в белый цвета. Полученное противоречие завершает
доказательство.
Не существует
Ошибка.
Попробуйте повторить позже
В компании из человека для любых
человек найдётся отличный от них человек, знакомый с каждым из них. Докажите, что в
этой компании есть человек, знающий всех.
Источники:
Очевидно, что есть двое знакомых, и если есть попарно знакомых (где
), то по условию найдётся отличный от них человек,
знакомый со всеми этими
людьми. Отсюда следует, что найдутся
попарно знакомых:
Рассмотрим
остальных
человек. По условию существует отличный от них человек
знающий их всех. Но тогда
знаком со
всеми.
Ошибка.
Попробуйте повторить позже
Попарно различные числа
и
таковы, что уравнения
и
имеют общий действительный
корень. Кроме того, общий действительный корень имеют уравнения
и
Найдите сумму
Источники:
Подсказка 1
Уравнения имеют общий корень, попробуйте использовать это условие, подставив общий корень в каждое из уравнений. Можно ли выйти на второй корень с помощью первого?
Подсказка 2
Да, общий корень первых двух уравнений равен: (c-1)/(a-b). Чему равен второй корень первого уравнения?(посмотрите на его свободный член)
Подсказка 3
Верно, он равен (a-b)/(c-1). Тогда попробуйте подставить общий корень из второго условия! Что интересное мы обнаружим?
Подсказка 4
Да, мы обнаружим, что второй общий корень равен (a-b)/(c-1). То есть, у уравнения из первой пары и у уравнения из второй пары тоже есть общий корень! Давайте снова подставим его и найдем значение! И мы сможем найти сумму всех коэффициентов!
Пусть у первых двух уравнений общий корень . Тогда
и
(по условию
).
Тогда второй корень у уравнения
по теореме Виета это
. Отсюда
. Посмотрим на оставшиеся
уравнения.
Пусть у последних двух уравнений общий корень . Тогда
и
. Значит
корень
и
. Отсюда
. Если
, то у уравнения
нет корней ?! Значит
. Подставим 1 во все уравнения, где
корень и получим
и
. Значит
.
Ошибка.
Попробуйте повторить позже
В микросхеме контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по
очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя – либо один, либо три провода.
Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной
игре?
Источники:
Разделим контакты на группы
по
контактов. Контакт в каждой группе пронумеруем номером от
до
и
будем обозначать
— контакты в соответствующих группах с номером
Если Вася перерезает контакт в
одной группе, например,
то Петя режет
Если Вася режет провод между контактами из
разных групп с одинаковыми номерами, например,
то Петя перережет провод
Если Вася режет провод
между контактами из разных групп, например,
причем
то Петя режет
и
Из описанной
стратегии Пети следует, что провода, которые ему нужно перерезать, не будут отрезаны до его хода, поэтому ход Пети всегда
возможен.
Таким образом, Петя всякий раз поддерживает на свой ход инвариант: у контактов отходит одинаковое число проводов,
при этом от одного из них столько же проводов отходило уже после хода Васи. Поэтому отрезание последнего провода от одного из
контактов случится после хода Васи и, следовательно, Петя выиграет.
Петя
Ошибка.
Попробуйте повторить позже
В Думе депутатов, которые образовали
комитетов по
человек в каждом. Докажите, что найдутся два комитета, имеющие
не менее четырёх общих членов.
Источники:
Предположим обратное: для любых двух комитетов имеется не более общих членов. Тогда воспользуемся леммой Корради.
—
множество депутатов,
— количество комитетов (подмножества
),
— количество человек в комитете (количество
элементов в подмножестве),
— комитет №
Тогда из предположения следует, что
при
По лемме получаем оценку
на мощность множества депутатов:
Получаем противоречие. Значит, нашлись комитета, имеющих более
общих членов.
Ошибка.
Попробуйте повторить позже
Можно ли на прямоугольник положить по линиям сетки несколько уголков из
клеток (возможно, с перекрытиями) так, чтобы
каждая клетка была покрыта одинаковым числом уголков?
Назовём покрытием ситуацию, когда уголок покрыл какую-то клетку. Получается, что каждый уголок делает три покрытия. Рассмотрим
клетки с координатами (координаты целые и начинаются с
Их
По условию у каждой клетки должно быть одинаковое
количество покрытий. Это значит, что суммарно эти
клеток имеют
от всех покрытий. С другой стороны, каждый уголок может
покрывать не более одной отмеченной клетки. Это означает, что суммарное количество покрытий этих
клеток не превосходит
от
общего числа покрытий. Таким образом, нельзя.
Нет
Ошибка.
Попробуйте повторить позже
Известно, что и
— квадратные трехчлены. Может ли уравнение
иметь корни
,
,
,
,
,
,
и
?
Источники:
Подсказка 1
Предположим противное и попробуем найти противоречие. Данные корни находятся достаточно "близко", а что мы можем наказать о корнях f(x)? Что интересного можно найти у параболы?
Подсказка 2
У параболы есть ось симметрии! Корнями f являются различные значения функции g, но их больше двух - что мы тогда можем сказать про них?
Подсказка 3
Какие-то из значений функции g в точках, равных h(x), где 1≤x≤8, совпадают! Попробуем упорядочить такие точки, найдя ось симметрии f(g(h(x))).
Подсказка 4
Т.к. ось симметрии f(g(h(x))) есть x = 4.5, то мы точно можем упорядочить h(1), h(2), h(3), h(4) и провести рассуждения выше только для этих точек (их уже больше двух, что хорошо)
Предположим, что да. Пусть ось симметрии —
тогда понятно, что она же является осью симметрии многочлена
Нам известно, что в точках
многочлен зануляется, значит, его осью симметрии является прямая
Таким
образом,
.
Заметим, что многочлен имеет корни
и
Однако у него не более двух корней, значит, какие-то
совпадают.
В силу и наличия оси симметрии у многочлена
получаем, что
Из
этого следует, что
Однако если расписать это равенство для трёхчлена
то мы получим, что
то есть придём к противоречию.
Ошибка.
Попробуйте повторить позже
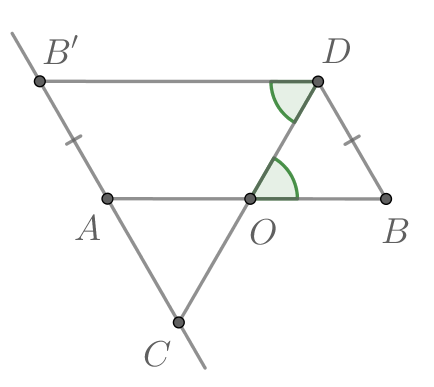
Отрезки и
длины 1 пересекаются в точке
причём
Докажите, что
Источники:
Подсказка 1
Каким неравенством мы привыкли сравнивать отрезки?
Подсказка 2
Очень хочется воспользоваться неравенством треугольника. Но BD находится слишком "далеко" от AC( Давайте тогда попробуем мысленно "перенести" BD так, чтобы сохранить его длину. Как это можно сделать?
Подсказка 3
Проведите через точку A прямую, параллельную BD. Какую точку хочется на ней отметить?
Подсказка 4
Отметьте точку B' на построенной прямой так, чтобы B'A было равно BD. Какая фигура образовалась?
Подсказка 5
Как воспользоваться данным в условии углом? Быть может, из параллельности его можно куда-то перетащить? :)
Проведем через точку прямую, параллельную
Отметим на ней точку
так, чтобы
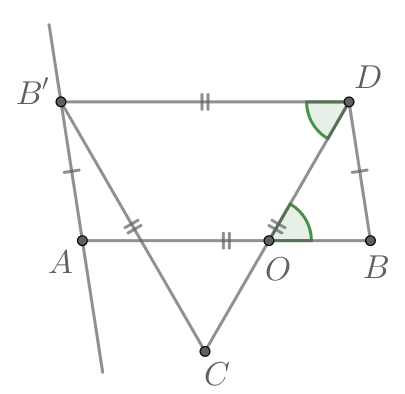
В четырехугольнике по постороению сторона
равна и параллельна стороне
следовательно,
— параллелограмм и
следовательно,
как накрест
лежащие.
Рассмотрим треугольник В нем угол между равными сторонами
и
равен
значит, это треугольник
равносторонний и
По неравенству треугольника для
получаем
причем
Тогда
что и требовалось доказать. Единственный случай, в котором неравенство обращается
в равенство, достигается, когда
попадает на прямую
Это равносильно тому, что
(т.к. отрезок
мы
строили как параллельный
).
Ошибка.
Попробуйте повторить позже
Целые числа таковы, что
Докажите, что тогда
делится на
Источники:
Подсказка 1
Предположим, что данное число не кратно 3. Что можно сказать про числа x-y, y-z, z-x?
Подсказка 2
Никакое из них не кратно 3, то есть числа x, y, z дают различные остатки по модулю 3. Как можно получить противоречие исходя из этого?
Подсказка 3
В этом случае число x+y+z сравнимо с числом 1+2+3 по модулю 3, то есть кратно ему, что невозможно. Так, мы поняли, что среди чисел x, y, z найдутся хотя бы два с одинаковым остатком при делении 3. Как это можно использовать, чтобы доказать делимость на 27?
Докажем, что числа и
дают одинаковые остатки при делении на
Тогда из условия будет следовать, что число
делится на
Если числа и
дают различные остатки при делении на три, то число
не делится на
а число
наоборот, делится на
Следовательно, по крайней мере, два из трех чисел
дают одинаковые остатки при делении на
Но тогда
число
делится на
а для этого необходимо, чтобы и третье число давало тот же остаток при делении на
что и первые два числа.



