Тема Закл (финал) 11 класс

Закл до 2015

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 11 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#75649Максимум баллов за задание: 7

Исходно на доске написаны многочлены $x2− 4x$ и $x3− 3x2+ 5.$ Если на доске написаны многочлены $f(x)$ и $g(x),$ разрешается дописать на неё многочлены $f(x)+ g(x),f(x)g(x),f(g(x))$ и $cf(x),$ где $c$ — произвольная (не обязательно целая) константа. Может ли на доске после нескольких операций появиться многочлен вида $n x − 1$ (при натуральном $n$ )?

Источники: Всеросс., 2014, ЗЭ, 11.7(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка

Понять, какие многочлены получатся очень тяжело, но легче посмотреть на их производные. Поймите, что будет общего у всех производных полученных функций.

Показать ответ и решение

Рассмотрим производные изначальных многочленов: $(x2− 4x)′ = 2x − 4,(x3 − 3x2+ 5)′ = 3x2− 6x.$ Обе производные имеют нули в $x =2.$

Теперь докажем следующую лемму:

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Имеется множество функций, каждая из которых имеет ноль производной в заданной точке. Тогда, любая новая функция, полученная способом, описанным в задаче, из функций множества, тоже будет иметь корень производной в этой точке.

Доказательство леммы. Пусть новая функция $h$ была получена из функций $f$ и $g$ по одному из способов, упомянутых в условии. По условию леммы имеется такое фиксированное $x =a,$ что $′ ′ f (a)= g(a)= 0.$

1) $h =f +g ⇒ h′ =f′+ g′ ⇒ h′(a)= f′(a)+ g′(a)= 0.$ Значит, $x= a$ — ноль функции $h.$

2) $h =f ⋅g ⇒ h′ = f′⋅g+ f ⋅g′ ⇒ h′(a)= f′(a)⋅g(a)+g′(a)⋅f(a)=0.$ Значит, $x =a$ — ноль функции $h.$

3) $h(x)= f(g(x)) ⇒ h′ = f′(g(x))⋅g′(x) ⇒ h′(a)= f′(g(a))⋅g′(a)= 0.$ Значит, $x =a$ — ноль функции $h.$

4) $h =c ⋅f ⇒ h′ =c ⋅f′ ⇒ h′(a)= c⋅f′(a)= 0.$ Значит, $x= a$ — ноль функции $h.$

______________________________________________________________________________________________________________________________________________________

Лемма доказана. Вернемся к исходной задаче. По лемме мы получаем, что каждая новая функция на доске будет иметь ноль производной в точке $x= 2.$ Но рассмотрим функцию, которую мы хотим получить: $(xn− 1)′ = nxn− 1.$ Заметим, что у ее производной не имеется нуля в точке $x= 2.$ Значит, по лемме мы не можем получить такую функцию.

Ответ:

Нет, не может

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#107061Максимум баллов за задание: 7

Сфера $ω$ проходит через вершину $S$ пирамиды $SABC$ и пересекает рёбра $SA,$ $SB$ и $SC$ вторично в точках $A , 1$ $B 1$ и $C 1$ соответственно. Сфера $Ω,$ описанная около пирамиды $SABC,$ пересекается с $ω$ по окружности, лежащей в плоскости, параллельной плоскости $(ABC ).$ Точки $A2,$ $B2$ и $C2$ симметричны точкам $A1,$ $B1$ и $C1$ относительно середин рёбер $SA,$ $SB$ и $SC$ соответственно. Докажите, что точки $A,$ $B,$ $C,$ $A2,$ $B2$ и $C2$ лежат на одной сфере.

Источники: Всеросс., 2014, ЗЭ, 11.6(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Принадлежность одной сфере можно показывать с помощью степеней точки, в этом случае необходимо показать равенство SA₂ * SA = SB₂ * SB = SC₂ * SC. Как его можно преобразовать из условия задачи? Что с ним делать дальше?

Подсказка 2

Рассмотрите поворот относительно прямой, проходящей через центры сфер, переводящий A в B (поймите, что такой существует). Что можно понять из этого поворота? Рассмотрите для этого образы точек S и A₁(с остальными аналогично).

Показать доказательство

Первое решение. Утверждение задачи эквивалентно равенству

SA2 ⋅SA= SB2 ⋅SB = SC2⋅SC

Значит, ввиду равенств $AA1 = SA2$ и двух аналогичных, достаточно доказать, что

AA ⋅AS = BB ⋅BS = CC ⋅CS 1 1 1

Пусть $ℓ$ — прямая, проходящая через центры сфер $Ω$ и $ω.$ Окружность пересечения этих сфер лежит в плоскости, перпендикулярной $ℓ,$ так что $ℓ⊥ (ABC).$ Это значит, что при повороте вокруг $ℓ$ описанная окружность треугольника $ABC$ переходит в себя, и подходящим таким поворотом можно точку $A$ перевести в $B.$ Пусть точки $S$ и $A1$ при этом повороте переходят в $S′$ и $A ′1$ (они тоже лежат на $ω,$ см. рис. слева). Тогда

AA1⋅AS = BA′⋅BS ′ =BB1 ⋅BS 1

Равенство $AA1⋅AS =CC1 ⋅CS$ доказывается аналогично.

$PIC$

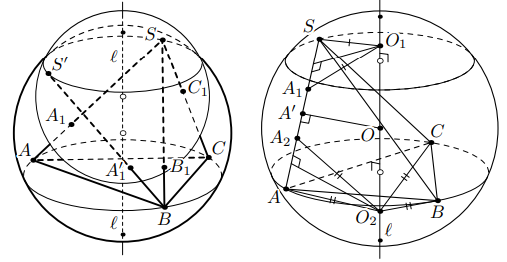
Второе решение. Обозначим через $O1$ и $O$ центры сфер $ω$ и $Ω$ соответственно. Как и в первом решении, введём прямую $ℓ,$ проходящую через $O$ и $O1;$ тогда $ℓ⊥ (ABC ).$

Пусть $O2$ — точка, симметричная $O1$ относительно $O.$ Тогда $O2$ лежит на $ℓ,$ откуда $O2A =O2B = O2C;$ обозначим $r =O2A.$ Далее, проекции точек $O2$ и $O1$ на $SA$ симметричны относительно проекции точки $O,$ т. е. относительно середины $A′$ отрезка $SA.$ Так как проекция точки $O1$ является серединой отрезка $SA1,$ из симметрии относительно $A′$ получаем, что проекция точки $O2$ — это середина отрезка $AA2.$ Значит, $A2O2 = AO2 =r.$ Аналогично показывается, что $B2O2 = C2O2 = r.$ Значит, требуемые шесть точек лежат на сфере с центром $O2$ и радиусом $r.$

Ошибка.
Попробуйте повторить позже

Задача 3#74058Максимум баллов за задание: 7

Глава Монетного двора хочет выпустить монеты $12$ номиналов (каждый — в натуральное число рублей) так, чтобы любую сумму от $1$ до $6543$ рублей можно было заплатить без сдачи, используя не более $8$ монет. Сможет ли он это сделать? (При уплате суммы можно использовать несколько монет одного номинала.)

Источники: Всеросс., 2013, ЗЭ, 11.7(см. olympiads.mccme.ru)

Показать ответ и решение

Заметим, что $94 =6561> 6543.$ Покажем, что можно выбрать $12$ номиналов так, чтобы с помощью не более чем $8$ монет можно было уплатить без сдачи любую сумму от $1$ до $6560$ рублей.

Покажем сначала, как выпустить монеты трёх номиналов, чтобы с помощью не более чем двух монет можно было уплатить без сдачи любую сумму от $1$ до $8$ рублей. Пусть номиналы равняются $1,3$ и $4$ рублям. Тогда $1= 1,2 =1 +1,3= 3,4 =4$ , $5 =4+ 1,6= 3+3,7= 4+ 3$ и $8 =4 +4.$

Пусть теперь Монетный двор изготовит монеты с номиналами $k k 9,3⋅9$ и $k 4⋅9$ рублей при $k= 0,1,2,3.$ Любое число $N$ от $1$ до $6560$ единственным образом представляется в виде $3 2 N =a3⋅9 + a2⋅9+ a1⋅9+ a0,$ где числа $ak$ могут принимать значения от $0$ до $8.$ (Фактически, это разложение числа $N$ в девятеричной системе счисления.) Как показано выше, сумма $k ak⋅9$ может быть получена не более чем двумя монетами. Таким образом, вся сумма $N$ может быть получена не более чем $4⋅2= 8$ монетами указанных номиналов, что и требовалось.

Ответ:

Да, сможет

Ошибка.
Попробуйте повторить позже

Задача 4#76703Максимум баллов за задание: 7

В окружность $Ω$ вписан остроугольный треугольник $ABC,$ в котором $AB >BC.$ Пусть $P$ и $Q$ – середины меньшей и большей дуги $AC$ окружности $Ω$ соответственно. Пусть $M$ – основание перпендикуляра, опущенного из точки $Q$ на отрезок $AB.$ Докажите, что окружность, описанная около треугольника $BMC,$ делит отрезок $BP$ пополам.

Источники: Всеросс., 2013, ЗЭ, 11.4(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Как с помощью инверсии можно показать, что некоторая окружность проходит через вершину треугольника?

Подсказка 2

Часто в этом помогает рассмотрения композиции инверсии с центром в данной вершине и симметрии относительно биссектрисы внутреннего угла данной вершины, которая меняет вершины треугольника местами. Во что перейдут точки из условии при рассмотрении такого преобразования?

Подсказка 3

Точка M перейдет в M' на BC такую, что угол BQ'M' = 90°, где Q' — основания биссектрисы внешнего угла, точка S — середина BP — в точку S' — отражение вершины B относительно основания биссектрисы из нее. Таким образом, достаточно показать, что точки A, S', M' лежат на одной прямой. Как это сделать?

Подсказка 4

Достаточно показать, что AP' / AQ' = P'S' / Q'M'. Воспользуйтесь свойством оснований биссектрис P'A / AQ' = P'C / CQ' и подобием треугольников P'BC и Q'M'C.

Показать доказательство

Рассмотрим композицию инверсии с центром в вершине $B$ и инверсии с радиусом $√BA-⋅BC-$ . При этой инверсии точки $A$ и $C$ меняются местами, а окружность $(BAC )$ переходит в прямую $AC.$ Точка $Q$ перейдет в точку $′ Q$ пересечения прямой $BQ$ и $AC$ — основание биссектрисы внешнего угла $B$ . Точка $M$ в перейдет точку на $BC$ такую, что $′ ′ ∘ BQ M =90$ , $P$ перейдет в точку $′ P$ пересечения прямой $BP$ и $AC$ — основание биссектрисы угла $B$ , то есть точка $S$ — середина отрезка $BP$ перейдет в отражение $′ S$ точки $B$ относительно $′ P$ . Таким образом, достаточно показать, что точки $′ A,S ,M$ лежат на одной прямой, поскольку тогда после обратного преобразования точки $B,C,M, S$ лежат на одной окружности.

$PIC$

Осталось заметить, что в силу параллельности прямых $BP ′$ И $Q′M′$ треугольнкии $BP ′C$ и $Q′M ′$ подобны, следовательно,

S′P′-= BP-′= P-′C-, M ′Q ′ M′Q′ C ′Q

что в силу свойств основания биссектрисы внешнего угла равно $P′A- P′Q.$ Таким образом,

S′P ′ P′A M-′Q′ = P′Q,

то есть треугольники $AP′S′$ и $AQ′M′$ подобны, значит точки $A′,S′,M ′$ лежат на одной прямой.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 5#127179Максимум баллов за задание: 7

Найдите все натуральные $k$ такие, что произведение первых $k$ нечетных простых чисел, уменьшенное на 1, является точной степенью натурального числа (большей, чем первая).

Источники: ВСОШ, ЗЭ, 2013, 11.3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть произведение нечётных простых чисел равно aⁿ + 1. Хотелось бы посмотреть на нечётные делители a. Но существуют ли они?

Подсказка 2

Если показатель степени не простой, можно ли его сделать простым?

Подсказка 3

Можно обратить внимание, что у нас есть нечётные простые из произведения, а также простое n. Давайте рассмотрим простой нечётный делитель числа a. Может их стоит сравнить между собой?

Подсказка 4

В произведении есть все простые вплоть до некого pₖ. Если n меньше pₖ, то оно входит в произведение простых. Что тогда можно сказать о aⁿ при рассмотрении по модулю n?

Подсказка 5

Тогда с одной стороны aⁿ + 1 делится на n, но по малой теореме Ферма и aⁿ − a тоже делится на n. Не противоречат ли эти две делимости друг другу?

Показать ответ и решение

Пусть $n ≥2,$ и $3= p < ⋅⋅⋅< p 1 k$ — первые $k$ нечётных простых чисел. Предположим, что $p p ...p = an+ 1 (⋆). 1 2 k$

Без ограничения общности можно считать, что $n$ – простое число, ведь если $n= st,$ то можно заменить $n$ на $s,$ а $a$ — на $t a.$ Заметим, что $n> 2,$ поскольку $2 a + 1$ не делится на $3= p1$ при любом $a.$

Пусть у $a$ есть нечетный простой делитель $q.$ Тогда $q > pk,$ иначе левая часть $(⋆)$ делилась бы на $q,$ что не так. Поэтому и $a >pk.$

Покажем, что $n > pk.$ Действительно, в противном случае $n =pi,$ где $i≤ k.$ Тогда $p a i +1$ кратно $pi;$ с другой стороны, по малой теореме Ферма $p a i − a$ кратно $pi.$ Так как

api + 1= (a+1)(api−1− api−2+ ⋅⋅⋅− a+1),

причём $pi pi a +1 =(a +1)− (a − a)$ кратно $pi$ и

p−1 p−2 a i − a i + ⋅⋅⋅− a+ 1= 1+ 1+⋅⋅⋅+1= pi ≡ 0 (mod pi),

то $api + 1$ делится на $p2, i$ что противоречит условию.

Итак, $a >p k$ и $n> p, k$ откуда

n pk a + 1> pk > p1p2...pk

что противоречит $(⋆)$ , значит, $a$ — степень двойки. Степени двойки имеют остатки $1,2,4$ при делении на $7,$ а $an +1$ делится на $7$ при $k > 3.$ Значит, $k≤ 2,$ и возможными значениями для $an$ являются $3− 1= 2$ и $3⋅5− 1= 14.$ Оба варианта не подходят, следовательно, подходящих $k$ нет.

Ответ:

Таких $k$ не существует

Ошибка.
Попробуйте повторить позже

Задача 6#80974Максимум баллов за задание: 7

Для натурального $n$ обозначим $S =1!+ 2!+ ...+ n!. n$ Докажите, что при некотором $n$ у числа $S n$ есть простой делитель, больший $2012 10 .$

Источники: Всеросс., 2012, ЗЭ, 11.8(см. olympiads.mccme.ru)

Показать доказательство

Для простого $p$ и натурального $n$ обозначим через $v (n) p$ степень, в которой $p$ входит в разложение $n$ на простые множители. Заметим, что если $vp(n)⁄= vp(k)$ , то $vp(n ±k)= min(vp(n),vp(k)).$

Предположим противное, обозначим $2012 P = 10 .$ Тогда все простые делители чисел вида $Sn$ не превосходят $P.$

______________________________________________________________________________________________________________________________________________________

Лемма: Пусть $vp(Sn)< vp((n+ 1)!)$ при некотором $n.$ Тогда $vp(Sk) =vp(Sn)$ при всех $k≥ n.$

Доказательство: Обозначим $a= vp(Sn),b=vp((n +1)!),$ тогда $b ≥a+ 1.$ Заметим, что если $Sk = Sn+ (n+ 1)!+...+k!.$ В этой сумме все слагаемые, кроме первого, делятся на $a+1 p .$ а первое делится лишь на $a p .$ но не на $a+1 p .$ Значит и $Sk$ делится на $a p ,$ но не на $a+1 p .$

______________________________________________________________________________________________________________________________________________________

Рассмотрим некоторое простое $p≤ P.$ Ввиду леммы, если $vp(Sn)< vp((n+ 1)!)$ при некотором $n,$ то существует число $ap$ такое, что $vp(Sn) ≤ap$ при всех натуральных $n.$ Назовём такое простое число $p$ маленьким, все остальные простые числа, меньшие $P,$ назовём большими. Так как маленьких простых конечное количество, существует натуральное $M,$ большее любого числа вида $pap,$ где $p$ — маленькое.

Пусть теперь $p$ — большое простое число, а $n$ — такое число, что $p|n+ 2.$ Тогда из леммы имеем $vp(Sn+1)≥ vp((n +2)!)> vp((n+ 1)!),$ а это означает, что $vp(Sn)= vp(Sn+1− (n +1)!)= vp((n+ 1)!)=vp(n!).$ Последний переход верен, так как $n+ 1$ не кратно $p.$

Рассмотрим теперь $N = M ⋅P!− 2.$ По доказанному, $vp(SN)= vp(N!)$ для любого большого простого $p.$ Кроме того, поскольку $N ≥ M,$ то $vp(SN)≤ vp(pap)≤vp(N!)$ для любого маленького простого $p.$ Поскольку все простые делители числа $SN$ — либо большие, либо маленькие, отсюда следует, что $SN ≤ N!,$ что, очевидно, неверно. Противоречие.

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#75643Максимум баллов за задание: 7

На стороне $BC$ параллелограмма $ABCD$ ( $∠A < 90∘$ ) отмечена точка $T$ так, что треугольник $ADT$ — остроугольный. Пусть $O ,O 1 2$ и $O3$ — центры описанных окружностей треугольников $ABT,ADT$ и $CDT$ соответственно. Докажите, что точка пересечения высот треугольника $O1O2O3$ лежит на прямой $AD.$

Источники: Всеросс., 2011, ЗЭ, 11.2(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Иногда, чтобы проверить, что точка лежит на некоторой фиксированной прямой, достаточно показать, что она движется линейно, при линейном движении некоторого другого объекта. Что можно рассмотреть в качестве данного объекта в нашей задаче?

Подсказка 2

Сначала может показаться, что хорошей идеей является движение точки T вдоль прямой BC. К сожалению, при этом центр описанной окружности треугольника ATD не будет двигаться линейно, а значит последующее решение не предоставляется возможным. Что можно двигать линейно, чтобы исправить данную проблему?

Подсказка 3

Давайте будем двигать линейно отрезок BC вдоль прямой, на которой он лежит. Докажите, что каждый из центров окружностей так же будет двигаться линейно. Почему при этом ортоцентр будет двигаться линейно?

Подсказка 4

Высоты из точек O₁ и O₃ параллельны соответственно сторонам TD и AT, следовательно, ортоцентр является точкой пересечения прямых постоянного направления, проходящий через точки, которые движутся линейно. Таким образом, достаточно найти два положения, при которых ортоцентр лежит на прямой AD. Найдите их.

Подсказка 5

Что может быть лучше высот? Много высот! Рассмотрите положение отрезка BC, при котором ABCD является прямоугольником.

Подсказка 6

В качестве одного из возможных вторых положений можно рассмотреть такое, при котором B совпадает с точкой T. Помните, что если на описанной окружности треугольника выбрана точка, то ее образы при отражении относительно сторон треугольника попадают на одну прямую, которая проходит через ортоцентр треугольника.

Показать доказательство

$PIC$

Зафиксируем точки $A,D,T.$ Пусть точка $B$ движется линейно по прямой, проходящей через $T,$ параллельно $AD.$ Тогда точка $C$ так же движется линейно, поскольку $--- B+ AD = C.$ Кроме этого, $O1$ является точкой пересечения серединных перпендикуляров к отрезкам $AT$ (фиксирован при движении) и $BT$ (имеет постоянное направление и проходит через середину отрезка $BT,$ которая движется линейно), следовательно движется линейно. Аналогично точка $O3$ движется линейно.

Рассмотрим треугольник $O1O2O3.$ Заметим, что прямая $O1O2$ фиксированная, поскольку является серединным перпендикуляром к фиксированному отрезку $AT,$ следовательно высота, проведенная из точки $O3$ имеет постоянное направление, кроме этого проходит через линейнодвижущуюся точку. То же верно про высоту, проведенную из вершины $O1.$ Наконец, точка пересечения $H$ указанных прямых движется линейно. Покажем, что в двух положениях $H$ лежит на $AD.$

Положение 1. Пусть точка $B$ такова, что $ABCD$ является прямоугольником. Тогда $O1$ является серединой стороны $AT,O3$ — $DT.$ Пусть $M$ — середина стороны $AD.$ Как известно, $O2$ является ортоцентром треугольника $MO1O3,$ а значит $M$ является ортоцентром треугольника $O1O2O3$ и принадлежит $AD.$

Положение 2. Пусть $B$ совпадает с $T.$ В этом случае точка $O1$ определяется как точка пересечения прямой, проходящей через $T$ и перпендикулярной $AD,$ и серединного перпендикуляра к $AT,$ точка $O3$ симметрична $O2$ относительной прямой $TD.$

Заметим, что

∘ ∠O2O1T = 90 − ∠AT O1 = ∠A = ∠TO2O3 = ∠TO3O2

что влечет принадлежность точек $O1,O2,O3$ и $T$ одной окружности.

$PIC$

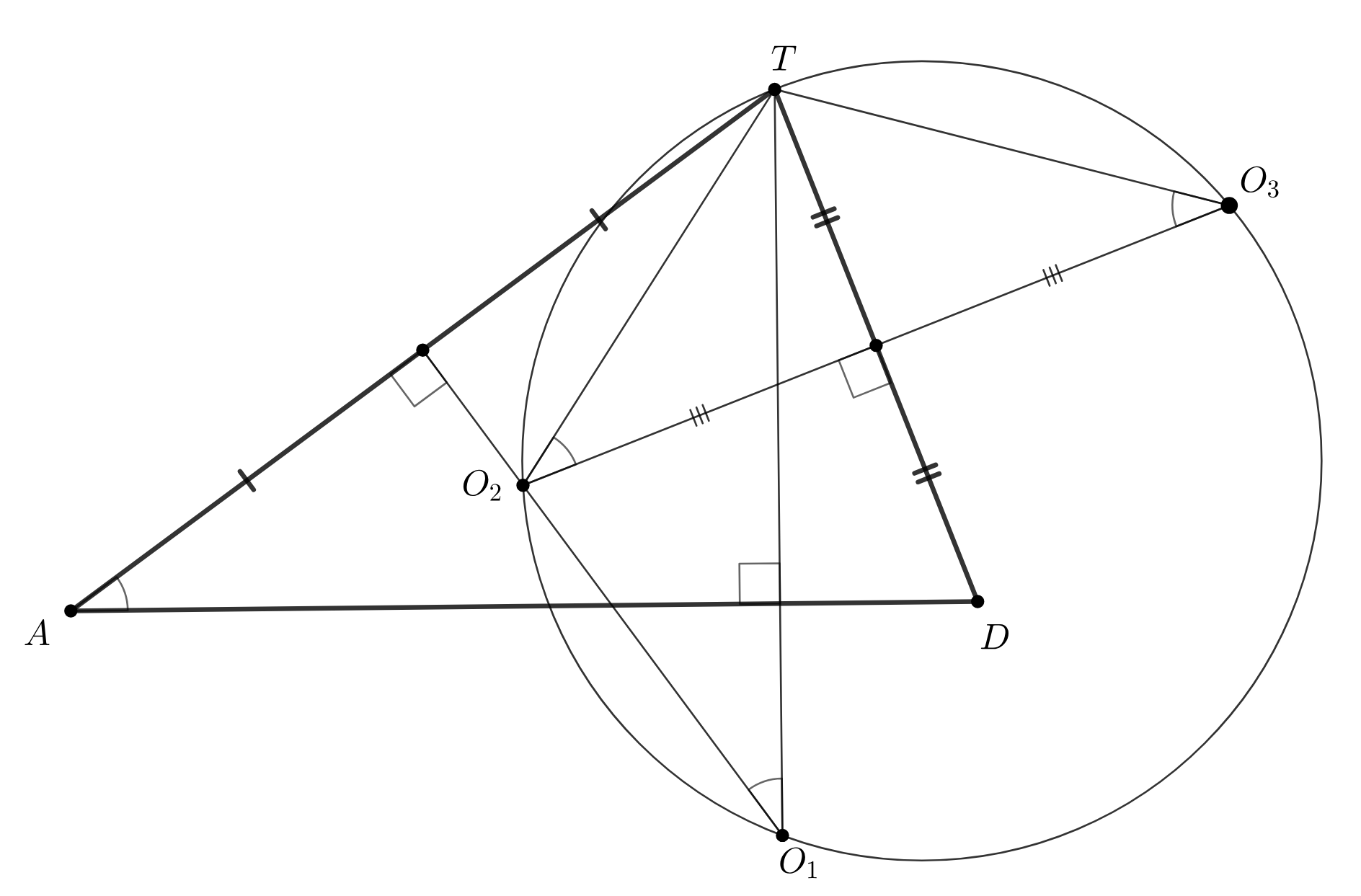
Наконец, точки $A$ и $D$ симметричны точке $T$ относительно одной из сторон треугольника $O1O2O3$ , следовательно прямая $AD$ является прямой Штейнера точки $T$ относительно треугольника $O1O2O3$ и проходит через ее ортоцентр.

Ошибка.
Попробуйте повторить позже

Задача 8#96642Максимум баллов за задание: 7

В клетчатой таблице $n ×n$ ( $n> 4)$ поставлены $n$ знаков “ $+$ ” в клетках одной диагонали и знаки “ $−$ ” во всех остальных клетках. Разрешается в некоторой строке или в некотором столбце поменять все знаки на противоположные. Докажите, что после любого количества таких операций в таблице останется не менее $n$ плюсов.

Источники: Всеросс., 2010, ЗЭ, 11.2(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Количество клеток, содержащих "+", было бы удобно оценивать, если бы нам удалось выделить множество клеток, среди которых в любой момент времени будет не меньше одного "+".

Подсказка 2

Покажите, что среди любых четырех клеток, которые образуют прямоугольник, в которых изначально было нечетное количество "+", в любой момент времени найдется клетка, которая содержит "+".

Подсказка 3

Выделите на исходной доске на такие непересекающиеся прямоугольники, каждый из которых содержит ровно одну клетку, выделенной диагонали (той, где изначально стоят "+").

Показать доказательство

Пронумеруем строки числами $1,...,n$ сверху вниз, а столбцы — теми же числами слева направо. Клетку будем обозначать парой номеров её строки и столбца; при этом будем считать, что клетки диагонали из плюсов имеют координаты $(i,i)(i= 1,...,n).$

Заметим, что если четыре клетки лежат в вершинах прямоугольника со сторонами, параллельными осям координат, то любая операция либо не меняет знаков в этих клетках, либо меняет знаки ровно в двух клетках из четырёх. В частности, чётность количества плюсов в этих четырёх клетках не меняется; значит, если среди них вначале был ровно один плюс, то и потом их будет не менее одного.

Теперь выберем в нашей таблице $n$ непересекающихся таких четвёрок; по сказанному выше, после любых операций в каждой из них найдётся как минимум один плюс, следовательно, всего плюсов будет не менее $n.$ При $i= 1,2,...,n− 2$ выберем четвёрку клеток выберем четвёрку клеток ${(i,i),(i,i+ 1),(i+2,i),(i+ 2,i+ 1)},$ а также выберем четвёрки ${(n − 1,n− 1),(n − 1,n),(1,n − 1),(1,n)}$ и ${(n,n),(n,1),(2,n),(2,1)}.$ Легко видеть, что они удовлетворяют всем требованиям. На рисунке отмечены такие четвёрки при $n =5.$

$PIC$

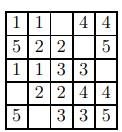
Ошибка.
Попробуйте повторить позже

Задача 9#94714Максимум баллов за задание: 7

На плоскости отмечены все точки с целыми координатами ( $x,y$ ) такие, что $x2+ y2 ≤ 1010$ . Двое играют в игру (ходят по очереди). Первым ходом первый игрок ставит фишку в какую-то отмеченную точку и стирает ее. Затем каждым очередным ходом игрок переносит фишку в какую-то другую отмеченную точку и стирает ее. При этом длины ходов должны все время увеличиваться; кроме того, запрещено делать ход из точки в симметричную ей относительно центра. Проигрывает тот, кто не может сделать ход. Кто из играющих может обеспечить себе победу, как бы ни играл его соперник?

Источники: Всеросс., 2009, ЗЭ, 11.4(см. math.ru)

Показать ответ и решение

Пусть игра с теми же правилами происходит на конечном множестве точек $S,$ которое содержит точку $O(0,0)$ и переходит в себя при повороте на $∘ 90 .$ Тогда в этой игре выигрывает первый игрок (ясно, что множество точек из условия удовлетворяет этим условиям).

Доказательство будем вести индукцией по количеству $n$ точек в $S.$ Если $n =1,$ то первый выигрывает первым своим ходом. Пусть $n >1.$ Теперь под отрезками будем подразумевать отрезки, концы которых лежат в $S$ и не симметричны относительно $O.$ Рассмотрим длины всех отрезков. Пусть $d$ — максимальная из них, и пусть $A1B1,A2B2,...,AnBn$ — все отрезки длины $d$ (некоторые из точек $Ai,Bj$ могут совпадать). Заметим, что точка $O$ не является концом ни одного из этих отрезков. Действительно, пусть это не так, и среди наших отрезков есть какой-то отрезок $OA.$ Пусть точка $B ∈ S$ получается из $A$ поворотом на $∘ 90$ относительно $O.$ Тогда $√- AB = 2OA >OA,$ то есть длина отрезка $OA$ не максимальна — противоречие.

Выкинем из $S$ все точки $Ai,Bi.$ Заметим, что полученное множество $S ′$ удовлетворяет всем условиям нашего утверждения (так как множество отрезков $AiBi$ переходит в себя при повороте на $90∘).$ Значит, по предположению индукции в игре на полученном множестве $S′$ выигрывает первый. Предъявим теперь выигрышную для него на множестве $S.$

Первый будет действовать по стратегии для множества $S′$ с начала до того момента, когда второй впервые выведет фишку за пределы множества $S′.$ Это случится, ибо согласно стратегии для $S′$ у первого всегда есть ход, после которого фишка остается в множестве $S′.$ Значит, рано или поздно второй сделает ход из точки $X,$ лежащей в $S′,$ в точку $Y,$ не лежащую там (пусть тогда $Y =Ai).$ Тогда первый может сделать ход в точку $Bi$ (так как $AiBi = d,$ а $XAi < d,$ иначе бы $X$ не лежала в $S′).$ после чего второму ходить некуда — он должен сделать ход длины, большей $d,$ а таких ходов нет. Итого, первый выигрывает.

Ответ:

Первый

Ошибка.
Попробуйте повторить позже

Задача 10#79802Максимум баллов за задание: 7

По окружности отметили $40$ красных, $30$ синих и $20$ зеленых точек. На каждой дуге между соседними красной и синей точками поставили цифру $1,$ на каждой дуге между соседними красной и зеленой — цифру $2,$ а на каждой дуге между соседними синей и зеленой — цифру $3.$ (На дугах между одноцветными точками поставили $0.$ ) Найдите максимальную возможную сумму поставленных чисел.

Источники: Всеросс., 2008, ЗЭ, 11.2(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Может перейти от чисел на дугах к числам в точках?

Подсказка 2

Возьмите веса: красная = 0, синяя = 1, зелёная = 2. Тогда для разноцветной дуги число равно сумме меток концов, а на одноцветной дуге число < сумм меток концов.

Подсказка 3

Как связана сумма чисел на всех дугах с суммой меток в точках?

Подсказка 4

Сумма по дугам ≤ 2·(сумма меток по точкам), так как каждая дуга сравнима с суммой меток концов, а одноцветная — строго меньше.

Подсказка 5

40·0 + 30·1 + 20·2 = 70, удвоив, получаем 140 — верхняя оценка суммы по дугам.

Подсказка 6

Достижима ли оценка 140? Стоит расположить точки, чтобы все дуги были разноцветными?

Показать ответ и решение

Поставим в каждой красной точке число $0,$ в каждой синей — $1,$ а в каждой зеленой — $2.$ Тогда каждое число на разноцветной дуге равно сумме чисел в ее концах, а каждое число на одноцветной дуге меньше суммы в ее концах. Значит, сумма чисел на дугах не превосходит удвоенной суммы чисел в точках, причем равенство достигается, когда все дуги — разноцветные. Сумма чисел в точках равна $40⋅0+ 30⋅1+20⋅2= 70,$ поэтому сумма чисел на дугах не больше $140.$

Осталось привести пример, когда эта оценка достигается (то есть когда все дуги разноцветны). Расставим сначала по кругу $40$ красных точек; затем вставим между соседними красными по точке другого цвета — $30$ синих и $10$ зеленых. Наконец, вставим оставшиеся $10$ зеленых на дуги между красными и синими точками (таких дуг образовалось $60,$ поэтому их хватит).

Ответ:

$140$

Ошибка.
Попробуйте повторить позже

Задача 11#106962Максимум баллов за задание: 7

Докажите, что при $k> 10$ в произведении

k f(x)= cos(x)cos(2x)cos(3x)...cos(2 x)

можно заменить один $cos$ на $sin$ так, что получится функция $f1(x),$ удовлетворяющая при всех действительных $x$ неравенству $|f1(x)|≤ -3--. 2k+1$

Источники: Всеросс., 2007, ЗЭ, 11.1(см. olympiads.mccme.ru)

Показать доказательство

Заметим, что

| 3 | | 2 | |sin3x|= |3sinx − 4sin x|= |3− 4sinx||sinx|≤ 3|sinx|

Поэтому для функции $f, 1$ полученной из $f$ заменой $cos3x$ на $sin 3x,$ выполняется неравенство

|| k|| |f1(x)|≤ 3|sin x||cosx||cos2x||cos4x||cos8x|...|cos2x|

(Мы опустили все множители $|cosnx|,$ в которых $n> 3$ и не является степенью двойки; каждый из этих множителей не превосходит $1.)$ Утверждение задачи теперь следует из тождества

sinxcosxcos2xcos4xcos8x...cos2kx= 2−k−1sin2k+1x

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#65466Максимум баллов за задание: 7

Существует ли ограниченная функция $f :ℝ → ℝ$ такая, что $f(1)> 0$ и $f(x)$ удовлетворяет при всех $x,y ∈ ℝ$ неравенству

2 2 2 f (x+ y)≥f (x)+2f(xy)+ f (y)?

Источники: Всеросс., 2005, ЗЭ, 11.5(см. math.ru)

Подсказки к задаче

Подсказка 1

В условии дано значение в единичке, быть может, попробуем воспользоваться им? Подставим x₁ и y₁ такие, чтобы в неравенстве из условия возникло f(1). Тогда можно будет получить некоторую цепочку неравенств.

Подсказка 2

Попробуем такие x₁ и y₁, что их произведение даёт единичку! Тогда мы сможем оценить разницу между f²(x₁+y₁) и f²(x₁).

Подсказка 3

Пусть a = f(1). Тогда разница между f²(x₁+y₁) и f²(x₁) выражается через a. А можно ли сделать её ещё больше?...Какие x₂ и y₂ можно для этого подобрать?

Подсказка 4

Запишите цепочку неравенств между значениями функции, где разница между двумя соседними будет хотя бы a.

Показать ответ и решение

Возьмём произвольно $x ⁄= 0 1$ и положим $y = 1- 1 x1$ . Тогда

2 2 2 2 f(x1+ y1)≥ f (x1)+ 2f(1)+f (y1)≥ f (x1)+ a (a= 2f(1)> 0)

Будем далее выбирать

-1 xn = xn−1+ yn− 1,yn = xn,n≥ 2

Тогда

f2(xn +yn)≥ f2(xn)+ a= f2(xn−1+ yn− 1)+ a≥ f2(xn−1)+ 2a ≥...≥f2(x1)+ na

Ясно, что последовательность $f(xi)$ неограниченна, что противоречит условию.

Ответ:

нет

Ошибка.
Попробуйте повторить позже

Задача 13#97454Максимум баллов за задание: 7

В прямоугольной таблице $9$ строк и $2004$ столбца. В её клетках расставлены числа от $1$ до $2004,$ каждое – по $9$ раз. При этом в каждом столбце числа различаются не более чем на $3.$ Найдите минимальную возможную сумму чисел в первой строке.

Источники: Всеросс., 2004, ЗЭ, 11.4(см. math.ru)

Показать ответ и решение

Переставив, если нужно, столбцы, будем далее считать, что числа в первой строке стоят в неубывающем порядке. Пусть $a i$ — $i−$ ое число первой строки. Рассмотрим сумму

S = (a1− 1)+(a2− 1)+ (a3 − 1)+ (a4− 2)+...+ (ai+(i− 2))+

+...+ (a2003− 2001)+(a2004− 2001)

Докажем, что $S ≥ 0.$ Пусть $i−$ е слагаемое этой суммы равно $di.$ Если в этой сумме нет отрицательных членов, все очевидно. Ясно, что $a2004 ≥ 2001,$ $a2 ≥ a1 ≥ 1,$ то есть $d1,d2,d2004 ≥ 0.$ Пусть $di <0,$ то есть $ai ≤i− 3.$ Тогда в первых $i$ столбцах содержатся только числа от $1$ до $i,$ следовательно, там содержатся все такие числа. Отсюда следует, что $ai =i− 3,ai+1 ≥ i+1$ и $di+di+1 > 0.$ Таким образом, для любого отрицательного $di$ сумма его со следующим членом положительна, поэтому, объединив такие слагаемые в пары, получаем сумму неотрицательных слагаемых. Итак,

a1+ a2+ ...+a2004 ≥1+ 1+ 1+ 2+...+2001+ 2001= 2005004

Это число достигается для таблицы, в которой первые три клетки первой строки заполнены единицами, а дальше идут числа $2,3,4...2000,2001,2001.$ Далее заполняем столбцы: в первом столбце все единицы, кроме последних двух ячеек, заполненных двойками. Во втором столбце после первой единицы стоят двойки во всех ячейках, кроме последних двух, заполненных тройками. После этого все столбцы, кроме последнего, заполняются по принципу: пусть в первой ячейке этого столбца стоит $k,$ тогда во всех остальных ячейках, кроме двух последних ставится $k +2,$ а в двух последних — $k+ 3.$ В последнем столбце 8 последних ячеек заполняются числом $2004.$

Ответ:

2005004

Ошибка.
Попробуйте повторить позже

Задача 14#76050Максимум баллов за задание: 7

В стране $100$ городов, некоторые пары городов соединены дорогами. Для каждых четырёх городов существуют хотя бы две дороги между ними. Известно, что не существует маршрута, проходящего по каждому городу ровно один раз. Докажите, что можно выбрать два города таким образом, чтобы каждый из оставшихся городов был соединен дорогой хотя бы с одним из двух выбранных городов.

Источники: Всеросс., 2003, ЗЭ, 11.7(см. math.ru)

Подсказки к задаче

Подсказка 1

Переведём задачку на язык графов. Города - вершины, дороги - рёбра, а как можно правильнее применить условия про отсутствие пути, проходящего через все города?

Подсказка 2

Верно, из этого следует, что самый длинный путь S соединяет не более 99 вершин. Давайте теперь немного изучим наш рисунок. Например, могут ли крайние вершины пути быть смежными? А что можно сказать о смежности вершин пути S с вершинами вне этого пути?

Подсказка 3

Конечно, получается, с вершинами не из S могут соединяться только те, что не стоят на концах S (и только если путь не замыкается в цикл). Но ведь у нас также есть правило про 2 ребра на 4 вершины. Что, если две из них принадлежат S, а две - не принадлежат?

Подсказка 4

В предыдущем рассмотрении мы не учли, что существуют случаи, когда взять какие-то 2 вершины не из S невозможно. Это происходит, когда в S ровно 99 вершин. Здесь уже нельзя сразу сделать вывод о смежности концов пути, так что лучше будет отдельно разобрать два случая.

Подсказка 5

В случае, когда образуется цикл из вершин S и вершина вне него не соединяется ни с одной вершиной цикла, обратите внимание на то, сколько рёбер могут отсутствовать в подграфе S. Что можно сказать об их чётности? Что из этого следует?
Осталось только рассмотреть случай, когда вершины концов S несмежны и отдельная вершина смежна хотя бы с одной вершин пути. Тут стоит вспомнить, что при проведении рёбер не должен получиться путь, соединяющий все 100 вершин. Остаётся только проверить, возможно ли это в сочетании с условием про два рёбра.

Показать доказательство

Построим граф, вершины которого соответствуют городам, а ребра — дорогам. Выберем в этом графе самый длинный путь $S,$ пусть вершины $A$ и $B$ — концы этого пути. Из условия задачи следует, что в пути $S$ не более $99$ вершин. Отметим, что концы пути $S$ — вершины $A$ и $B−$ не могут быть смежны с вершинами не из $S$ (иначе путь можно удлинить). А в случае, когда вершины $A$ и $B$ смежны и наш путь замыкается в цикл, никакая вершина пути $S$ по аналогичным причинам не может быть смежна с вершиной не из $S.$

1) Рассмотрим случай, когда в $S$ не более $98$ вершин. В этом случае рассмотрим любые две вершины $Y1$ и $Y2,$ не входящие в путь $S,$ и концы пути $A$ и $B.$ Среди этих четырех вершин должны быть проведены хотя бы два ребра. Так как ни $A,$ ни $B$ не могут быть смежны с вершинами не из $S,$ то концы пути $A$ и $B$ соединены ребром.

Таким образом, путь $S$ замыкается в цикл, и тогда ни одна из вершин пути $S$ не смежна с вершиной не из $S.$ Рассмотрим четверку из любых двух вершин $X1$ и $X2$ пути $S$ и любых двух вершин $Y1$ и $Y2,$ не входящих в $S.$ Так как между этими четырьмя вершинами проведено хотя бы два ребра, то одно из них соединяет $X1$ и $X2,$ а другое — $Y1$ и $Y2.$ Таким образом, в рассматриваемом случае все вершины пути $S$ попарно смежны и все вершины не из $S$ также попарно смежны. Отсюда очевидно следует утверждение задачи. 2) Рассмотрим случай, когда вне пути $S$ лежит ровно одна вершина. Пусть это вершина $D.$ Если $D$ не смежна ни с одной из вершин пути $S,$ то рассмотрим $D$ и любые три вершины пути $S.$ Поскольку среди этих четырех вершин проведено хотя бы два ребра, то среди любых трех вершин пути $S$ проведено хотя бы два ребра. Следовательно, для любой вершины из $S$ есть не более одной не смежной с ней вершины пути $S.$ Поскольку $99$ вершин пути $S$ нельзя разбить на пары не соединенных ребром, то в $S$ должна быть вершина, смежная со всеми остальными вершинами $S.$ Эта вершина в паре с $D$ удовлетворяет утверждению задачи.

Если концы максимального пути $A$ и $B$ смежны, то, как мы доказали, вершина $D$ не смежна ни с одной из вершин пути $S,$ а этот случай уже разобран.

Остается рассмотреть последний случай, когда концы пути $S$ не смежны и вершина $D$ смежна хотя бы с одной из вершин пути $S.$ Рассмотрим вершины $A,B,D$ и произвольную четвертую вершину $Z$ (естественно, лежащую на пути $S$ ). Так как $A,B$ и $D$ попарно не смежны, то $Z$ смежна хотя бы с двумя вершинами из $A,B$ и $D.$ Пусть $D$ смежна с вершиной $X$ пути $S.$ Одна из соседних с $X$ вершин пути $S$ не является концом пути. Можно считать, что это первая вершина $Y,$ лежащая на пути из $X$ в $B$ по ребрам $S.$ Если $Y$ смежна с $D,$ то, пройдя от $A$ к $X$ по пути $S,$ далее по ребрам $XD$ и $DY$ и затем по пути $S$ от $Y$ к $B,$ мы обойдем все вершины нашего графа ровно по одному разу, что невозможно по условию. Если же $Y$ не смежна с $D,$ то, как мы доказали, эта вершина смежна и с $A,$ и с $B.$ Тогда пройдем по ребру $DX,$ далее по пути $S$ от $X$ к $A,$ по ребрам $AY$ и $YB,$ и затем по пути $S$ от его конца $B$ до вершины, соседней с $Y$ на пути $S,$ — получился путь, проходящей по каждой вершине нашего графа ровно один раз, которого по условию не существует. Следовательно, и этот случай не возможен.

Таким образом, мы рассмотрели все случаи и в тех из них, которые возможны, убедились в справедливости утверждения задачи.

Ошибка.
Попробуйте повторить позже

Задача 15#122866Максимум баллов за задание: 7

У Ани и Бори было по длинной полосе бумаги. На одной из них была написана буква А, на другой — Б. Каждую минуту один из них (не обязательно по очереди) приписывает справа или слева к слову на своей полосе слово с полосы другого. Докажите, что через сутки слово с Аниной полосы можно будет разрезать на $2$ палиндрома (то есть слова, читающихся одинаково слева направо и справа налево), один из которых может быть пустым.

Показать доказательство

Назовем планируемом слово, читающееся одинаково слева направо и справа налево. Докажем индукцией по $n,$ что через $n$ минут слово на любой полосе можно будет разрезать на два палиндрома (один из которых, возможно, пустой). Тогда, если эти палиндромы поменять местами, получится то же слово, записанное в обратном порядке.

Например, для $n =1$ утверждение, очевидно, верно. Пусть для $n − 1$ оно уже доказано. Рассмотрим слово $A$ на полосе. Пусть после первой минуты написано слово $A$ и $AB.$ Посадим Антона и Бориса в этот момент за полосом, на котором написаны буквы $A$ и $B,$ и попросим их повторять действия Анны и Бориса (т.е. если Анна приписывает букву $B$ к слову, то Антон приписывает $B$ к своему слову, и т.п.). Получившийся процесс длится $n − 1$ минуту. Тогда в конце процесса слова Антона и Бориса можно разрезать на два палиндрома каждое, а если в них заменить каждую букву $B$ на $AB,$ то получатся слова Анны и Бориса.

Докажем, что если к палиндрому из букв $A$ и $B$ приписать в конце $A$ и заменить каждую букву $B$ на $AB,$ то получится палиндром. Действительно, пусть перед первой $B$ стоит $x0$ букв $A,$ между первой и второй — $x1,$ после последней, $k$ -й буквы $B$ — $xk$ букв $A.$ Тогда $xi =xk−i$ при любом $1≤ i≤k.$ В измененном слове перед первой буквой $B$ будет $x0+ 1$ букв $A,$ между первой и второй — $x1+1,$ после последней, $k$ -й буквы $B$ — $xk+ 1$ букв $A.$ Поскольку $xi = xk−i,$ то полученное слово также будет палиндромом.

Пусть, скажем, Антоново слово из букв $A$ и $B$ разрезается на палиндромы $S$ и $T.$ Пусть $S′$ и $T′$ — слова, полученные заменой $B$ на $AB.$ Если слово $T$ непусто, то $S′A$ и $T′A$ — палиндромы, слово $T$ начинается с $A$ $(T′A = AT′′A),$ и поэтому $T′′$ — тоже палиндромом. Тогда Антоново слово разрезается на палиндромы $S′A$ и $T ′′.$ Если же слово $T$ пусто, то $S′A ∕S′$ ( $S′$ — палиндром) является требуемым разбиением. Доказательство для Борисового слова аналогично.

Ошибка.
Попробуйте повторить позже

Задача 16#97376Максимум баллов за задание: 7

На плоскости отмечено несколько точек. Для любых трех из них существует декартова система координат (т.е. перпендикулярные оси и общий масштаб), в которой эти точки имеют целые координаты. Докажите, что существует декартова система координат, в которой все отмеченные точки имеют целые координаты.

Источники: Всеросс., 2002, ЗЭ, 11.2(см. math.ru)

Подсказки к задаче

Подсказка 1

Есть подозрение, что n точек в задаче просто так. Предлагается для начала научиться понимать, почему для четырех точек существует нужная система координат. Как потом добавить в нее все оставшиеся точки?

Подсказка 2

Как подступиться к задаче? Введите в системы координат для точек A, B, C и B, C, D. У них есть общие 2 точки с целыми координатами, поэтому отношение квадратов единиц измерения рационально. Как теперь искать общую систему координат?

Подсказка 3

Получите, что (BC, BD) и (BA, BD) рациональны, после этого у вас будут два каких-то выражения. Выразите из них координату точки D. Докажите, что если она рациональна, то вы решили задачу!

Показать доказательство

Рассмотрим любые $3$ точки $A,B$ и $C,$ не лежащие на одной прямой (если все точки будут лежать на одной прямой, то утверждение задачи очевидно). Пусть $T1$ — система координат, в которой эти точки имеют целые координаты.

Рассмотрим любую из оставшихся точек, назовем ее $D.$ Пусть $T2$ — система координат, в которой точки $B,C,D$ имеют целые координаты. Поскольку квадрат длины отрезка $BC$ в $T1$ и $T2$ будет целым, то отношение квадратов единиц измерения $T1$ и $T2$ — рациональное число. Но скалярное произведение векторов $(−−→ −−→ ) BC,BD$ в $T2$ — целое, значит, в $T1$ оно рационально, поскольку произведение длин этих векторов в $T1$ будет рационально относиться к произведению их длин в $T2,$ а косинус угла не изменится.

Аналогично, $−→ −−→ (BA,BD )$ рационально. Пусть $−−→ BC$ в $T1−$ это $−→ (x,y),BA −$ это $−−→ (z,t),BD−$ это $(p,q).$ Тогда $px+qy =m$ и $pz+ qt=n−$ рациональны, откуда $p= mxLi−−ynzyz,q = nxc−Im−zyz-−$ рациональные числа (поскольку $xt− yz ⁄=0,$ так как $A,B,C$ не лежали на одной прямой). Следовательно, точка $D$ в $T1$ имеет рациональные координаты. Тогда, выбрав другую единицу измерения, можно координаты всех точек сделать целыми.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#81320Максимум баллов за задание: 7

Дана клетчатая доска $100× 100.$ Клетки доски покрашены в $4$ цвета так, что в каждой строке и в каждом столбце ровно $25$ клеток каждого цвета. Докажите, что найдутся $2$ строки и $2$ столбца, клетки на пересечении которых окрашены в $4$ различных цвета.

Источники: Всеросс., 2000, ЗЭ, 11.8(см. math.ru)

Показать доказательство

Предположим противное: пусть среди четырёх клеток на пересечении любых двух строк и любых двух столбцов есть две клетки одинакового цвета.

Назовём горизонтальной (вертикальной) парой две клетки разного цвета, лежащие в одной строке (одном столбце). Назовём горизонтальным (вертикальным) совпадением две клетки одинакового цвета, лежащие в одной строке (одном столбце). Разделим пары на 6 типов по цветам входящих в них клеток: ${1,2},{1,3},...,{3,4}.$

Рассмотрим две произвольные строчки. Из предположения следует, что каждые две вертикальных пары с клетками в этих строчках должны иметь общий цвет. Тогда в двух рассматриваемых строчках могут быть вертикальные пары не более, чем трех типов, причем возможны только два принципиально различных случая: все пары содержат один и тот же цвет (скажем, $1)$ или есть пары типов ${1,2},{1,3}$ и ${2,3}$ (или точно так же с другой тройкой цветов). Рассмотрим эти два случая.

Если все пары в наших двух строчках содержат клетку цвета $1,$ то всего пар не более, чем клеток цвета $1$ в обеих строчках, то есть не более $50.$ Значит, в рассматриваемых двух строчках не менее $50$ совпадений.

Пусть есть пары типов ${1,2},{1,3}$ и ${2,3}.$ В этом случае все клетки цвета $4$ в наших строчках совпадают, таким образом, есть не менее $25$ совпадений.

Итак, мы доказали, что в каждой паре строчек не менее $25$ вертикальных совпадений. Аналогичный результат верен и для любой пары столбцов. Таким образом, всего в нашем квадрате есть не менее $25⋅100⋅99$ совпадений. Но так как в каждой строке и в каждом столбце по $25$ клеток каждого цвета, количество совпадений равно $100⋅25⋅24⋅4= 24 ⋅1002.$ Учитывая, что $25⋅99> 24⋅100,$ приходим к противоречию.

Ошибка.
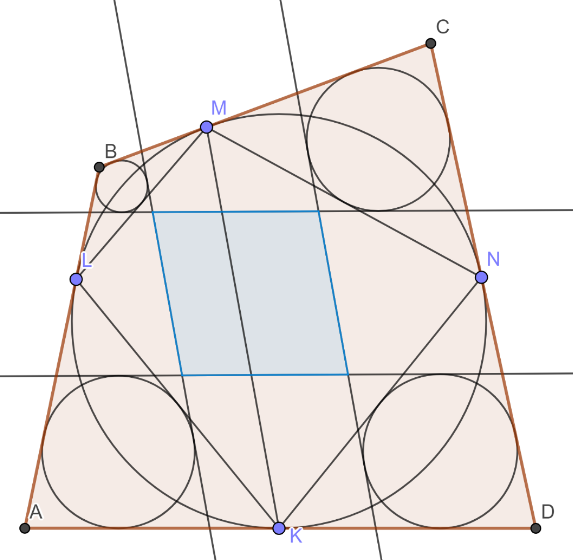
Попробуйте повторить позже

Задача 18#94740Максимум баллов за задание: 7

Окружность, вписанная в четырёхугольник $ABCD,$ касается его сторон $DA,$ $AB,$ $BC$ и $CD$ в точках $K,$ $L,$ $M$ и $N$ соответственно. Пусть $S1,$ $S2,$ $S3$ и $S4$ – окружности, вписанные в треугольники $AKL,$ $BLM,$ $CMN$ и $DNK$ соответственно. К окружностям $S1$ и $S2,$ $S2$ и $S3,$ $S3$ и $S4$ , $S4$ и $S1$ проведены общие касательные, отличные от сторон четырёхугольника $ABCD.$ Докажите, что четырёхугольник, образованный этими четырьмя касательными, – ромб.

Источники: Всеросс., 1999, ЗЭ, 11.3(см. math.ru)

Показать доказательство

Цетры окружностей $S 1$ и $S 2$ обозначим $I a$ и $I , b$ также за $I$ обозначим центр окружности, вписанной в треугольник $KLM.$ Отметим, что треугольники $KAL$ и $LBM$ равнобедренные, потому $KIa = LIa$ и $LIb = MIb.$ Тогда, поскольку точки $Ia$ и $Ib$ лежат на окружности, описанной около треугольника $KLM,$ тройки точек $K,I,Ib$ и $M,I,Ia$ лежат на прямых. Угол $∠IMIb$ равен половине дуги $IaIb$ (содержащей точку $L),$ в свою очередь дуга $IaIb$ равна сумме дуг $IaL$ и $LIb.$ Дуги $IaL$ и $LIb$ соответственно равны дугам $KIa$ и $IbM,$ полусумма которых равна углу $∠MIIb.$ Итак, $∠IMIb =∠MIIb.$ Опустим из $Ib$ перпендикуляры $IbH$ и $IbT$ на $LM$ и на касательную к $S2$ из $I.$ Тогда $IbH = IbT,$ также из доказанного ранее равенства углов следует $IbI = IbM,$ тогда прямоугольные треугольники $IbHM$ и $IbTI$ равны, а значит, $∠IbMH = ∠IbIT,$ тогда и $∠TIM = ∠HMI.$ Так как $MI$ биссектриса $△KLM,$ $∠IMK = ∠MIT.$ Итак, мы доказали, что касательная из $I$ к $S2$ параллельна $KM,$ аналогичными рассуждениями можно доказать и что касательная из $I$ к $S1$ параллельна $KM,$ тогда общая касательная к $S1$ и $S2$ из условия и есть касательная из $I,$ причём она параллельна $KM.$

$PIC$

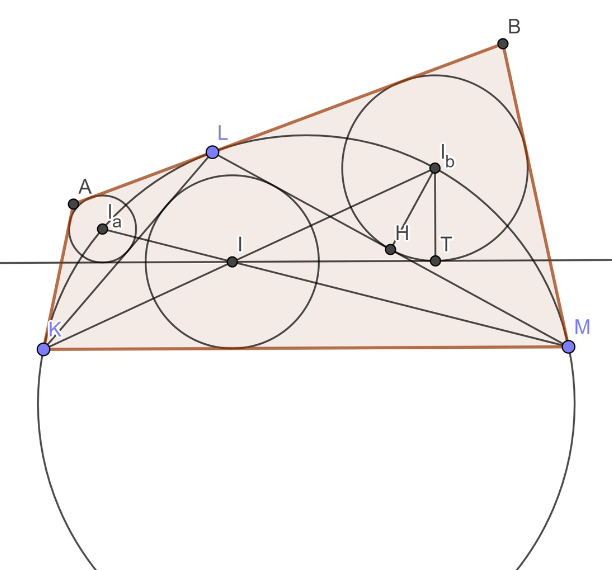
Также можно доказать и что общая касательная к $S3$ и $S4$ параллельна $KM,$ и что общие касательные к $S2$ и $S3,$ $S4$ и $S1$ параллельны $LN.$ Так, наш образовавшийся при пересечениях касательных четырёхугольник является параллелограммом. Осталось отметить, что его соседние стороны равны из свойства касательных и описанности четырёхугольника $ABCD.$

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 19#102033Максимум баллов за задание: 7

Через вершину $A$ тетраэдра $ABCD$ проведена плоскость, касательная к описанной около него сфере. Докажите, что линии пересечения этой плоскости с плоскостями граней $ABC,$ $ACD$ и $ABD$ образуют шесть равных углов тогда и только тогда, когда $AB ⋅CD = AC ⋅BD = AD ⋅BC.$

Подсказки к задаче

Подсказка 1

Задача прям и намекает рассмотреть проекцию картинки на плоскости ABC, ACD и ABD. Что получается при проекциях? Выпишите какие-то равенства. Как их связать с вопросом задачи?

Подсказка 2

В сечениях образуется касательная к окружности, у такой прямой понятное направление, поэтому разумно провести плоскость, параллельную касательной плоскости и пересекающую грани тетраэдра, тогда получаются вписанности. Что вы можете сказать про три точки пересечения плоскости с ребрами?

Подсказка 3

Докажите, что тождество из вопроса задачи и равенство углов из условия равносильны правильности треугольника в сечении параллельной плоскостью. Для этого вам может помочь степень точки или подобие.

Показать доказательство

Проведем плоскость, параллельную касательной плоскости, пересекающую ребра $AB,$ $AC$ и $AD$ в точках $B , 1$ $C 1$ и $D 1$ соответственно.

Рассмотрим плоскость $ABC.$ Заметим, что $∠ABC = ∠CAM$ (по теореме об угле между касательной и хордой), а $∠CAM = ∠AC1B1$ (как накрест лежащие при параллельных и секущей), т. е. $∠ABC =∠AC1B1.$ Следовательно, $△AB1C1 ∼ △ACB.$

$PIC$

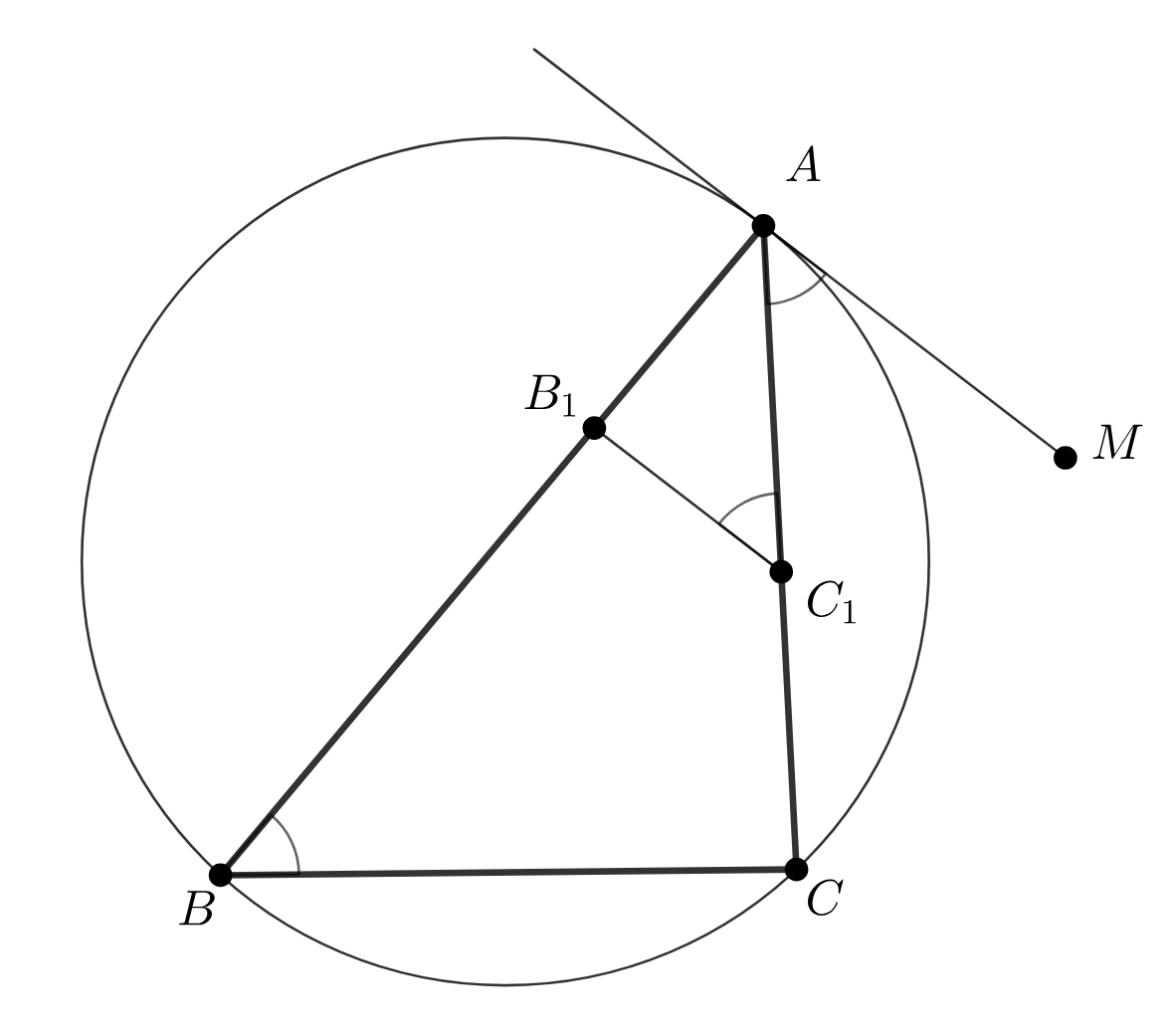
Откуда

B1C1= AB1-= AC1- BC AC AB

Аналогично,

C1D1-= AC1-= AD1; B1D1-= AD1-= AB1- CD AD AC BD AB AD

Из этих равенств вытекает, что

-CD1--- -AD1--- --AB1-- --AB1-- --AB1-- AB⋅CD = AB⋅AC = AD ⋅AC = AD ⋅BC = AB ⋅BC

Значит, $△A1B1C1$ равносторонний тогда и только тогда, когда

AB ⋅CD =AC ⋅BD = AD ⋅BC

Осталось заметить, что углы, образуемые указанными в условии линиями пересечения, соответственно равны углам треугольника $A1B1C1.$

Ошибка.
Попробуйте повторить позже

Задача 20#79220Максимум баллов за задание: 7

Внутри параболы $y = x2$ расположены несовпадающие окружности $ω ,ω ,ω ,... 1 2 3$ так, что при каждом $n >1$ окружность $ω n$ касается ветвей параболы и внешним образом окружности $ωn−1.$ Найдите радиус окружности $ω1998,$ если известно, что диаметр $ω1$ равен $1$ и она касается параболы в ее вершине.

Источники: Всеросс., 1998, ЗЭ, 11.5(см. math.ru)

Показать ответ и решение

Первое решение.

Посмотрим, при каких условиях окружность касается параболы. Пусть есть окружность радиуса $R1$ с центром в точке $A,$ а $B$ — точка касания окружности и параболы. Проведем касательную $BE.$ Тогда $∘ ∠ABE = 90$

$PIC$

Проведём через точку $B$ прямую, параллельную оси $Ox$ $(C$ — точка пересечения прямой и оси $Oy).$

Тогда $∠CBA +∠EBC1 = 90∘.$

Получаем, что $tg∠EBC1 = ctg∠ABC,$ но $tg∠EBC1 = 2x1$ , так как $EB$ — касательная $y = x2$ в точке $x1.$

Значит,

CB-=2x1 =⇒ AC = 1 AC 2

Тогда по теореме Пифагора получаем, что

2 2 1 R1 = x1+ 4

Теперь рассмотрим случай с двумя окружностями.

$PIC$

Пусть $CB =x1$ и $C1B1 = x2.$ Тогда

2 2 ( 2 1) ( 2 1) 2 2 R2− R1 = x2+ 4 − x1+ 4 = x2− x1 (1)

Также знаем, что

R2+ R1 = CC1 =x22− x21 (1)

Из $(1)$ и $(2)$ получаем, что $R2− R1 = 1$ .

То есть мы поняли, что если есть две окружности радиуса $R2$ и $R1$ соответственно, которые касаются параболы и друг друга, то их радиусы отличаются на $1$ .

Тогда получается, если $1 Rw1 = D∕2= 2,$ то

1 1 Rw2 = 1+ 2,...,Rw1998 = 1998− 1+ 2 = 1997,5

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть $rn$ — радиус $n$ -й окружности, $Sn = r1+r2+ ...+ rn.$ Тогда уравнение $(n +1)$ -й окружности имеет вид:

x2+ (y− (2Sn+ rn+1))2 = r2n+1 (1)

Условие касания означает то, что уравнение $(1)$ имеет один корень, тогда его дискриминат $D = (2rn+1− 1)2− 8Sn$ равен нулю, то есть $√--- rn+1 =-8Sn-+1 2$ (так как $rn+1 >0).$ Отсюда