03 Динамика
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Человеку массой требуется подтянуть к стене ящик массой
с помощью каната, перекинутого через блок. Если человек
стоит на горизонтальном полу, то для достижения цели ему нужно тянуть канат с минимальной силой
Н (см. рисунок). С
какой минимальной силой
придётся тянуть этому человеку канат, если он упрётся в ящик ногами? Части каната, не
соприкасающиеся с блоком, горизонтальны. Массами блока и каната пренебречь. Какие законы Вы используете для решения
задачи? Обоснуйте их применение.

Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Тела движутся поступательно, поэтму будем считать их материальными точками
3. Так как тела являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Так как блок и нить идеальные, то сила натяжения нити всюду одинакова
Решение
Сделаем рисунок с изображением сил.
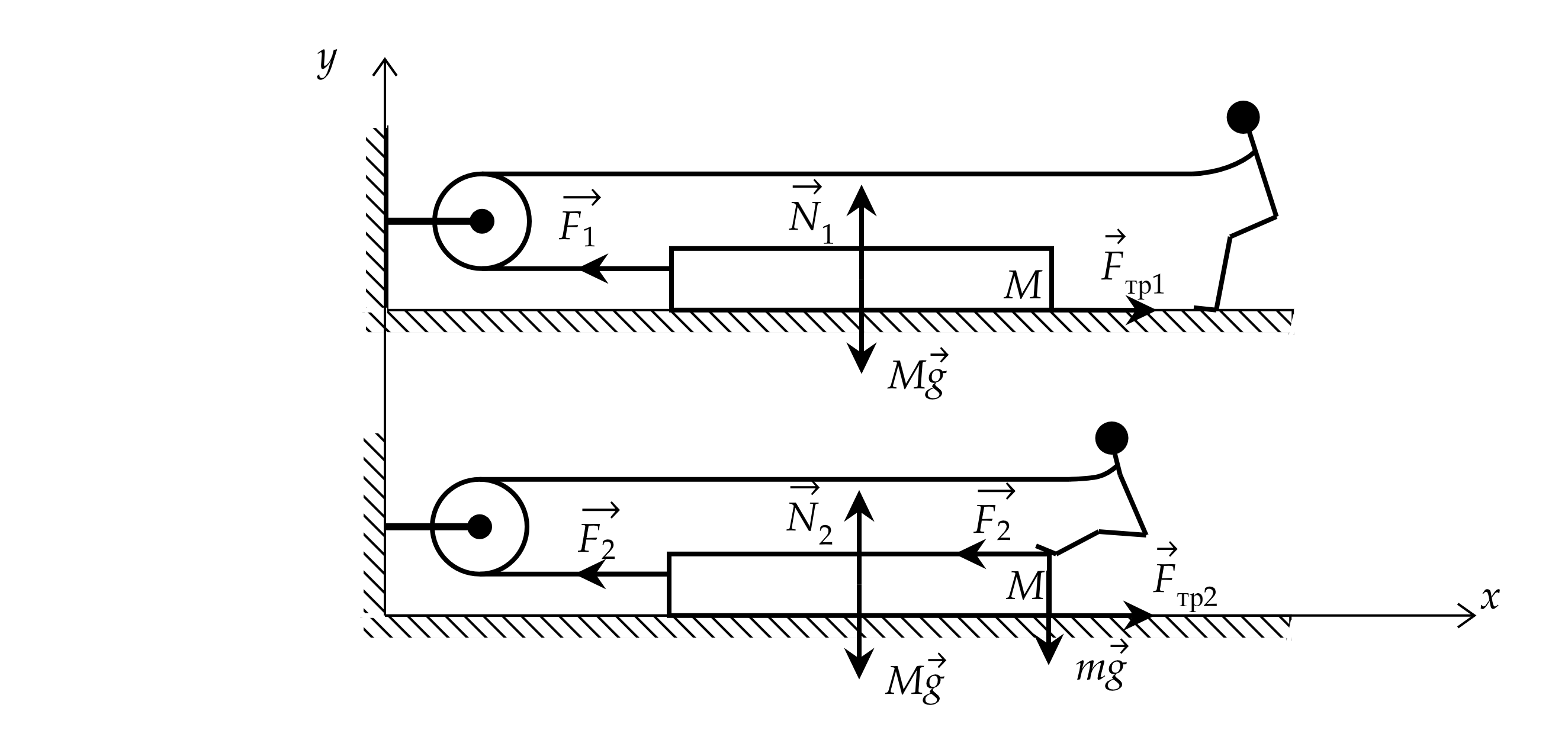
Запишем второй закон Ньютона для первого случая:
где – сила реакции опоры,
– сила трения,
– ускорение ящика.
Минимальность силы будет при
. Сила трения же равна:
где – коэффициент трения между ящиком и столом.
Спроецируем второй закон Ньютона на оси и
:
|
|
Отсюда
Запишем второй закон Ньютона для второго случая:
где – сила реакции опоры,
– сила трения,
– ускорение ящика с человеком.
Минимальность силы будет при
. Спроецируем второй закон Ньютона на оси
и
:
|
|
Отсюда
С учётом (1)
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение законов Ньютона для описания движения тел
4. Обосновано равенство сил натяжения нити
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на координатную ось, формула силы трения скольжения, записано условие при котором
требуемая сила будет минимальна).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Систему из бруска массой и доски массой
, находящихся на горизонтальном столе, приводят в движение,
прикладывая к доске горизонтальную силу
(см. рис.). Коэффициент трения между столом и доской и между горизонтальной
поверхностью доски и бруском равен
. Массой горизонтально натянутой нити, массой блока и трением в его оси
пренебречь.
1) Найти ускорение доски, если бы не было трения.
2) Найти ускорение доски, если есть трение и параметры
,
,
подобраны так, что есть движение.
1) Укажем силы, действующие на брусок (красным) и на доску (синим) для двух случаев.
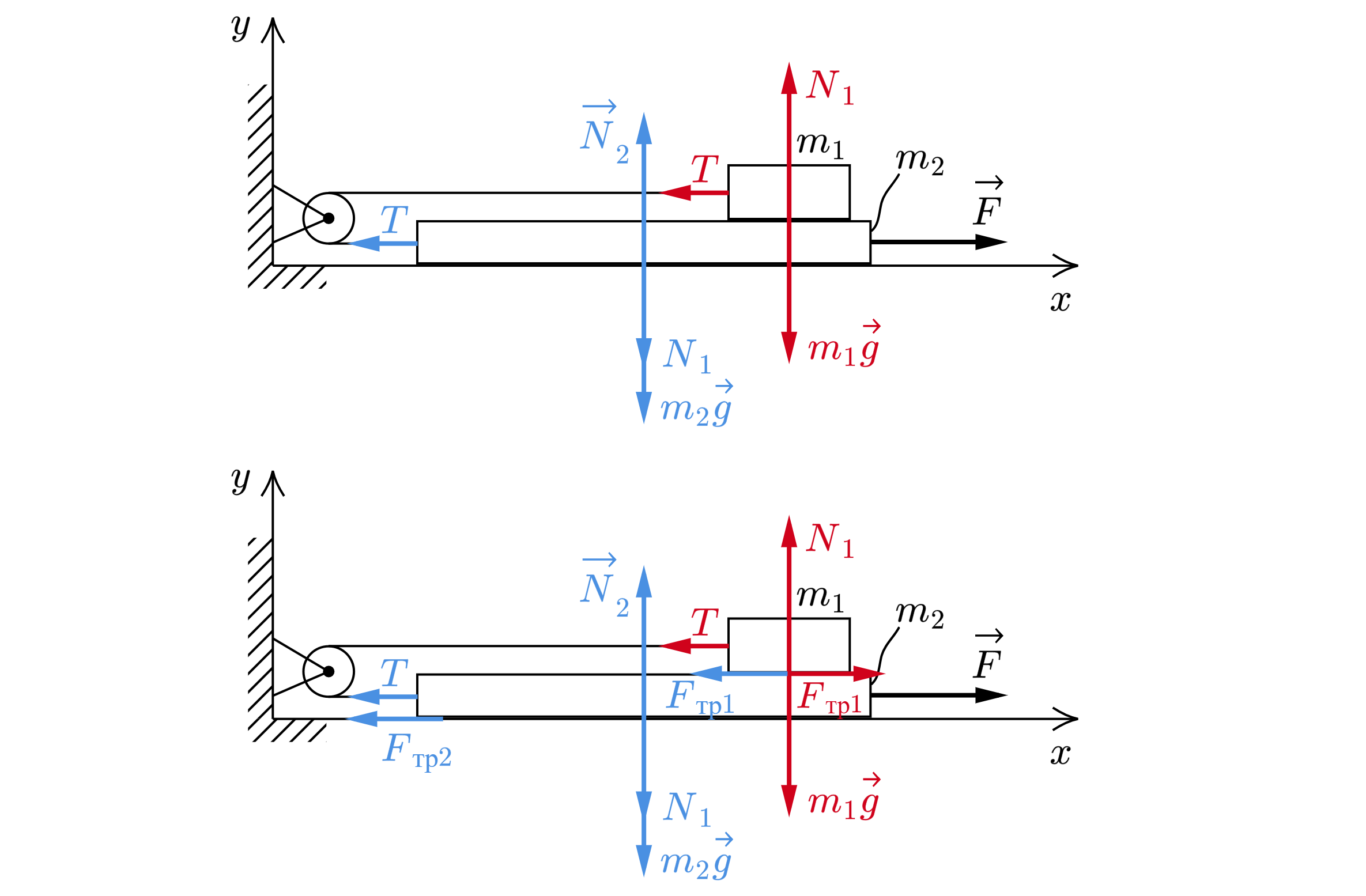
Так как нет силы трения (см. левый рисунок), то по второму закону Ньютона для бруска и доски
Ускорения тел равны из-за нерастяжимости нити. Спроецируем второй закон Ньютона на горизонтальную ось
|
|
откуда ускорение в первом случае
2) Запишем второй закон Ньютона для бруска и доски во втором случае
Сила трения равна:
Спроецируем второй закон Ньютона на вертикальную ось:
Спроецируем второй закон Ньютона на горизонтальную ось, с учётом (1):
|
|
Откуда
Ошибка.
Попробуйте повторить позже
Систему из груза массой бруска массой
и доски массой
удерживают в покое (рис.). Брусок находится на
расстоянии
от края доски. Систему отпускают и брусок движется по доске, а доска – по горизонтальной
поверхности стола. Коэффициент трения скольжения между бруском и доской
а между доской и столом
1) Определить ускорение бруска относительно стола при движении бруска по доске?
2) Через какое время брусок достигнет края доски? Считать, что за время опыта доска не достигает блока. Массу нити,
блока и трение в оси блока не учитывать.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Груз и брусок движутся поступательно, поэтому их можно считать материальными точками.
3. Так как груз и брусок являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Учитывая, что нить нерастяжима, делаем вывод, что связанные тела движутся с одинаковым ускорением.
5. Учитывая, что нить невесома и блок идеальный, делаем вывод, что силы натяжения, приложенные к телам, равны по модулю.
Решение
Расставим силы, действующие на груз (черный цвет), брусок (красный) и доску (синий).
Ускорение бруска и груза равны из-за нерастяжимости нити. Запишем второй закон Ньютона для груза, бруска и доски:
Спроецируем второй закон на оси и
:
|
|
|
|
Из второй системы
|
|
Сила трения же равна:
Тогда
|
|
1) Имеем систему уравнений:
|
|
Отсюда
2) Найдём также ускорение доски:
Значит, доска движется влево с ускорением . Тогда брусок движется по доске с ускорением:
Путь бруска по доске находится по формуле:
где – начальная скорость,
– время движения.
Так как система изначально покоилась, то и
отсюда искомое время:
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность испольования законов | 1 |
| (закономерностей). В данном случае: выбор ИСО, модель материальной точки, равенство модулей сил натяжения нитей и модулей ускорений брусков, возможность применения второго закона Ньютона | |
| В обосновании возможности использования законов | 0 |
| (закономерностей) допущена ошибка | |
|
ИЛИ
| |
| Обоснование отсутствует | |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае - второй закон Ньютона, формула силы трения скольжения, формулы кинематики равноускоренного движения); | |
| II) описаны вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений величин, используемых | |
| в условии задачи, и стандартных обозначений величин, | |
| используемых при написании физических законов); | |
| III) проведены необходимые математические преобразования | |
| и расчёты (подстановка числовых данных в конечную формулу), | |
| приводящие к правильному числовому ответу (допускается решение | |
| «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| фиизческой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| фиизческие законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков. | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И(ИЛИ)
| |
| В решении имеются лишние записы, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения и не | |
| зачёркнуты | |
|
И(ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и(или) в математических преобразованиях/ | |
| вычислениях пропущены логически важные шаги. | |
|
И(ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе | |
| в записи единиц измерений величины) | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| данной задачи, без каких-либо преобразований с их | |
| использованием, направленных на решение задачи. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения данной задачи (или утверждение, лежащее в основе | |
| решения), но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения данной | |
| задачи (или в утверждения, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Система из двух грузов, соединенных пружиной жесткости Н/м движется под действием груза
кг по наклонной
плоскости с углом наклона 30 градусов так, что длина пружины
не меняется. В нерастянутом состоянии длина пружины
см. Массы маленьких грузов одинаковы и равны
кг. Найдите длину пружины
. Трением пренебречь. Нить невесома и
нерастяжима, а блок идеальный.
Какие законы Вы используете для описания движения грузов? Обоснуйте их применение к данному случаю.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Все три тела движутся поступательно, поэтому их можно считать материальными точками.
3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона
4. Учитывая, что длина пружины во время движения не меняется, нить нерастяжима, делаем вывод, что все тела движутся с одинаковым ускорением.
5. Поскольку блок идеальный и нить невесома, силы упругости равны по модулю.
Решение
Расставим силы, действующие на каждое из трёх тел.
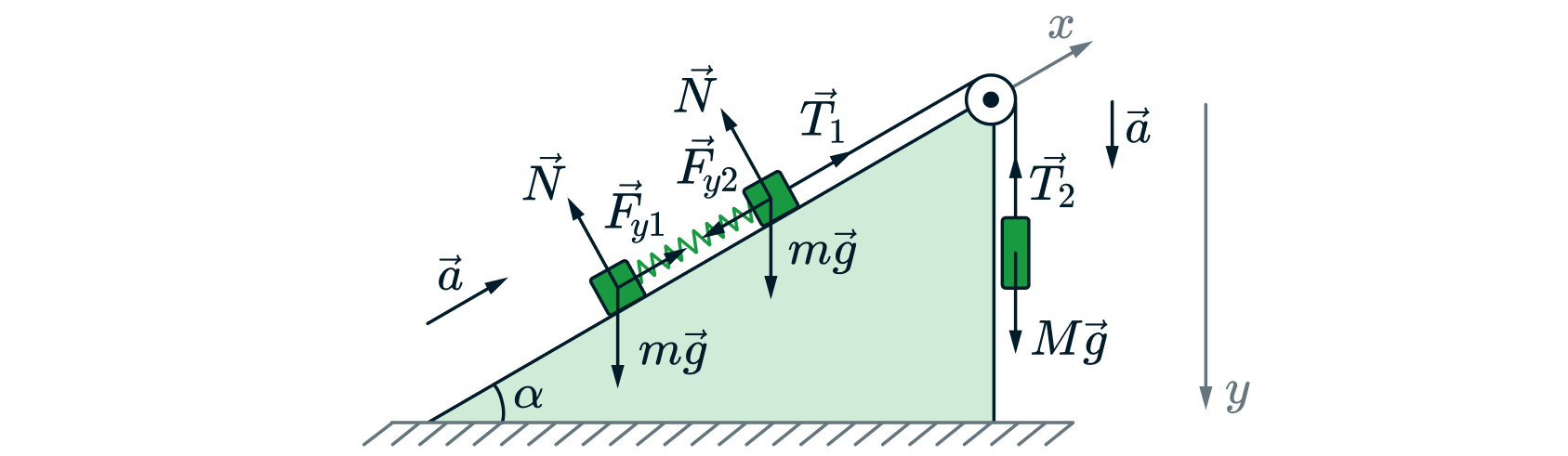
Ускорения всех тел равны. Запишем второй закон Ньютона для каждого из тел:
|
|
При этом из-за невесомости нити и
по третьем закону Ньютона.
Спроецируем третье уравнение на ось , а первые два на ось
|
|
Сложим первые два уравнения
|
|
Тогда
Сила упругости равна
Силу упругости равна:
Тогда
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к грузам модели материальной точки
3. Обосновано применение законов Ньютона для описания движения грузов
4. Обосновано равенство сил натяжения нити и ускорений грузов
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на координатные оси, третий закон Ньютона, закон Гука).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Бруски с массами и
связаны лёгкой нитью, перекинутой через блок, и находятся на наклонной и горизонтальной
поверхностях призмы (см. рисунок). Угол наклона к горизонту одной из поверхностей призмы равен
(
).
Коэффициент трения скольжения бруска о горизонтальную поверхность
, а о наклонную поверхность –
. При
перемещении призмы с некоторым минимальным горизонтальным ускорением a брусок с массой
начинает скользить по призме
влево при натянутой нити. Найти отношение
, где
– ускорение свободного падения. Трением в оси блока пренебречь. Какие
законы Вы используете для решения задачи? Обоснуйте их применение.
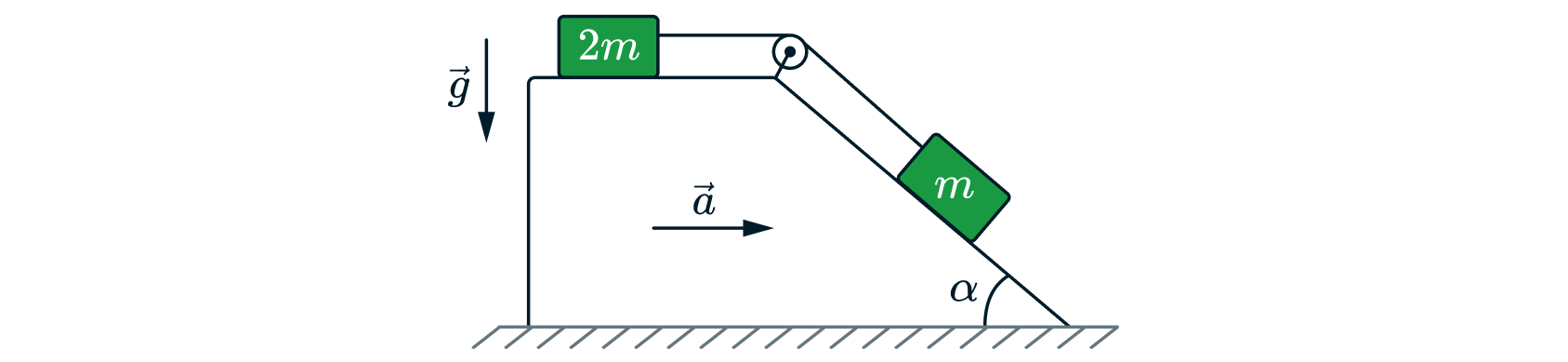
Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Все тела движутся поступательно, поэтому их можно считать материальными точками.
3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Так как нить нерастяжимая, то тела движутся с одинаковыми ускорениями равными .
5. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити
остается неизменной и равной .
Решение
Расставим силы, действующие на бруски

Здесь и
– силы трения,
и
– силы реакции опоры,
и
– силы натяжения нити.
Запишем второй закон Ньютона для груза :
Спроецируем его на оси и
:
|
|
где .
Тогда
Аналогично второй закон Ньютона для вторго груза:
В проекции на оси и
:
|
|
где .
Так как нить невесома, то . Тогда
Сложим (1) и (2)
Тогда
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тел
4. Обосновано равенство сил натяжения нитей, ускорений с которыми движутся тела
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на координатную ось).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
С какой максимальной скоростью можно кататься на велосипеде по поверхности холма, имеющего форму полусферы радиусом 48 м,
оставаясь все время на высоте 38,4 м (отсчитанной от центра кривизны). Коэффициент трения колес о землю 0,8. м/с
Какие законы Вы используете для решения задачи? Обоснуйте их применение.
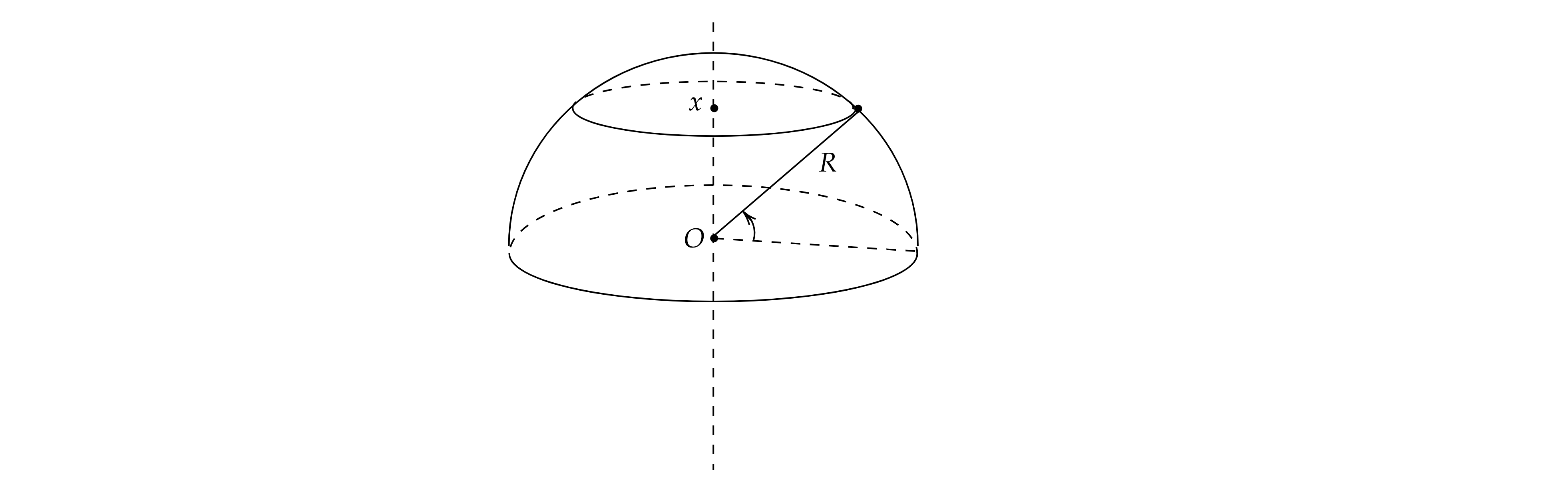
Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО), связанную с Землей.
2. Тело движется поступательно, поэтому его можно считать материальной точкой.
3. Так как тело является материальной точкой, то описывать его движение в ИСО будем, используя законы Ньютона.
4. Так как тело движется по окружности, то оно обладает центростремительным ускорением, направленным к центру окружности, по которой движется тело.
Решение
Так как скорость постоянна, то тангенциальное ускорение равно нулю.
Сделаем рисунок с изображением всех сил.

Запишем второй закон Ньютона:
где – нормальная сила реакции опоры,
– сила трения,
– сила тяжести,
– масса велосипедиста,
–
центростремительное ускорение.
Сила трения равна
где – коэффициент трения.
Центростремительное ускорение равно:
где – скорость велосипедиста.
Спроецируем второй закон Ньютона на оси и
|
|
Отсюда
Найдем тригонометрические значения угла
Также найдем
Тогда
Ошибка.
Попробуйте повторить позже
Вес тела на экваторе составляет от веса этого же тела на полюсе. Найти период вращения планеты вокруг своей оси Т,
если плотность вещества планеты
кг/м
, гравитационная постоянная
. Планету считать
однородным шаром
Пусть – масса тела. Силы, действующие на тело на полюсе и на экваторе, изображены на рисунке, где
и
– силы
тяжести,
и
– силы реакции опор, на которых покоится тело. Поскольку планета представляет собой однородный
шар, силы
и
различаются только направлением, а модули их совпадают:
. Для тела,
покоящегося на полюсе, сила тяжести и сила реакции опоры уравновешены, и его вес по второму закону Ньютона равен
. Тело, находящееся на экваторе, движется по окружности, радиус которой равен радиусу планеты .
Следовательно, сила тяжести и сила реакции опоры не уравновешены, и по второму закону Ньютона для тела на
экваторе:
Здесь – ускорение тела.
Ускорение равно центростремительному и равно:
где – угловая скорость вращения планеты.
Тогда второй закон Ньютона в проекции на ось, направленную в центр планеты, выглядит следующим образом
Поэтому вес тела на экваторе по величине равен
По условию
откуда
Ускорение свободного падения можно выразить из силы гравитации:
где – масса планеты. Отсюда следует, что
Учитывая, что период вращения планеты
Получаем ответ
Ошибка.
Попробуйте повторить позже
Три звезды массы каждая, удалённые от других небесных тел, сохраняют в своем движении конфигурацию
равностороннего треугольника со стороной
. Найдите период
обращения любой зв`езды вокруг центра масс
системы.
Центр масс будет лежат в центре треугольника на пересечении медиан, биссектрис и высот (см. рис. т. ).
Также на рисунке обозначены скорости каждой из звёзд
, они равны, так как звёзды сохраняют конфигурацию
треугольника.
Рассмотрим верхнюю звезду. На неё действует сила притяжения со стороны двух других звезд. При этом силы притяжения равны по
модулю и равны:
Эти силы создают центростремительное ускорение которое равно:
где . При этом высота треугольника равна:
Тогда
Запишем второй закон Ньютона для верхнего тела:
и спроецируем на ось
где . Тогда
Период же равен
Ошибка.
Попробуйте повторить позже
Клин массой находится на шероховатой горизонтальной поверхности стола. Через блок, укреплённый на вершине клина,
перекинута лёгкая нерастяжимая нить, связывающая грузы, массы которых
и
(см. рис). Грузы удерживают,
затем отпускают. После этого грузы движутся, а клин покоится. Гладкая наклонная поверхность клина образует с
горизонтальной плоскостью угол
. Считайте
,
,
. Массой блока и трением в его оси
пренебречь.
1) Найдите ускорение грузов.
2) Найдите силу натяжения нити.
3) Найдите силу нормальной реакции, действующей на клин со стороны стола.
(«Физтех», 2017, 10)

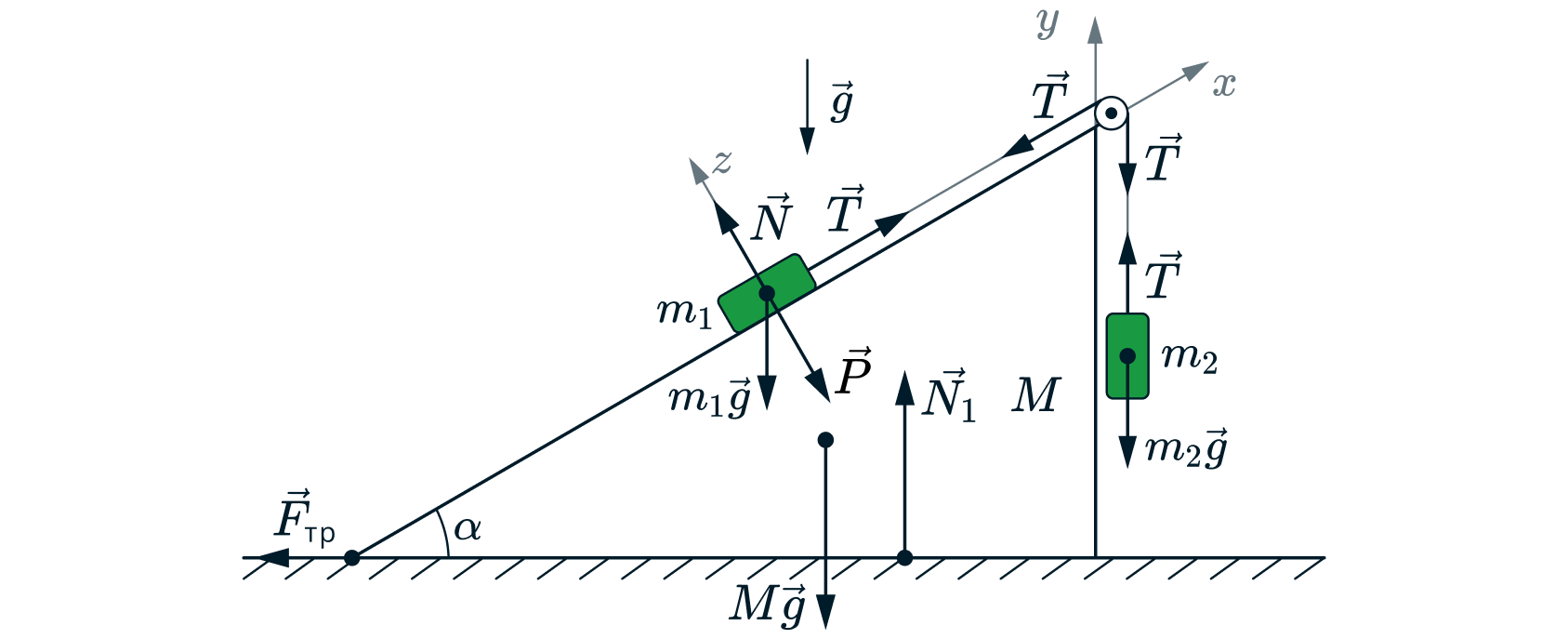
1) Второй закон Ньютона для каждого из грузов запишется в виде:
Пусть левый груз движется вверх, а правый вниз. Тогда второй закон Ньютона в проекциях на ось для левого груза и ось
для правого:
|
|
2) Из второго уравнения системы
3) Запишем второй закон Ньютона для клина:
где – искомая реакция,
– ускорение клина,
- по 3 закону Ньютона.
В проекции на вертикальную ось
можно найти из проекции второго закона Ньютона на ось
для первого груза:
Тогда
Ошибка.
Попробуйте повторить позже
Ящик с шайбой удерживают в покое на наклонной плоскости с углом наклона к горизонту =
(см. рисунок).
Ящик и шайбу одновременно отпускают, и ящик начинает скользить по наклонной плоскости, а шайба — по дну
ящика. Через время
= 1 с шайба ударяется о нижнюю стенку ящика. Коэффициент трения скольжения между
шайбой и ящиком
= 0,23, а между ящиком и наклонной плоскостью
= 0,27. Масса ящика вдвое больше массы
шайбы.
1) Определить ускорение шайбы относительно наклонной плоскости при скольжении шайбы по ящику.
2) На каком расстоянии от нижней стенки ящика находилась шайба до начала движения?
(МФТИ, 2001 )


1) Запишем второй закон Ньютона для бруска:
где – сила трения,
– сила реакции опоры,
– ускорение бруска.
Силу реакции опоры найдем из проекции второго закона Ньютона на ось, перпендикулярную оси движения :
Сила трения же равна:
Спроецируем второй закон Ньютона на ось, совпадающую с осью движения :
Или
2) Запишем второй закон Ньютона для ящика
где – сила реакции опоры клина,
– ускорение ящика,
,
- по 3 закону Ньютона.
Спроецируем на ось :
Сила трения же равна:
Спроецируем второй закон Ньютона на ось :
Найдем ускорение бруска относительно ящика
Тогда длина пути
Ошибка.
Попробуйте повторить позже
На внутренней поверхности прямого кругового конуса в точке А находится маленькая шайба (рис. 1). Конус вращается вокруг его
вертикальной оси . Какова максимальная угловая скорость вращения
, при которой шайба будет неподвижна относительно
конуса? Коэффициент трения шайбы о конус
. Угол между осью конуса
и его образующей
.
см.
Ускорение свободного падения
м/с
Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Тело движется поступательно, поэтому его можно считать материальной точкой.
3. Так как груз является материальной точкой, то описывать его движение в ИСО будем, используя законы Ньютона.
4. Так как тело движется по окружности, то оно обладает центростремительным ускорением, направленным к центру окржности, по которой движется тело.
Решение
На шайбу действует сила тяжести , сила реакции опоры
и сила трения
. Запишем второй закон Ньютона для
шайбы:
где – ускорение шайбы.
Угловая скорость конуса должна совпадать с угловой скоростью шайбы в лабораторной системе отсчета, значит, нормальное
ускорение шайбы равно:
Шайба может соскальзывать как внутрь конуса, так и наружу. Рассмотрим первый случай. Расставим силы, действующие на шайбу в этом случае
Спроецируем второй закон Ньютона на оси и
:
|
|
Отсюда
|
|
Так как тело покоится то величина силы трения не должна превышать . Тогда
Отсюда
с учётом, что
Так как , то частота получается отрицательной, значит, нам подходят все частоты (ограничений снизу нет). Также это
можно было заметить, зная условие не соскальзывания бруска:
Рассмотрим второй случай, шайба выскальзывает наружу. Расставим силы, действующие на шайбу в этом случае
Спроецируем второй закон Ньютона на оси и
:
|
|
Отсюда
|
|
Так как тело покоится то величина силы трения не должна превышать . Тогда
Отсюда
с учётом, что
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Сказано, что тело обладает центростремительным ускорением
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на координатную ось, формула центростремительного ускорения, формула силы трения
скольжения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
На длинную доску массой , скользящую по гладкой горизонтальной поверхности стола со скоростью
, кладут с нулевой
скоростью относительно стола шайбу массы
(см. рисунок). Какое расстояние пройдёт шайба по доске к моменту, когда её
скорость относительно доски станет равной нулю? Коэффициент трения между шайбой и доской равен
. Обоснуйте применимость
законов, используемых для решения задачи.

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Все тела движутся поступательно их движение будем описывать при помощи второго закона Ньютона.
3. Поскольку действующие силы на тела постоянны, то ускорения тел постоянны, значит, движение тел будем описывать при помощи формул равноускоренного движения.
4. Система является замкнутой, значит, для нее применим закон сохранения импульса для описания движения тел.
Решение
Расставим силы и введем оси, как показано на рисунке
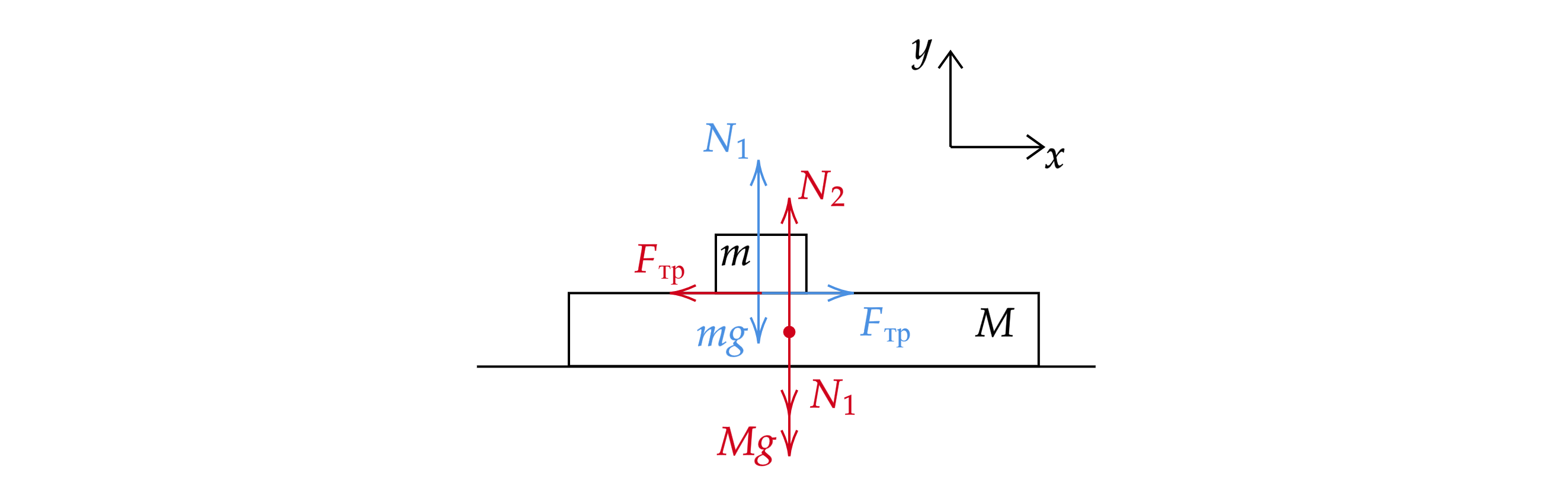
Где – сила реакции опоры со стороны доски (давление шайбы),
– сила реакции опоры со стороны стола,
– сила
трения между поверхностями.
Красным обозначены силы, действующие на доску, синим – на брусок.
Запишем второй закон Ньютона для шайбы:
где – ускорение шайбы.
Аналогично для доски:
где – ускорение доски.
Сила трения скольжения же равна:
где – коэффициент трения между поверхностями.
Для нахождения силы трения скольжения спроецируем второй закон Ньютона для бруска на ось :
тогда сила трения
Спроецируем второй закон Ньютона для шайбы на ось
тогда
Спроецируем второй закон Ньютона для доски на ось :
Скорость шайбы относительно доски становится равной нулю в момент равенства их скоростей. Пусть эта скорость равна .
Запишем закон сохранения импульса для системы шайба+доска
Спроецируем на ось :
Найдём путь, пройденный шайбой, относительно стола по формуле:
где – конечная скорость шайбы,
– начальная скорость шайбы.
Тогда
При этом перемещение направлено вправо (так как начальная скорость равна нулю, а ускорение направлено вправо) Найдём также путь, пройденный доской
где – конечная скорость доски,
– начальная скорость шайбы.
При этом проекция ускорения доски , так как ускорение направлено влево. Тогда
При этом перемещение направлено вправо (так как скорость направлена вправо). Расстояние, пройденное по доске равно:
Ошибка.
Попробуйте повторить позже
Масса Марса составляет 0,1 от массы Земли, диаметр Марса вдвое меньше, чем диаметр Земли. Каково отношение
периодов обращения искусственных спутников Марса и Земли , движущихся по круговым орбитам на небольшой
высоте?
Ускорение спутника, движущегося со скоростью вокруг планеты массой
по круговой траектории радиуса
, равно
,
т. е. Период обращения спутника
Критерии проверки
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное правильное решение, включающее следующие элементы:
1) верно записаны формулы, выражающие физические законы, применение которых необходимо для
решения задачи выбранным способом (в данном решении — закон всемирного тяготения, второй закон
Ньютона и формула расчета центростремительного ускорения);
2) проведены необходимые математические преобразования и расчеты, приводящие к правильному
числовому ответу, и представлен ответ. При этом допускается решение "по частям"(с промежуточными
вычислениями).
2 балла ставится если:
_________________________________________________________________________________________________________________
Приведено решение, содержащее ОДИН из следующих недостатков:
— в необходимых математических преобразованиях и (или) вычислениях допущены ошибки;
— представлено правильное решение только в общем виде, без какихлибо числовых расчетов;
— правильно записаны необходимые формулы, записан правильный ответ, но не представлены
преобразования, приводящие к ответу.
1 балл ставится если:
_________________________________________________________________________________________________________________
Приведено решение, соответствующее ОДНОМУ из следующих случаев:
— в решении содержится ошибка в необходимых математических преобразованиях, и отсутствуют
какие-либо числовые расчеты;
— записаны и использованы не все исходные формулы, необходимые для решения задачи, или в ОДНОЙ
из них допущена ошибка.
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла.
Ошибка.
Попробуйте повторить позже
На гладкий клин, расположенный на гладком столе, положили шайбу массой кг и начали действовать на неё с
горизонтальной силой
Н (см. рисунок). Клин упирается в гладкую стенку. Найдите силу, с которой клин давит на боковую
стенку при движении шайбы вверх, если угол наклона клина равен
. Сделайте рисунок с указанием сил, действующих на
шайбу и клин, укажите искомую силу давления на боковую стенку. Какие законы Вы использовали для описания движения?
Обоснуйте их применение к данному случаю.
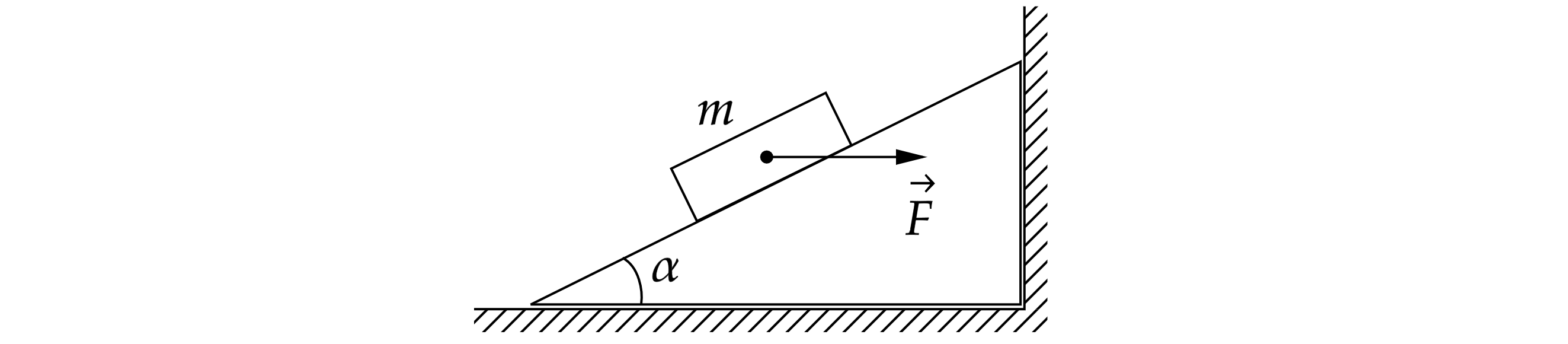
На шайбу действует сила тяжести , сила
и сила нормальной реакции опоры со стороны клина
. Введём оси
и
.
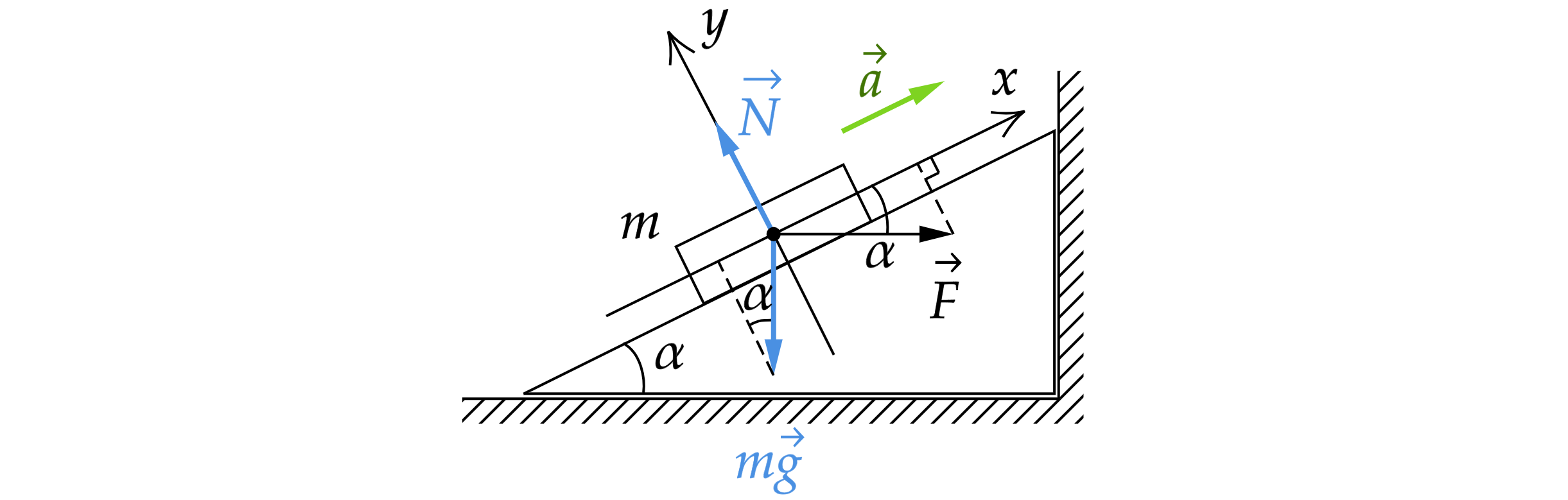
Запишем второй закон Ньютона
Проецируем на оси и
Рассмотрим клин и силы, действующие на него (обозначены красным). Шайба на клин действует с силой , при этом по
третьему закону Ньютона
, сила тяжести
, сила нормальной реакции опоры со стороны стола
и сила нормальной
реакции опоры со стороны стенки
. При этом по третьему закону Ньютона сила давления клина на стенку
равна по
модулю
.
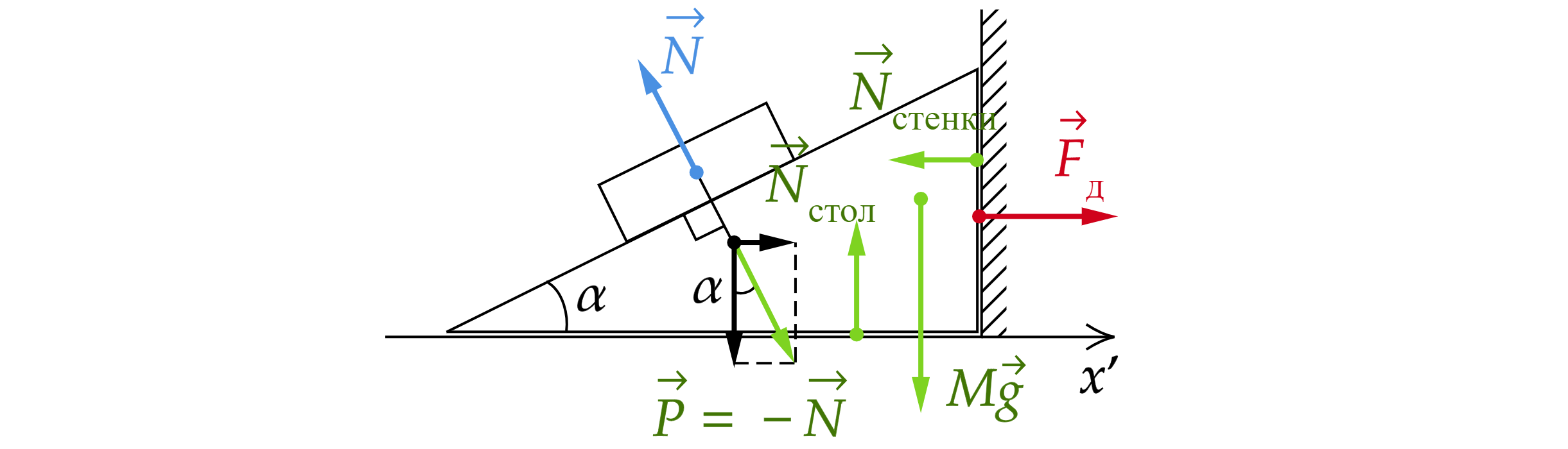
Так как клин неподвижен, то сумма сил, действующих на клин равна нулю. Рассмотрим ось
Отсюда
Ошибка.
Попробуйте повторить позже
По гладкой горизонтальной поверхности стола движется клин массой M. По шероховатой наклонной поверхности клина равномерно
(относительно клина) вниз движется брусок массой m (см. рисунок). Угол наклона клина , а коэффициент трения бруска о клин
равен
. С какой горизонтальной силой
, действуют на клин. Какие физические законы Вы использовали при решении задачи?
Обоснуйте их применение в данном случае. Сделайте рисунок с указанием сил, действующих на брусок и клин.

Обоснование
Изобразим силы, действующие на брусок:

Систему отсчета, связанную с Землей, будем считать инерциальной. Движение бруска поступательное. Следовательно, его можно
считать материальной точкой.
При движении бруска по плоскости клина на него действуют силы тяжести, трения и реакции опоры. На клин действуют сила
тяжести, сила трения между бруском и клином, сила реакции опоры, вес бруска и приложенная горизонтальная сила. Движение
клина по горизонтальной поверхности поступательное. Следовательно, его можно описывать моделью материальной
точки.
Так как брусок относительно клина движется равномерно, то клин и брусок относительно Земли движутся с одинаковым
ускорением. В ИСО для обоих тел выполняется второй закон Ньютона.
Решение
Силы трения между бруском и клином – парные, по третьему закону Ньютона эти силы равны по модулю в ИСО . Вес
бруска по третьему закону Ньютона равен силе реакции опоры
.
Запишем второй закон Ньютона для бруска в проекциях на координатные оси и
:
Сила трения скольжения: . Отсюда
Поделим первое уравнение на второе
Тогда
Запишем второй закон Ньютона для системы "клин+брусок":
Спроецируем на ось :
Тогда силу, действующую на клин, можно найти подставив ускорение в формулу:
Ошибка.
Попробуйте повторить позже
Призма находится на горизонтальной поверхности шероховатого стола (см. рисунок). На поверхность призмы, наклонённую под
углом к горизонту, положили брусок массой
кг и отпустили. Он стал соскальзывать, а призма осталась в покое.
Коэффициент трения скольжения между бруском и призмой равен
. Найти силу трения между призмой
и столом. Какие физические законы Вы использовали при решении задачи? Обоснуйте их применение в данном
случае.

Изобразим силы, действующие на призму и брусок. На брусок действует сила тяжести , нормальная сила реакции опоры
,
– сила трения со стороны призмы. На призму действует сила тяжести
, нормальная сила реакции
опоры со стороны стола
, вес бруска
, сила трения со стороны бруска
, сила трения со стороны стола
.
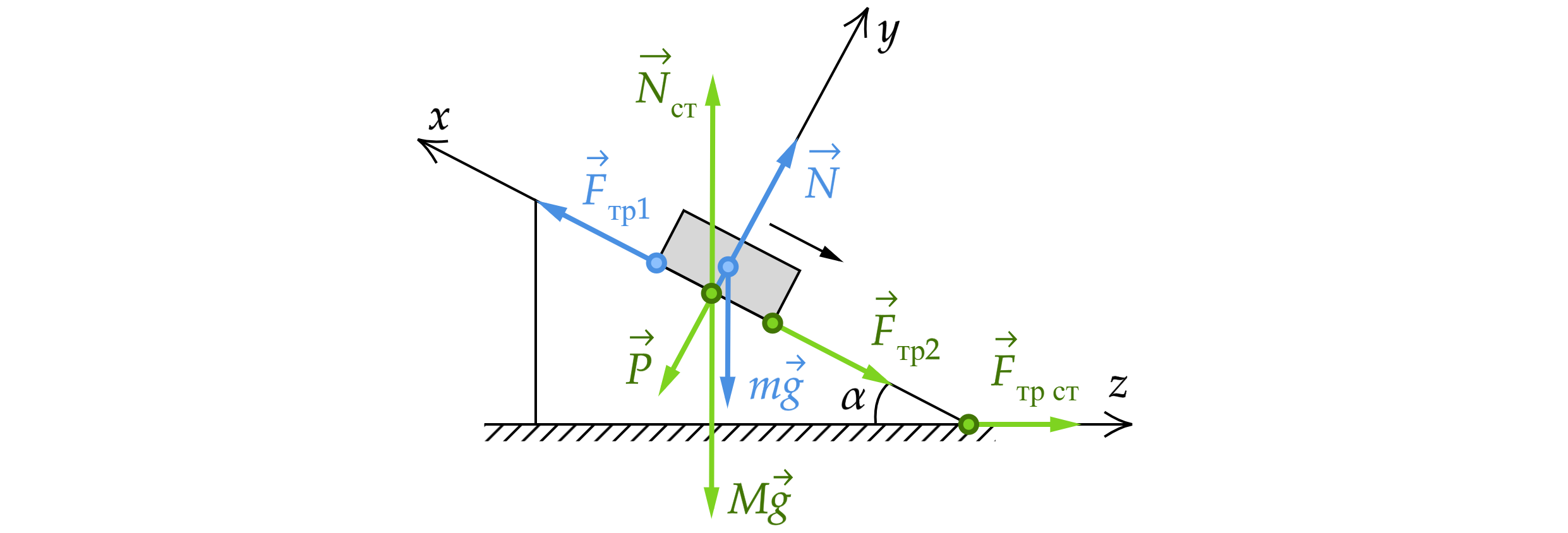
При этом, по третьему закону Ньютона ,
.
Запишем второй закон Ньютона для бруска
где – ускорение бруска.
Спроецируем на ось :
Сила трения же равна
Запишем второй закон Ньютона для призмы
где – масса призмы,
– ускорение призмы.
Так как призма покоится, то . Спроецируем второй закон Ньютона на ось
:
с учётом предыдущих уравнений
Ошибка.
Попробуйте повторить позже
На наклонной плоскости с углом при основании находится брусок массой
кг, связанный невесомой нерастяжимой
нитью, перекинутой через невесомый блок (трение в оси блока отсутствует), с грузом массой
кг (см. рисунок), При
каком коэффициенте трения
бруска о плоскость груз будет опускаться с ускорением
м/с
? Сделайте
рисунок с указанием сил, действующих на брусок и груз. Обоснуйте применимость законов, используемых для решения
задачи.

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Все тела движутся поступательно, поэтому их можно считать материальными точками.
3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Учитывая, что нить нерастяжима, блок идеальный, делаем вывод, что все тела движутся с одинаковым ускорением
5. Учитывая, что нить невесома, блок идеальный, делаем вывод, что силы натяжения, приложенные к телам, равны по модулю.
Решение
Введем оси, как показано на рисунке
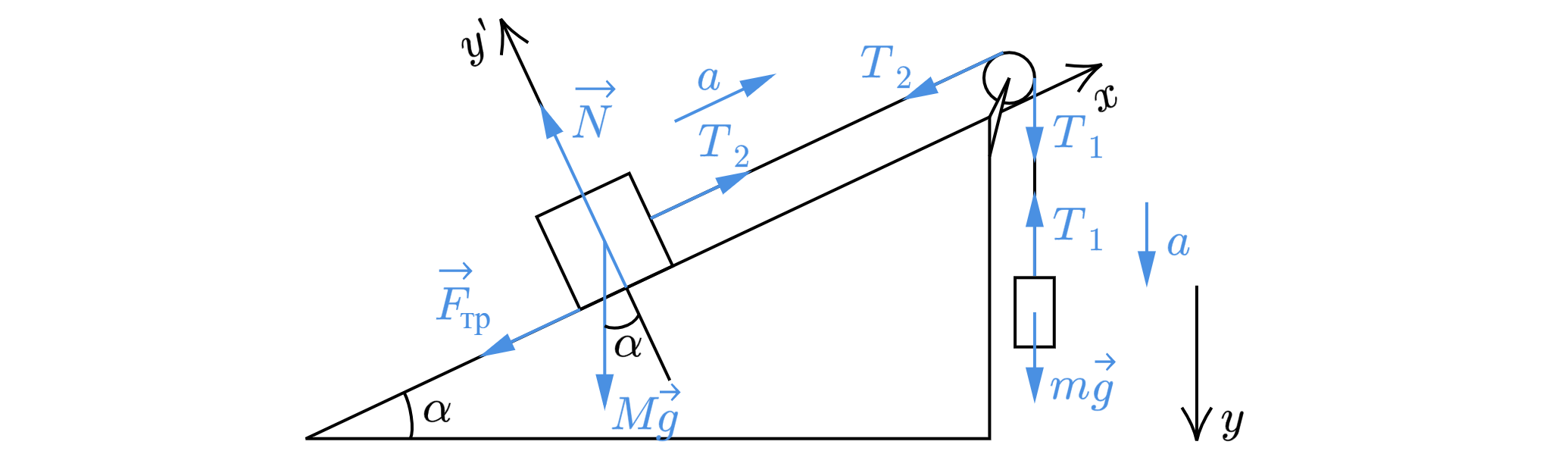
Запишем второй закон Ньютона для тела массой
где – сила натяжения нити,
– сила трения,
– сила реакции опоры,
– ускорение тела.
Запишем второй закон Ньютона для тела массой
где – сила натяжения нити,
– ускорение тела.
Спроецируем второй закон Ньютона на введенные оси для каждого из тел
|
|
Так как нить невесомая, то , при этом ускорения тел равны
из-за нерастяжимости нити, а сила трения
равна
. Из (3)
Из (2)
Объединим (1), (4) и (5)
Отсюда
Ошибка.
Попробуйте повторить позже
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами и
связанные нерастяжимой невесомой нитью длиной
Нить закрепили на оси так, что грузы располагаются по разные
стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). При вращении штанги с
частотой 900 об/мин модуль силы натяжения нити, соединяющей грузы,
Определите длину нити
Какие законы Вы
используете для решения задачи? Обоснуйте их применение.

Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Размеры грузов малы по сравнению с размерами штанги, поэтому будем описывать грузы моделью материальной точки.
3. При вращении тела будут двигаться по окружности, из пункта 1 описывать их движение будем вторым законом Ньютона, при этом ускорение тел будет центростремительное.
4. Так как по условию нить легкая, то силы натяжения нити будут одининаковы для обоих грузов.
5. Так как грузы находятся на одном стержне, то полный оборот они совершают за одно и то же время, т.е. периоды их
обращения равны. Период можно рассчитать по формуле , так как периоды равны, то равны и угловые скорости
вращения. Период и частота связаны соотношением
, а так как периоды равны то и частоты тоже будут
равны.
Решение
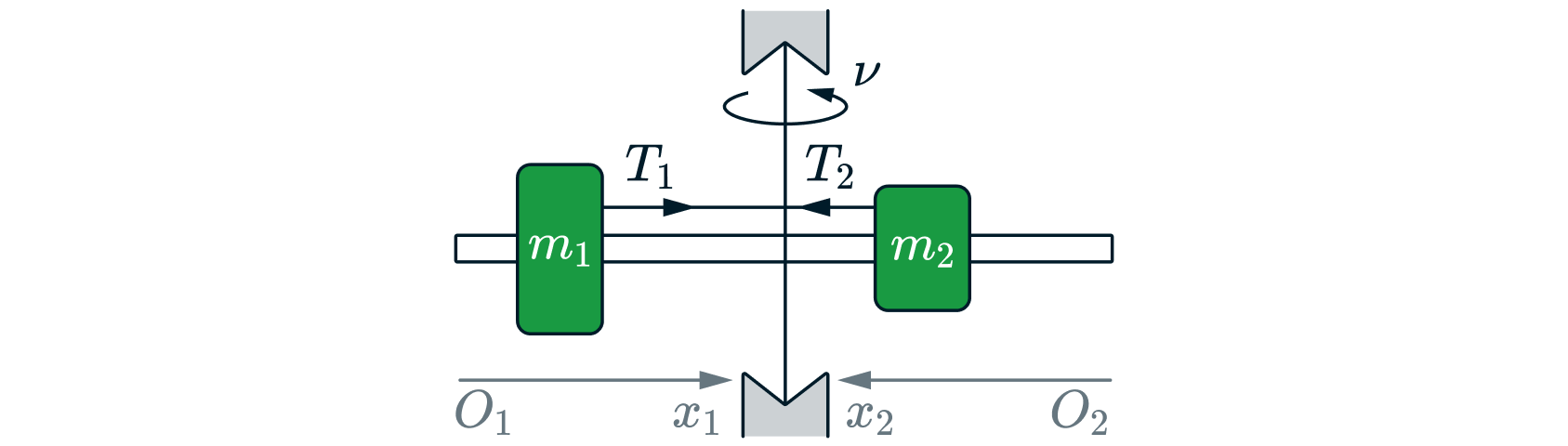
Для каждого груза выберем инерциальную систему отсчёта, ось которой направлена вдоль штанги к оси вращения (см. рисунок), и запишем в проекциях второй закон Ньютона для грузов:
|
|
где ,
– центростремительные ускорения грузов,
– циклическая частота,
– радиус
обращения.
Так как , а
, то найдем радиус обращения первого груза из системы уравнений и силу натяжения
нити.
Отсюда длина нити
Ошибка.
Попробуйте повторить позже
Под действием постоянной горизонтальной силы клин массой
движется по гладкой горизонтальной поверхности
стола. По шероховатой поверхности клина, составляющей угол
с горизонтом (относительно клина), равномерно скользит
вниз брусок массой
. Коэффициент трения между бруском и клином
. Найдите модуль ускорения клина.
Сопротивлением воздуха пренебречь. Сделайте рисунок с указанием сил, действующих на брусок. Обоснуйте применимость законов,
используемых для решения задачи.

Источники:
Обоснование
Изобразим силы, действующие на брусок:
.png)
Систему отсчета, связанную с Землей, будем считать инерциальной. Движение бруска поступательное. Следовательно, его можно
считать материальной точкой.
При движении бруска по плоскости клина на него действуют силы тяжести , трения скольжения
и реакция опоры
. На клин действуют сила тяжести
, сила трения между бруском и клином
, сила реакции опоры
, вес бруска
и
приложенная горизонтальная сила
. Движение клина по горизонтальной поверхности поступательное. Следовательно, его можно
описать моделью материальной точки.
Так как брусок относительно клина движется равномерно, то клин и брусок относительно Земли движутся с одинаковым
ускорением . В ИСО для обоих тел выполняется второй закон Ньютона.
Силы трения между бруском и клином — парные, по третьему закону Ньютона эти силы равны по модулю в ИСО. Вес бруска по
третьему закону Ньютона равен силе реакции опоры .
Решение
Запишем второй закон Ньютона для бруска:
Выберем оси: направим горизонтально вправо,
направим вертикально вверх. В проекциях на координатные
оси:
Сила трения между бруском и поверхностью клина:
Решая данную систему, находим ускорение бруска:
Подставляя числовые значения, находим ускорение бруска (равное ускорению клина):
Ответ: .
Ошибка.
Попробуйте повторить позже
На горизонтальном столе находится доска массой и длиной
, на левый край которой помещен небольшой
брусок массой
Брусок и доска соединены через идеальный блок легкой и нерастяжимой нитью. Коэффициент трения
между доской и бруском
, а поверхность стола гладкая. Чему равна сила
, если брусок соскальзывает с края доски
спустя
после начала движения. Сделайте рисунок с указанием сил, действующих на доску и брусок. Обоснуйте
применимость законов, используемых для решения задачи.
.png)
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Поскольку тела связаны нерастяжимой нитью их ускорения равны.
3. Поскольку тела связаны легкой нитью, блок идеальный и трение отсутствует, модули сил натяжения нитей, действующих на тела равны.
4. Поступательное движение тел в ИСО будем описывтаь при помощи законов Ньютона.
Рассмотрим задачу с точки зрения динамики:
Бруски движутся под действием сил, которые изображены на рисунке
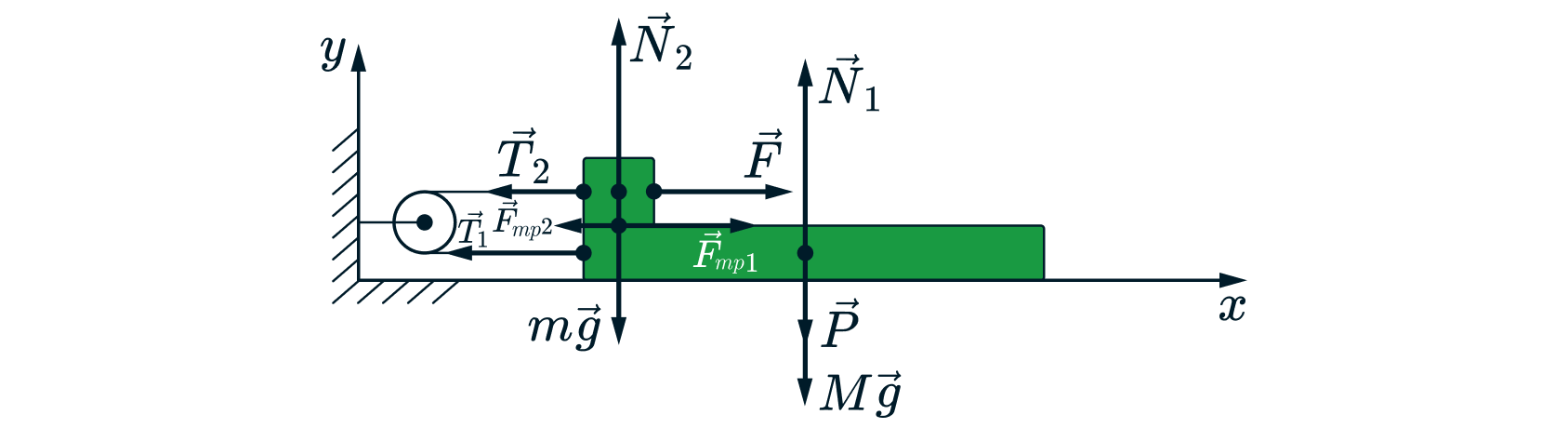
где и
– модули силы натяжения нити,
и
– модули силы трения,
и
– сила тяжести,
– сила
реакции опоры стола,
– сила реакции доски,
– вес бруска.
Запишем второй закон Ньютона для бруска и доски
Так как нить нерастяжимая, то . По третьему закону Ньютона
,
и
.
Спроецируем (1) на оси
и
|
|
Аналогично для (2)
|
|
Сила трения же равна
Тогда
|
|
Сложим два уравнения
Теперь применим кинематический подход:
Брусок двигается относительно доски равноускоренно и прямолинейно, тогда его движение описывается законом:
где – момент времени,
– координата бруска в момент времени
,
– скорость бруска в начальный момент времени,
–
ускорение бруска относительно доски (
).
В момент времени уравнение приобретёт вид:
Подставим формулу для ускорения в формулу для силы:
|
|



