Раскраски
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дана клетчатая доска Фигура принц умеет ходить по горизонтали и вертикали, делая ходы сначала на 1 клетку, потом — на две (в
одном направлении), потом опять на одну и т.д. Может ли принц, встав на некоторую клетку, обойти все остальные клетки доски, побывав
на каждой ровно по одному разу?
Источники:
Подсказка 1
Попробуем представить некоторые варианты передвижения принца за несколько ходов. Например, как можно обобщить его передвижения за ход вида "2 клетки" от клетки, на которой он был до этого хода?
Подсказка 2
Заметим, что, если мы условно разделим поле на области размера 2х2, то каждый ход вида "2 клетки" принц выходит из одной области и входит в другую. Тогда пусть эти области покрашены в два чередующихся цвета, так, что соседние области имеют разные цвета. Что нам это может дать?
Подсказка 3
Получаем, что на чётных ходах принц будет менять цвет клетки, на которой стоит. Тогда можно условно сопоставить клетки разных цветов по ходам: после второго хода и после первого — разные цвета, после четвертого хода и третьего — разные цвета... и так далее. Тогда как можно оценить количество клеток каждого цвета?
Подсказка 4
То есть свободные варианты для цветов (когда нельзя ходы принца разбить на пары, дающие равное количество обоих цветов) — это только первый и последний ход, что дает максимальное различие в количестве клеток каждого цвета, равное двум. А теперь посмотрим, сколько у нас действительно клеток каждого цвета по нашей раскраске, и сравним результаты.
Предположим, что такое возможно. Покрасим клетки доски как на рис.
Заметим, что при втором, четвертом, …, -м ходе принц меняет цвет клетки. Значит, количество клеток цветов
и
может
отличаться не более чем на
поскольку все клетки, начиная со второй и заканчивая
-й, бьются на пары вторая-третья,
четвертая-пятая, …, тридцать четвертая-тридцать пятая, и внутри каждой пары клетки имеют разный цвет. Ну а первая и последняя клетки
могут иметь любой цвет.
Таким образом, количество клеток цветов и
отличается не более чем на
Но с другой стороны, клеток цвета
больше на
—
противоречие.
Нет, не может
Ошибка.
Попробуйте повторить позже
Петя красит каждую клетку доски в чёрный или белый цвет так, чтобы клетки каждого цвета образовывали многоугольник. Затем
Вася разрезает доску на двухклеточные доминошки. Петя стремится к тому, чтобы в итоге получилось как можно больше разноцветных
доминошек, а Вася — к тому, чтобы их получилось как можно меньше. Наличие какого наибольшего числа разноцветных доминошек
может гарантировать Петя, как бы ни действовал Вася? (Напомним, что граница многоугольника — замкнутая ломаная без
самопересечений.)
Источники:
Подсказка 1
Давайте для начала считать, что у нас дан прямоугольник 2n×2m, где m и n - натуральные числа. Нас просят найти оценку на количество разноцветных доминошек (прямоугольник 2×1). Давайте попробуем составить пример, чтобы понимать, какую примерно оценку нам хочется получить.
Подсказка 2
Назовем каёмкой множество всех клеток прямоугольника, прилегающих к границе. Что будет, если "углы" (2 подмножества клеток каёмки, образующие углы 90°) покрасить в белый и черный (то есть, будут две разноцветных "галочки")? А какая конструкция многоугольника тут может быть выигрышной?
Подсказка 3
Попробуйте в прямоугольнике без клеток каёмки красить так, чтобы у нас получались "плюсы" (многоугольник из 5 клеток одного цвета, имеющий одну центральную клетку, к ребрам которой присоединены все остальные). Может ли у нас из такой конфигурации получиться оценка?
Подсказка 4
Давайте также изначально раскрасим клетки в шахматном порядке в красный и синий цвета так, чтобы левая нижняя клетка была красной.
Подсказка 5
Наш прямоугольник будет выглядеть следующим образом: занумеруем строки снизу-вверх, столбцы - слева-направо. Покрасим в черный все клетки первого столбца, в остальных столбцах с номерами, дающими остаток 1 от деления на 4, — все клетки, кроме самой верхней, во всех столбцах с чётными номерами, кроме самого правого, — все синие клетки, во всех остальных столбцах — только самую нижнюю клетку. Будет получаться не менее 1 + (m - 1)(n - 1) разноцветных доминошек. Попробуем доказать эту оценку.
Подсказка 6
Исходя из раскраски в красный и синий цвета, что мы можем сказать про, например, черный многоугольник, который будет получать Петя?
Подсказка 7
Попробуйте доказать, что в каждом черном многоугольнике должно быть хотя бы на 1 + (m - 1)(n - 1) больше синих клеток, чем красных.
Подсказка 8
Оцените количество доминошек, в которых будет одна синяя клетка черного многоугольника, но не будет красной клетки черного многоугольника.
Подсказка 9
У нас получится, что при разрезании будет хотя бы 1 + (m - 1)(n - 1) доминошка такого вида, так как в каждой доминошке по одной синей и красной клетке. А что можно сказать про них?
Подсказка 10
Все такие доминошки будут черно-белыми. Убедитесь, что оценка удовлетворяет нашему примеру.
Подсказка 11
Мы доказали, что 1 + (m - 1)(n - 1) - нижняя оценка. Надо теперь проверить, является ли она верхней. Какой факт о клетках вне каёмки нужно доказать?
Подсказка 12
Достаточно доказать, что белые клетки каёмки образуют связное по сторонам множество клеток. Тогда белые клетки каёмки будут представлять собой несколько последовательных клеток. Что нам может дать это утверждение?
Подсказка 13
Докажите, что Вася, разрезав всю каёмку, получит не более одной разноцветной доминошки.
Подсказка 14
Клетки белого многоугольника образуют связное по сторонам множество клеток. Что можно сказать про белые не соседние клетки каёмки и путь γ между ними по белым клеткам, не содержащий другие клетки каёмки?
Подсказка 15
Если он существует, тогда найдется и путь по белым клеткам каёмки. Что можно сказать о частях прямоугольника, на которые путь γ разбивает прямоугольник?
Подсказка 16
Между ними не будет пути, который не содержит клетки γ. Тогда γ разбивает каёмку на две связные части. Могут ли быть в обеих частях каёмки черные клетки? Обоснуйте, что нет, сделайте соответствующие выводы и задача будет решена.
Решим задачу для прямоугольника , где
— произвольные натуральные числа. Мы докажем, что ответом является число
Сначала покажем, что Петя может раскрасить доску так, чтобы при любом разрезании Васи получилось не менее, чем
разноцветных доминошек. Покрасим прямоугольник шахматным образом в синий и красный цвета так, чтобы левая
нижняя клетка была красной. Пете достаточно добиться того, чтобы в чёрном многоугольнике было на
больше синих
клеток, чем красных. Действительно, тогда при любом разрезании на доминошки будет хотя бы
доминошек, в которых
есть синяя клетка чёрного многоугольника, но нет красной (так как в каждой доминошке ровно одна синяя и ровно одна красная клетка),
все такие доминошки будут чёрно-белыми.
Занумеруем строки снизу-вверх, а столбцы слева-направо. Добиться такого перевеса синих клеток в чёрном многоугольнике Петя может,
например, покрасив в точности следующие клетки в чёрный цвет: все клетки первого столбца, в остальных столбцах с
номерами дающими остаток от деления на
— все клетки, кроме самой верхней, во всех столбцах с чётными номерами,
кроме самого правого, — все синие клетки, во всех остальных столбцах — только самую нижнюю клетку (см рисунок).
Действительно, тогда в первом столбце синих и красных клеток одинаковое количество, в остальных столбцах с нечётными
номерами красных клеток на одну больше, чем синих, а в каждом чётном столбце, кроме последнего, синих клеток на
больше, чем красных, в последнем столбце синих на одну больше, чем красных, итого суммарно синих больше, чем
красных, на
клеток. При такой покраске как чёрные, так и белые клетки образуют
многоугольник.
Теперь докажем, что как бы Петя ни раскрасил клетки, Вася сможет добиться того, чтобы разноцветных доминошек было не более, чем
Назовём каёмкой множество всех клеток прямоугольника, прилегающих к границе. Достаточно доказать, что
Вася всегда сможет разбить все клетки, отличные от клеток каёмки, на доминошки так, чтобы среди них было не более
разноцветных, и что он всегда сможет разрезать каёмку на доминошки так, чтобы среди них было не более одной
разноцветной.
Теперь докажем второе утверждение. Для этого достаточно доказать, что белые клетки каёмки образуют связное по сторонам множество клеток. Действительно, тогда в каёмке белые клетки представляют собой несколько последовательных клеток, и Вася может порезать всю каёмку на доминошки, порезав при этом всю белую часть на доминошки, за исключением, возможно, одной клетки (если в каёмке белых клеток нечётное количество). Таким образом, разрезав каёмку, Вася получит не более одной разноцветной доминошки.
Итак, докажем связность множества белых клеток каёмки. Клетки белого многоугольника образуют связное по сторонам множество
клеток, поэтому достаточно доказать, что если между некоторыми двумя различными не соседними белыми клетками в каёмке есть путь
по белым клеткам, не содержащий других клеток каёмки, то между ними есть и путь по белым клеткам каёмки, далее это и докажем.
Клетки пути
разбивают прямоугольник на две (необязательно связные по сторонам) части, между которыми нет путей по клеткам, не
содержащих клеток пути
. Значит,
разбивает каёмку на две связные части, только в одной из которых могут быть чёрные клетки (так
как чёрные клетки сами образуют связное по сторонам множество клеток, не содержащее клеток пути
). Следовательно, одна из
частей каёмки полностью белая, и поэтому между рассмотренными белыми клетками каёмки есть путь по белым клеткам
каёмки.
Ошибка.
Попробуйте повторить позже
В каждой клетке доски лежит по рублёвой монете. Даша и Соня играют, делая ходы по очереди, начинает Даша. За один ход
можно выбрать любую монету и передвинуть её: Даша двигает монету на соседнюю по диагонали клетку, Соня — на соседнюю по стороне.
Если две монеты оказываются в одной клетке, одна из них тут же снимается с доски и достаётся Соне. Соня может остановить игру
в любой момент и забрать все полученные деньги. Какой наибольший выигрыш она может получить, как бы ни играла
Даша?
Источники:
Подсказка 1:
Чтобы придумать стратегию за Соню, попробуйте разбить доску на какие-нибудь маленькие части, в рамках которых она сможет легко получать монеты.
Подсказка 2:
Разбейте на квадраты 2 на 2. Давайте заметим, что если в таком квадрате есть хотя бы 2 монеты, то Соня легко сможет получить одну из них (почему?). Исходя из этого, можно понять, каким будет ответ.
Подсказка 3:
Итак, скорее всего вы поняли, что ответ будет 300. Осталось придумать стратегию за Дашу, с помощью которой она всегда сможет сохранить 100 монет на доске. Попробуйте выбрать 100 монет, находящихся в каких-то определённых столбцах.
Подсказка 4:
Будет здорово, если эти столбцы не будут рядом. Тогда Соне будет сложнее забрать какую-то из выбранных монет. Значит, можно взять, например, нечётные столбцы и придумать стратегию, при которой после каждого хода Даши выбранные монеты находятся в этих столбцах.
Сначала приведём стратегию за Соню. Пока она не получила больше 299 монет, перед её ходом на доске остаётся хотя бы 101 монета.
Разобьем доску на 100 квадратов Получается, что какие-то две монеты лежат в одном и том же квадрате
Если эти две
монеты соседние по стороне, то Соня надвигает одну на другую, и получает ещё одну монету. Если они стоят по диагонали, то Соня сдвигает
одну из них в столбец к другой (здесь и далее столбец имеет длину 2, строка — длину 200). Теперь, какой бы ход ни сделала Даша, эти две
монетки всё ещё будут соседними по стороне (либо одна будет снята и уйдёт в доход Сони), значит, своим следующим ходом Соня
сможет получить ещё одну монетку. Таким образом, Соня всегда сможет увеличивать свой выигрыш, пока он меньше
300.
Теперь покажем, как играть за Дашу, чтобы Соня не получила больше 300 монет. Пронумеруем столбцы числами от 1 до 200 по порядку, выберем в каждом нечётном столбце по одной монетке и мысленно покрасим их в красный цвет. Даше достаточно обеспечить, чтобы красные монетки всегда оставались на доске. Для этого, в свою очередь, достаточно, чтобы две красные монеты никогда не попадали в одну клетку, потому что когда в клетку попадают красная и не красная монеты, можно считать, что с доски снимается не красная.
Назовём расположение монет на доске стабильным, если по одной красной монете лежит в столбцах а
ещё одна располагается в одном из двух последних столбцов 199, 200. Легко видеть, что после любого хода из стабильной
позиции две красные монеты не окажутся в одной клетке. Даша будет играть так, чтобы после каждого её хода получалась
стабильная позиция. Если после хода Сони позиция осталась стабильной, то Даша двигает сотую красную фишку между двумя
последними столбцами, так же Даша поступит и своим первым ходом. Если же после хода Сони позиция перестала быть
стабильной, то Соня подвинула одну из красных монет из некоторого столбца
в соседний столбец. Тогда Даша своим ходом
вернёт её в столбец
Таким образом, на доске всегда останется хотя бы 100 монет, и Соня заработает не более трёхсот
рублей.
300
Ошибка.
Попробуйте повторить позже
Вася и Петя играют в морской бой на доске , правда у них остался только один корабль
и всё, так что правила такие: Вася
выставляет корабль, а Петя отмечает
клеток. Его задача попасть хотя бы в одну клетку корабля. При каком наименьшем
Петя
гарантированно сможет победить?
Оценка. Расставим на доске 21 корабль так, как показано на рисунке. Таким образом, для поражения каждого из кораблей необходимо отметить по крайней мере 21 клетку.
.png)
Пример. Отметим все клетки на диагоналях, параллельных главной, начиная с левой верхней клетки, через клетки, как
показано на рисунке. При этом будет закрашена ровно
клетка, а в любом прямоугольнике
будет хотя бы одна
закрашенная.
.png)
21
Ошибка.
Попробуйте повторить позже
Какое наибольшее количество квадратиков можно поместить, располагая стороны квадратиков по линиям сетки, в
клеточный прямоугольник
если любым двум квадратикам можно иметь либо одну общую клеточку, либо ни
одной?
Источники:
Подсказка 1
Как могут пересекаться квадратики?
Подсказка 2
Могут ли, например, 3 квадрата иметь общую клетку?
Подсказка 3
Нет, иначе бы какие-то два из них пересеклись по 2 клеткам, что противоречит условию.
Подсказка 4
Попробуйте, отталкиваясь от этого, придумать раскраску.
Подсказка 5
Пусть клетки пронумерованы по строкам и столбцам, начиная с 1. Что, если закрасить все клетки, у которых номер строки и номер столбца — четные?
Для любой клетки существует не более чем два квадрата пересекающихся только по этой клеточке, так как если взять хотя бы 3
квадрата, содержащих общую клетку, то какие-то два из них будут пересекаться по двум клеткам.
Закрасим клетки во втором, четвертом, шестом и так далее горизонтальном ряду, например, снизу вверх, причем закрашиваем в каждом
ряду вторую, четвертую, шестую и так далее клеточки, например, слева направо (см. рис.). Закрашенных клеточек получится

Очевидно, что любой квадрат помещенный в данный прямоугольник, содержит ровно одну закрашенную клеточку. На неё может
быть наложено, как было замечено, не более двух квадратов
поэтому всего, по данным правилам, квадратов можно поместить не
более
Пример. Укладываем у стороны длиной вплотную друг к другу слева направо ряд из
квадратов; следующий ряд из
квадратов выкладываем со сдвигом на
клетку вверх и вправо, следующий ряд — со сдвигом вверх и влево, и так далее (см. рис.).
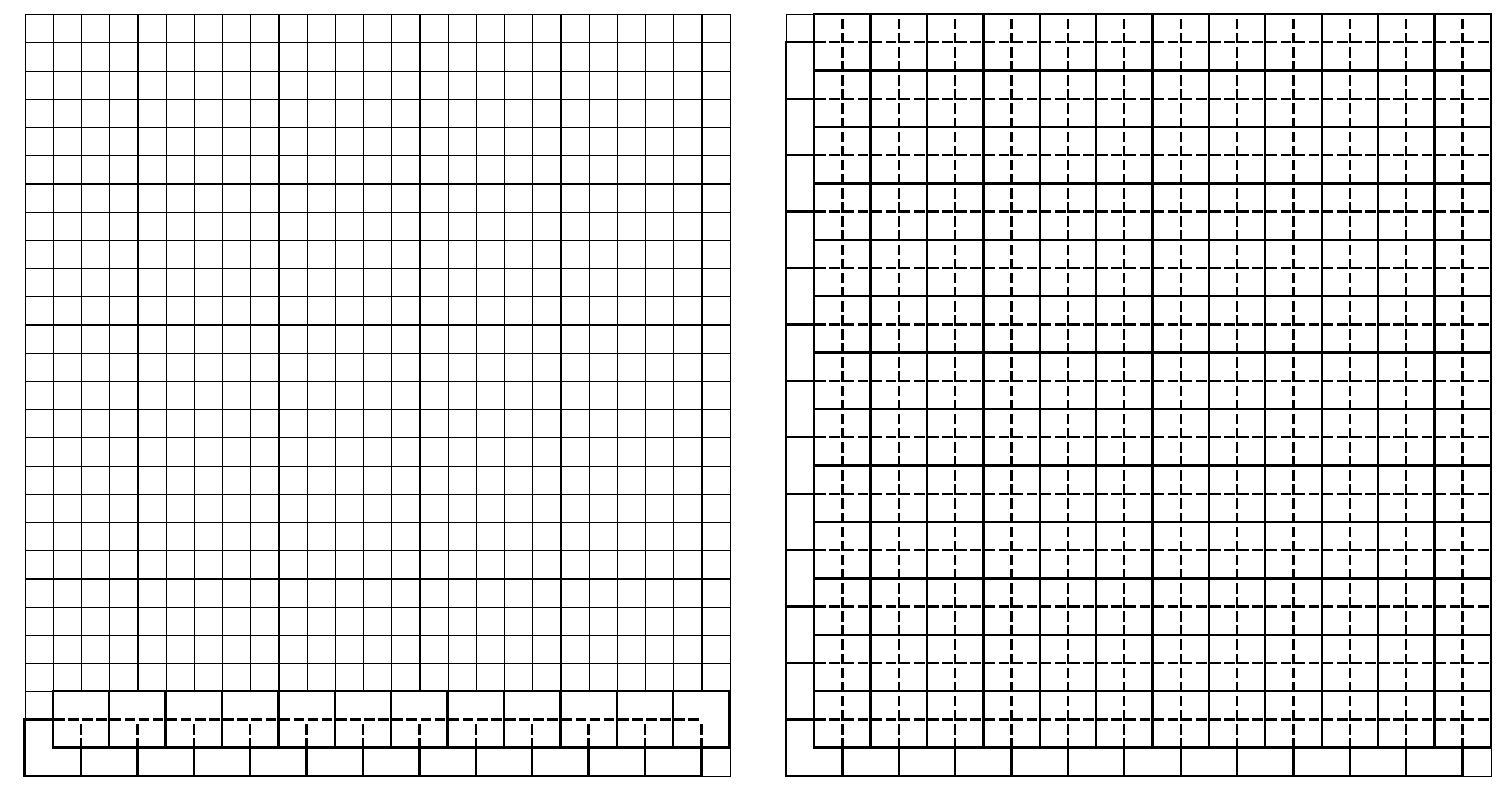
312
Ошибка.
Попробуйте повторить позже
На шахматной доске отметили клеток. Докажите, что можно расставить
не бьющих друг друга ладей так, чтобы не менее
ладей
стояли на отмеченных клетках.
Раскрасим доску в цветов по диагонали и её сдвигам, как на рисунке. Любой цвет образует расстановку из
ладей, не
бьющих друг друга. По принципу Дирихле среди
отмеченных клеток найдётся цвет, содержащий не менее
отмеченных
клеток,. Поставим ладьи на все клетки этого цвета — получим
ладей, и по меньшей мере
из них стоят на отмеченных
клетках.
![]()
Ошибка.
Попробуйте повторить позже
Фигура оборотень бьёт все клетки, находящиеся от неё через клетку слева, справа, сверху или снизу, а также бьёт клетку, на которой стоит.
Какое наименьшее количество оборотней необходимо поставить на клетчатую доску , чтобы эти фигуры били все клетки
доски?
Источники:
Подсказка 1
Оборотни на каких множествах клеток точно друг друга не бьют? Попробуем найти такие участки (множества клеток), на которых мы сможем оценить количество оборотней.
Подсказка 2
Оборотни, стоящие на квадрате 2*2, друг друга точно не бьют. Как, исходя из этого соображения, найти 4 множества клеток, которые замещают всю доску и в которых мы сможем оценить количество оборотней?
Подсказка 3
Рассмотрите множества клеток, получаемые всевозможными путями оборотня из каждой клетки углового квадрата 2*2. В каждом таком множестве по 16 клеток. Осталось лишь оценить количество оборотней в каждом таком множестве!
Раскрасим клетки доски в цвета следующим образом: все клетки, куда может прийти оборотень из, не умаляя общности, левой нижней
угловой клетки, покрасим в первый цвет. Сдвигами этого множества клеток вправо, вверх и вправо вверх получаем
множества
клеток.
![]()
Рассмотрим одно из них. Чтобы все клетки были побиты, нужно как минимум оборотня, так как каждый из них бьет не более
клеток, и, следовательно,
и меньше оборотней бьют максимум
клеток. Пример расстановки
оборотней: выделим
непересекающихся Т-образных фигур, в каждой из которых отметим по одному оборотню.
И так как оборотень, стоящий на клетке из одного множества, не может дойти до клеток из трех других, получаем, что всего нужно как
минимум оборотней.
Ошибка.
Попробуйте повторить позже
Таблица заполнена числами как показано на рисунке:
| 1 | 2 | 3 | … | 100 |
| 101 | 102 | 103 | … | 200 |
| | | | | |
| 9901 | 9902 | 9903 | … | 10000 |
Можно ли переставить некоторые числа так, чтобы в каждой клетке по прежнему стояло одно число, и чтобы во всех прямоугольниках из трех клеток сумма чисел не изменилась?
Источники:
Подсказка 1
Часто задачи с таблицами решаются раскрасками. А какая раскраска имеет какие-то приятные свойства для прямоугольников из трех клеток?
Подсказка 2
Диагональная в 3 цвета! Тогда в каждом прямоугольнике из 3х клеток будет каждый цвет. Тогда попробуем воздействовать на каждый цвет по отдельности так, чтобы сумма в таких прямоугольниках не изменилась.
Подсказка 3
Если в каких-то клетках прибавляем, в каких-то надо отнимать.
Рассмотрим раскраску таблицы в три цвета, как показано на рисунке:
| 1 | 2 | 3 | … | 1 |
| 2 | 3 | 1 | … | 2 |
| 3 | 1 | 2 | … | 3 |
| | | | | |
| 1 | 2 | 3 | … | 1 |
Если в исходной таблице к числам цвета 2 прибавить единицу, а из чисел цвета 3 вычесть единицу, то мы получим такую перестановку, что набор чисел сохранится. А сумма в каждой тройке тоже.
Ошибка.
Попробуйте повторить позже
Таблица заполняется по правилам игры “Сапёр
”: в некоторые клетки ставится по одной мине, а в каждой из остальных клеток
пишется количество мин во всех примыкающих к ней по стороне клетках. Какое наибольшее значение может принимать сумма всех
записанных чисел?
Пример. Черные клетки шахматной раскраски сделаем минами, а белые оставим пустыми.
Оценка. Клетки без мин будем называть пустыми. Покрасим внутренние ребра нашей таблицы: если ребро разделяет мину и пустую
клетку, покрасим ее в синий цвет, а иначе — в красный. Заметим, что в пустой клетке написано количество синих рёбер, прилегающих к ней,
а также то, что синее ребро прилегает ровно к одной пустой клетке. Отсюда следует, что сумма чисел в таблице равна количеству синих
ребер, а их в свою очередь не больше, чем ребер всего
Ошибка.
Попробуйте повторить позже
Какое наибольшее число квадратов можно разместить по линиям сетки (без перекрытий) внутри квадрата
Подсказка 1
Попробуйте придумать какой-нибудь простой пример. Это натолкнëт на оценку.
Подсказка 2
Итак, скорее всего, вы придумали пример на 25. При этом понятно, что 26-й квадрат добавить не получится, как бы ни были расставлены 25, потому что они всегда буду слишком близко друг к другу. Как более формально это доказать?
Подсказка 3
Попробуйте выделить 25 таких клеток, чтобы любой квадрат содержал ровно одну клетку.

Отметим некоторые клетки квадрата как на первом рисунке. Заметим, что любой квадрат
будет содержать в себе ровно
одну из отмеченных клеток. Но т.к. отмеченных клеток всего
то и квадратов
можно уместить не более
Пример на
квадратов
приведен на втором рисунке.

Ошибка.
Попробуйте повторить позже
Назовем кольцом клетчатую фигурку, полученную вырезанием из квадрата центрального квадрата
Каким наименьшим
количество колец можно целиком покрыть квадрат
Фигурки могут накладываться друг на друга, но не могут вылезать за пределы
доски.
Подсказка 1
Попробуйте придумать какой-то простой пример, это натолкнëт вас на оценку.
Подсказка 2
Скорее всего, вы придумали пример на 8. Подумайте, с помощью чего можно будет сказать, что более 8 колец быть не может?
Подсказка 3
Выделите 8 таких клеток, что каждое кольцо содержит ровно одну клетку.

Рассмотрим отмеченных на первом рисунке клеточек. Любое кольцо в этом прямоугольнике
будет накрывать
ровно одну из отмеченных клеточек. Тогда для покрытия всего квадрата понадобится хотя бы
колец. Пример на
колец такой: возьмем
кольца, как на второй картинке, и повернем эту конструкцию на
относительно центра
раза.
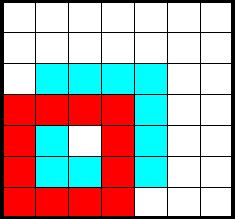
Ошибка.
Попробуйте повторить позже
Планета Тор представляет собой квадрат Столбцы и строки этого квадрата пронумерованы остатками
от деления
на
Искусственный спутник может наблюдать за четырьмя клетками с координатами
Какое наибольшее количество спутников можно отправить на орбиту планеты Тор так, чтобы все клетки наблюдались, и при выходе из
строя любого из спутников появлялась не наблюдаемая клетка?
Подсказка 1
Далее будем называть квадратом 2 * 2 все четверки с координатами (a,b), (a + 1, b), (a, b + 1), (a + 1, b + 1). Давайте начнем решение с примера. Для этого попробуйте придумать некоторую раскраску в два цвета так, чтоб было удобно работать с квадратами 2 * 2.
Подсказка 2
Давайте красить диагонали! Для начала будем считать, что диагонали из 120 клеток (следующая клетка диагонали, если мы в (a,b), совпадает c (a + 1, b + 1)). Как лучше красить диагонали?
Подсказка 3
Ага! Попробуем красить по две и пропускать две. Сколько тогда у нас закрашенных клеток?
Подсказка 4
Правильно! Ровно половина! За какими квадратами 2 * 2 лучше наблюдать спутникам?
Подсказка 5
Ага! Рассмотрим квадраты 2*2, у которых левая "нижняя" клетка черная, и пусть за каждым из них наблюдает спутник. Скольким квадратам мы выдали по спутнику?
Подсказка 6
Точно! Снова ровно половине. Теперь перейдем к оценке. Обозначим за s количество спутников. Попробуйте отметить уникальную клетку спутника и посмотреть на все вертикальные доминошки, которые их содержат. Оцените сверху количество вертикальных доминошек, которые лежат в двух квадратах 2 * 2, и посчитайте, сколько вертикальных доминошек лежат ровно в одном квадрате.
Подсказка 7
Попробуйте для начала посчитать, сколько вообще вертикальных доминошек, а еще поймите, сколько раз мы могли посчитать каждую доминошку.
Подсказка 8
Вертикальных доминошек 120²! Заметим, что в каждом квадрате 2 * 2 две вертикальные доминошки. Отсюда можно написать оценку сверху на s, используя прошлые оценки.
В решении будем называть квадратами все четверки с координатами
Аналогичное
определение введем для квадратов
Пример. Покрасим две соседние диагонали в черный цвет, в обеих диагоналях по клеток, так как нумерация циклическая, затем две
диагонали пропустим, далее снова красим две диагонали в черный цвет и т.д. В конце ровно половина всех клеток будет покрашена в
черный цвет. Возьмем все квадраты
у которых левая нижняя клетка черная, и пусть за каждым из них наблюдает спутник. Для
квадратов с левыми нижними углами в “нижней” черной диагональю уникальными клетками будут как раз эти углы, а для квадратов с
левыми нижними углами на “верхней” черной диагонали уникальными клетками будут их правые верхние углы. Понятно, что всего
выбранных квадратов ровно половина от общего количества.
Оценка. Обозначим количество спутников через Отметим для каждого спутника любую из его уникальных клеток и рассмотрим все
вертикальные доминошки, содержащие эти клетки. Заметим, что
из них принадлежат ровно одному квадрату
соответствующему
некоторому спутнику. Докажем, что есть хотя бы
вертикальных доминошек, не лежащих целиком ни в каком квадрате
для
некоторого спутника. Для каждой из отмеченных клеток есть хотя бы одна такая доминошка, покрывающая эту клетку. И каждую такую
доминошку мы посчитали не более
раз, так как в ней всего
клетки. Всего вертикальных доминошек
То есть у нас есть не
больше
вертикальных доминошек, лежащих в двух квадратах
и
доминошек, лежащих ровно в одном квадрате.
При этом в каждом квадрате
лежат ровно
доминошки. Тогда всего квадратов
соответствующих спутникам, не
больше
откуда то есть
Ошибка.
Попробуйте повторить позже
Докажите, что доску нельзя разрезать на
-тетрамино. Все виды
-тетрамино указаны на рисунке снизу.
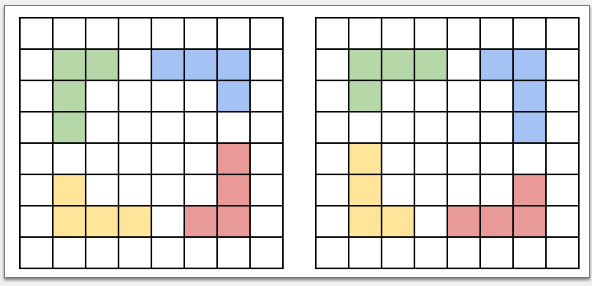
Подсказка 1
Давайте поймём, для чего мы в принципе используем раскраски и почему используем конкретную в задаче. Раскраска нужна, чтобы в большинстве случаев получить противоречие с какой-нибудь чётностью, количеством клеток определённого цвета и т.п. Значит, нам нужно различать клетки различных цветов в фигурке. Тогда какая раскраска нам тут может подойти?
Подсказка 2
Думаю, вы попробовали немного перебрать раскраски самостоятельно и понять, какая нам нужна. Здесь нам подойдёт полосатая раскраска. Например, почему не подойдёт шахматная? Потому что тогда у нас в фигурке будет 2 белые и 2 чёрные клетки, и мы их никак не различим. А как будут распределяться цвета в фигурке у нашей раскраски и почему же это решает задачу?
Подсказка 3
Верно, у нас будет 3 клетки одного цвета и одна другого цвета. Теперь давайте вспомним про чётность. Всего клеток каждого цвета у нас по 50 штук. А можем ли мы получить в принципе чётное число клеток одного из цветов? Осталось понять это, учитывая раскраску, и победа!
Предположим противное: что указанное разрезание возможно.
Покрасим доску в два цвета, чередуя черные и белые полоски. Заметим, что любая -тетрамино занимает
клетки одного цвета и
другого, а всего
-тетрамино в таком разрезании
штук.
Значит,
-тетрамино покроют нечетное количество белых клеток, а должны покрыть
— противоречие.
Ошибка.
Попробуйте повторить позже
Дно прямоугольной коробки покрыто плитками и
Одна плитка
потерялась. Можно ли вместо нее воспользоваться
плиткой
для покрытия дна коробки иным образом?
Подсказка 1
Сделаем такую раскраску, чтобы научиться отличать плитки разных типов!
Подсказка 2
Придумаем такую раскраску, чтобы каждый квадрат 2*2 покрывал нечетное количество черных клеток, а каждая полоска - чётное. Тогда, как и в практически всех задачах на раскраску, работает двойной подсчёт!
Раскрасим дно прямоугольной коробки в горошек как на рисунке с одной чёрной клеткой в каждом квадратике
![]()
Пусть всего получилось черных клеток. Каждый квадратик
покрывает ровно одну черную клетку, а каждая
плитка
—
или
черных клеток. Значит, четность числа
совпадает с четностью количества квадратиков
После того, как плитка потерялась, четность их количества изменилась. Но черных клеток в раскраске осталось столько же.
Значит, покрыть то же самое количество черных клеток по одному разу уже не получится, поэтому и все дно выложить иным образом
нельзя.
Нет, нельзя
Ошибка.
Попробуйте повторить позже
Дана клетчатая доска Каждая клетка доски покрашена в один из двух цветов: белый или чёрный. Назовём раскраску доски
уравновешенной, если в каждой строке и в каждом столбце 50 белых и 50 чёрных клеток. За одну операцию разрешается выбрать две строки
и два столбца так, чтобы из 4 клеток на их пересечении две были чёрными, а две — белыми, и перекрасить каждую из этих 4 клеток в
противоположный цвет. Докажите, что из любой уравновешенной раскраски можно получить любую другую уравновешенную раскраску с
помощью указанных операций.
Источники:
Подсказка 1
Непонятно, как доказывать, что возможно перевести любую уравновешенную раскраску в любую другую. Может, тогда докажем, что любую уравновешенную раскраску можно перевести в какую-то конкретную, тогда из любой мы будем приходить в неё и уходить в любую другую, совершая в обратном порядке действия, с помощью которых мы бы приходили к ней. Надо подумать, к какой раскраске мы будем приходить...
Подсказка 2
На ум приходит, конечно же, шахматная раскраска. Но переводить доску целиком в шахматную как-то тяжеловато. Может, начать со столбцов?
Подсказка 3
Разобьем наши столбцы на пары и будем по очереди красить их в шахматную раскраску. Возьмем сейчас самую левую пару столбцов, которая еще не покрашена нужным нам образом. Будем приводить горизонтальные доминошки к шахматной раскраске сверху вниз. Что делать, если в какой-то момент у нас доминошка, которая содержит оба цвета, неправильно стоит?
Подсказка 4
Пускай для определённости левая клетка нашей доминошки черная:
если она стоит неправильно, то сверху нее стоит доминошка, левая клетка которой так же черная. Посмотрим на доминошки, которые выше нашей, и видим, что в левом столбце суммарно чёрных клеток больше, чем в правом, ведь они покрашены в шахматную раскраску, где первая доминошка после нашей имеет слева чёрную клетку. Какой же вывод можно сделать из этого?
Подсказка 5
А вывод такой: в какой-то доминошке, которая находится ниже нашей, левая клетка будет белой, а правая чёрной, ведь иначе суммарно чёрных клеток будет больше в первом столбце, чем во втором, а это противоречит тому, что раскраска доски уравновешенная. Тогда мы можем применить к этим двум доминошкам операцию и продолжить спуск вниз. Но что же делать, если в какой-то момент, идя вниз по столбцам, мы найдём одноцветную доминошку?
Подсказка 6
Пускай она чёрная. Можно заметить, что тогда ниже нашей доминошки существует белая доминошка (иначе в сумме по этим столбцам чёрных клеток будет слишком много). Что мы можем тогда сказать про строки, которые содержат наши доминошки?
Подсказка 7
На самом деле эти строки содержат две клетки, которые находятся в одном столбце, который находится правее наших, и при этом верхняя будет белая, а нижняя черная (Назовем этот столбец S). Это верно в силу того, что левее наших столбцов в этих строках поровну черных и белых клеток. Тогда мы можем выбрать один из наших столбцов, столбец S и поменять цвет клеток в них по этим строкам. Как же завершить решение?
Подсказка 8
Можно заметить, что, когда мы совершали операции по смене цвета, мы не нарушали уравновешенность таблицы. А это значит, что можно продолжать раскрашивать пары столбцов дальше и прийти к шахматной раскраске.
Докажем, что из любой уравновешенной доски можно получить доску, раскрашенную в шахматную раскраску, причём на каждом шаге доска будет оставаться уравновешенной. Из этого будет следовать, что из любой уравновешенной доски можно получить любую другую, так как операция обратима.
Будем получать шахматную раскраску следующим образом. Разобьём столбцы на пары подряд идущих. Выберем самую левую пару столбцов и в этой паре столбцов по очереди будем приводить строки (состоящие из двух клеток) к шахматной раскраске. После того как закончим с первой парой столбцов, перейдём ко второй и так далее.
Объясним, как делать следующий шаг внутри одной пары столбцов и
Пусть в следующей строке
сейчас находятся чёрная и
белая клетка, но в неправильном порядке. Например, слева стоит чёрная клетка, а справа белая, а должно быть наоборот.
Заметим, что во всех строках выше
в первом столбце суммарно чёрных клеток не меньше, чем во втором, так как они уже
покрашены шахматным образом. Значит, в какой-то строке
ниже
должна быть ситуация, когда в левом столбце чёрных
клеток меньше, чем в правом, т.е. должна быть строка белая-чёрная (это следует из того, что суммарно в первом столбце
столько же чёрных клеток, сколько и во втором). Произведём операцию со строками
и
и текущими столбцами.

Пусть теперь у нас в строке стоят две одинаковые клетки, например чёрные. Тогда в какой-то строке
должны оказаться две
белые клетки (иначе суммарно чёрных клеток в этих двух столбцах будет слишком много). Понятно, что эта строка расположена ниже
текущей, т.к. выше неё все строки разноцветные. Теперь заметим, что если посмотреть на эту пару строк во всей таблице, то должен быть
столбец
правее
и
в котором в первой строке белая клетка, а во второй — чёрная. Тут мы пользуемся тем, что левее
наших столбцов в этих строках поровну чёрных и белых клеток. Теперь осталось лишь выбрать один из столбцов
или
(в котором неправильный цвет в строке
и столбец
а также строки
и
и произвести операцию с ними.

Легко видеть, что на каждом шаге уравновешенность доски сохраняется. А так как мы всегда можем сделать шаг в нашем алгоритме, то в конце получится шахматная раскраска.
Ошибка.
Попробуйте повторить позже
Таблица покрашена в несколько цветов (каждая клетка — ровно в один цвет) так, что в любом квадрате
присутствуют
клетки не более чем трёх различных цветов. Какое наибольшее количество цветов могло быть использовано?
Источники:
Подсказка 1
Раз у нас в каждом квадрате 2 на 2 не более трех различных цветов, то в каждом из них есть цвет, клеток которого хотя бы две в квадрате. Может, тогда стоит рассмотреть сколько может быть квадратов, в котором хотя бы две клетки конкретного цвета?
Подсказка 2
Попробуйте пойти таким путем: для начала найдите 4 квадратика, в которых по одной клетке такого цвета (а возможно их меньше, но считайте что 4), А после оцените кол-во квадратиков, в которых хотя бы 2 клетки этого цвета с помощью разного подсчета кол-ва клеток этого цвета во всех квадратиках)
Подсказка 3
В итоге выйдет хорошая оценочка на кол-во квадратиков, в котором конкретного цвета хотя бы 2. А теперь вспоминаем, что у нас все квадратики такие, что в них есть цвет, которого хотя бы два. Остается посчитать кол-во квадратов, предположить что цветов всего C, и пользоваться оценкой)
Подсказка 4
Если немного сложно пользоваться полученной оценкой, то попробуйте сложить все полученные оценки для всех цветов, а также вспомнить, что сумма всех кол-в клеток конкретного цвета - это кол-во всех клеток)
Оценка. Сначала сформулируем и докажем следующую лемму:
Лемма. Пусть — количество клеток некоторого цвета
Тогда существует не более
квадратов
в которых клеток
этого цвета хотя бы
Доказательство. Прежде всего отметим, что каждая клетка этого цвета находится в четырех квадратах Внимательный
читатель заметит, что эти квадраты могут выходит за границы доски, но поскольку мы оцениваем количество квадратов
в которых
клеток этого цвета хотя бы
сверху (даже если при оценке некоторые такое квадраты выходят за доску, то все равно оценка справедлива),
то это замечание не повлияет на доказательство. Рассмотрим самую левую клетку этого цвета, находящуюся на самой нижней горизонтали
доски, в которой есть этот цвет. Понятно, что квадрат, в котором эта клетка является правой верхней, не может больше содержать
клеток этого цвета. Аналогично для самой правой клетки нижнего ряда (которая, вообще говоря, может совпадать с самой
левой клеткой этого ряда) квадрат, в котором она является левой верхней, не может больше содержать клеток этого цвета.
Такие же рассуждения можно провести с самым верхним горизонтальным рядом (который, опять же, может совпадать
с самым нижним). Таким образом, есть хотя бы
квадрата
в которых присутствует только одна клетка цвета
Теперь рассмотрим все квадраты которые содержат цвет
Так как каждая клетка этого цвета находится в четырех квадратах,
то суммарно в них находятся
клеток цвета
(некоторые из квадратов, возможно, выходят за границы таблицы). Пусть количество
квадратов, в которых хотя бы две клетки этого цвета, равно
Тогда, так как есть хотя бы
квадрата
в которых присутствует
только одна клетка цвета
то получим:
Пусть количество цветов равно Существует ровно
квадратов
которые накладывают условие на цвета. Тогда
для каждого квадрата
должен найтись цвет, клеток которого в нём хотя бы
а из всего
то просуммируем
количество квадратов
в которых клеток цвета
хотя бы
для всех
и оценим их количество сверху, пользуясь
леммой:
Но так как каждая клетка покрашена в один цвет:
Значит,
Пример. Рассмотрим все возможные вертикальные полоски. В первой из них покрасим все клетки в различные цвета. Во второй - в один
и тот же новый цвет. В третьей - снова все клетки в новые различные цвета, потом снова в один новый цвет и так далее. При этом клеток в
полосках с нечётным номером всего а полосок с чётным номером ровно
поэтому различных цветов ровно
Также понятно, что в любом квадрате
встретятся две клетки из вертикальной полоски с чётным номером.
Значит, они будут одинакового цвета, т. е. цветов в каждом квадрате
будет не больше
(на самом деле, ровно
Ошибка.
Попробуйте повторить позже
Назовём клетчатый квадрат, каждая клетка которого покрашена в чёрный или в жёлтый цвет, гармоничным, если в нём количество чёрных
клеток отличается от количества жёлтых клеток не более чем на единицу. Сколькими способами можно раскрасить клетки таблицы
в чёрный и жёлтый цвета так, чтобы любой квадрат в этой таблице был гармоничным?
Источники:
Подсказка 1
Подумайте о том, сколько клеток каждого цвета должно быть в каждом квадрате 2х2. Попробуйте начать раскрашивать самую верхнюю строчку. Какие ограничения при этом накладываются на следующую строку?
Подсказка 2
Теперь попробуйте применить то же самое поведение на все последующие строчки. А при каких условиях раскраски первой строки она будет соответствовать условию? Что если найдётся подстрока, в которой разница цветных квадратов в которой больше 2?
Подсказка 3
Попробуйте обозначить количество подходящих раскрасок первой строки за x и выразить через него количество подходящих раскрасок для всей доски. И осталось только найти х!
Подсказка 4
Если всё ещё испытываете некое затруднение, попробуйте рассматривать в первой строке моменты, когда рядом идут две клетки одного цвета. Попробуйте разбить строку на блоки по 2 клетки и посчитать количество возможных вариантов.
Для начала заметим, что в каждом квадрате должно быть по две клетки каждого цвета. Рассмотрим раскраску самой верхней строки
квадрата. Предположим, что в ней есть какие-то две соседние клетки одинакового цвета. Тогда, рассмотрев квадрат
содержащий эти
клетки, получим, что две клетки под ними должны быть противоположного цвета. Если теперь сдвинуть этот квадрат на одну клетку
вправо, получим, что в левом столбце две клетки противоположного цвета, поэтому и в правом столбце клетки тоже должны быть
противоположного цвета. Сдвигая этот квадрат аналогично вправо и влево, получим, что вторая строка должна быть противоположна (по
цветам) первой.
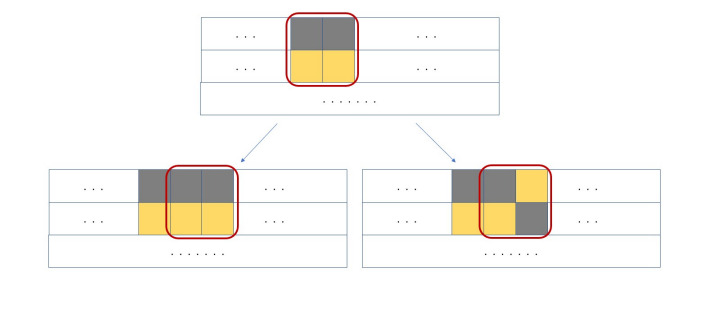
Если теперь проделать такие же рассуждения со второй и третьей строкой, получим, что третья строка должна быть противоположна
второй (т.к. во второй также найдутся две рядом стоящие клетки одного цвета). Аналогично далее строки будут чередоваться, и вся таблица
заполняется однозначно. Теперь поймём, при каких условиях на первую строку раскраска будет подходящей. Предположим, что в первой
строке найдётся подстрока, в которой клеток одного из цветов хотя бы на больше, чем другого. Такую подстроку можно сократить
до подстроки
длины
так, чтобы разница была ровно
(т.к. при отбрасывании одной клетки разница меняется на 1). Рассмотрим
квадрат
размера
содержащий подстроку
Так как в
разница между цветами равна
то
нечётно. Значит, в
квадрате
тоже разница между цветами будет равна
т.к. все его строки, кроме первой, можно разбить на пары
противоположных (понятно, что если в подстроке разница между цветами больше
то в ней найдутся две соседние клетки одного
цвета).
Таким образом, в первой строке не должно найтись подстроки, в которой клеток какого-то цвета хотя бы на больше, чем другого.
Предположим, что это условие выполнено, причём каждая строка, начиная со второй, противоположна предыдущей. Тогда в любом
квадрате чётного размера цветов будет поровну, а в любом квадрате нечётного размера количество клеток разных цветов будет отличаться
на
т.к. все строки в нём, кроме первой, разбиваются на пары, а в первой строке количество клеток разных цветов может отличаться
только на
Обозначим количество подходящих раскрасок первой строки за Тогда количество подходящих раскрасок всей доски будет равно
Действительно, в первой строке будет либо чередование цветов (
варианта), либо где-то встретятся две клетки
одинакового цвета. Во втором случае всё остальное определяется однозначно, а в первом всё определяется раскраской первого столбца (если
и в первой строке, и в первом столбце не будет двух стоящих рядом клеток одного цвета, то с помощью последовательного рассмотрения
квадратов
мы получим, что раскраска должна быть шахматной).
Теперь осталось найти Заметим, что трёх подряд идущих клеток одного цвета быть не может, т.к. эти три клетки уже дают
подстроку с разницей
Найдём в строке первый момент, когда рядом встретились две клетки одного цвета. Найдём следующий момент,
когда рядом встретятся две клетки одного цвета. Если это тот же самый цвет, то в минимальной подстроке, содержащей обе эти пары,
разница цветов будет равна
чего быть не может. Значит, это должны быть клетки другого цвета. Таким образом, блоки из пар клеток
одного цвета должны чередоваться, а ещё между этими блоками могут быть участки чётной длины из чередующихся клеток. Тогда
для расположения блоков может быть два варианта: либо их первые клетки расположены на нечётных местах, либо на
чётных.
В первом случае разобьём все клетки на пары подряд идущих. На месте каждой пары может быть либо блок из двух одинаковых клеток,
либо пара разных клеток. По набору мест блоков и цвету самой левой клетки цвета всех остальных клеток определяются однозначно. Таким
образом, вариантов в этом случае В случае, когда первые клетки блоков располагаются на чётных позициях, есть всего
мест для блоков, и цвета всех клеток также определяются наборами мест блоков и цветом самой левой клетки. В этом случае вариантов
При этом те варианты, где блоков вообще нет, мы посчитали дважды. Таких вариантов
(когда цвета чередуются). Значит,
Получаем ответ:
Ошибка.
Попробуйте повторить позже
На бесконечной клетчатой плоскости некоторые клетки покрашены в красный цвет, некоторые — в синий, а некоторые остались непокрашенными. Известно, что в каждой строчке, где есть хотя бы одна синяя клетка, есть также хотя бы 5 красных, а в каждом столбце, где есть хотя бы одна красная клетка, есть хотя бы 6 синих. Какое наименьшее положительное число покрашенных клеток может быть на плоскости?
Источники:
Подсказка 1
Для начала заметим, что мы можем избавиться от всех столбцов, в которых все клетки синие и от всех строк, в которых все клетки красные. Теперь в каждом столбце и строке у нас и синие, и красные клетки. Пусть у нас есть m строк и n столбцов ,x-кол-во красных клеток, y-кол-во синих клеток. По условию в каждом столбце хотя бы 6 синих клеток => y>=6n, аналогично x>=5m. В каждой строке есть хотя бы одна синяя клетка и 5 красных, n>=6.Аналогично m>=7.Чтобы догадаться до ответа, бывает полезно рассмотреть частный случай. Попробуйте рассмотреть случай, когда все закрашенные клетки будут находиться только на пересечении строк и столбцов.
—-----------
Подсказка 2
Так как m*n- все клетки при пересечении m строк и n столбцов , то m*n>=x+y>=5m+6n.Откуда следует, что m>=6n/(n-5). x+y>=5m+6n>=6n^2/(n-5). Теперь, считая производную, получаем, что x+y>=120 при n=10 и m=12. Заметим, что если мы возьмем n=10 и m=12 и клетки покрасим в шахматном порядке, то мы получим пример на 120. Логично предположить, что меньше 120 закрашенных клеток не может быть.
-----------—
Подсказка 3
Давайте рассмотрим два случая 1)x>=y 2)x<y. 1)Если x>=y>=6n =>в каком то столбце хотя бы 6 красных клеток, тогда в этом столбце хотя бы 6+6=12 закрашенных клеток => m>=12 => x>=60. Мы предположили , что x+y<120 => y<60. Попробуйте теперь что-нибудь сказать про n.
Подсказка 4
Так как n<=9 и x>=60, то в каком-то столбце >=7 красных клеток, тогда в каком-то столбце >=13 клеток, тогда m>=13 и x>=65 и y<55. Вам не кажется это похожим на предыдущий шаг? Попробуйте теперь сами сделать то же самое.
Подсказка 5
После нескольких таких шагов мы получим, что n<=5, но у нас n>=6. Противоречие! Со вторым случаем делаем то же самое. Оценка доказана. Значит, наш ответ 120.
Примеров для 120 закрашенных клеток несколько, они все отличаются перестановкой строк и столбцов. Можно взять прямоугольник
и раскрасить его в шахматном порядке в красный и синий цвет.
Докажем теперь, что меньше 120 закрашенных клеток не может быть.
Если в каком-то столбце есть закрашенные клетки, то по условию они либо только синие, либо обоих цветов. При этом, если в каком-то столбце все закрашенные клетки синие, можно превратить их все в незакрашенные. При этом условие задачи сохранится, а количество закрашенных клеток уменьшится (но не до нуля, так как в строчках с этими синими клетками останутся какие-то красные). Аналогичным образом можно избавиться от строчек, в которых есть красные клетки, но нет синих. Теперь можно считать, что во всех строчках и столбцах, где есть закрашенные клетки, присутствуют клетки обоих цветов.
Пусть у нас красных клеток и
синих, при этом закрашенные клетки находятся в
строках и
столбцах. Так как в каждом из
этих
столбцов присутствуют хотя бы 6 синих клеток, выполняется неравенство
или, что то же самое,
Аналогично,
или, что то же самое,
Также заметим, что в каждой строке есть хотя бы одна синяя клетка и 5 красных,
Аналогично
Сравним числа и
Пусть то есть
В каждом столбце присутствуют хотя бы 6 синих клеток. Из взятого в качестве предположения
неравенства следует, что в каком-то столбце количество красных клеток хотя бы
от количества синих, то есть хотя
бы 5, поэтому общее количество закрашенных клеток в данном столбце хотя бы 11, откуда
и, следовательно,
Если
и оценка доказана. Предположим,
тогда
то есть не превосходит
10.
Но раз а
в каком-то из наших не более чем 10 столбцов присутствуют хотя бы 6 красных клеток. Так как в нём должно
быть ещё и 6 синих, мы получаем, что общее количество закрашенных клеток в этом столбце хотя бы 12, то есть,
и
Тогда, чтобы
было меньше 120, необходимо
Продолжим эти рассуждения.
Поскольку значит
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 7 красных клеток, откуда
Поскольку в каком-то столбце присутствуют хотя бы
то есть хотя бы 8 красных клеток, откуда
Поскольку значит,
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 9 красных клеток, откуда
Поскольку значит,
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 11 красных клеток, откуда
Поскольку значит,
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 15 красных
клеток, откуда
Отсюда получаем, что
что противоречит доказанному
ранее.
Аналогично разбираем случай, когда то есть
В каждой строке присутствуют хотя бы 5 красных клеток. Из взятого в
качестве предположения неравенства следует, что в какой-то строке есть хотя бы 6 синих клеток, то есть общее количество закрашенных
клеток в данной строке хотя бы 11, откуда
и, следовательно,
Если
и оценка доказана. Предположим,
тогда
то есть не превосходит 10.
Но раз а
в какой-то из наших не более чем 10 строк присутствуют хотя бы 7 синих клеток. Так как в ней должно быть
ещё и 5 красных, мы получаем, что общее количество закрашенных клеток в этой строке хотя бы 12, то есть,
и
Тогда,
чтобы
было меньше 120, необходимо
Продолжим эти рассуждения.
Поскольку в какой-то строке присутствуют хотя бы
то есть хотя бы 8 синих клеток, откуда
Поскольку значит
Значит, в какой-то строке присутствуют хотя бы
то есть хотя бы 10 синих
клеток, откуда
Отсюда получаем, что
что противоречит доказанному
ранее.
Таким образом, мы разобрали оба случая и доказали, что ситуация, в которой невозможна.
Ошибка.
Попробуйте повторить позже
Доска покрыта фигурками трех типов, указанных на рисунке. Докажите, что фигурок первого типа не меньше
![]()
Занумеруем строки сверху вниз числами от
до
В строках с нечётными номерами занумеруем клетки слева направо цифрами
В остальных столбцах сделаем то же самое, но с цифрами
Заметим, что на доске по
клеток с цифрой
и
а с
остальными цифрами — по
Также заметим, что фигурки второго и третьего типов покрывают четыре клетки разного цвета, а
фигурка первого типа — только три. Следовательно, фигурками второго и третьего типа мы покроем не более
клеток с цифрой
(потому что каждая из них содержит клетку с
и
). Значит, оставшиеся
клеток с цифрой
мы должны
покрыть фигурками первого типа. Учитывая, что каждая такая фигурка покрывает не более одной клетки с цифрой
получаем
требуемое.
Занумеруем клетки как в предыдущем пункте. Нетрудно видеть, что всего имеется
клеток с
— с
— с
и
— с
Как мы выяснили раньше, фигурки второго и третьего типов покрывают по одной клетке с
каждой цифрой, а значит они покроют не более
клеток с каждой цифрой, а оставшиеся хотя бы
клеток с
с
и
с
должны покрыть фигурки первого типа. Заметим, что если фигурки второго и
третьего типов покрыли
клеток с
то фигурки первого типа должны покрыть
клеток с
с
и
с
(потому что фигурки второго и третьего типов покрывают по одной клетке с каждой
цифрой).
Нетрудно понять, что из фигурок первого типа, покрывающих клетки с
не более
покрывают клетки с
так
как каждый цвет покрывается фигуркой не более одного раза (всего есть
свободных клеток с
). Следовательно, есть хотя бы
фигурок первого типа, которые не покрывают клетку с
но покрывают с
Аналогично есть хотя бы
фигурок, которые
покрывают клетку с
но не покрывают клетку с
Из структуры раскраски понятно, что если фигурка первого типа не покрывает клетку с или
то она покрывает клетку с
Таким
образом, фигурки первого типа покрывают хотя бы
клеток с
Следовательно, фигурки второго и третьего типов покрывают не более
клеток с
Тогда по рассуждениям из предыдущего пункта получаем оценку на
что и
требовалось.
Ошибка.
Попробуйте повторить позже
Сколькими способами можно раскрасить клетки доски в три цвета так, чтобы все цвета были использованы и в каждом уголке из
трех клеток присутствовали ровно два цвета?
Подсказка 1
С уголком работать трудно, он не особо хорошо связан с квадратом 20×20. Попробуйте перейти от уголка к более простому объекту.
Подсказка 2
Этим объектом будет квадрат 2×2. Подумайте, как в нëм будут распределены цвета.
Подсказка 3
А теперь подумайте, какую часть квадрата 20×20 надо раскрасить, чтобы однозначно закрасить оставшуюся часть квадрата.
Заметим, что в каждом квадрате так же ровно
разных цвета, более того ровно по
клетки каждого. То есть раскрасив верхнюю
строчку (если только не все её клетки одноцветные) и самую левую клетку из второй строчки, мы однозначно раскрашиваем
весь оставшийся квадрат
или приходим в тупик и понимаем, что его раскрасить нельзя. Несложно заметить, что
мы не приходим в тупик, только если каждый столбец получается одноцветным. То есть количество способов раскрасить
квадрат равно количеству способов раскрасить первую строчку (но это ещё нужно умножить на
т.к. если первая строка
одноцветная, то мы рассмотрим первый столбец так же, как первую строку и получим аналогичный случай). Каждая клетка
первой строки покрашена в один из
цветов - это
вариантов, так как соседние строки в один цвет покрашены
быть не могут. Минус варианты, когда в ней нет всех трёх цветов, а это
(первые два цвета выбираются, дальше
чередование).



