Раскраски
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Можно ли разрезать доску на четырехклеточные фигуры типа Т?
Раскрасим доску в шахматную раскраску. Заметим, что фигура типа Т либо содержит одну белую и три чёрные клетки,
либо наоборот. Предположим, что разрезать можно. Пусть всего фигур первого типа, тогда фигур второго —
Количество белых клеток равно
то есть оно нечётно. С другой стороны их
а это чётное число,
противоречие.
Нет
Ошибка.
Попробуйте повторить позже
Можно ли разрезать доску на четырехклеточные фигуры типа Г?
Раскрасим клетки второй, четвёртой и шестой строки в чёрный цвет. Заметим, что в одну букву Г входит либо одна, либо три чёрные
клетки, то есть нечётное количество. Предположим, что разрезать можно. Всего будет фигур, то есть всего на доске
нечётное количество (сумма нечётного количества нечётных чисел нечётна) чёрных клеток. Однако всего
чёрных клеток,
противоречие.
Нет
Ошибка.
Попробуйте повторить позже
Можно ли разрезать доску с вырезанным уголком на прямоугольники
по линиям сетки?
Пусть вырезан левый нижний уголок (не умаляя общности). Раскрасим клетки в чёрный цвет как показано на рисунке:
![]()
Нетрудно понять, что один прямоугольник не может содержать более одной чёрной клетки. Значит, потребуется хотя бы
прямоугольника. Они займут хотя бы
клеток, а это больше, чем
то есть разрезать нельзя.
Нет
Ошибка.
Попробуйте повторить позже
В клетчатом квадрате по линиям сетки без наложений разместили
прямоугольников
Какая клетка могла оказаться
ненакрытой ни одним прямоугольником? (Найдите все варианты и докажите, что других нет).
Замечание. Текст решения ниже написан с ориентиром на белую тему. В тёмной теме цвета надо поменять местами.
_________________________________________________________________________________________________________________________________________________________________________________
Раскрасим чёрным цветом клетки как показано на картинке:
![]()
Заметим, что каждый прямоугольник обязан содержать ровно одну чёрную клетку. Всего чёрных клеток. Значит ненакрытой
останется какая-то чёрная клетка, а все белые точно будут накрыты.
А теперь покрасим в чёрный клетки по-другому:
![]()
Для этой раскраски справедливы вышеописанные рассуждения, то есть ненакрытая клетка является чёрной и на этом рисунке. Множества чёрных клеток с первой и второй картинки пересекаются по центральной клетке. Следовательно, ненакрытой может быть только она.
Осталось привести пример:
![]()
Центральная клетка
Ошибка.
Попробуйте повторить позже
При каких клетчатая доска
может быть раскрашена в два цвета так, чтобы каждая клетка граничила по стороне ровно с двумя
клетками не своего цвета?
Пусть цвета — черный и белый, и есть белых и с черных клеток. Посчитаем двумя способами число черно-белых двуклеточных
домино.
Каждая черная клетка входит ровно в две разноцветные доминошки, поэтому доминошек ровно , аналогично их
. Значит,
.
Общее число клеток четно, значит, и
четно. Осталось привести пример.
Разобьем доску на квадратики . Покрасим их в шахматном порядке. Затем, сдвинем раскраску на 1 по диагонали. Легко проверить,
что полученная раскраска подходит.
Ошибка.
Попробуйте повторить позже
В таблице некоторые
клеток покрашены в красный цвет, ещё
в розовый, а оставшиеся
— в синий. Известно,
что
у каждой граничной клетки есть хотя бы
соседа такого же цвета;
у каждой неграничной клетки есть хотя бы
соседа такого же цвета.
Какое наименьшее значение может принимать величина
(Клетка называется граничной, если она примыкает к границе таблицы. Соседями называются клетки, имеющие общую сторону.)
Источники:
Из условия легко понять, что у каждой клетки может быть не более одного соседа другого цвета.
Докажем, что раскраска таблицы должна быть «полосатой», то есть либо каждая строка, либо каждый столбец покрашены полностью в один цвет. Для этого достаточно показать, что либо все пары соседних клеток разного цвета являются соседями по горизонтали, либо все такие пары являются соседями по вертикали.
Рассмотрим любую пару соседних клеток разных цветов - если в таблице вообще есть клетки разных цветов, то такая найдётся. Остальные соседи этих клеток совпадают с ними по цвету, поэтому разделяющая цвета граница будет продолжаться в обе стороны, и далее, пока не упрётся в края таблицы:
![]()
Получаем, что любая граница между разными цветами должна идти от края до края таблицы, причём с каждой стороны от неё будет одноцветная полоса клеток. Но это означает, что вертикальная и горизонтальная границы одновременно существовать не могут. Следовательно, либо все границы горизонтальные, либо все границы вертикальные, и раскраска в любом случае «полосатая». (Ширина каждой полосы при этом должна быть не менее 2 клеток - впрочем, для решения это значения не имеет.)
Это означает, что либо количества клеток каждого цвета делятся на высоту таблицы, либо на её ширину, как и разность . С другой
стороны, эта разность не может быть равна 0 , так как в этом случае
и общее количество клеток равно
, но на 3 число
не делится. Значит,
или
.
Равенство возможно, если красные клетки занимают 12 столбцов (по 28 клеток), розовые столько же, а синие - 11 столбцов.
Если столбцы одного цвета расположить подряд, то все условия задачи будут выполнены.
Ошибка.
Попробуйте повторить позже
Клетки таблицы окрашены в белый цвет. За один ход разрешается выбрать любые
клеток из одной строки или из одного
столбца и перекрасить каждую из них в противоположный цвет — из белого в черный, а из черного в белый. За какое наименьшее
количество ходов можно получить таблицу с шахматной раскраской клеток?
Источники:
Подсказка 1
Рассмотрим полученную шахматную раскраску. Раз перекрашиваем мы изначально белую доску, то оценивать кол-во ходов нужно количеством чёрных клеток в какой-то части нашей доски, где окрашивание одной клетки никак не влияет на цвет другой.
Подсказка 2
Посмотрим на диагональ, покрашенную в чёрный цвет. В ней 100 чёрных клеток, и при перекрашивании одной из них мы никак не меняем окрас другой. А значит, всего было сделано >= 100 ходов. Теперь попробуем привести пример на 100.
Подсказка 3
Попробуем в столбцах под номерами вида 2n+1 не красить клетку с номером 2n+1. То же самое сделаем со строками. Попробуйте доказать, что в этом случае мы получим шахматную раскраску.
Оценка.
Покажем, что ходов обязательно придётся сделать.
Первый способ. Предположим, что мы получили шахматную раскраску. Рассмотрим диагональ, покрашенную в чёрный цвет. За ход
можно перекрасить не более одной клетки этой диагонали, следовательно, потребовалось не менее ходов.
Второй способ. Предположим, что мы сделали менее ходов. Тогда найдётся строка, которую мы не задействовали. Но в этой строке
в результате появилось
чёрных клеток, значит, было сделано как минимум
“вертикальных” ходов. Аналогично показывается, что
было сделано как минимум
“горизонтальных” ходов, т.е. всего не менее
ходов.
Пример.
Покажем, как за ходов можно получить шахматную раскраску, для этого перекрасим первый столбец без первой клетки, третий
столбец без третьей клетки, пятый столбец без пятой клетки,
й столбец без
й клетки. Дальше перекрасим первую строку без
первой клетки, третью строку без третьей клетки, пятую без пятой клетки,
ю строку без
й клетки. Тогда все клетки, у
которых номер строки и номер столбца имеют разную чётность, окажутся переркашенными ровно один раз и, значит, чёрными, а остальные
клетки будут белыми.
ходов
Ошибка.
Попробуйте повторить позже
В некоторых клетках прямоугольной доски размера на
сидят по одной черепашке. Каждую минуту каждая из них одновременно
переползает в одну из клеток доски, соседнюю с той, в которой они находятся, по стороне. При этом, каждый следующий ход
делается ими в направлении, перпендикулярном предыдущему: если предыдущий ход был горизонтальным — налево или
направо, то следующий будет вертикальным — вверх или вниз, и наоборот. Какое максимальное количество черепашек может
перемещаться по доске неограниченное время так, что в каждый момент в каждой клетке будет находиться не более одной
черепашки?
Источники:
Подсказка 1
Задачка на оценку+пример, попробуем тогда сначала придумать какой-нибудь пример, а дальше, отталкиваясь от него, догадаться до оценки! Какие мы можем придумать простейшие траектории черепашек, удовлетворяющие условиям задачи?
Подсказка 2
Самое простое, что можно придумать — заставить черепашек двигаться по циклам в квадратах 2*2. Сколько тогда двигающихся по таким траекториям черепашек мы можем разместить на поле?
Подсказка 3
После того, как мы придумали пример, переходим к оценке. По условию черепашки при каждом шаге поворачивают на 90 градусов. Тогда на каком поле относительно начального черепашка окажется после одного шага, двух шагов? Исходя из этих соображений, как можно покрасить поле так, чтобы у движения черепашки были удобные ограничения относительно этой раскраски?
Подсказка 4
Поле можно раскрасить в 4 цвета “в горошек”, и из-за того, что длины сторон поля нечётные, количество клеток разных цветов не будет одинаковым. А черепашка двигается по этой раскраске так, что обязательно проходит по циклу все 4 цвета. Осталось лишь посчитать количество клеток разных цветов и из этого получить оценку!
Сначала покажем, что черепашек могут так перемещаться. Выделим в верхнем левом углу прямоугольник
Поставим в
каждую его клетку по черепашке. Разобьем его на квадратики
И пусть в каждом квадратике черепашки перемещаются по циклу
против часовой стрелки. Тогда все черепашки всегда смогут сделать ход.
Докажем, что большего количества черепашек быть не может. Раскрасим нашу доску в цвета в горошек (в первой строке чередуются
цвета
и
во второй —
и
в третьей — снова
и
и так далее). Заметим, что клеточек цвета
ровно
Рассмотрим клеточки второго цвета. Заметим, что все черепашки на клеточках второго цвета через
хода попадут в клеточки четвертого
цвета. Тогда в данный момент черепашек на клеточках второго цвета не больше, чем черепашек на клеточках четвертого цвета, то есть
также не больше, чем
Нам осталось оценить сверху количество черепашек, стоящих в данный момент на клеточках первого и
третьего цвета. Чтобы это сделать, достаточно подождать один ход, тогда все эти черепашки попадут на клеточки второго и
четвертого цвета. А затем проделать те же самые рассуждения. То есть всего черепашек действительно не больше, чем
Ошибка.
Попробуйте повторить позже
На клетчатой бумаге выложен из спичек квадрат (на границе между двумя клетками лежит спичка длины 1 , длина стороны
клетки тоже равна 1). За один ход Петя может выбрать узел, из которого (в данный момент) исходят 3 или 4 спички, и убрать две спички,
выходящие из этого узла и образующие отрезок длины 2. Какое наименьшее количество спичек может остаться после некоторого количества
петиных ходов?
Источники:
Пример.
Пронумеруем спичечные столбцы и строчки таблицы от 1 до
. Сначала уберём все спички на границе. Затем уберём по 2
верхние спички 2 -го, 4 -го, . .
-го столбцов. Затем во 2 -й строчке уберём
спичек (
отрезок длины 2 ) так, чтобы остались
спички по краям. Затем уберём по 2 спички из 3 -го, 5 -го, ...,
-го столбцов так, чтобы сверху осталось по одной спичке в этих
столбцах. Далее уберём все спички 3 -й строчки. Затем уберём по 2 верхние спички чётных столбцов, затем
средних спичек 4 -й
строчки, затем верхние спички внечётных столбцах, а затем все спички 5-й строки. Будем дальше продолжать этот алгоритм, несложно
убедиться, что останутся только крайние спички в нечётных столбцах (не считая 1 и
) и чётных строках, в итоге
.
Оценка
Первый способ.
Выделим на границе квадрата единичные квадратики через один, как показано на картинке. Для каждого такого квадратика из четырех
спичек, образующих его, покрасим те спички, которые не лежат на границе квадрата (так, в двух выделенных угловых
квадратиках покрашены по две спички, а в остальных выделенных квадратиках по три). Заметим, что для каждого выделенного квадратика
мы не сможем убрать все покрашенные спички. Действительно, чтобы убрать такую спичку, в качестве узла надо брать вершину
квадратика
, не лежащую на границе квадрата
(а таких вершин на 1 меньше, чем покрашенных спичек в
), и при
этом нельзя использовать один и тот же узел дважды, и нельзя убрать две покрашенные спички квадратика
одних
ходом.
Таким образом, в конце останется хотя бы по одной покрашенной спичке в каждом из выделенных квадратиков.
Второй способ.
Покрасим синим все спички, которые не лежат на границе квадрата . Всего покрашено
горизонтальных и вертикальных
рядов по
спичек. Итого, у нас
синих спичек.
Заметим, что узел можно выбирать в качестве середины отрезка из двух спичек не более одного раза. При этом синюю спичку можно
убрать только если выбран узел, не лежащий на границе квадрата . Таких узлов
, а значит, мы уберем не более
спичек. Таким образом, в конце останется не менее
синих спичек.
Ошибка.
Попробуйте повторить позже
В какое минимальное число цветов достаточно покрасить клетки доски так, чтобы любые две клетки, связанные ходом ферзя, были
разного цвета? Напомним, что ферзь ходит на любое число клеток по вертикали, горизонтали и диагонали.
Источники:
Сразу можно сказать, что цветов хотя бы , так как все клетки в нижней строке должны быть покрашены в разные цвета. Давайте
покрасим первую строчку в цвета от 1 до
по порядку. А каждую следующую строчку будем красить со сдвигом на 2. По вертикали и
горизонтали клетки одного цвета друг друга бить не будут.
Нужно проверить, что клетка цвета в последней строке не окажется под боем клетки цвета
в первой строке. Пусть
— номер
строки, больший 1, тогда клетка цвета
в этой строке стоит в
столбце. Значит, в последней строке клетка цвета
стоит в
столбце (1).
Теперь заметим, что если у цвета не было перехода через границу, то очевидно, что по диагонали клетки одного цвета друг друга не
бьют. А если переход был, то между клеткой цвета в первой строке и в последней строке есть столбец (это следует из (1)),
ну тогда и в этом случае по диагонали клетки одного цвета друг друга не бьют, значит, приведенная раскраска таблицы
подходит.
Ошибка.
Попробуйте повторить позже
Даны натуральные числа . Паша и Вова играют в игру на доске
. Паша ходит первый. Они по очереди ставят бортики
длиной 1 на границе двух соседних клеток. Проигрывает тот игрок, после хода которого нельзя добраться из левой нижней клетки в правую
верхнюю, передвигаясь в соседние по стороне клетки (через бортики перепрыгивать нельзя!). Кто из игроков может выиграть, как бы ни
играл соперник?
Источники:
Рассмотрим ситуацию “за ход до проигрыша”, т. е. в которой невозможно сделать ход, чтобы не проиграть.
Так как в этой ситуации игра еще никем не проиграна, имеется путь по различным клеткам
, где
левая
нижняя клетка,
правая верхняя клетка, а
и
пара соседних по стороне клеток для каждого
. Заметим, что на
границах между клетками
нет бортиков, а на всех остальных
границах должны стоять бортики,
иначе в данной ситуации мог быть сделан ход, после которого остается путь
, в противоречие с выбором ситуации "за ход до
проигрыша".
Итак, к этому моменту было сделано ходов. Покажем, что
четно. Это будет означать, что в ситуации "за ход до
проигрыша"может оказаться только Паша. Значит, у Вовы всегда есть ход, не ведущий к немедленному проигрышу, и поскольку игра
завершится за конечное число ходов, Вова сможет победить.
Раскрасим клетки доски в шахматном порядке. Клетки и
одноцветные, если
и
одной четности, и разноцветные в противном
случае. При движении по пути
при каждом переходе в соседнюю клетку цвет меняется. Значит, четность количества переходов,
необходимых чтобы добраться из
в
, совпадает с четностью
. Тогда
четно, поэтому
также четно, что и требовалось.
Ошибка.
Попробуйте повторить позже
В каждую клетку шахматной доски записали некоторое натуральное число, не превосходящее
Сказочная шахматная фигура
кузнечик стоит в одной из угловых клеток. Каждым своим ходом кузнечик может прыгнуть в клетку, стоящую в той
же горизонтали или вертикали, что и кузнечик, и отстоящую от кузнечика на столько клеток, какое число записано в
клетке с кузнечиком (в частности, если в клетке с кузнечиком записано число
он может переместиться на одну из
соседних с ним по горизонтали или по вертикали клеток). Известно, что за
прыжка кузнечик может посетить все
клетки доски, побывав в каждой ровно один раз. Какое наибольшее количество троек могло быть написано в клетках
доски?
Источники:
Подсказка 1
Почему во всех клетках доски не могут быть написаны тройки?
Подсказка 2
В какой клетке не находился бы кузнечик, он сможет прыгать только в соседние через 2, а значит, посетит лишь множество из каких-то 8 клеток доски. Как можно продолжить данные рассуждения, чтобы получить оценку?
Подсказка 3
Можно разбить доску на попарно непересекающиеся множества клеток, так что все клетки каждого из множеств не могут быть равны 3. Сделайте это.
Подсказка 4
Получилось 8 множеств. Таким образом, в каждом множестве есть по крайней мере одна тройка, а значит, их количество не больше 56. Осталось придумать пример. Подумайте, как полученная оценка позволяет это сделать.
Разобьём клетки доски на группы, как показано на рисунке (разными цифрами обозначены разные группы). Заметим, что если в
какой-либо группе клеток все написанные числа равны трём, то кузнечик, прыгая по клеткам этой группы, никогда не сможет попасть в
клетки другой группы. Так как кузнечик может обойти все клетки доски, он смог переместиться между клетками разных групп хотя бы
раз. Значит троек могло быть не более
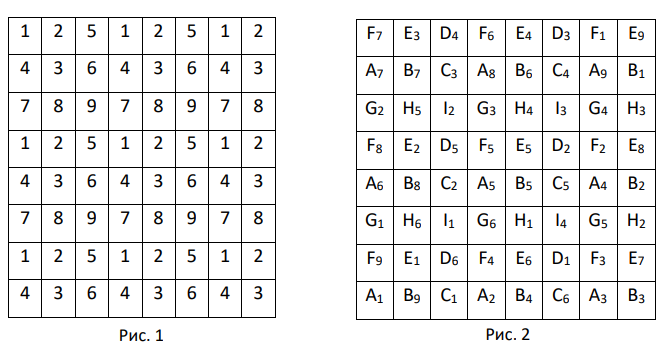
Приведём пример заполнения клеток таблицы и порядка обхода этих клеток кузнечиком (см. рисунок В клетках
стоят единицы, во всех остальных — тройки. Порядок обхода
по
возрастанию индексов.
Ошибка.
Попробуйте повторить позже
Дано натуральное число . В белой таблице
некоторые клетки покрашены в черный цвет. Известно, что при любом
натуральном
, таком что
, в каждом клетчатом прямоугольнике площади
есть хотя бы одна черная клетка.
Докажите, что в любом клетчатом прямоугольнике площади
тоже есть черная клетка.
Источники:
Подсказка 1
Очень хочется найти в каждом таком прямоугольнике прямоугольник площади k из условия. Как это можно сделать?
Подсказка 2
Давайте представим n²+n в виде a⋅b - произведение его сторон. Докажите, что меньшая из сторон не больше чем n) Чем это нам поможет?
Подсказка 3
Тем, что можно отрезать одну полоску 1⋅(длина меньшей стороны)! Поймите, что у нас получится нужный прямоугольник
Пусть , где
— длины сторон прямоугольника, тогда
, действительно, если это не так, то
Отрежем от прямоугольника полоску , площадь которой равна
, откуда
.
По условию в таком прямоугольнике
(понятно, что
, ведь иначе
) есть чёрная клетка, значит,
она была и в исходном.
Ошибка.
Попробуйте повторить позже
Каждая клетка таблицы окрашена в один из трех цветов: синий, красный или желтый. При этом в каждой строке таблицы число
красных клеток не меньше числа синих клеток и не меньше числа желтых клеток, а в каждом столбце таблицы число синих клеток не
меньше числа красных клеток и не меньше желтых клеток. Сколько желтых клеток может быть в такой таблице? Приведите пример
соответствующей раскраски.
Источники:
Подсказка 1!
1) Так-с, у нас есть свойство, верное для каждой строки. Давайте попробуем из этого сделать условие для количества клеток разных цветов во всей таблице уже.
Подсказка 2!
2) Да, мы поняли, что во-первых красных не меньше синих во всей таблице, а синих не меньше красных. Что же это значит.........
Подсказка 3!
3) В точности, значит, что их одинаково! А одинаково ли их в каждой строке.... Попробуйте разобраться!
Подсказка 4!
4) А теперь попробуйте доразбираться с точным количеством клеток каждого цвета!
Применяя первое условие для каждой строки, получаем, что красного цвета не меньше, чем синего, и не меньше, чем жёлтого. С другой стороны, из второго условия число синих клеток не меньше, чем желтых и красных. Отсюда число красных равно числу синих.
Пусть в каком-то столбце синих строго больше, чем красных. Тогда во всей таблице их также больше, что невозможно, значит, равенство числа синих и красных выполнено в каждой строке и каждом столбце.
Итак, в каждом столбце по синих и красных (и
жёлтая, иначе жёлтых станет больше, чем других цветов). Отсюда следует, что
жёлтых может быть только
При этом в каждой строке либо по
синих и красных клетки, либо всех цветов поровну, откуда
нетрудно построить пример.
| Ж | Ж | К | К | С | С |
| С | С | Ж | Ж | К | К |
| К | К | С | С | Ж | Ж |
| С | С | К | К | К | С |
| К | К | С | С | С | К |
Ошибка.
Попробуйте повторить позже
Некоторые клетки доски отмечены. Назовем клетки соседними, если они имеют общую сторону. Оказалось, что у каждой клетки
есть, по крайней мере, один отмеченный сосед. Доказать, что есть клетка, у которой, по крайней мере, два отмеченных
соседа.
Источники:
Подсказка 1
Нужно придумать раскраску, которой мы красиво сможем покрыть нашу доску. Предположим противное. Понятно, что для любой раскрашенной клетки существует ровно одна отмеченная рядом. Какую раскраску можно придумать, чтобы одна отмеченная клетка соответствовала двум раскрашенным?
Подсказка 2
Раскрасим диагонали в каждом квадрате 11*11. Скольким раскрашенным клеткам должна соответствовать каждая отмеченная клетка? Осталось лишь найти противоречие с нашей раскраской ;)
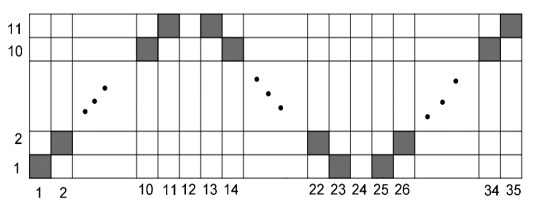
Раскрасим диагонали в каждом квадрате , как на рисунке выше. Мы покрасили
клетки и для каждой из них должна быть
ровно одна отмеченная рядом. Заметим, что любая соседняя для любой раскрашенной клетки является соседней ещё для
ровно одной раскрашенной, то есть любой сосед будет общим для каких-то двух раскрашенных клеток. Но раз так, то
каждая отмеченная будет ровно одна на две раскрашенные и покрашенные клетки должны разбиться на пары. Поскольку
их
, то такое невозможно и среди этих клеток найдётся хотя бы одна с хотя бы двумя отмеченными соседями, что и
требовалось.
Ошибка.
Попробуйте повторить позже
У Васи есть карточек трёх цветов, карточек каждого цвета не больше
Докажите, что он может выложить из них квадрат
так, чтобы любые две соседние (по стороне) карточки оказались разного цвета.
Источники:
Подсказка 1
Будем называть места для карточек клетками. Кажется, что больше всего проблем из-за тех карточек, которых больше всего, потому что они будут встречаться чаще. Может тогда сначала решим проблему соседних одноцветный для них?
Подсказка 2
Пусть наши цвета: красный, синий, зелёный — а их количества К, С, З соответственно. Не умоляя общности будем считать, что K ≥ С ≥ З. Разберёмся сначала с красными. В какой одной из самых известных раскрасок одноцветные точно не соседние?
Подсказка 3
Именно! Прекрасная шахматная раскраска. Попробуем применить эту же идею в нашей задаче. Как тогда нам следует размещать красные карточки?
Подсказка 4
Да! Не умоляя общности, в чёрные клетки шахматной раскраски. Только делать нужно это упорядоченно, а не случайным образом. Как же это сделать?
Подсказка 5
Например, идя по строкам слева направо и по столбцам сверху вниз, начиная с левого нижнего угла (как змейка, сначала нижняя строка, потом над ней и т.д.). Очевидно, что чёрных клеток хватит (вспомним условие). Отлично, с красными разобрались. Теперь логичнее всего разобраться с синими. Подумайте, как разместить их.
Подсказка 6
Ну, можно например делать также, как с чёрными, только начать с самой левой нижней белой клетки. Только вот что там будет наверху квадрата? Может быть там потом зелёные станут соседними. Не годится. Как бы нам сделать так, чтобы после расставления синих, соседних клеток не осталось вообще? Напомним, что C = min(К, С, З) и К + С + З = 100.
Подсказка 7
Будем раскладывать синие, симметрично красным! То есть начнём с правого верхнего угла и пойдём по белым. Знаем, что K + C ≥ 67. Что теперь происходит с квадратом?
Подсказка 8
Синяя и красная змейка не оставляют за собой соседних незанятых клеток. Докажите, что в итоге эти змейки "схлопнуться" и не оставят таких клеток вообще. А дальше останется сказать пару слов про зелёные. У вас всё получится! Успехов!
Пусть для определённости карточки были красного, синего и зеленого цветов и меньше всего было карточек зелёного цвета. Тогда зелёных
карточек не более Покрасим клетки квадрата
в шахматном порядке так, что левый нижний угол квадрата
чёрный. Начнём раскладывать красные карточки на черные клетки, начиная с левого нижнего угла квадрата. Сначала
будем заполнять слева направо чёрные клетки из нижней строки, затем также слева направо чёрные клетки из второй
снизу строки и т.д. до тех пор, пока не разложим все красные карточки. Далее разложим синие карточки на белые клетки,
начиная с левого верхнего угла доски. Сначала будем заполнять слева направо белые клетки из верхней строки и т.д. до тех
пор, пока не разложим все синие карточки. На оставшиеся клетки разложим зелёные карточки. Покажем, что никакие
зелёные карточки не могут оказаться рядом (для красных и синих карточек это очевидно). Поскольку красных и синих
карточек вместе не менее
штук, а в строке лежит не более пяти карточек каждого из этих цветов, количество строк,
занимаемых красными карточками, и количество строк, занимаемых красными карточками, вместе не меньше
Поэтому есть
строка, которая целиком заполнена красными и синими карточками. Но тогда зелёные карточки над этой строкой лежат на
белых клетках (и значит, не рядом), а зелёные карточки под этой строкой лежат на чёрных клетках(и значит, тоже не
рядом).
Ошибка.
Попробуйте повторить позже
Натуральные числа записаны в клетках таблицы
так, что для всех
числа
и
находятся в
соседних по стороне клетках. Каково максимальное значение возможной суммы чисел на главной диагонали?
Подсказка 1
Так-с, ну пример здесь приводить трудновато. Начнём с оценки. Возможно нам нужна раскраска... Действительно, соседние клетки отличаются на 1. Какая же раскраска будет полезна? Да, точно, в данном случае нам пригодится шахматная раскраска!
Подсказка 2
Давайте подумаем насколько большим может быть минимальное число на диагонали. В одной из сторон от диагонали лежит 1...Чуть чуть ещё поразмыслив, получаем оценку на число 26.
Подсказка 3
А как оценить остальные числа на диагонали? Они должны быть одной чётности, значит легко можно получить оценку на чётные числа от 52 до 64. Пример тоже придумать не так сложно!)
Оценка. Раскрасим клетки таблицы в шахматном порядке так, чтобы клетки на выбранной главной диагонали были белыми. Не умаляя
общности, можно считать, что единица стоит не выше диагонали. Найдем максимальное значение наименьшего числа, попавшего на
диагональ. Поскольку соседние числа стоят в клетках разного цвета, а белых клеток под диагональю находится всего то одно из чисел
от
до
обязательно попадает на диагональ. Остальные числа на диагонали гарантированно имеют одну четность, поэтому их сумма
не превосходит суммы четных чисел от
до
В итоге заключаем, что для суммы чисел на диагонали есть оценка
сверху:
Пример подходящей расстановки:

Ошибка.
Попробуйте повторить позже
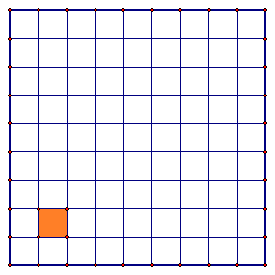
В квадрате вырезали клетку так, как показано на рисунке. Можно ли оставшуюся часть разрезать на четырехклеточные фигурки в
виде буквы Г? Фигурки можно поворачивать и переворачивать.
Источники:
Раскрасим вертикали с четными номерами в черный цвет, а с нечетными номерами — в белый. При этом количество клеток
каждого цвета будет нечетным. Одно Г-тетрамино занимает нечетное количество клеток каждого цвета, поэтому общее
количество тетрамино должно быть нечетным. Но с другой стороны их должно быть — четное количество,
противоречие.
Нет, нельзя
Ошибка.
Попробуйте повторить позже
Шахматная фигура клон делает ходы слона и коня в таком порядке: сначала она делает один ход как слон, затем — два хода как конь,
потом снова один ход как слон, затем два хода — как конь, и так далее. Какое наибольшее число клеток доски может обойти
клон, не побывав ни в какой клетке дважды? Начинать клон может с любой клетки, и эта клетка также будет считаться
пройденной.
Источники:
Оценка. Раскрасим доску в шахматном порядке. Пусть, не умаляя общности, клон начинает путь с белой клетки. Тогда цвета его клеток идут в таком порядке: Б-Б-Ч-Б-Б-Ч-Б-Б-Ч и т. д. В самом деле, за два хода как конь клон возвращается на клетку белого цвета и делает лишний ход Б-Б. Поэтому после 27 посещенных клеток клон пройдет по всем белым клеткам, и перейти на 28-ю клетку (а она тоже должна быть белого цвета) не сможет.
Пример приведен на картинке, клетки пронумерованы в порядке обхода клона, клетка с номером один — та, с которой он начинает.
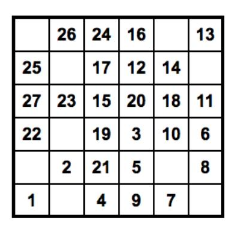
клеток
Ошибка.
Попробуйте повторить позже
Клетки прямоугольника раскрашены в три цвета: красный, синий и зеленый. Клеток каждого цвета по
штук. Назовем
доминошкой прямоугольник
Известно, что красно-синих доминошек нет. Какое наибольшее число разноцветных доминошек может
быть в таком прямоугольнике? Доминошки могут пересекаться.
Источники:
Оценка. Заметим, что в любой разноцветной доминошке одна из клеток зеленая. При этом каждая из зеленых клеток может давать
как максимум три разноцветных доминошки, поэтому всего разноцветных доминошек не более
Пример на доминошек получается, если покрасить центральный прямоугольник
шахматной раскраской в белый и
зеленый цвета, после чего перекрасить все белые клетки левее середины прямоугольника в синий цвет, а правее — в красный
цвет.
доминошек


.jpg)

