Тема Задачи №17 из ЕГЭ прошлых лет

№17 из ЕГЭ 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#30809Максимум баллов за задание: 3

Биссектриса $BB1$ и высота $CC1$ треугольника $ABC$ пересекают описанную около него окружность в точках $M$ и $N$ соотвественно. Известно, что угол $BCA$ равен $85∘$ и угол $ABC$ равен $40∘.$

а) Докажите, что $BM = CN.$

б) Пусть $MN$ и $BC$ пересекаются в точке $D.$ Найти площадь треугольника $BDN,$ если его высота $BH$ равна 7.

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

а) Найдем угол $BAM.$ Заметим, что $∠BAM = ∠BAC +∠CAM.$ Углы $CAM$ и $CBM$ опираются на одну дугу, значит, $∠CAM =∠CBM.$ По условию $BB1$ — биссектриса угла $ABC,$ равного $40∘,$ следовательно, $∠CBM = ∠ABM = 20∘.$

По условию $∠ABC = 40∘$ и $∠BCA =85∘,$ значит, по сумме углов в треугольнике $ABC :$

∠BAC = 180∘− ∠ABC − ∠BCA = 180∘− 40∘ − 85∘ = 55∘ ⇒ ⇒ ∠BAM = ∠BAC + ∠CAM = 55∘+ 20∘ = 75∘

Найдем угол $NBC :$

∘ ∠NBC = ∠NBA + ∠ABC = NBA +40

$PIC$

Углы $NBA$ и $NCA$ опираются на одну дугу, значит, $∠NBA = ∠NCA.$ Рассмотрим прямоугольный треугольник $ACC . 1$ По условию $∘ ∠AC1C = 90,$ следовательно, по сумме углов треугольника $ACC1 :$

∘ ∘ ∘ ∘ ∠NCA =∠C1CA = 180 − 90 − 55 = 35 ⇒ ⇒ ∠NBC = ∠NBA +40∘ = ∠NCA + 40∘ = 35∘+ 40∘ = 75∘

Тогда дуги $BM$ и $CN$ равны, значит, равны и хорды, стягивающие их, то есть $BM = CN.$

б) Заметим, что $∠DNB = ∠MNB = ∠MAB,$ так как они опираются на одну дугу $BM.$ Тогда треугольник $BDN$ является равнобедренным с углами $∘ ∠DNB = ∠DBN = 75$ и $DN =DB.$ Тогда по сумме углов треугольника $∠BDN = 30∘.$

Рассмотрим треугольник $BHD.$ В нем $∠BHD = 90∘,$ а $∠BDH = 30∘,$ то есть это прямоугольный треугольник c углом $30∘.$ Значит, в треугольнике $BHD$ имеем $DB = 2BH = 2⋅7= 14,$ а в треугольнике $BDN$ имеем $DN = DB = 14.$ Тогда

1 1 SBDN = 2 ⋅DN ⋅BH = 2 ⋅14 ⋅7= 49

$PIC$

Ответ:

б) 49

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а),	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#30810Максимум баллов за задание: 3

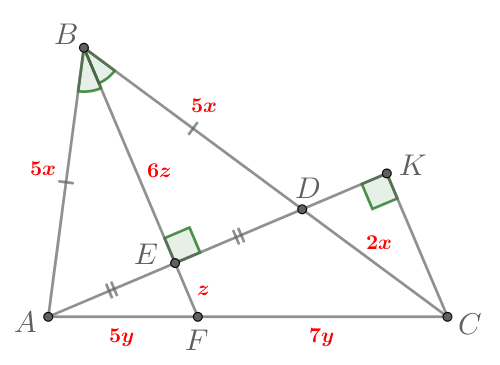
Дан треугольник $ABC,$ в котором проведены три высоты: $AA1,$ $BB1$ и $CC1.$ Через точку $C1$ проведена прямая, параллельная $BB1,$ которая пересекает $AA1$ в точке $K.$ Пусть $H$ — точка пересечения высот треугольника $ABC.$

а) Докажите, что $AB ⋅KH = BC ⋅C1H.$

б) Найдите отношение площадей треугольников $C1HK$ и $ABC,$ если $AB = 4,$ $BC = 5$ и $AC = √17.$

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

а) Рассмотрим четырехугольник $A1BC1H.$ В нем $∘ ∠BA1H = ∠BC1H = 90 ,$ значит, четырехугольник $A1BC1H$ — вписанный. Тогда внешний угол $C1HA$ при вершине $H$ равен противолежащему углу $A1BC1,$ то есть $∠C1HA = ∠A1BC1 = ∠CBA.$

Рассмотрим треугольник $ABB1.$ В нем $∠BB1A = 90∘,$ значит, по сумме углов треугольника $∠B1BA = 90∘ − ∠BAB1.$

Соответственные углы $B1BA$ и $KC1A$ образованы параллельными прямыми $BB1$ и $C1K$ и секущей $BA,$ значит, $∠B1BA = ∠KC1A.$

Рассмотрим угол $AC1H.$ Он прямой, так как $CC1$ — высота треугольника $ABC.$ Тогда

∘ ∘ ∘ ∘ ∠KC1H = 90 − ∠KC1A =90 − ∠B1BA = 90 − (90 − ∠BAB1 )= ∠BAB1 =∠BAC

Мы получили, что $∠KC1H = ∠BAC$ и $∠C1HA =∠CBA,$ значит, треугольники $ABC$ и $C1HK$ подобны по двум углам, следовательно, выполняется соотношение

AB C1H BC- = KH-- ⇒ AB ⋅KH =BC ⋅C1H

$PIC$

б) Запишем теорему косинусов для треугольника $ABC :$

AC2 = AB2 + BC2 − 2AB ⋅BC cos∠ABC ⇔

16 +25 − 17 ⇔ 17 = 16+ 25− 40 cos∠ABC ⇔ cos∠ABC = ----40---- = 0,6

Тогда мы можем найти $BC1$ и $AC1 :$

BC1 = BC cos∠ABC = 5 ⋅0,6= 3 ⇒ AC1 = AB − BC1 = 4− 3= 1

В предыдущем пункте мы доказали, что $∠CBA = ∠C1HA.$ Рассмотрим прямоугольный треугольник $C1HA.$ В нем имеем:

( ) C1H = AH cos∠C1HA = ---AC1--- cos∠C1HA = sin∠C1HA

cos∠C1HA cos∠ABC = AC1 sin∠C1HA--= AC1 sin∠ABC---

Найдем $sin∠ABC.$ Так как $∠ABC$ является углом треугольника, то $sin∠ABC > 0.$ Тогда

∘ ------------ ∘ ------- ∘ ---- sin ∠ABC = 1− cos2∠ABC = 1− 0,36= 0,64 =0,8 ⇒

0,6 3 3 ⇒ C1H = AC1 ⋅0,8-= 1⋅4 = 4

По условию $AB = 4.$ Тогда коэффициент подобия $k$ треугольников $C1HK$ и $ABC$ равен

( ) k = C1H = 34-= 3- ⇒ SC1HK-= k2 = 3- 2 =-9- AB 4 16 SABC 16 256

Ответ:

б) $-9- 256$

Ошибка.
Попробуйте повторить позже

Задача 3#30811Максимум баллов за задание: 3

На стороне $BC$ треугольника $ABC$ отмечена точка $D$ такая, что $AB = BD.$ Биссектриса $BF$ треугольника $ABC$ пересекает прямую $AD$ в точке $E.$ Из точки $C$ на прямую $AD$ опущен перпендикуляр $CK.$

a) Докажите, что $AB :BC = AE :EK.$

б) Найдите отношение площади треугольника $ABE$ к площади четырёхугольника $CDEF,$ если $BD :DC = 3:2.$

Показать ответ и решение

а) Рассмотрим треугольник $ABC.$ Так как $BF$ — его биссектриса, то по свойству биссектрисы треугольника $AB :BC = AF :FC.$

Рассмотрим треугольник $ABD.$ По условию $AB =BD,$ то есть треугольник $ABD$ равнобедренный. Поскольку $BE$ — его биссектриса, а значит, высота и медиана, то $BF ⊥ AD.$ По условию $CK ⊥AD,$ значит, $BF ∥ CK.$ Тогда по теореме о пропорциональных отрезках $AF :FC = AE :EK.$ Тогда имеем:

AB :BC = AF :FC = AE :EK

$PIC$

б) Пусть $S$ — площадь треугольника $ABE.$ Заметим, что $BE$ — медиана треугольника $ABD,$ значит, площади треугольников $ABE$ и $BDE$ равны, то есть $SABE = SBDE = S.$

По условию $BD :DC = 3:2,$ значит,

AF :FC = AB :BC = BD :BC = 3:5 ⇒ AF :AC = 3 :8

Запишем теорему Менелая для треугольника $BCF$ и секущей $AD :$

FE BD CA FE 3 8 FE 1 BE 4 EB-⋅DC- ⋅AF-= 1 ⇔ EB-⋅2 ⋅3 = 1 ⇔ EB-= 4 ⇒ BF-= 5

$PIC$

Тогда можем найти площадь треугольника $BCF :$

SBCF-= BF-⋅BC--= BF-⋅ BC = 5⋅ 5= 25 ⇒ SBCF = 25-S SBDE BE ⋅BD BE BD 4 3 12 12

Теперь мы можем найти площадь четырехугольника $CDEF :$

SCDEF = SBCF − S = 25-S− S = 13-S 12 12

Тогда искомое отношение площадей равно

SABE S 12 SCDEF-= 13S-= 13 12

Ответ:

б) $12 13$

Ошибка.
Попробуйте повторить позже

Задача 4#30812Максимум баллов за задание: 3

В параллелограмме $ABCD$ проведена биссектриса $AL$ угла $BAC.$ На прямой $CD$ за точкой $D$ отметили точку $E$ такую, что $AE = EC.$ Кроме того, $∠BAC = 2∠CAD.$

а) Докажите, что треугольники $BAC$ и $BAL$ подобны.

б) Найдите $EL,$ если $tg ∠BCA = 0,25$ и $AC = 12.$

Показать ответ и решение

а) По условию $∠BAC = 2∠CAD,$ значит, так как $AL$ — биссектриса $∠BAC,$ то

∠BAL = ∠LAC = ∠CAD

Так как $ABCD$ — параллелограмм, то $AD ∥BC.$ Следовательно, $∠CAD = ∠BCA$ как накрест лежащие углы, образованные параллельными прямыми $AD$ и $BC$ и секущей $AC.$ Тогда для внешнего угла треугольника $ALC$ имеем:

∠BLA = ∠BCA + ∠LAC = 2∠CAD

$PIC$

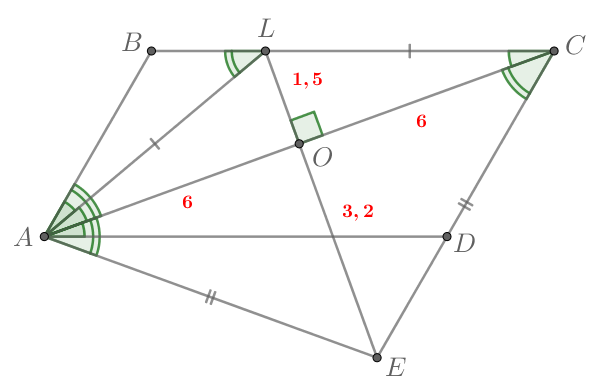
Значит, треугольники $BAC$ и $BLA$ подобны по двум углам:

∠BCA = ∠CAD = ∠BAL ∠BAC =2∠CAD = ∠BLA

б) Пусть $O$ — середина $AC,$ тогда имеем:

1 AO = CO = 2AC = 6

Рассмотрим треугольник $ALC.$ По предыдущему пункту $∠LAC = ∠LCA,$ значит, треугольник $ALC$ — равнобедренный. Следовательно, $LO ⊥ AC.$

Рассмотрим треугольник $AEC.$ По условию $AE = CE,$ значит, $EO ⊥ AC.$ Тогда точки $L,$ $O$ и $E$ лежат на одной прямой, то есть $EL =EO +OL.$

Рассмотрим треугольник $ALO.$ В нем $∠AOL = 90∘,$ значит,

OL = AO tg∠LAC = AO tg∠BCA = 6⋅0,25= 1,5

Рассмотрим треугольник $AEC.$ Так как $ABCD$ — параллелограмм, $∠ACE = ∠BAC,$ а $O$ — середина $AC,$ то в треугольнике $COE$ можем найти сторону $EO :$

EO = CO tg∠ACE =CO tg∠BAC = CO tg2∠BCA

$PIC$

По формуле тангенса двойного угла имеем:

1 tg2∠BCA = -2tg∠2BCA----= 2-⋅0,252 =-215-= 8- 1− tg ∠BCA 1− 0,25 16 15

Таким образом,

8- EO = CO tg2∠BCA =6 ⋅15 = 3,2

Тогда искомый отрезок равен

EL =EO +OL = 3,2+ 1,5= 4,7

Ответ: б) 4,7

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а),	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 5#30813Максимум баллов за задание: 3

В параллелограмме $ABCD$ на стороне $BC$ взята точка $M$ такая, что $AM = MC.$

а) Докажите, что центр окружности, вписанной в треугольник $AMD,$ лежит на диагонали $AC.$

б) Найдите радиус вписанной в треугольник $AMD$ окружности, если $AB = 5,$ $BC =10,$ $∠BAD = 60∘.$

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

а) По условию $AM = MC,$ значит, треугольник $AMC$ равнобедренный, то есть $∠MAC = ∠MCA.$

Так как $ABCD$ — параллелограмм, то $∠BCA = ∠CAD.$ Тогда $∠MAC = ∠CAD,$ следовательно, $AC$ — биссектриса угла $MAD,$ значит, центр вписанной окружности лежит на $AC.$

$PIC$

б) Обозначим $AM = MC$ через $x,$ тогда $BM = 10− x.$ По теореме косинусов в треугольнике $ABM :$

2 2 2 ∘ AM = AB + BM − 2AB ⋅BM ⋅cos120

x2 = 25+ (10− x)2 +5(10− x) ⇒ x= 7

По теореме косинусов в треугольнике $CMD$ с углом $∠MCD = 60∘ :$

MD = ∘MC2--+-CD2-− MC-⋅CD-= ∘72-+-52−-7⋅5= √39

Треугольник $AMD$ и параллелограмм $ABCD$ имеют общую высоту, равную расстоянию между прямыми $AD$ и $BC,$ и общую сторону $AD,$ перпендикулярную этой высоте. Значит, площадь $S AMD$ треугольника $AMD$ равна половине площади параллелограмма $ABCD :$

AB ⋅AD ⋅sin ∠BAD 5⋅10⋅sin 60∘ 25√3 SAMD = --------2--------= -----2-----= --2--

$PIC$

C другой стороны, площадь треугольника $AMD$ равна половине произведения его периметра на радиус вписанной окружности. Отсюда найдём радиус $r$ вписанной в треугольник $AMD$ окружности:

√- √- √ - √-- r =----2SAMD----- = ---2√5-3----= -25-3√---= 17-3−-3-13- AM + MD + AD 7+ 39+ 10 17+ 39 10

Ответ:

б) $17√3-−-3√13- 10$

Ошибка.
Попробуйте повторить позже

Задача 6#30814Максимум баллов за задание: 3

На стороне острого угла с вершиной $A$ отмечена точка $B.$ Из точки $B$ на биссектрису и на другую сторону угла опущены перпендикуляры $BC$ и $BD$ соответственно.

a) Докажите, что $AC2 +CD2 =AD2 + BD2.$

б) Прямые $AC$ и $BD$ пересекаются в точке $T.$ Найдите отношение $AT :TC,$ если $cos∠ABC = 3. 8$

Источники: ЕГЭ 2022, основная волна

Показать ответ и решение

a) Углы $BCA$ и $BDA$ прямые, значит, точки $C$ и $D$ лежат на окружности с диаметром $AB.$

Биссектриса $AC$ вписанного угла $BAD$ делит дугу $BCD$ пополам, значит, хорды $BC$ и $CD,$ стягивающие равные дуги, равны. Отсюда с учетом теоремы Пифагора для треугольников $ABC$ и $ABD :$

AC2 + CD2 = AC2 + BC2 =AB2 = AD2 + BD2

$PIC$

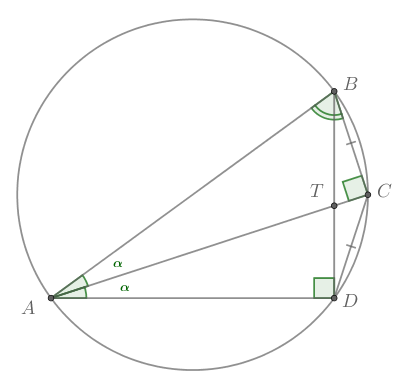
б) Пусть $∠BAC = ∠CAD = α,$ тогда из прямоугольного треугольника $ABC :$

3 sinα = sin∠BAC = cos∠ABC = 8

Вписанные углы, опирающиеся на одну дугу, равны, тогда

∠CBD = ∠CAD = α ⇒ TC = BC ⋅tgα

В прямоугольных треугольниках $ABC,$ $ABD$ и $AT D :$

AB = BC-; AD = AB ⋅cos2α= BC--⋅cos2α; AT = -AD- = BC-⋅cos2α- sinα sinα cosα sinα ⋅cosα

Тогда искомое отношение равно

( ) BC-⋅cos2α cos2α- 1−-2sin2α 1−-2⋅-38-2 46 AT :TC = sin α⋅cosα :(BC ⋅tgα) = sin2α = sin2 α = (38)2 = 9

Ответ:

б) $46 9$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#105258Максимум баллов за задание: 3

а) Докажите, что $AL ⋅BC = AB ⋅AC$ .

б) Найдите $EL,$ если $tg ∠BCA = 0,5$ и $AC = 8.$

Показать ответ и решение

а) По условию $∠BAC = 2∠CAD,$ значит, так как $AL$ — биссектриса $∠BAC,$ то

∠BAL = ∠LAC = ∠CAD

∠BLA = ∠BCA + ∠LAC = 2∠CAD

$PIC$

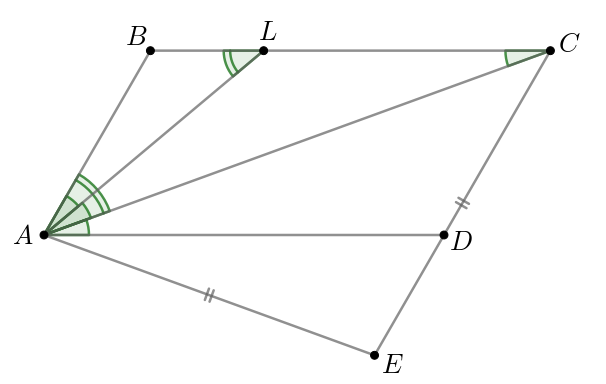
Значит, треугольники $BAC$ и $BLA$ подобны по двум углам:

∠BCA = ∠CAD = ∠BAL ∠BAC =2∠CAD = ∠BLA

Запишем соотношение сторон этих треугольников:

AL AB AC- = BC- AL ⋅BC = AB ⋅AC

б) Пусть $O$ — середина $AC,$ тогда имеем:

1 AO = CO = 2AC = 4

Рассмотрим треугольник $ALO.$ В нем $∠AOL = 90∘,$ значит,

OL = AO tg ∠LAC = AO tg∠BCA = 4⋅0,5 =2

EO = CO tg∠ACE =CO tg∠BAC = CO tg2∠BCA

$PIC$

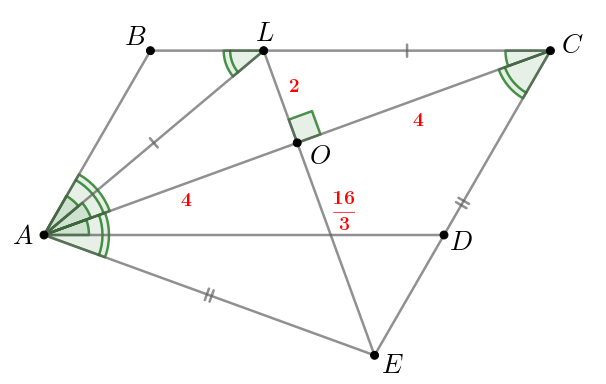
По формуле тангенса двойного угла имеем:

tg2∠BCA = -2tg∠B2CA----= -2⋅0,52-= 13-= 4 1− tg ∠BCA 1− 0,5 4 3

Таким образом,

4 16 EO = CO tg2∠BCA = 4⋅3 = 3

Тогда искомый отрезок равен

16 22 EL = EO + OL = 2+ -3 = 3-

Ответ:

б) $22 3$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а),	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 8#106604Максимум баллов за задание: 3

a) Докажите, что $AB :BC = AE :EK.$

б) Найдите отношение площади треугольника $ABE$ к площади четырёхугольника $CDEF,$ если $BD :DC = 5:2.$

Показать ответ и решение

$PIC$

Рассмотрим треугольник $ABD.$ По условию $AB =BD,$ то есть треугольник $ABD$ равнобедренный. Поскольку $BE$ — его биссектриса, а значит высота и медиана, то $BF ⊥AD.$ По условию $CK ⊥ AD,$ значит, $BF ∥CK.$ Тогда по теореме о пропорциональных отрезках $AF :FC = AE :EK.$ Тогда имеем:

AB :BC = AF :FC = AE :EK.

По условию $BD :DC = 5:2,$ значит,

AF AB BD 5 F-C = BC-= BC-= 7,

следовательно,

AF-= -5. AC 12

Запишем теорему Менелая для треугольника $BCF$ и секущей $AD :$

FE BD CA EB-⋅-DC ⋅AF- =1 F E 5 12 EB- ⋅2 ⋅ 5-= 1 F-E = 1 EB 6

Значит,

BE- = 6. BF 7

$PIC$

Тогда можем найти площадь треугольника $BCF :$

SBCF BF ⋅BC BF BC 7 7 49 SBDE-= BE-⋅BD--= BE-⋅BD- = 6 ⋅ 5 = 30,

следовательно,

SBCF = 49S. 30

Теперь мы можем найти площадь четырехугольника $CDEF :$

SCDEF = SBCF − S = 49S − S = 19S. 30 30

Тогда искомое отношение площадей равно

-SABE- -S-- 30- SCDEF = 1390S = 19 .

Ответ:

б) $30 19$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а),	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 9#26923Максимум баллов за задание: 3

На сторонах $AB$ и $BC$ треугольника $ABC$ отмечены точки $M$ и $N$ так, что $AM :MB = CN :NB = 1:2.$ Вписанная окружность треугольника $ABC$ касается отрезка $MN$ в точке $L.$

а) Докажите что $AB + BC = 5AC.$

б) Известно, что $ML = 1,$ $LN = 3.$ Найдите радиус вписанной окружности.

Источники: ЕГЭ 2022, досрочная волна

Показать ответ и решение

а)

$PIC$

Из условия известно, что

AM :MB = 1:2 ⇒ MB = 2AM ⇒ AB = AM + MB = AM + 2AM = 3AM

Аналогично,

CN :NB = 1:2 ⇒ NB =2CN ⇒ CB = CN + NB = CN + 2CN =3CN

Тогда

AB + BC = 3AM +3CN =3(AM +CN )

Рассмотрим треугольники $ABC$ и $MBN$ . В них

∠ABC = ∠MBN, -AB- = 3AM--= 3 = 3CN- = CB-- MB 2AM 2 2CN NB

Тогда треугольники $ABC$ и $MBN$ подобны, при этом

AB--= CB--= AC--= 3 ⇒ 3MN = 2AC MB NB MN 2

Рассмотрим четырехугольник $AMNC$ . Он описан около окружности, т.е. суммы длин его противоположных сторон равны:

CN + AM = AC +NM ⇒ AB + BC = 3(AM + CN )= 3(AC + NM )= 3AC + 3MN

Мы уже доказали, что $3MN = 2AC$ , откуда получаем, что

AB + BC = 3AC +3MN = 3AC + 2AC = 5AC

Что и требовалось доказать.

б)

$PIC$

Обозначим $AM = x, CN = y$ . Так как $ML =1$ , $LN = 3$ , имеем:

MN = ML + NL = 1+ 3= 4

В пункте а) было доказано, что $3MN = 2AC$ , откуда следует, что

AC = 3MN = 3 ⋅4= 6 2 2

Тогда, так как четырехугольник $AMNC$ — описанный,

AM + CN = AC + MN ⇔ x+ y = 6 +4 = 10

$AB$ — касательная к окружности, вписанной в треугольник $ABC$ . Обозначим её точку касания с окружностью за $P$ . $CB$ — касательная к окружности, вписанной в треугольник $ABC$ . Обозначим её точку касания за $T$ . Тогда $BP = BT$ по свойству касательных.

Также по свойству касательных $MP = ML$ и $NT = NL$ . Тогда

BP = BT ⇔ BM + MP = BN + NT ⇔ BM +ML = BN + NL

Известно, что $ML = 1$ , $LN =3$ . Также $BM = 2AM = 2x$ , $BN = 2CN = 2y$ . Подставив эти значения, получим, что

2x+ 1= 2y+ 3 ⇔ 2x = 2y + 2 ⇔ x= y+ 1

Подставив такое значение $x$ в формулу $x+ y = 10$ , получим

9 9 11 (y +1)+ y =10 ⇔ 2y = 9 ⇔ y = 2 ⇒ x= y+ 1 = 2 + 1=-2

Получили, что $AM = 112 , CN = 92$ . Тогда

AB = 3AM =3 ⋅ 11= 33, CB = 3CN = 3⋅ 9 = 27 2 2 2 2

Таким образом, мы нашли все стороны треугольника $ABC$ . Тогда его полупериметр равен

( ) ( ) p= 1(AB + BC + AC )= 1 33+ 27 +6 = 1 60+ 6 = 36= 18 2 2 2 2 2 2 2

Найдем теперь его площадь по формуле Герона:

∘ ---(------)--(------)-------- ∘----------- S = ∘p(p−-AB-)(p-− BC-)(p-− AC-)= 18⋅ 18− 33 ⋅ 18− 27 (18− 6)= 18⋅ 3⋅ 9 ⋅12 = 27√2 2 2 2 2

Из формулы площади через радиус вписанной окружности выразим радиус:

S 27√2 3√2 S =pr ⇔ r = p-= -18--= -2--

Ответ:

б) $3√2- 2$

Ошибка.
Попробуйте повторить позже

Задача 10#26924Максимум баллов за задание: 3

Точка $M$ — середина стороны $AB$ треугольника $ABC.$ В треугольник вписана окружность, которая касается $AB$ в точке $P.$

а) Докажите, что $PM = 12|AC − BC |.$

б) Известно, что $BC > AC$ и $AM =MC,$ а $P M$ относится к радиусу вписанной окружности как 7 к 4. Найдите углы треугольника.

Источники: ЕГЭ 2022, досрочная волна

Показать ответ и решение

а) Докажем лемму.

Длина касательной из вершины треугольника к его вписанной окружности равна разности полупериметра и противоположной стороны. В частности, $AB1 = AC1 = p− BC$ .

Рассмотрим произвольный треугольник $ABC$ . Пусть его вписанная окружность касается сторон $AB$ , $BC$ и $AC$ в точках $C1$ , $A1$ и $B1$ соответственно. Тогда найдем длину отрезка касательной $AB1$ к вписанной окружности. Мы знаем, что отрезки касательных с окружности, проведенных из одной точки, равны. Поэтому $AB1 = AC1$ , $BA1 = BC1$ и $CA1 = CB1$ .

$PIC$

Тогда можем составить систему:

( ||| AB = AB1 + BC1 ( { { AB1 = AB+AC−B2C1−CA1- AB-+-AC-−-BC- ||| BC = BC1 + CA1 ⇒ ( BC = BC1 + CA1 ⇒ AB1 = 2 = p− BC ( AC = AB1 +CA1

__________________________________________________________________________________________________

Вернемся к задаче. По доказанной лемме $AP = 1 (AB + AC − BC ) 2$ . Тогда если $BC > AC$ , отрезок $AP$ меньше половины $AB$ , и точка $P$ лежит между точками $A$ и $M$ . Значит,

1 1 1 PM = AM − AP = 2AB − 2 (AB + AC − BC )= 2 (BC − AC)

Если $BC < AC$ , то отрезок $AP$ больше половины $AB$ , и точка $M$ лежит между точками $A$ и $P$ . Значит,

PM = AP − AM = 1 (AB +AC − BC )− 1AB = 1 (AC − BC ) 2 2 2

Если $AC =BC$ , то точки $P$ и $M$ совпадают, следовательно,

PM = 1(AC − BC) =0 2

В любом случае мы получили, что

1 PM = 2|AC − BC |

б) Рассмотрим треугольник $ABC$ . По условию $M$ — середина стороны $AB$ . Тогда $AM = BM = CM$ , значит, треугольник $ABC$ прямоугольный, то есть $∠C = 90∘$ .

Пусть $Q$ и $R$ — точки касания вписанной окружности треугольника $ABC$ и его сторон $AC$ и $BC$ соответственно. Отрезки касательных, проведенных к окружности из одной точки равны, значит, $AQ = AP$ , $BP = BR$ и $CQ = CR$ .

Пусть $I$ — центр вписанной окружности, тогда $IQ ⊥AC$ и $IR ⊥ BC$ . Рассмотрим четырехугольник $IQCR$ . Его углы $IQC$ , $QCR$ и $CRI$ равны $90∘$ , значит, $IQCR$ — прямоугольник. $CQ = CR$ , следовательно, $IQCR$ — квадрат. Значит, $CQ =CR =r$ , где $r$ — радиус вписанной окружности $△ ABC$ .

$PIC$

По условию $BC > AC$ , значит, точка $P$ лежит между точками $A$ и $M$ . Тогда $AB = AP + PM + BM$ . По условию $P M = 74r$ . Пусть $AP = AQ = x$ . Заметим, что

BR = BP ⇔ BR = P M + BM ⇔ BR = P M + AM ⇔ BR = AP + 2PM ⇔ BR = x+ 7r 2

Тогда в треугольнике $ABC$ стороны равны $7 AB = AP + BP = 2x+ 2r$ , $AC = x +r$ и $9 BC = x+ 2r$ . Запишем теорему Пифагора:

AB2 = AC2 +BC2 ⇔ 4x2+ 14xr+ 49r2 = x2+ 2xr+ r2+ x2+ 9xr+ 81r2 ⇔ 2x2+3xr − 9r2 = 0 4 4

Решим полученное квадратное уравнение относительно $x$ :

−3r± √9r2-+72r2- −3r± 9r 3 x = -------4------- = ---4--- ⇒r>0 x = 2r

Тогда $AC = 52r$ и $BC = 6r$ , значит,

∠A =arctg BC-= arctg -6r--= arctg 12 ⇒ ∠B =90∘− arctg 12- AC 2,5r 5 5

Ответ:

б) $∘ 12 ∘ 12 ∠C =90 ,∠A = arctg 5 ,∠B = 90 − arctg 5$

Ошибка.
Попробуйте повторить позже

Задача 11#26926Максимум баллов за задание: 3

Прямая, параллельная боковой стороне $CD$ равнобокой трапеции $ABCD,$ пересекает боковую сторону $AB$ в точке $F$ и основание $AD$ в точке $E.$ Оказалось, что $F C = ED.$

а) Докажите, что углы $AF E$ и $BCF$ равны.

б) Известно, что $FE = 5,$ $ED :F B = 3:1,$ а площадь четырехугольника $FCDE$ равна $14√35.$ Найдите площадь трапеции $ABCD.$

Источники: ЕГЭ 2022, досрочная волна

Показать ответ и решение

а) Обозначим $∠BAD = α.$ В равнобедренной трапеции $ABCD$ имеем:

∘ ∠BAD = ∠CDA = α, ∠ABC = ∠BCD = 180 − α

Так как $FE ∥ CD,$ то четырехугольник $FCDE$ — трапеция. По условию $F C = ED,$ значит, трапеция является равнобедренной. Тогда, так как $∠CDE = α,$ то

∠F CD = ∠CDE = α, ∠CF E =∠DEF = 180∘− α

Тогда

∠BCF = ∠BCD − ∠F CD = (180∘ − α )− α = 180∘− 2α

$PIC$

Также

∠AEF = 180∘ − ∠F ED = 180∘− (180∘− α)= α

Тогда по сумме углов треугольника $AFE$

∠AF E = 180∘ − ∠F AE − ∠FEA = 180∘− α − α = 180∘− 2α = ∠BCF

Что и требовалось доказать.

б) Мы в предыдущем пункте доказали, что $∠F EA = ∠FAE,$ значит, треугольник $AF E$ — равнобедренный. Тогда

AF = FE = 5

Пусть $BF =x.$ Тогда, так как по условию $ED :F B =3 :1,$ то $ED =3x.$ Но трапеция $F CDE$ равнобедренная, поэтому и $F C = 3x.$

Трапеция $ABCD$ — равнобедренная, поэтому

CD = AB = AF + BF = 5 +x

$PIC$

Теперь, заметим, что если мы найдем $x,$ то сможем найти все стороны трапеции $ABCD$ и вычислить ее площадь. Значит, нужно найти $x.$

В равнобедренной трапеции $FCDE$ мы смогли выразить все стороны через $x.$ По условию нам дана ее площадь. Заметим, что равнобедренная трапеция является вписанным четырехугольником, следовательно, мы можем найти ее площадь с помощью формулы Брахмагупты:

∘ ---------------------- S = (p − a)(p− b)(p − c)(p− d),

где $a,$ $b,$ $c$ и $d$ — стороны четырехугольника, а $p$ — его полупериметр.

Найдем полупериметр трапеции $FCDE :$

3x+ (5 +x) +3x +5 7x p = -------2---------= 2-+ 5

Тогда

∘ (----------)(------------)-(----------)(---------)- SFCDE = 7x-+ 5− 3x 7x+ 5− x − 5 7x + 5− 3x 7x+ 5− 5 = 2 2 2 2 ∘---------------------- ∘ ------------- √ -- = ( x+ 5)⋅ 5x ⋅(x +5) ⋅ 7x= (x + 5)2⋅ 35x2= (x + 5)⋅ x-35 2 2 2 2 2 4 2 2

Так как по условию $√--- SFCDE = 14 35,$ то имеем уравнение на $x >0 :$

√ -- (x ) x--35 √-- -4-- 2 + 5 ⋅ 2 = 14 35 |⋅√35 (x2+ 10)⋅x = 14⋅4 x + 10x− 56= 0 (x + 14)(x− 4)= 0 x =4

Итак, мы нашли $x= 4.$ Теперь найдем $cosα.$ Опустим перпендикуляр $EH$ из точки $E$ на сторону $CD.$ Из прямоугольного треугольника $EDH$ имеем:

cosα= DH--= -x2 = 2-= 1 ED 3x 12 6

Тогда посмотрим, что мы имеем в трапеции $ABCD.$ Мы знаем, что ее боковые стороны $AB$ и $CD$ равны 9, а

cos∠BAD = cosα = 1 6

Найдем ее сторону $AD.$ Мы знаем, что

AD =AE + ED =AE +12

Заметим, что $AE$ — основание равнобедренного треугольника, тогда

10 5 AE = 2AF ⋅cos∠F AE = 2⋅5 ⋅cosα = 6 = 3

Таким образом,

AD = 5 + 12 = 5+-36= 41 3 3 3

Значит, так как $ABCD$ — равнобедренная трапеция, то

41 41 18 41− 9 32 BC = AD − 2AB ⋅cos∠BAD = -3 − 2⋅9⋅cosα = -3 − 6-= --3-- = 3-

$PIC$

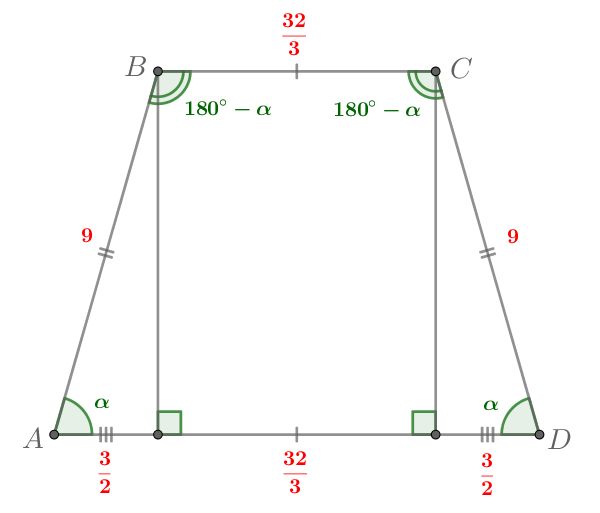
Вычислим полупериметр трапеции $ABCD :$

1 ( 32 41-) 73 2 9+ 3 + 9 + 3 = 6 + 9

Тогда по формуле Брахмагупты

∘ (---------)(----------)-(---------)(----------)- S = 73+ 9− 9 73+ 9− 32 73 + 9− 9 73+ 9− 41 = ABCD 6 6 3 6 6 3 ∘---------------------------------- 73 (73 − 64+ 54) 73 ( 73− 82+ 54 ) 73 ∘ 63⋅45- 73 3√35 73√35 = 6-⋅ -----6---- ⋅6-⋅ ----6----- = -6 ⋅ -36--= -6 ⋅-2---= --4--

Ответ:

б) $73√35- 4$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#30833Максимум баллов за задание: 3

Дан равнобедренный треугольник $ABC,$ в котором $AB = BC.$ На стороне $AC$ взяли точку $D,$ а также отметили центры $I$ и $J$ описанных окружностей треугольников $ABD$ и $CBD$ соответственно.

а) Докажите, что $BI ∥DJ.$

б) Найдите $IJ,$ если $AC =12$ и $3 cos∠BDC = 7.$

Источники: ЕГЭ 2022, резервная волна

Показать ответ и решение

а) Сравним радиусы описанных окружностей треугольников $ABD$ и $CBD$ . Рассмотрим треугольник $ABD$ . По теореме синусов найдем радиус его описанной окружности:

AB AB sin-∠BDA-= 2RABD ⇒ RABD = 2sin-∠BDA-

По теореме синусов найдем радиус описанной окружности треугольника $CBD$ :

BC BC sin-∠BDC-= 2RCBD ⇒ RCBD = 2sin-∠BDC-

Углы $BDA$ и $BDC$ — смежные, значит,

∠BDA + ∠BDC = 180∘ ⇒ sin∠BDA = sin∠BDC

Треугольник $ABC$ — равнобедренный ( $AB = BC$ ), значит,

AB AB BC RABD = 2sin-∠BDA-= 2sin-∠BDC-= 2sin-∠BDC-= RCBD

$PIC$

Рассмотрим четырехугольник $IBJD$ . В нем $BI =DI = RABD$ и $BJ = DJ =RCBD$ , значит, $IBJD$ — ромб. Тогда его противоположные стороны параллельны, то есть $BI ∥DJ$ .

б) Пусть $M$ — середина $AD$ , $N$ — середина $CD$ . Точки $I$ и $J$ — центры описанных окружностей, значит, $IM$ и $JN$ — серединные перпендикуляры к $AD$ и $CD$ соответственно. Также точки $I$ и $J$ лежат на серединном перпендикуляре к $BD$ , значит, $IJ ⊥BD$ .

Пусть $K$ — середина $BD$ . Рассмотрим четырехугольник $IKDM$ . В нем $∘ ∠IKD =90$ , так как $IJ ⊥ BD$ , и $∘ ∠IMD = 90$ , так как $IM ⊥ AC$ . Значит, $IKDM$ — вписанный. Тогда

∘ ∘ ∘ ∘ ∠KIM + ∠BDA =180 ⇒ ∠BDC =180 − ∠BDA = 180 − (180 − ∠KIM )= ∠KIM

По условию $cos∠BDC = 3 7$ , значит, $0∘ < ∠BDC < 90∘$ . Опустим из точки $J$ перпендикуляр $JH$ на $IM$ . Рассмотрим треугольник $IJH$ . В этом треугольнике