№14 из ЕГЭ 2016
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде сторона
основания равна
а высота
пирамиды равна 3. Точки
и
— середины ребер
и
соответственно. Отрезок
— высота пирамиды
с вершиной
и основанием
а) Докажите, что точка является серединой отрезка
б) Найдите расстояние между прямыми и
Источники:
а) Так как пирамида правильная, то и
следовательно, перпендикуляр из точки
на плоскость
упадет на прямую
Таким образом, точка
лежит на прямой
По теореме Пифагора следовательно
— правильный. Тогда, так как
является его высотой, то
также является медианой, следовательно,
— середина
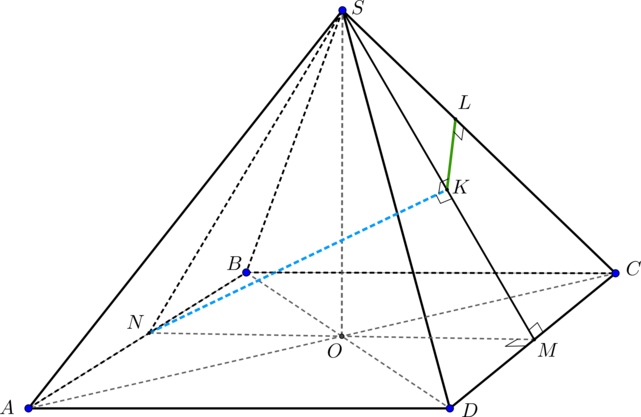
б) Прямые и
скрещиваются, следовательно, расстояние между ними — это длина их общего перпендикуляра.
Проведем Тогда
— искомое расстояние между
и
так как
а значит
Рассмотрим По теореме Пифагора
Запишем отношение подобия треугольников и
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной призме сторона
основания равна 6, а боковое ребро
равно
На
ребрах
и
отмечены точки
и
соответственно, причем
Плоскость
параллельна прямой
и содержит прямую
а) Докажите, что прямая перпендикулярна плоскости
б) Найдите расстояние от точки до плоскости
Источники:
а) Построим сечение призмы плоскостью Так как
то
пересечет плоскости
и
по прямым,
параллельным прямой
Если линия пересечения
и
не параллельна
то прямая
будет пересекать
следовательно, не может быть ей параллельна.
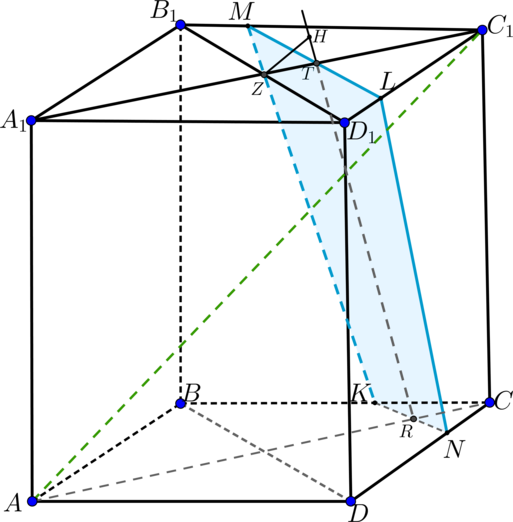
Проведем и
Таким образом,
— сечение призмы плоскостью
По теореме о трех перпендикулярах как наклонная, так как
Рассмотрим сечение призмы плоскостью
Докажем, что
Отсюда будет следовать, что
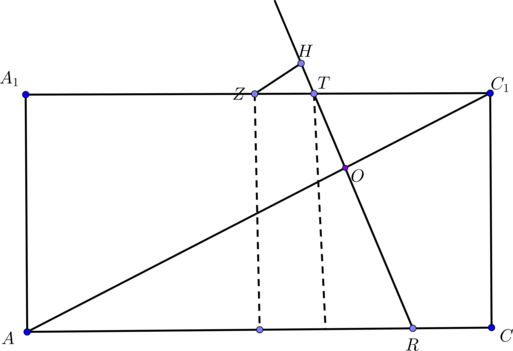
Таким образом, нужно доказать, что треугольник — прямоугольный. По теореме Пифагора
Из подобия треугольников и
Аналогично Тогда по теореме Пифагора
Далее имеем с коэффициентом 2. Следовательно,
По обратной теореме Пифагора
получаем
б) Так как прямая то расстояние от любой точки прямой
до плоскости
будет одинаковым.
Следовательно,
Проведем Так как
и
то
Так как прямая
принадлежит плоскости
то
Тогда
и
следовательно
Найдем Так как
то

б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде сторона основания
равна 16, а высота равна 4. На ребрах
отмечены точки
и
соответственно, причем
а) Докажите, что плоскости и
параллельны.
б) Найдите расстояние от точки до плоскости
Источники:
а) Построим плоскость Так как
то
Так как
и
то линия пересечения плоскостей
и
тоже будет параллельна
Значит, проведем Трапеция
— искомое сечение.
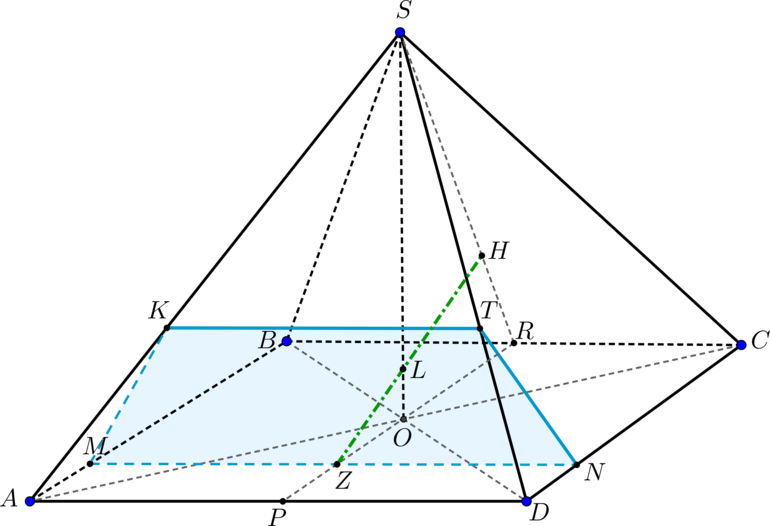
Для того, чтобы две плоскости были параллельны друг другу, необходимо и достаточно, чтобы две пересекающиеся прямые из
одной плоскости были параллельны двум пересекающимся прямым из другой плоскости. Уже известно, что Нужно
найти еще одну пару параллельных прямых. Докажем, что
Пусть — высота пирамиды. Тогда по теореме Пифагора в треугольниках
и
имеем:
Заметим, что
Следовательно, значит,
Таким образом, мы доказали, что плоскости и
параллельны.
б) Так как плоскости и
параллельны, то расстояние от любой точки одной из плоскостей до другой плоскости
фиксировано. Таким образом, неважно, из какой точки плоскости
опускать перпендикуляр на плоскость
Проведем через точку прямую
Опустим перпендикуляр
из точки
Так как
то точка
будет лежать на прямой

Рассмотрим сечение Проведем
Тогда
следовательно,
В выразим высоту из вершину прямого угла через гипотенузу и катеты:
Значит,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме сторона основания
равна 12, а боковое ребро
равно 6. На ребре
отмечена точка
так, что
Точки
— середины ребер
и
соответственно. Плоскость
параллельна
прямой
и содержит точки
и
а) Докажите, что прямая перпендикулярна плоскости
б) Найдите объем пирамиды, вершина которой – точка а основание — сечение данной призмы плоскостью
Источники:
а)
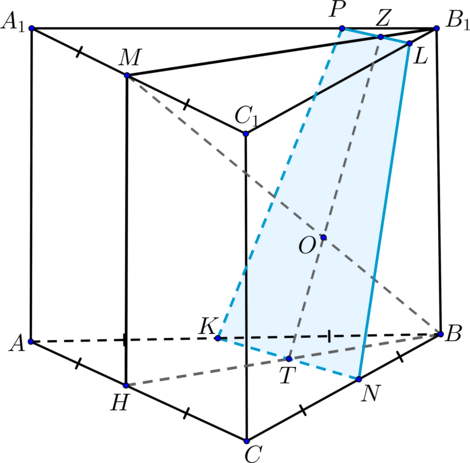
Построим сечение пирамиды плоскостью Т.к. плоскость
параллельна прямой
, то она будет пересекать основания
призмы по прямым, параллельным прямой
. Следовательно, прямая пересечения плоскости
с плоскостью
– прямая
, прямая пересечения плоскости
с плоскостью
– прямая
. Таким образом, сечение призмы
плоскостью
– равнобокая трапеция
.
Для того, чтобы прямая была перпендикулярна плоскости, она должна быть перпендикулярна двум пересекающимся прямым из
этой плоскости.
Проведем по теореме о трех перпендикулярах
(наклонная)
, т.к.
(проекция)
.

пересекает плоскость
на прямой
, где
– середины
и
соответственно. Докажем, что
.
Для этого покажем, что
.
Рассмотрим сечение .
– высота правильного треугольника
со стороной 12, следовательно,
– высота правильного треугольника
со стороной 2, следовательно,
.
Таким образом, .
Следовательно, подобен
по двум углам
.
Таким образом, и
.
б) Найдем – высоту пирамиды
.
Так как , то
Аналогично, .
Найдем высоту трапеции
.
Из прямоугольного по теореме Пифагора
Кроме того, . Значит:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме все рёбра равны 8. На рёбрах
и
отмечены точки
и
соответственно, причём
а) Докажите, что плоскость разбивает призму на два многогранника, объёмы которых равны.
б) Найдите объём тетраэдра
Источники:
а) Плоскость делит призму на два многогранника —
и
. В условии нас просят сравнить их
объёмы. Для этого сначала вычислим объём всей призмы. Так как
— правильная призма, то её объём вычисляется
по формуле
![]()
Тогда найдем объём многогранника — пирамиды с основанием
и вершиной
. Пусть
—
высота правильного треугольника
. Тогда, так как
является правильной призмой, высота
. Следовательно, объём пирамиды
равен
— высота правильного треугольника
со стороной 8, значит,
. Найдем площадь основания
. Заметим, что
, так как это боковые ребра правильной призмы. По условию
и
,
тогда
значит, мы можем найти площадь трапеции :
Тогда теперь мы можем найти объёмы многогранников и
:
Значит, объёмы многогранников и
равны.
б) Заметим, что
![]()
Аналогично предыдущему пункту мы можем найти объём пирамиды :
— высота правильного треугольника
со стороной 8, тогда
. Найдем площадь основания
.
Заметим, что
, так как это боковые ребра правильной призмы. По условию
и
, тогда площадь
трапеции
равна
Теперь найдём объём пирамиды :
Следовательно, объём тетраэдра равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная призма все рёбра которой равны 6. Через точки
и середину
ребра
проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью
Источники:
а) Так как — правильная треугольная призма, то рёбра
и
перпендикулярны плоскостям, в
которых лежат основания
и
Также известно, что все ребра призмы равны, тогда грани
и
— квадраты со стороной 6.
Найдём длину отрезка Он является гипотенузой в треугольнике
значит, по теореме Пифагора
Треугольник является прямоугольным, значит, по теореме Пифагора
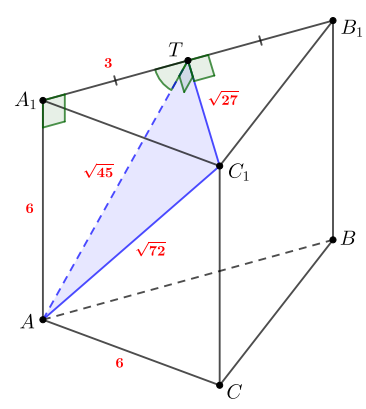
Отрезок является медианой и высотой правильного треугольника
со стороной 6, значит,
Заметим, что
Значит, по теореме, обратной теореме Пифагора, является прямоугольным, причём
б) Угол между плоскостями и
равен углу между плоскостями
и
так как
Плоскости
и
пересекаются по прямой
Заметим, что прямая перпендикулярна
как медиана в равностороннем треугольнике
С другой стороны,
по предыдущему пункту.

Тогда угол между плоскостями и
равен углу между прямыми
и
(очевидно, что этот угол
меньше прямого).
Рассмотрим треугольник В нём имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме сторона основания
равна 6, а боковое ребро
равно
На ребрах
и
отмечены токи
и
соответственно, причем
а) Пусть — точка пересечения плоскости
с ребром
Докажите, что
— квадрат.
б) Найдите площадь сечения призмы плоскостью
Источники:
а) Рассмотрим четырехугольник . Т.к. плоскости основания параллельны, то линии пересечения этих плоскостей с
плоскостью
тоже параллельны, то есть
.
Заметим, что если совместить наложением равные равносторонние треугольники и
так, чтобы точка
наложилась на
, точка
на
, то точка
наложится на
(из-за параллельности
и
).
Следовательно, . Следовательно,
. Таким образом, по признаку
– параллелограмм.
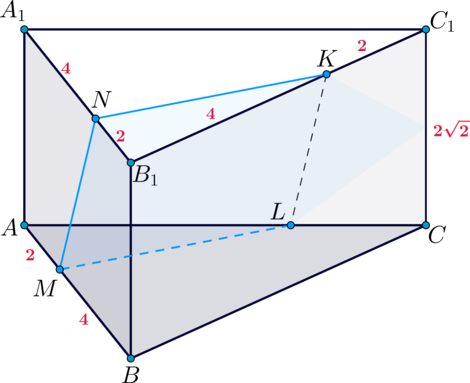
Как следствие, .
По теореме косинусов из найдем
Заметим, что (
), следовательно, по обратной теореме Пифагора
.
Таким образом, и
, следовательно,
, следовательно,
.
Таким образом, и
– параллелограмм, у которого один угол прямой, следовательно, все углы прямые,
следовательно, это прямоугольник.
Для того, чтобы доказать, что это квадрат, достаточно доказать равенство двух смежных сторон. Поэтому покажем, что
.
Рассмотрим грань и проведем в ней
, чтобы найти
.
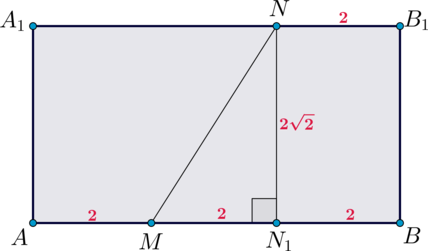
Тогда , следовательно,
. Тогда из прямоугольного
имеем:
Таким образом, , чтд.
б) Построим сечение призмы плоскостью . Для этого необходимо найти отрезки, по которым она пересекает грани
и
.
Пусть – точка пересечения прямых
и
. Тогда
лежит в грани
. Следовательно, соединив
точки
и
, получим точку пересечения плоскости с ребром
– точку
. Тогда
– искомое
сечение.
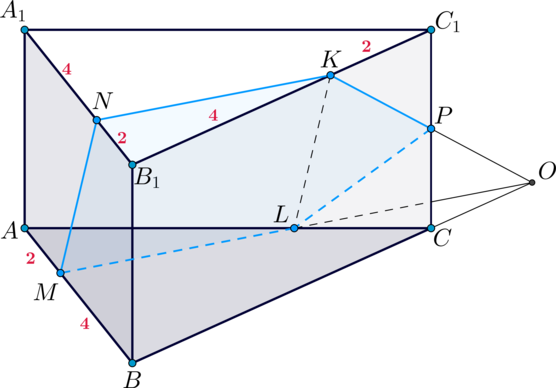
Его площадь будем искать как сумму площади квадрата и треугольника
.
Площадь квадрата равна
.
По теореме Менелая для и прямой
имеем:
Таким образом, как прямоугольные по катету и острому углу, следовательно,
.
Тогда по теореме Пифагора:
То есть равнобедренный. Следовательно, его высота
из вершины
к основанию (на рисунке не отмечена) по
теореме Пифагора ищется как
Тогда
Следовательно, площадь сечения равна .
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На ребрах и
куба
с ребром 12 отмечены точки
и
соответственно, причем
Плоскость
пересекает ребро
в точке
а) Докажите, что точка делит ребро
пополам.
б) Найдите расстояние от точки до плоскости
Источники:
а) Так как грани и
параллельны, то плоскость
пересечет их по параллельным прямым. Поэтому
.
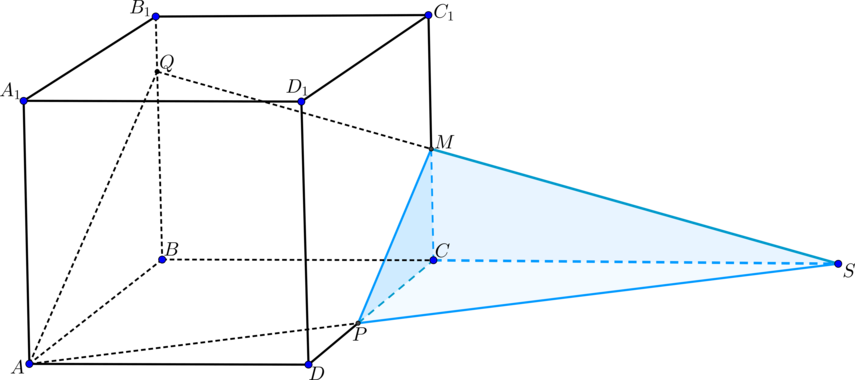
Таким образом, , т.е.
– середина ребра
.
б) Расстояние от точки до плоскости
равно высоте
пирамиды
(
– ее вершина,
– основание).
Найдем
с помощью формулы:
Для этого рассмотрим эту пирамиду как пирамиду с вершиной в точке .
. Из подобия
треугольников
и
найдем
. Следовательно,
.
По теореме Пифагора .
Тогда по формуле Герона
Следовательно,
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме сторона
основания равна 12, а высота призмы равна 2. На ребрах
и
отмечены точки
и
соответственно, причем
Плоскость
пересекает ребро
в точке
а) Докажите, что точка является серединой ребра
б) Найдите расстояние от точки до плоскости
Источники:
а) Обозначим Так как плоскости
и
параллельны, то плоскость
пересечет их по параллельным
прямым, то есть
Тогда
откуда имеем:
Следовательно,
Тогда точка делит ребро
пополам и является его серединой.
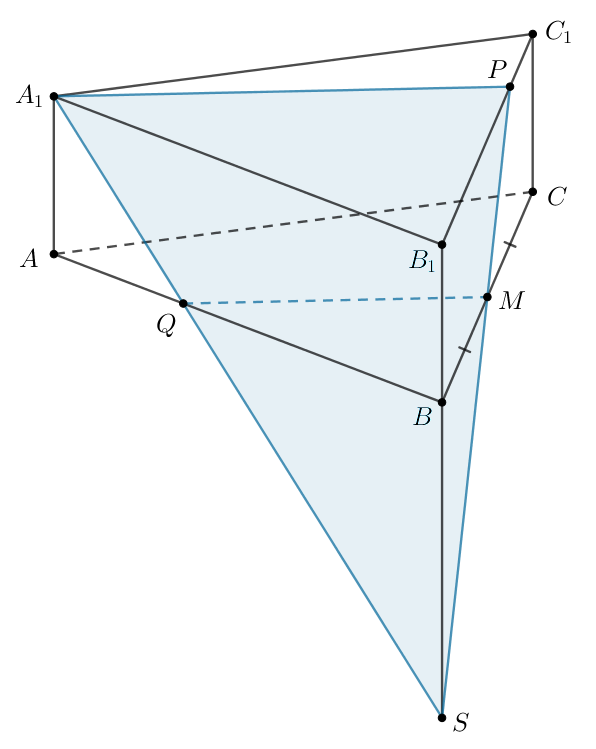
б) Расстояние от точки до плоскости
равно высоте пирамиды
проведенной из вершины
к основанию
Рассмотрим как пирамиду с вершиной в точке
и основанием
Тогда
Из подобия треугольников и
найдем
Тогда
По теореме Пифагора в треугольнике найдем
По теореме Пифагора в треугольнике найдем
По теореме косинусов в треугольнике найдем
Следовательно, и
— равнобедренный. С помощью высоты, проведенной к основанию
найдем
Тогда искомое расстояние равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |


