backlog (работа над имеющимися решениями)
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Докажем утверждение для вписанной окружности. Для вневписанных рассуждения аналогичны. Пусть — длина
отрезка
точка касания вписанной со стороной
и середина стороны
соответственно. Аналогично определим
![]()
Отрезки и
равны
где
— полупериметр треугольника
Без ограничений общности, можем считать, что
следовательно,
Тогда, по обратной слабой теоремы Кэзи, касание эквивалетно выполнению соотношения
которое верно при любых после приведения общих слагаемых.
Ошибка.
Попробуйте повторить позже
Хорды и
окружности
пересекаются в точке
Докажите, что радикальная ось окружностей, вписанных в криволинейные
треугольники
и
проходит через середины дуг
и
Пусть — окружности вписанные в криволинейные треугольники
соответственно,
— середина меньшей дуги
окружности
— точки касания
c прямыми
и
соответственно. Достаточно доказать, что длины касательных из точки
до окружностей
и
равны.
![]()
Найдем длину касательной из к
(обозначим её длину за
). По теореме Кэзи для
,
,
,
имеем
а поскольку
Аналогично, длина касательной из к окружности
будет равна тому же, что завершает доказательство.
Ошибка.
Попробуйте повторить позже
Окружности касаются внешним образом в точке
, а также обе касаются внутренним образом некоторой окружности
Внешняя
касательная к
и
пересекает
в точках
и
а общая касательная в точке
— в точке
по ту же сторону от
что и
Докажите, что
— центр вписанной окружности треугольника
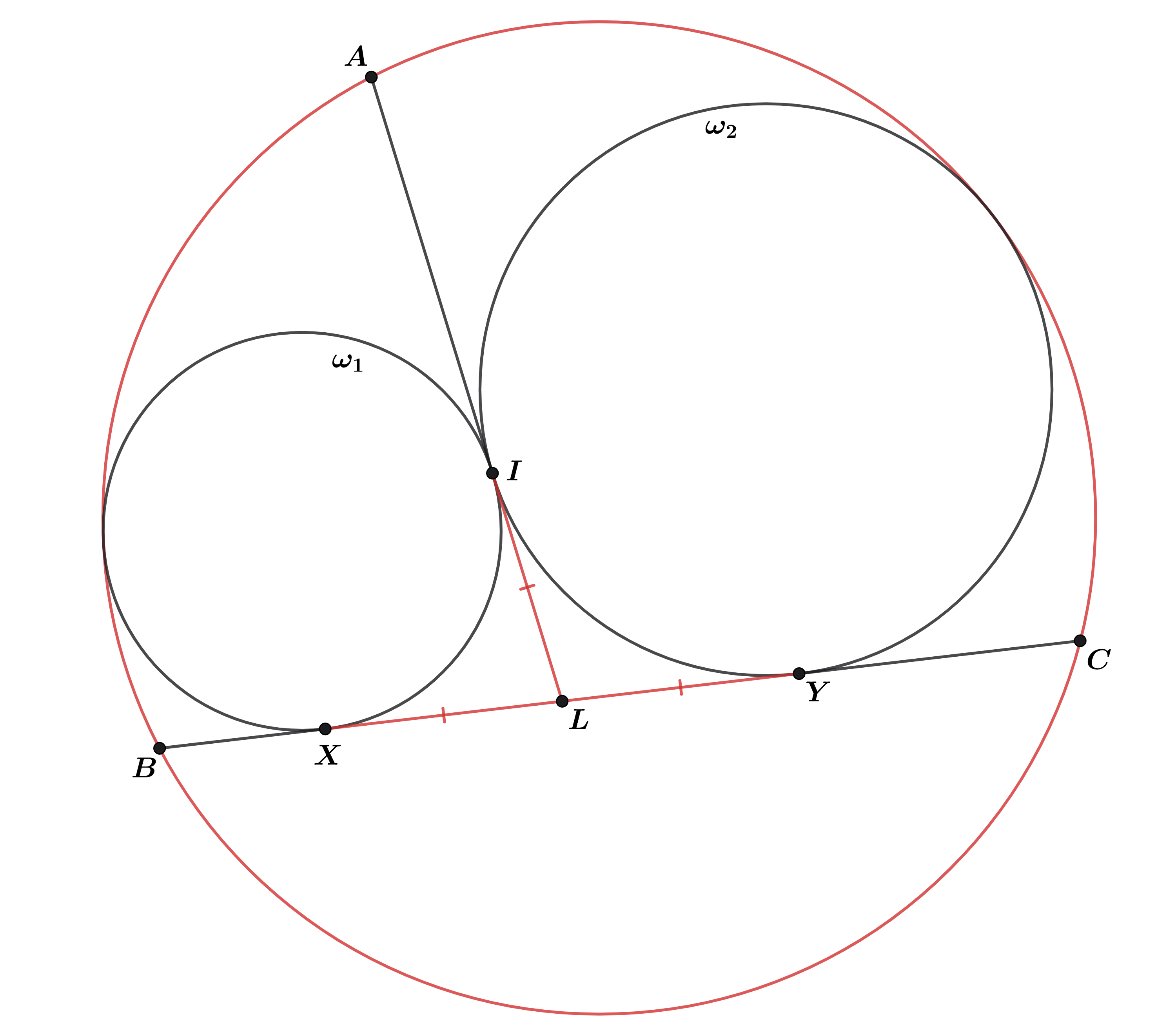
Пусть и
касаются прямой
в точках
и
соответственно, прямая
пересекает
в точке
Заметим, что
как длины касательных. Тогда, по теореме Кэзи для
имеем
Из следует, что
следовательно, соотношение переписывается в условие
что равносильно основному свойству биссектрисы для треугольника Таким образом,
— биссектриса треугольника
Аналогично
— биссектриса угла
т.е
является центром вписанной окружности треугольника.
Ошибка.
Попробуйте повторить позже
В треугольнике на стороне
взята точка
Рассмотрим окружность, касающуюся отрезка
в точке
отрезка
и
окружности, описанной около треугольника
Докажите, что прямая, проходящая через
параллельно
касается окружности,
вписанной в треугольник
Обозначим нашу окружность за а за
точку касания
и отрезка
Напишем теорему Кэзи для точек
и
окружности
Получаем:
Распишем отрезки и
как
и
соответственно. А отрезок
равен отрезку
поэтому его можно
записать как
Подставляем в наше равенство:
Все что с отрезком переносим в левую часть, а все что с отрезком
в правую и получаем:
Это равенство можно переписать так:
Где — периметр треугольника
Заметим, что в правой части (из формуле площади
) написано просто отношение
радиусов вписанных окружностей треугольников
и
А значит при гомотетии с центром в точке
который
переведет вписанную окружность треугольника
в вписанную окружности треугольника
точка
перейдет в
точку
следовательно касательная из
к вписанной окружности треугольника
будет параллельна
что и
требовалось.
![]()
Ошибка.
Попробуйте повторить позже
Теорема Геринга. Пусть и
— подмножества вершин графа
, а
Тогда верно одно из двух Утверждений:
Утверждение 1. В найдётся
-разделяющее множество мощности
Утверждение 2. В найдётся
непересекающихся путей из
в
(в том числе по вершинам множеств
и
(a) Докажите, что оба условия не могут выполняться одновременно.
(b) Докажите, что если Утверждение 1 неверно, то верно второе, индукцией по количеству вершин. Преобразуйте граф так, чтобы
-е утверждение не выполнялось, и при убирании некоторого ребра
существовало
-разделяющее множество
, где
Исследуйте множества
и
Ошибка.
Попробуйте повторить позже
Теорема Менгера. Пусть и
— две вершины связного графа
не соединенные ребром. Тогда наименьшее количество вершин
-разделяющего множества, не содержащего вершин
и
равно наибольшему количеству непересекающихся путей между
и
Ошибка.
Попробуйте повторить позже
Теорема Кёнига. Наибольшее количество рёбер в паросочетании в двудольном графе равно наименьшему количеству вершин в вершинном
покрытии графа (вершинное покрытие — это такое множество вершин, что каждое ребро содержит хотя бы одну из
них).
Ошибка.
Попробуйте повторить позже
Теорема Дирака. Пусть . В
-связном графе для любых
вершин существует простой цикл, содержащий все эти
вершины.
Ошибка.
Попробуйте повторить позже
Ошибка.
Попробуйте повторить позже
Неравенство Йенсена. Докажите, что если функция удовлетворяет условию выпуклости
то для любых неотрицательных сумма которых равна 1, и
из отрезка выпуклости, выполняется неравенство
Следствие. Если функция выпукла вверх, то выполнено неравенство
Ошибка.
Попробуйте повторить позже
Пусть
— неотрицательные числа. Докажите неравенство
Ошибка.
Попробуйте повторить позже
Действительные числа принадлежат промежутку
Докажите неравенство
Ошибка.
Попробуйте повторить позже
Для положительных чисел
и
докажите неравенство
Ошибка.
Попробуйте повторить позже
Вписанная окружность треугольника касается сторон
и
в точках
и
соответственно. Точка
— центр вневписанной
окружности, касающейся стороны
Точки
и
— середины
и
Прямые
и
пересекаются в точке
Докажите, что
лежит на описанной окружности треугольника
Подсказка 1
Раз есть центр вневписанной окружности и какие-то серединки, то можно отметить и центр вписанной, и середину дуги BC и воспользоваться леммой о трезубце! Что теперь можно заметить на картинке?
Подсказка 2
А вот что: т.к. середина дуги BC (пусть это W) является серединой отрезка между центрами вписанной и вневписанной окружностями, то WM и WN - средние линии в соответствующих треугольниках! А что еще про WM и WN можно сказать тогда?
Подсказка 3
Что они равны, т.к. соответствующие им основания - радиусы вписанной) А теперь вспомним, что WB = WC. Посчитайте уголки BWM и CWN, и тогда дальше досчитаются все уголки)
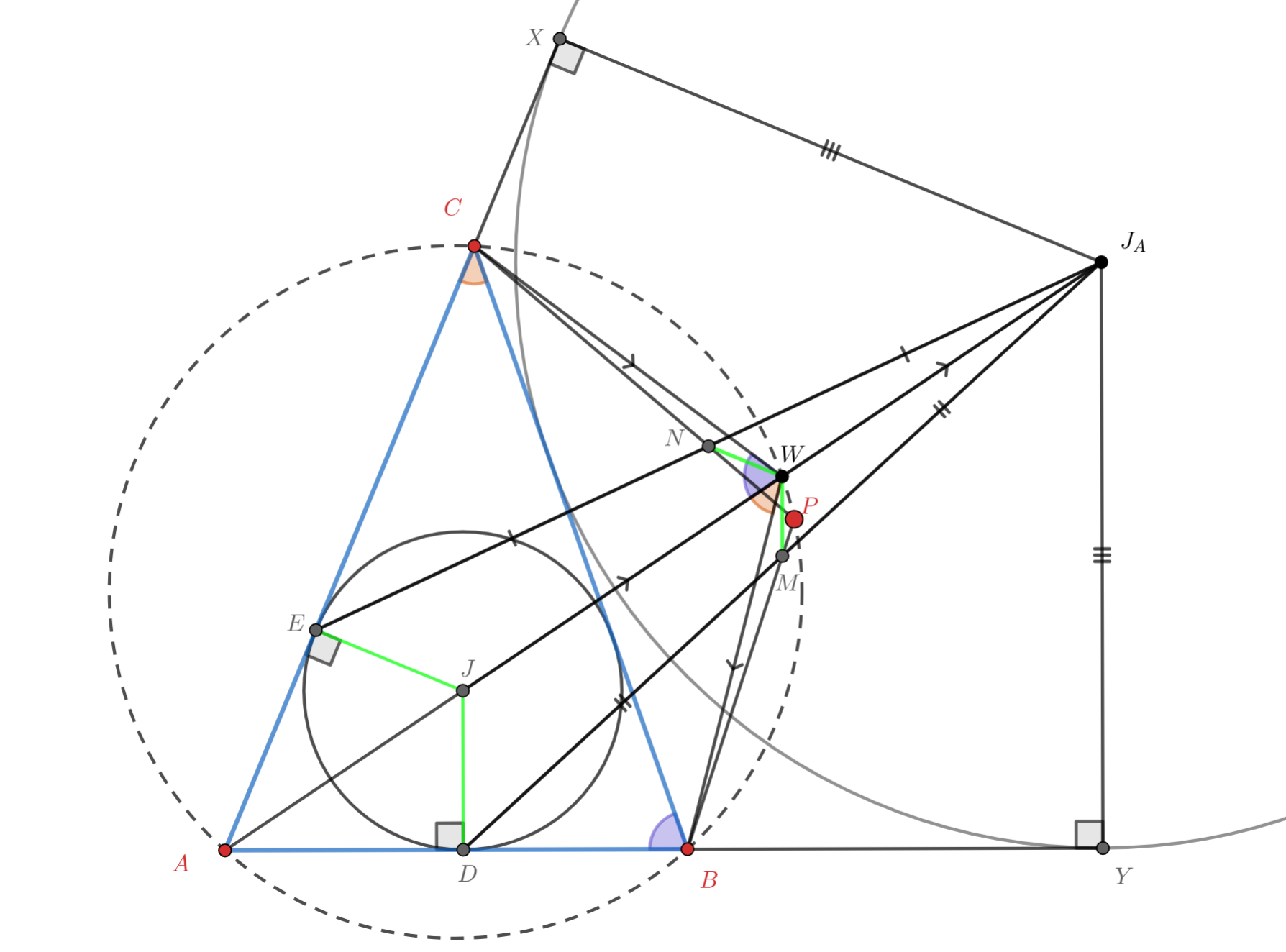
Первое решение. Пусть и
— центры вписанной и вневписанной окружностей
соответственно, a
— точка пересечения
описанной окружности
с биссектрисой
. Тогда по лемме о трезубце
. Проведем радиусы
и
.
Рассмотрим
и
.
и
являются средними линиями этих треугольников соответственно (так как
и
по условию). Так как
(как радиусы), то и
Пусть
Посчитаем .
Посчитаем .
Отсюда получается, что — вписанный
лежит на описанной
окружности
______________________________________________________________________________________________________________________________________________________
Второе решение. Достаточно доказать, что
Пусть — отражение точки
относительно
тогда
является средней линией треугольника
а значит,
Аналогично, если
— отражение
относительно
то
то есть достаточно проверить, что точки
лежат на одной окружности.
.png)
Учитывая, что лежит на биссектрисе угла
для этого достаточно показать, что
и
Последнее верно, если
треугольник
неравнобедренный, поскольку
Докажем, что Действительно, пусть
— точка касания вписанной окружности со стороной
тогда
и
симметричны относительно биссектрисы
внешнего угла
то есть
Аналогично,
.png)
Ошибка.
Попробуйте повторить позже
Найдите все пары действительных чисел удовлетворяющих равенству
Ошибка.
Попробуйте повторить позже
Определите все натуральные числа имеющие ровно
натуральных делителей (включая
и само число
Ошибка.
Попробуйте повторить позже
Докажите, что в разложение произведения десяти последовательных трёхзначных чисел на простые множители входит не больше
различных простых чисел.
Ошибка.
Попробуйте повторить позже
Собственным делителем числа называется любой его натуральный делитель, кроме и самого числа. С составным натуральным числом
разрешается проделывать следующие операции: разделить на наименьший собственный делитель или прибавить любое натуральное
число, делящееся на его наибольший собственный делитель. Если число получилось простым, то с ним ничего нельзя делать. Верно ли, что с
помощью таких операций из любого составного числа можно получить число
Ошибка.
Попробуйте повторить позже
Существует ли такое натуральное число, что произведение всех его натуральных делителей (включая и само число) оканчивается ровно
на
ноль?
Ошибка.
Попробуйте повторить позже
Докажите, что существует бесконечное число пар таких соседних натуральных чисел, что разложение каждого из них содержит любой
простой сомножитель не менее чем во второй степени. Примеры таких пар чисел:



