Регион до 2015
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
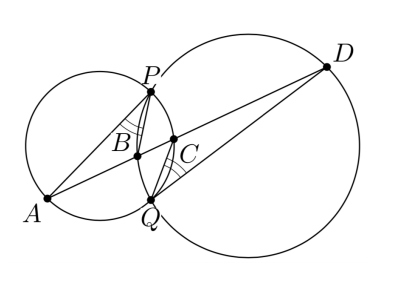
Серединный перпендикуляр к стороне неравнобедренного остроугольного треугольника
пересекает прямые
и
в
точках
и
соответственно, а серединный перпендикуляр к стороне
пересекает прямые
и
в точках
и
соответственно. Описанные окружности треугольников
и
пересекаются в точках
и
Докажите, что центр описанной
окружности треугольника
лежит на прямой
Источники:
Подсказка 1
Возникает вопрос, где взять центр описанной окружности, как связать с ним объекты из задачи. Очень просто, для этого достаточно вспомнить его определение.
Подсказка 2
Давайте заметим, что PQ - радикальная ось окружностей. Значит, если мы найдём ещё одну окружность такую, что O будет радикальным центром тройки окружностей, то задача будет решена.
Подсказка 3
Стоит обратить внимание на четырёхугольник B_1B_2C_2C_1. Если вы докажете, что он вписанный, то задачу решите.
Обозначим середины и
точками
и
соответственно, а точку пересечения серединных перпендикуляров
и
через
это и есть центр описанной окружности. Заметим, что если доказать, что четырёхугольник
— вписанный, то для
тройки окружностей
и
точка
будет радикальным центром и мы получим требуемое. Докажем
это.
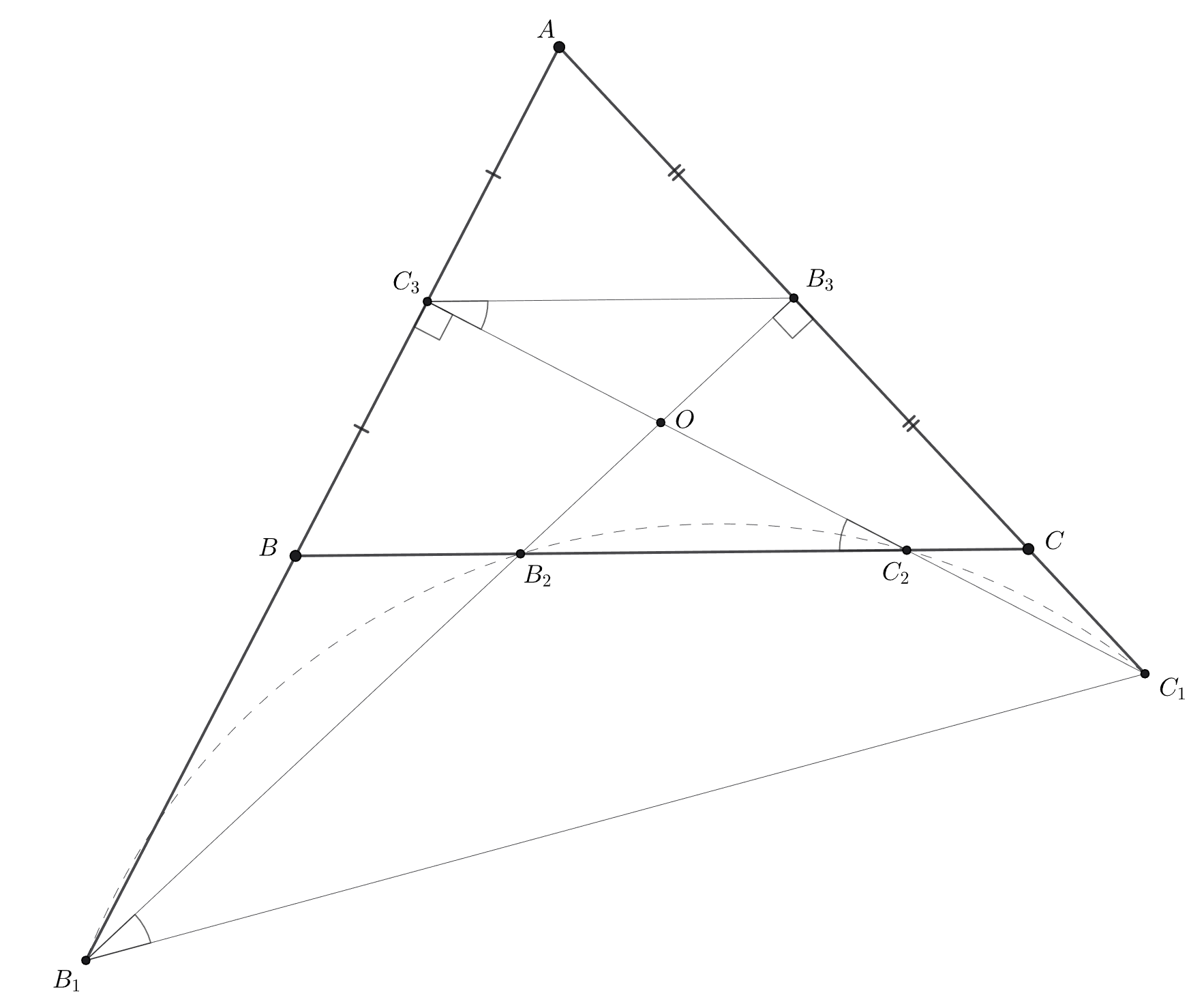
Заметим, что четырёхугольник вписанный, так как равные углы
и
стягивают
Следовательно,
Отрезок — средняя линия в
поэтому
Отсюда имеем
Из равенства
следует требуемое.
Ошибка.
Попробуйте повторить позже
Окружность, вписанная в прямоугольный треугольник с гипотенузой
касается сторон
в точках
соответственно. Пусть
– высота треугольника
Докажите, что точка
лежит на биссектрисе угла
Источники:
Подсказка 1
Попробуем посчитать углы! Что можно сказать об углах внутри четырёхугольника CA₁HB₁? Нам бы очень хотелось узнать что-то интересное про точку H ;)
Подсказка 2
Угол AHC — прямой! Что тогда можно сказать про точку H? Как связать её с нашим большим треугольником?
Подсказка 3
Подумайте, в каких точках пересекет A₁C₁ окружность, построенная на AC, как на диаметре! Сколько их таких и каким свойством они обладают?
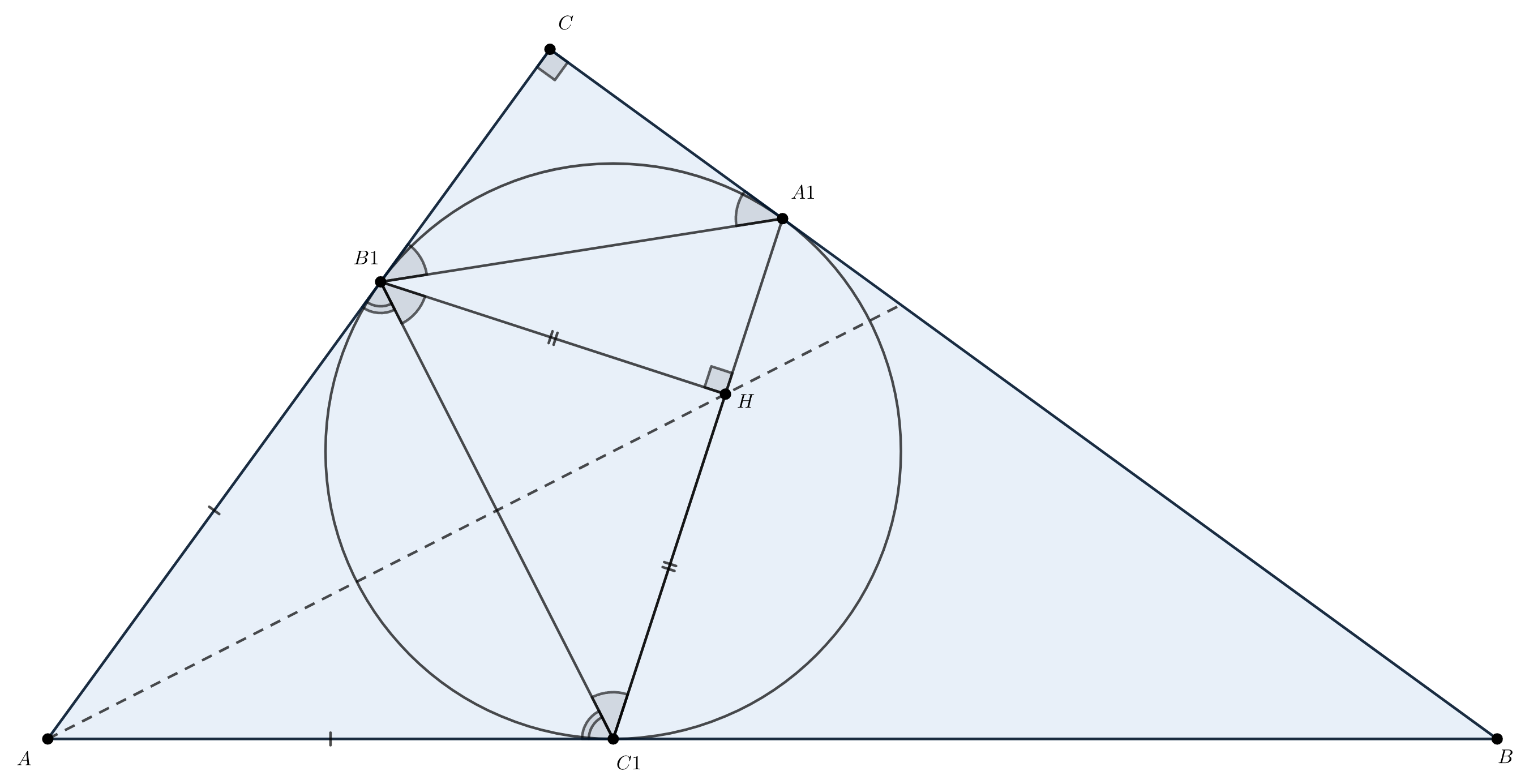
Заметим, что По теореме об угле между хордой и касательной
Таким образом,
треугольник
— равнобедренный. Треугольники
и
равны по третьему признаку (
как отрезки
касательных). Следовательно,
Ошибка.
Попробуйте повторить позже
На стороне треугольника
отмечена точка
Точки
и
симметричны точке
относительно биссектрис углов
и
Докажите, что середина отрезка
лежит на прямой
где
и
– точки касания вписанной окружности треугольника
со сторонами
и
Подсказка 1
При отражении точки D появились равные углы с вершиной в I. При подсчёте каких углов нам может это помочь?
Подсказка 2
Попробуем посчитать ∠EIB при помощи углов с этой же вершиной. А что еще мы знаем об углах с вершиной в центре вписанной окружности?
Подсказка 3
∠AIC = 90° + ∠B/2! Получается, при помощи ∠AIC можно связать ∠EIB и ∠B!
Подсказка 4
Что тогда можно сказать о четырёхугольнике IEBF?
Подсказка 5
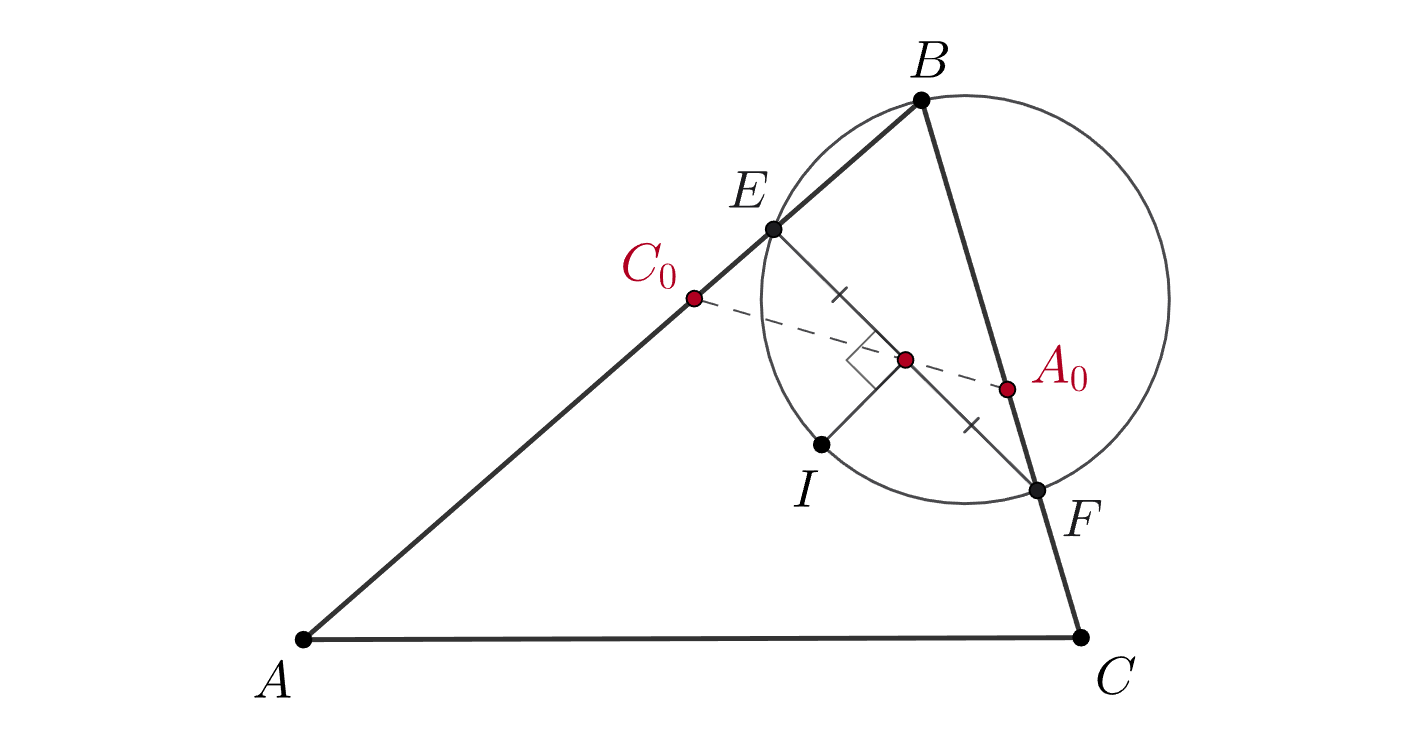
Четырёхугольник IEBF — вписанный! А что можно сказать о точках A₀ и C₀ относительно треугольника EBF? Можно ли так же связать точку M с ними?
Подсказка 6
A₀ и C₀ — основания перпендикуляров из точки I на стороны треугольника EBF. Хочется, чтобы M обладала таким же свойством ;)
Из симметрии относительно соответствующих биссектрис имеем равенства углов
следовательно, четырехугольник вписанный.
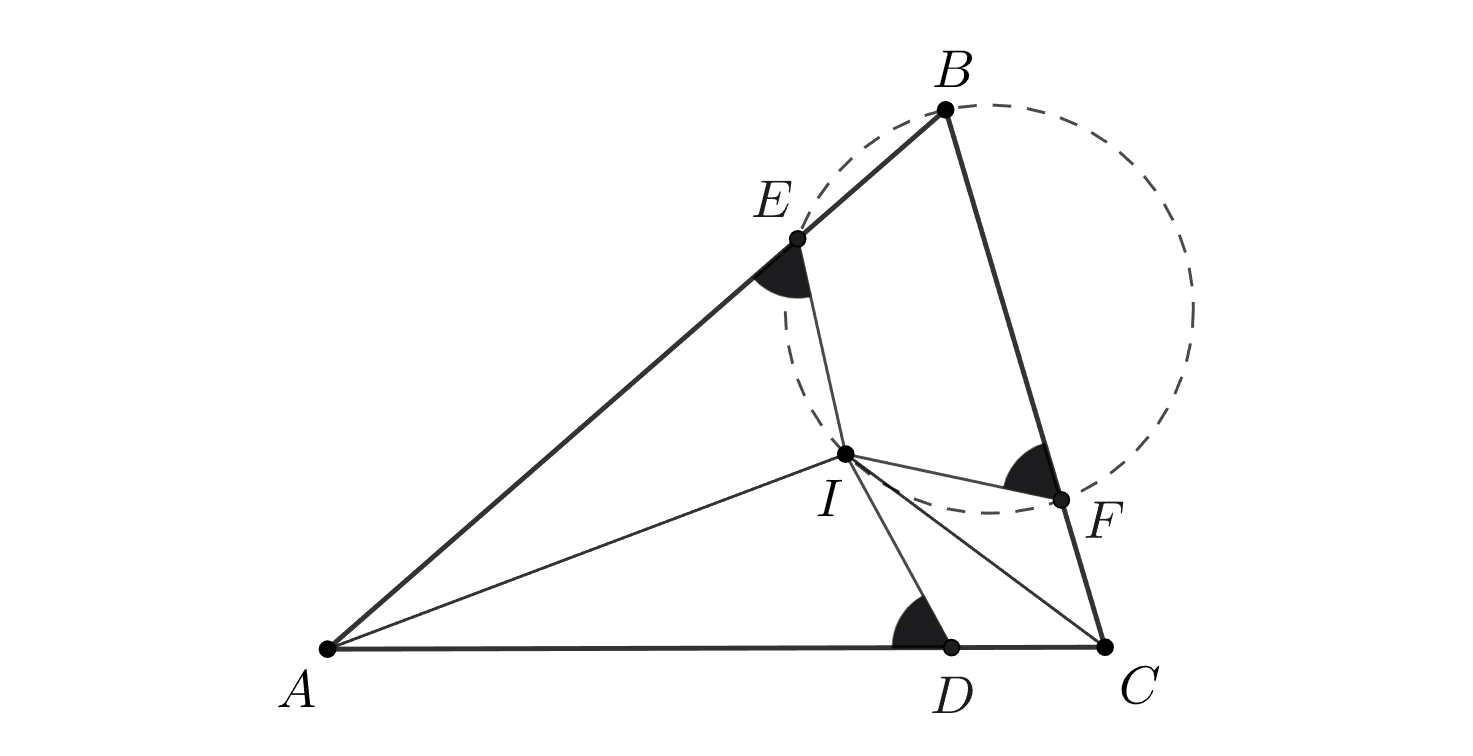
Осталось заметить, что и середина
являются основаниями перпендикуляров из точки
на стороны треугольника
а
значит, лежат на прямой Симсона указанной точки.
Ошибка.
Попробуйте повторить позже
Прямая касается описанной окружности треугольника
. Пусть
и
– основания перпендикуляров, опущенных из
на
прямые
,
. Докажите, что
.
Источники:
![]()
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
. Прямая, перпендикулярная стороне
и проходящая через
точку
, пересекает прямую
в точке
. Докажите, что угол
прямой.
Источники:
Подсказка 1
Нам дано три высоты, а значит, нужно вспомнить про ортоцентр и его свойства! Например, какое из свойств ортоцентра может сказать нам что-то об углах С₁А₁А и АА₁В₁?
Подсказка 2
Ортоцентр является точкой пересечения биссектрис ортотреугольника! Теперь посчитайте уголочки и посмотрите на треугольник С₁А₁К. Какой он?
Подсказка 3
Он равнобедренный, так как А₁С является одновременно биссектрисой и высотой! Посмотрите на отрезок КС₁ и подумайте о расположении точек К и С₁ относительно прямой ВС.
Вспомним одно из свойств ортоцентра: - точка пересечения высот треугольника
- является точкой пересечения биссектрис
ортотреугольника
______________________________________________________________________________________________________________________________________________________
Доказательство.
![]()
______________________________________________________________________________________________________________________________________________________
Пусть Проведём
и применим факт выше

Ошибка.
Попробуйте повторить позже
В трех школах города учится по 100 человек. Любые двое либо знакомы, либо не знакомы. Докажите, что можно выбрать двух школьников
и
из разных школ так, чтобы среди учащихся оставшейся школы нашлось либо 17 человек, каждый из которых знает и
и
либо 17 человек, каждый из которых не знает ни
ни
Введём граф, вершинами которого являются ученики, а рёбра соединяют учеников из разных школ. Покрасим ребро в синий, если двое знакомы, и в красный — если не знакомы. Назовём синей или красной галочкой тройку учащихся из разных школ, где один из них соединён рёбрами одинакового цвета с двумя другими.
Посчитаем общее число таких галочек. Каждые трое учеников из разных школ образуют хотя бы одну галочку: между ними три рёбра, и по принципу Дирихле найдутся два одного цвета, которые и задают нужную конструкцию. Таких троек всего
Рассмотрим, на какие пары учеников из разных школ опираются галочки — то есть те двое, которые не являются главным учеником. Таких пар
так как выбираем по паре из каждой пары школ.
По принципу Дирихле найдётся хотя бы одна пара, на которую приходится не менее
галочек. Среди них, по тому же принципу, хотя бы 17 одного цвета. Это означает, что найдутся ученики и
из двух школ, а в
третьей — по крайней мере 17 человек, которые либо все знают и
и
либо ни один из них не знаком ни с
ни с
что и
требовалось доказать.
Ошибка.
Попробуйте повторить позже
25 мальчиков и несколько девочек собрались на вечеринке и обнаружили забавную закономерность. Если выбрать любую группу не меньше чем из 10 мальчиков, а потом добавить к ним всех девочек, знакомых хотя бы с одним из этих мальчиков, то в получившейся группе число мальчиков окажется на 1 меньше, чем число девочек. Докажите, что некоторая девочка знакома не менее чем с 16 мальчиками.
Источники:
Подсказка 1:
После прочтения условия у вас сразу должно возникнуть желание рассмотреть группу из всех 25 мальчиков. Сколько тогда всего девочек?
Подсказка 2:
Итак, имеется ровно 26 девочек. Теперь будет разумно рассмотреть какую-нибудь группу из 24 мальчиков, ведь с ней тоже довольно просто работать. Также вместе с этим стоит рассмотреть мальчика, не вошедшего в группу, и девочку, которую нельзя к ним добавить. С кем она знакома, а с кем — нет?
Подсказка 3:
Эта девочка знакома только с мальчиком, не вошедшим в группу. Получается, что для каждого мальчика существует такая девочка. А что можно сказать про 26-ю девочку, у которой нет такой пары?
По условию имеется ровно 26 девочек, знакомых хотя бы с одним мальчиком из 25. Рассмотрим какую-то группу из
мальчиков. По условию ей соответствует группа из
девочек. Рассмотрим мальчика
и девочку
не вошедших в
соответствующие группы. Они знакомы, потому что
должна быть знакома хотя бы с одним мальчиком. Также
не
знакома с остальными
мальчиками. Если рассматривать другие группы из
мальчиков, становится ясно, что для
каждого мальчика есть девочка, знакомая только с ним. Рассмотрим оставшуюся
-ю девочку. Предположим, что она
знакома менее, чем с 16 мальчиками. Тогда остальные
мальчиков знакомы ровно с
девочками, что противоречит
условию.
Ошибка.
Попробуйте повторить позже
Известно, что сумма цифр натурального числа равна
а сумма цифр числа
равна
Докажите, что
чётно.
Источники:
Подсказка 1
Для начала подумаем над тем, какое число имеет такую же сумму цифр, что и число N и при этом, чтобы это число несложно получалось из числа 5N
Подсказка 2
Да, это число 10N. Тогда мы знаем, что 5N + 5N = 10N. А что можно заметить про сумму цифр?
Подсказка 3
Верно, для суммы цифр справедливо такое же равенство(из условия). Тогда мы понимаем, что при сложении 5N с самим собой нет перехода через разряд! Остаётся проверить, может ли N быть нечётным!
Подсказка 4
Если N нечётно, то его последняя цифра тоже нечётна. А не случиться ли перехода через разряд, если мы сложим последнюю цифру числа 5N с собой же?
Обозначим за сумму цифр числа
При сложении чисел сумма цифр не увеличивается, а при умножении на 10 сумма цифр не
меняется, поэтому
Значит, в неравенстве должно достигаться равенство. Это произойдёт, если при сложении с
не будет переносов через
разряд.
Предположим, что нечётно. Значит,
оканчивается нечётной цифрой. Заметим, что произведение
и любой нечётной цифры
оканчивается на
, но тогда и
оканчивается на
. В таком случае при суммировании
и
перенос произойдёт при сложении
цифр в разряде единиц. Пришли к противоречию. Значит,
не может быть нечётным.
Ошибка.
Попробуйте повторить позже
В треугольнике (
<
)
— центр вписанной окружности
— середина
— середина дуги
описанной
окружности треугольника. Докажите, что
=
Источники:
Пусть описанная окружность треугольника является единичной с центром в нуле, а также треугольник
положительно
ориентирован. Пусть
— комплексное число с единичным модулем, такое, что
попадает в середину дуги
и
попадает в точку
аналогично определим число
(
— середина дуги
совпадает с
). Тогда середина дуги
имеет координату
Центр вписанной окружности имеет координату
(как было доказано на вебинаре). Точка
имеет координату
Осталось проверить, что число
— вещественное. Подставив все найденные выражения,
получаем
Последнее выражение действительно вещественное, что легко видно после замены ,
Ошибка.
Попробуйте повторить позже
Два игрока по очереди выписывают на доске в ряд слева направо произвольные цифры. Проигрывает игрок, после хода которого одна
или несколько цифр, записанных подряд, образуют число, делящееся на Кто из игроков победит при правильной
игре?
Источники:
Обозначим цифры, выписываемые игроками, последовательно через цифры с нечётными номерами выписывает первый, а с чётными —
второй. Рассмотрим остатки
от деления на
знакопеременных сумм
Согласно признаку делимости на после
го хода на доске возникнет число, кратное
тогда и только тогда, когда
совпадает с одним из
Расположим эти остатки по кругу по часовой стрелке от
до
и изобразим
последовательность ходов как процесс перемещения по кругу по неповторяющимся остаткам
При этом первый игрок
м ходом
"прибавляет"к
любое число
от
до
а второй — любое число от
до
Таким образом, кроме повтора
уже встречавшегося остатка, первому игроку запрещён ход против часовой стрелки на
а второму — ход по часовой
стрелке на
После
го хода свободными останутся
остатков. Игрок гарантированно может сделать ход, если
есть хотя бы два свободных остатка, значит, первые восемь ходов игроки сделать смогут, а
й ход сделать нельзя
никогда.
Рассмотрим ситуацию после седьмого хода (это ход первого), когда свободны остатка. Разберём три случая.
Свободные остатки расположены подряд:
Тогда второй выписывает число с остатком
(занимает остаток
), первый
—
а второй
и выигрывает.
Остатки расположены так: два рядом —
и один отдельно —
Тогда второй занимает один из остатков
далее либо
первый занимает остаток
второй —
и выигрывает, либо первый занимает
а второй — один из оставшихся
и
выигрывает.
Никакие два остатка не стоят рядом:
Тогда второй может занять один из них и после хода первого, второй может занять
последний свободный остаток и выиграть.
Второй игрок
Ошибка.
Попробуйте повторить позже
На плоскости расположено прямоугольников со сторонами, параллельными осям координат. Известно, что любой
прямоугольник пересекается хотя бы с
прямоугольниками. Доказать, что найдется прямоугольник, пересекающийся со всеми
прямоугольниками.
Спроецируем все прямоугольники на оси координат. Рассмотрим сначала проекции на ось для каждого прямоугольника получим
отрезок
Выберем:
- Самый левый из всех правых концов проекций:
- Самый правый из всех левых концов проекций:
Заметим, что точка принадлежит как минимум
отрезку. Аналогично, точка
принадлежит как минимум
отрезку.
Тогда общее количество отрезков, содержащих хотя бы одну из этих точек, не менее
Поскольку всего отрезков то количество отрезков, содержащих обе точки
и
будет:
Заметим, что такие отрезки пересекают все остальные, так как в них полностью лежит отрезок а его все пересекают по выбору
Аналогичные рассуждения проводим для проекций на ось
Суммарное количество “хороших” проекций на обеих осях:
Покажем, что это число превышает общее количество прямоугольников:
Это неравенство выполняется, так как для целой части справедливо:
По принципу Дирихле существует хотя бы один прямоугольник, проекции которого на каждую ось пересекаются с проекциями любого другого прямоугольника. Покажем, что он пересекается с любым другим. Предположим, что существует прямоугольник, не пересекающий данный, тогда найдется вертикальная или горизонтальная прямая, разделяющая их. Тогда точка пересечения данной прямой с осью координат разделяет соответствующие проекции.
Ошибка.
Попробуйте повторить позже
Саша написал на доске ненулевую цифру и приписывает к ней справа по одной ненулевой цифре, пока не выпишет миллион цифр.
Докажите, что на доске не более раз был написан точный квадрат.
Рассмотрим отдельно числа из нечетного и из четного числа знаков.
Пусть — встретившиеся на доске квадраты из четного количества знаков, и в их записи содержится соответственно
цифр. Аналогично, пусть
— встретившиеся на доске квадраты из нечетного количества знаков, и в их
записи содержится соответственно
цифр.
Число содержит
цифр и не оканчивается на
поэтому
откуда
Число
получается из
приписыванием некоторого четного количества — обозначим его
— ненулевых цифр. Поэтому
Из
левого неравенства получаем
следовательно,
откуда
т. е.
Из этого неравенства следует, что
содержит не более
цифр, т. е.
тогда из неравенства
следует
откуда
Аналогичное рассуждение применимо к последовательности
получается приписыванием к
цифр,
и
т. е.
Теперь заметим, что в каждой из
последовательностей
и
меньше
членов (так как
и
и
должны быть не меньше, чем
).
Итак, всего квадратов на доске окажется не более
Ошибка.
Попробуйте повторить позже
На стороне треугольника
выбрана точка
Окружность, описанная около треугольника
пересекает сторону
в точке
а окружность, описанная около треугольника
пересекает сторону
в точке
Пусть
— центр описанной окружности треугольника
Докажите, что прямая
перпендикулярна стороне
Обозначим Из условия задачи следует, что четырёхугольник
— вписанный, причём точки
и
лежат по одну сторону от прямой
поэтому
Поскольку
— центральный угол этой
окружности, а
— вписанный, то
Четырёхугольники
и
— вписанные,
поэтому
Значит,
поэтому
т.е. четырёхугольник также вписан в некоторую окружность. Вписанные углы
и
этой окружности
опираются на равные хорды
и
(радиусы описанной окружности треугольника
), значит, они равны. Тогда
а т.к. углы
и
— смежные, то каждый из них равен
Следовательно,
.png)
Ошибка.
Попробуйте повторить позже
В треугольнике на стороне
нашлись такие точки
и
что
и
между
и
Точка
—
середина дуги
окружности, описанной около треугольника
Докажите, что точки
лежат на одной
окружности.
Источники:
Подсказка 1
Самое важное -- понять, как использовать середину дуги. Вспомним, что середина дуги является точкой пересечения биссектрисы угла А и серединного перпендикуляра к BC.
Подсказка 2
Но по условию точка Е тоже равноудалена от вершин В и С, так что EF является серединным перпендикуляром к BC. Попробуйте выразить угол BFE через угол А!
Подсказка 3
Осталось доказать, что он равен углу BDE. Но выразить угол BDE через угол А ещё проще, ведь это угол при основании равнобедренного треугольника с углом А при вершине.
Подсказка 4
Если получилось реализовать хотя бы один из пунктов подсказок -- у Вас уже есть зацепка, какое условие осталось доказать для решения задачи. Удачи!
Первое решение.
Пусть Отсюда
и
![]()
Поскольку — середина дуги
то
и
(в силу
равны
).
Поэтому
откуда и следует вписанность
______________________________________________________________________________________________________________________________________________________
Второе решение.
Обозначим углы треугольника как
. Проведем
— медиану, биссектрису и высоту равнобедренного треугольника
. Докажем, что
.
.png)
так как
— серединный перпендикуляр к
.
так как
как вписанные, опирающиеся на одну дугу
. Итого
Ошибка.
Попробуйте повторить позже
Две окружности и
пересекаются в точках
и
. Прямая пересекает последовательно окружности
в точках
соответственно. Докажите, что
Источники:
Подсказка 1
Когда есть пересекающиеся окружности -- немедленно стоит провести общую хорду! Так можно будет поработать с углами: поперекидывать вписанные углы из одной окружности через общую хорду в другую окружность
Подсказка 2
Осталось учесть теорему о внешнем угле треугольника и аккуратно выразить нужные углы
Вписанные в левую окружность углы, опирающиеся на дугу равны:
Так как — внешний угол треугольника
то
Вписанные в правую окружность углы, опирающиеся на дугу равны:
Угол равен сумме углов
и
таким образом,
Получаем
Ошибка.
Попробуйте повторить позже
На доске записаны числа 1, 2, 3, …, 1000. Двое по очереди стирают по одному числу. Игра заканчивается, когда на доске остаются два числа. Если их сумма делится на три, то побеждает тот, кто делал первый ход, если нет — то его партнер. Кто из них выиграет при правильной игре?
Первый способ. Сначала попробуем применить уже известную нам симметричную стратегию для второго игрока. Разобьем все числа на
пары: 1 — 1000, 2 — 999, ..., 500 — 501 (то есть пары чисел, которые в сумме дают 1001). Если первый игрок стер число , то второй стирает
парное ему число —
. То есть после хода второго в каждой паре числа либо оба стерты, либо оба остались. Следовательно, два
последних числа будут обязательно из одной пары, то есть их сумма будет ровно
, что не делится на 3. Таким образом второй всегда
побеждает.
Второй способ. Теперь попробуем порешать эту задачу другим методом. Проанализируем момент, когда какой-то игрок побеждает
или проигрывает, то есть последний ход. Так как последний ход четный, то его совершает именно второй игрок. Тогда
перед последним ходом второго у нас осталось 3 числа. Какое число нужно выбрать в этот момент второму, чтобы он
победил? Ему нужно оставить числа, сумма которых не кратна трем. Обозначим остатки по модулю 3 этих трех чисел за
.
Если среди них есть хотя бы два различных (пусть и
), то хотя бы одно из чисел
и
не кратно трем (если
оба кратны трем, то
и
совпадают с остатком числа
). Значит, у второго точно есть ход, после которого он
побеждает.
Значит, второй может проиграть, только если все три остатка равны, причем равны нулю (иначе сумма любых двух чисел не кратна трем, то есть второй обязательно побеждает). Тогда второму нужно не допустить такую ситуацию. Что нужно сделать, чтобы в конце точно не осталось трех нулей? Давайте каждым ходом второго игрока стирать числа, кратные трем (если такие еще есть). Тогда к последнему ходу второго вовсе не останется чисел, кратных трем (так как их сильно меньше половины всех чисел). То есть ситуации с тремя нулями точно не будет, и значит, второй победит.
Ошибка.
Попробуйте повторить позже
В треугольнике в котором
на стороне
выбрана точка
и вокруг треугольников
и
описаны
окружности
и
соответственно. Касательная, проведенная к
в точке
пересекает второй раз
в точке
Докажите, что
Источники:
Подсказка 1
Не стоит рисовать окружность -- они будут только захламлять чертёж и мешать работать с углами. Работайте с углами - Вам дана касательная и даны четыре точки на окружности S2
Подсказка 2
Отмечаем (вводим буквой альфа!) угол между касательной и хордой. Отмечаем (вводим букву бетта!) вписанные углы. Не забываем условие про равнобедренный треугольник - равные углы при основании
Подсказка 3
Теперь всё должно получиться -- проверьте, почему равны накрест лежащие углы при искомых прямых (выражаем их через альфа и бетта!)
![]()
Пусть Тогда
по свойствам касательной. Далее из вписанности
Для
доказательства параллельности достаточно равенства
Заметим, что
является суммой одной и двух
дужек и внешним для
откуда и следует
что и требовалось.
что и требовалось доказать



