Тема ДВИ в МГУ - задания по годам

ДВИ 2025

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дви в мгу - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 21#130848Максимум баллов за задание: 7

Дан куб с основаниями $ABCD,$ $A′B′C′D′$ и боковыми ребрами $AA′,$ $BB′,$ $CC ′,$ $DD ′.$ Длина ребра этого куба равна 1. На диагонали $AC$ основания $ABCD$ отмечена точка $E$ так, что $√2−1 AE = 2 .$ Найдите площадь сечения данного куба, проходящего через его центр $O$ и перпендикулярного прямой $OE.$

Источники: ДВИ - 2025, вариант 254, задача 7

Подсказки к задаче

Подсказка 1

Как нам построить желаемое сечение? Может, оно должно содержать какую-то прямую?

Подсказка 2

Рассмотрите плоскость ACC'.

Подсказка 3

Проведите в ней прямую, перпендикулярную OE, пусть точки T и K являются точками пересечения этой прямой с отрезками AC и A'C' соответственно. Можно ли найти еще одну прямую, перпендикулярную OE?

Подсказка 4

Рассмотрите проекцию OE на плоскость ABC. Попробуйте увидеть теорему о трех перпендикулярах.

Подсказка 5

Как теперь построить сечение? Может, надо провести какие-то параллельные прямые?

Подсказка 6

Например, можно провести через точку O прямую, параллельную BD.

Подсказка 7

А как удобнее было бы искать площадь сечения?

Подсказка 8

Можно ведь ее выразить через площадь проекции на некоторую плоскость и косинус угла!

Показать ответ и решение

Проведём прямую в плоскости $ACC′$ перпендикулярно $OE,$ пусть точки $T$ и $K$ являются точками пересечения этой прямой с отрезками $AC$ и $′ ′ A C$ соответственно.

$PIC$

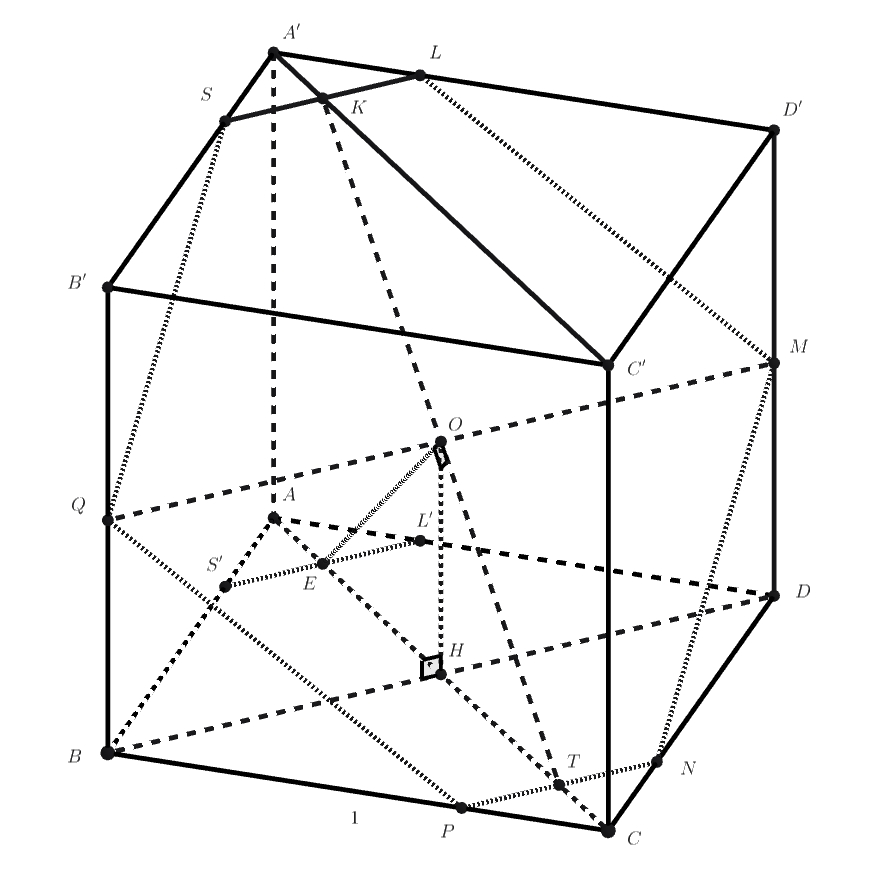
Заметим, что проекция $OE$ на плоскость $ABC$ перпендикулярна $BD,$ следовательно, по ТТП $BD ⊥ OE.$ Проведем через точки $T$ и $K$ прямые, параллельные $BD,$ точки пересечения этих прямых со сторонами квадратов $ABCD$ и $′ ′ ′ ′ A BC D$ соответственно принадлежат сечению. Если провести через точку $O$ прямую, параллельную $BD,$ то точки пересечения этой прямой с $′ BB$ и $′ DD$ также будут принадлежать сечению, соединив полученные 6 точек, мы построим наше сечение. Пусть $SLMNP Q$ — построенное сечение, $S ∈A ′B′,$ $L∈ A′D′,$ $M ∈DD ′,$ $N ∈DC,$ $P ∈BC$ и $Q∈ BB ′.$

Пусть $OH$ — проекция точки $O$ на плоскость $ABC.$

OH = 12

√ - AH =0.5AC = --2 2

√2- √2-− 1 1 EH = AH − AE = 2 − 2 = 2 = OH

Треугольник $△EOH$ прямоугольный равнобедренный, соответственно, $∘ ∠OEH = ∠EOH = 45.$ Заметим, что угол $∘ ∘ ∠HOT =90 − ∠HOE = 45 ,$ так что $△HOT = △HOE$ и $1 EH =HT =2.$ При этом угол $∠OTH$ — угол между плоскостью сечения и плоскостью $ABC,$ также равен $45∘.$

Спроецируем сечение на плоскость $ABC:$ проекциями точек $Q$ и $M$ являются точки $B$ и $D$ соответственно, проекции точек $S$ и $L$ назовем $S′$ и $L′.$ Найдём площадь шестиугольника $S ′L′DNP B:$

SS′L′DNPB = SABCD − SAS′L′ − SCPN = 1− SAS′L′ − SCPN =1 − 2SAS′L′

Из подобия треугольников $△AS ′E$ и $△ABH$ следует, что

′ √ - AS-= AE-= --2√− 1 AB AH 2

′ √2- AS =1− 2

Аналогично $′ √2 AL = 1− -2 .$

( √ -)2 SS′L′DNPB =1 − 2AS-′⋅AL-′=1 − 1 −-2 = √2 − 0.5 2 2

SS′L′DNPB √2-− 0.5 √2 SSLMNPQ = -cos∠OT-H-= -0.5√2--= 2− 2--

Ответ:

$√2- 2− 2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 22#131015Максимум баллов за задание: 7

Какое из следующих двух чисел больше: $4+ 2- 5 11$ или $6+ 1? 7 8$

Источники: ДВИ - 2025, вариант 255, задача 1

Подсказки к задаче

Подсказка 1

Для начала было бы неплохо сложить дроби.

Подсказка 2

Обратите внимание, что обе получившиеся дроби близки к единице. Как это может нам помочь при сравнении?

Подсказка 3

Попробуйте оценить расстояние от каждой из дробей до единицы!

Показать ответ и решение

Чтобы сравнить два числа, найдем их значения.

Вычислим первое число:

4 2 4⋅11+ 2⋅5 44+ 10 54 5 + 11 =--55----= --55--= 55

Вычислим второе число:

6 1 6 ⋅8 +1⋅7 48 +7 55 7 + 8 =--56--- = -56--= 56-

Теперь нам нужно сравнить получившиеся дроби. Сделать это можно, сравнив их “расстояние” до единицы.

Для первой дроби:

54= 1− -1 55 55

Для второй дроби:

55= 1− -1 56 56

Так как $-1 > 1, 55 56$ то из единицы мы в первом случае вычитаем большее число, а, значит, получаем меньший результат.

1− 1-< 1− 1- 55 56

Следовательно,

4+ 2-< 6 + 1 5 11 7 8

Ответ:

$6 + 1 7 8$

Ошибка.
Попробуйте повторить позже

Задача 23#131016Максимум баллов за задание: 7

Положим для каждого натурального $n$

1 1 1 An =1 +2 + 3 + ...+ n

Bn = A1+ A2+ A3+ ...+An

Найдите $B7+-7. A7$

Источники: ДВИ - 2025, вариант 255, задача 2

Подсказки к задаче

Подсказка 1

Значение А₇ нетрудно вычислить, а что делать с B₇?

Подсказка 2

По определению, Bₙ = A₁ + … + A₇. А чему равно Aₖ? Можно ли сгруппировать какие-то слагаемые?

Подсказка 3

Aₖ = 1 + 1/2 + … + 1/k. Сколько раз в Bₙ встретится слагаемое 1/n? А слагаемое 1?

Подсказка 4

Верно, 1 и n раз соответственно! А сколько раз в Bₙ встретится 1/k, где k ≤ n? Тогда для Bₙ можно будет записать вполне понятный ряд (сумму).

Подсказка 5

1/k встретится в Bₙ (n - k + 1) раз, где k ≤ n. Тогда Bₙ = ∑ ((n - k + 1) / k). Приведите этот ряд к более удобному виду.

Подсказка 6

(n - k + 1) / k ‎ = (n + 1) / k - k / k ‎ = (n + 1) / k - 1 ‎ = (n + 1) ⋅ (1/k) - 1.

Подсказка 7

Запишите отношение между Aₙ и Bₙ.

Показать ответ и решение

Найдем общее соотношение между $B n$ и $A . n$ По определению

∑n Bn = Ak = A1 +A2 +...+ An k=1

Перегруппируем слагаемые в этой сумме. Заметим, что слагаемое $1 k$ входит в каждое $Aj,$ где $j ≥ k.$ Таким образом, слагаемое $1 k$ в сумме для $Bn$ встретится $(n− k +1)$ раз. Тогда мы можем переписать $Bn$ следующим образом:

∑n (n +1)− k ∑n (n +1 k) ∑n (n +1 ) ∑n 1 ∑n Bn = ---k----= --k- − k = --k- − 1 =(n+ 1) k − 1 k=1 k=1 k=1 k=1 k=1

Учитывая, что

∑n 1= A и ∑n 1= n, k=1k n k=1

получаем общее соотношение:

Bn = (n +1)An− n

При $n =7$ имеем

B7 = (7 +1)A7− 7= 8A7 − 7

Подставим это выражение в искомую дробь:

B7A+-7= (8A7−A-7)+-7= 8AA7 = 8 7 7 7

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 24#131018Максимум баллов за задание: 7

Решите неравенство

(3√-)5+log2x 1+logx x ≥ 2 2

Источники: ДВИ - 2025, вариант 255, задача 3

Подсказки к задаче

Подсказка 1

Перед преобразованием нужно выписать ОДЗ!

Подсказка 2

В левой стороне неравенства степенная функция для x. Хотелось бы справа получить что-то подобное, только необходима проверка для x = 1.

Подсказка 3

Отлично, теперь у нас есть неравенство: xᶠ⁽ˣ⁾ ≥ xᵍ⁽ˣ⁾, где f(x) = (5 + log₂(x)) / 3, g(x) = 1 + logₓ(2). Теперь самое время вспомнить про рационализацию! Какое неравенство получится?

Подсказка 4

Получим (x - 1) ⋅ ((5 + log₂(x)) / 3 - 1 - logₓ(2)) ≥ 0. Будем находить нули каждой скобки по отдельности. Для второй понадобится замена, какая?

Подсказка 5

Пусть t = log₂(x). Чему тогда равен logₓ(2)?

Подсказка 6

По свойствам логарифмов logₓ(2) = 1/log₂(x). Получим квадратное уравнение относительно t, останется только сделать обратную замену, расставить знаки и не забыть про ОДЗ.

Показать ответ и решение

Запишем ОДЗ:

x> 0

Преобразуем исходное неравенство

x5+lo3g2x-≥ 2⋅2log2x

x5+log32x-≥2 ⋅x

Если $x= 1,$ то неравенство не будет выполняться:

153 ≥ 2

Если $x⁄= 1,$ то на ОДЗ будет верно следующее:

x5+lo3g2x-≥xlogx2⋅x

5+log2x x--3---≥ x1+logx2

По методу рационализации

( 5+ log2x ) (x− 1) ---3---− 1− logx2 ≥ 0

(x − 1)(2+log2 x− 3 logx2)≥0

( --3-) (x− 1) 2+ log2x− log2x ≥ 0

Найдем $x,$ при которых вторая скобка обращается в 0:

3 2+ log2x −log-x = 0 2

Пусть $log2x= t.$ Так как $x ⁄=1,$ $t⁄= 0.$

2+t− 3 =0 t

2 t + 2t− 3= 0

(t+ 3)(t− 1)= 0

t∈{−3;1}

Сделаем обратную замену:

log2x= −3 ⇔ x= 18

log2x= 1⇔ x =2

По методу интервалов получаем:

( ] x∈ −∞; 1 ∪ [2;+∞) 8

На пересечении с ОДЗ

( 1] x∈ 0;8 ∪[2;+ ∞)

Ответ:

$(0;1 ]∪[2;+∞ ) 8$

Ошибка.
Попробуйте повторить позже

Задача 25#131019Максимум баллов за задание: 7

Решите уравнение

(1−-tg2x)(1+-sin2x) 2 (1+ tg2x)(1− sin2x) = 3+ 2sin2x− 2sin x

Источники: ДВИ - 2025, вариант 255, задача 4

Подсказки к задаче

Подсказка 1

Начинаем с ОДЗ перед преобразованием и пробуем упростить выражение (1 - tg²(x))/(1+tg²(x)).

Подсказка 2

Для упрощения используем выражения тангенса через синус и косинус. Что теперь получилось в левой части?

Подсказка 3

В левой части будет cos(2x)⋅(1+sin(2x))/(1-sin(2x)). Перейдем к правой части. Попробуйте применить формулу понижения степени.

Подсказка 4

Справа будет следующее выражение: 2+2sin(2x)+cos(2x). С дробями работать неудобно, домножим обе части уравнения на (1-sin(2x)).

Подсказка 5

Осталось раскрыть скобки, получим произведение двух множителей, равное нулю. Расписываем два случая и помним про ОДЗ.

Показать ответ и решение

Сначала определим ОДЗ. Тангенс определен, если $cosx ⁄=0,$ то есть $x⁄= π +πk,k∈ ℤ. 2$ Знаменатель дроби не должен быть равен нулю. Так как

2 1 1+tg x= cos2x-⁄= 0

при $cosx ⁄= 0,$ то второе условие: $1− sin2x⁄= 0.$ Отсюда $sin2x⁄= 1,$ то есть

π 2x ⁄= 2 + 2πk

Теперь преобразуем обе части уравнения.

Начнем с левой части. Воспользуемся известными тригонометрическими тождествами:

2 1− sin2x- cos2-x− sin2x 11−+-ttgg2-xx =---csoins22xx-= cos2coxs2+sxin2x-= cos12x-= cos2x 1+ cos2x- ---cos2-x---

Тогда левая часть уравнения принимает вид:

cos2x ⋅ 1+-sin2x 1− sin2x

Преобразуем правую часть уравнения, используя формулу понижения степени $2sin2x =1 − cos2x$ :

3+ 2sin2x− 2sin2x= 3+ 2sin2x− (1 − cos2x)= 2+ 2sin2x+ cos2x

Приравняем преобразованные части с учетом ОДЗ:

cos2x ⋅ 11+−s siinn22xx = 2+ 2sin2x+ cos2x

Домножим обе части на $(1− sin2x) ⁄=0$ :

cos2x(1 +sin 2x)= (2+2 sin2x+cos2x)(1− sin2x)

Раскроем скобки:

cos2x+ cos2xsin2x =2(1+ sin2x)(1− sin2x)+cos2x(1− sin2x)

2 cos2x +cos2x sin2x= 2(1− sin 2x)+cos2x− cos2xsin2x

cos2x+ cos2xsin2x = 2cos22x+ cos2x− cos2xsin2x

Перенесем все члены в одну сторону:

2cos2xsin2x− 2cos22x= 0

Вынесем общий множитель $2cos2x$ за скобки:

2cos2x(sin2x− cos2x)=0

Это уравнение распадается на два:

cos2x =0

2x = π+ πk,k ∈ℤ 2

Отсюда

sin 2x = ±1

Учитывая ОДЗ ( $sin2x⁄= 1$ ), мы должны исключить случаи, когда $sin2x =1.$ Следовательно, нам подходит только

sin 2x = −1

Это соответствует такому равенству:

π 2x= −2 + 2πm, m∈ ℤ

Отсюда

π x= −4 + πm,m ∈ℤ

Эта серия корней удовлетворяет ОДЗ.

sin 2x =cos2x

Так как если бы $cos2x= 0,$ то и $sin2x$ был бы равен нулю, что невозможно, мы можем разделить обе части на $cos2x$ :

tg2x= 1

2x = π+ πk,k ∈ℤ 4

π πk x= 8 + 2 ,k ∈ℤ

Эта серия корней также удовлетворяет ОДЗ.

Ответ:

$− π + πm, m ∈ ℤ;π+ πk, k ∈ℤ. 4 8 2$

Ошибка.
Попробуйте повторить позже

Задача 26#131020Максимум баллов за задание: 7

Четырехугольник $ABCD$ вписан в окружность. Найдите все возможные значения угла $∠FEG,$ где $E,$ $F$ и $G$ — центры вписанных окружностей в треугольники $ABC,$ $BCD$ и $ABD$ соответственно.

Источники: ДВИ - 2025, вариант 255, задача 5

Подсказки к задаче

Подсказка 1

Грамотный чертеж поможет решить задачу. Рассматриваются центры вписанных окружностей разных треугольников. Какие построения могут пригодиться?

Подсказка 2

Точно! Нам нужны биссектрисы. Построим их для ∠BAC и∠BDC. Где они пересекутся? Что еще можно про них сказать?

Подсказка 3

Они пересекутся на окружности, в которую вписан ABCD, и на них расположены центры вписанных окружностей треугольников ABC и BCD. Применим лемму о трезубце, что следует из нее?

Подсказка 4

Из леммы о трезубце получим, что EX = BX = XC = FX. Проведем аналогичные действия для биссектрис ∠ACB и ∠BDA, пусть они пересекаются в точке Y. Введем обозначения для дуг AD = x и CD = y. Теперь сможем посчитать ∠XEF и ∠YEG.

Подсказка 5

XEF = 90 - x/4 и YEG = 90 - y/4. Теперь посчитаем, чему равен ∠AEC. Это угол в треугольнике между двумя биссектрисами. А чему равен ∠AEY?

Подсказка 6

Выразите его через ∠AEC. Теперь вернемся к вопросу задачи!

Показать ответ и решение

Проведем биссектрисы углов $BAC$ и $BDC.$ Они пересекутся в точке $X,$ лежащей на окружности. На проведенных биссектрисах будут лежать центры вписанных окружностей $E$ и $F.$

$PIC$

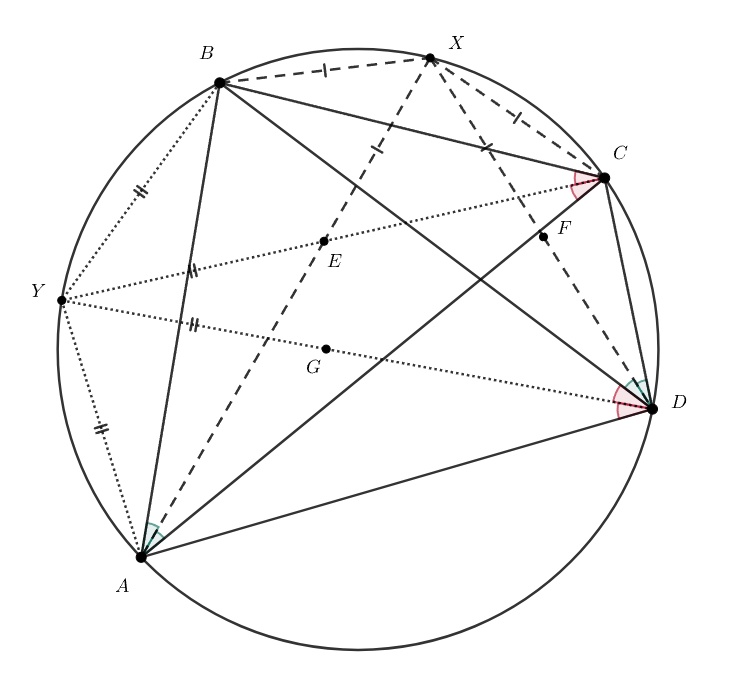
По лемме о трезубце $EX =BX =XC$ и $FX = BX = XC,$ следовательно, $EX = XF.$ Пусть биссектрисы $∠ACB$ и $∠BDA$ пересекаются в точке $Y,$ лежащей на окружности. На проведенных биссектрисах будут лежать центры вписанных окружностей $E$ и $G.$ По лемме о трезубце $AY = YB = YE =Y G.$

Рассмотрим равнобедренные треугольники $EXF$ и $GY E.$ Пусть дуга $AD = x,$ дуга $CD = y,$ тогда $x ∠AXD = 2,$ $y ∠DY C = 2.$ Поскольку $∠XEF = ∠XF E,$ а $∠EXF = x2,$ $∠XEF =90∘− x4.$ Аналогично, $y ∠YEG = 90∘− 4.$

$PIC$

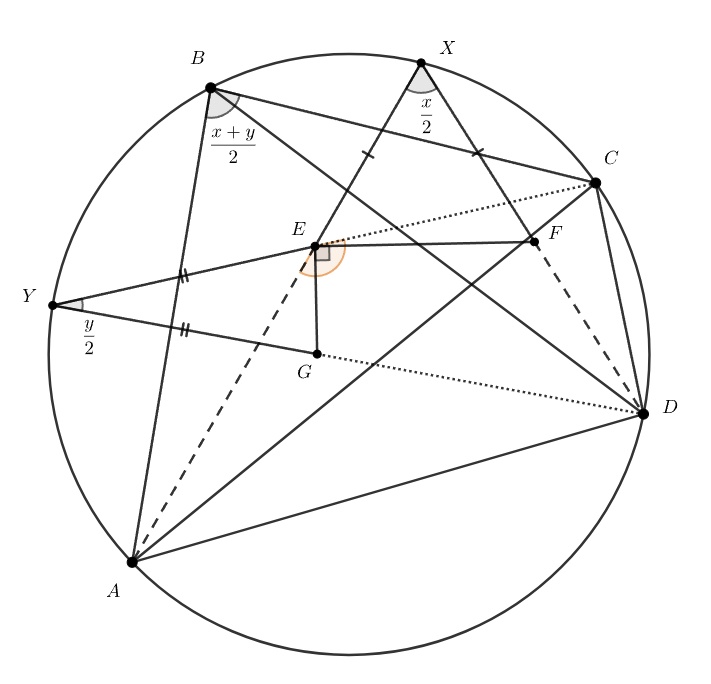
Выведем вспомогательный факт:

$PIC$

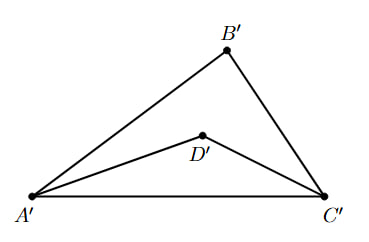
Пусть $D′$ — точка пересечения биссектрис углов $B′A′C′$ И $B′C′A ′.$ Тогда если $∠A′B′C ′ =α,$ то

′ ′ ′ ′′ ′ ∘ ∠B AC +∠B C A = 180 − α

Поскольку $A′D′$ и $C′D ′$ лежат на биссектрисах,

∠D ′A′C′+ ∠D′C′A ′ = ∠B′A′C′+-∠B′C′A′= 90∘ − α 2 2

По сумме углов в треугольнике $A′D ′C′$

′′ ′ ∘ α- ∠A D C = 90 + 2

Вернемся к исходной картинке. Рассмотрим треугольник $ABC.$ В нем $E$ — точка пересечения биссектрис. Тогда

∘ ∠B ∠AEC =90 + -2-

Кроме того,

∠AEY = 90∘− ∠2B-=90∘− x+4y

В итоге,

∠GEF = 180∘− ∠AEG − ∠XEF =180∘− ∠YEG − ∠XEF + ∠YEA = 180∘− 90∘ =90∘

Ответ:

$90∘$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 27#131022Максимум баллов за задание: 7

Положительные действительные числа $a,b,c$ удовлетворяют равенству $a2+$ $b2+$ $c2 =12.$ Найдите наибольшее возможное значение выражения

∘----- ∘----- ∘ ----- 1+ a3+ 1+ b3+ 1+ c3

Источники: ДВИ - 2025, вариант 255, задача 6

Подсказки к задаче

Подсказка 1

Нужно найти наибольшее значение выражения. Наверняка его можно как-то ограничить, ведь у нас фиксирована сумма квадратов!

Подсказка 2

Ограничивать сразу всю сумму сложно, легче ограничить каждое слагаемое отдельно и потом сложить, а еще нам известна сумма квадратов...

Подсказка 3

Как Вы думаете, можно ли применить некоторое известное неравенство для √(1 + x³)?

Подсказка 4

Разложим на множители: 1 + x³ = (1 + x)⋅(1 - x + x²).

Подсказка 5

Воспользуйтесь неравенством о средних.

Подсказка 6

Нам известна сумма квадратов, можем ее подставить! Остается только подобрать пример.

Показать ответ и решение

Докажем, что для любого положительного действительного числа $x$ выполняется неравенство:

∘ ----3 1 2 1+ x ≤ 2x + 1

Так как обе части неравенства положительны, мы можем возвести их в квадрат:

( )2 1+x3 ≤ 1x2+1 2

1 +x3 ≤ 1x4+ x2+ 1 4

2 2 0 ≤x (x− 2)

Это неравенство всегда верно. Равенство достигается при $x =2.$

Теперь применим доказанное неравенство к каждому слагаемому искомого выражения:

∘----- ∘----- ∘ ----- ( ) ( ) ( ) 1+ a3+ 1+ b3+ 1+ c3 ≤ 1a2+ 1 + 1b2+ 1 + 1c2+1 2 2 2

∘1+-a3+ ∘1+-b3+∘1-+-c3 ≤ 1(a2+ b2+ c2)+ 3 2

По условию $a2+ b2+ c2 = 12,$ подставим это значение:

∘----3 ∘----3 ∘ ----3 1 1+ a + 1+ b + 1+ c ≤ 2 ⋅12+ 3= 9

Мы показали, что значение выражения не превышает 9. Осталось показать, что это значение достигается. Равенство в нашем неравенстве достигается тогда и только тогда, когда оно достигается для каждого из трех слагаемых, то есть при $a= 2,$ $b=2,$ и $c= 2.$ Проверим, удовлетворяет ли этот набор чисел исходному условию:

a2 +b2+ c2 =22+ 22+22 =4+ 4+ 4= 12

Условие выполняется. Таким образом, наибольшее возможное значение выражения равно 9.

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 28#131023Максимум баллов за задание: 7

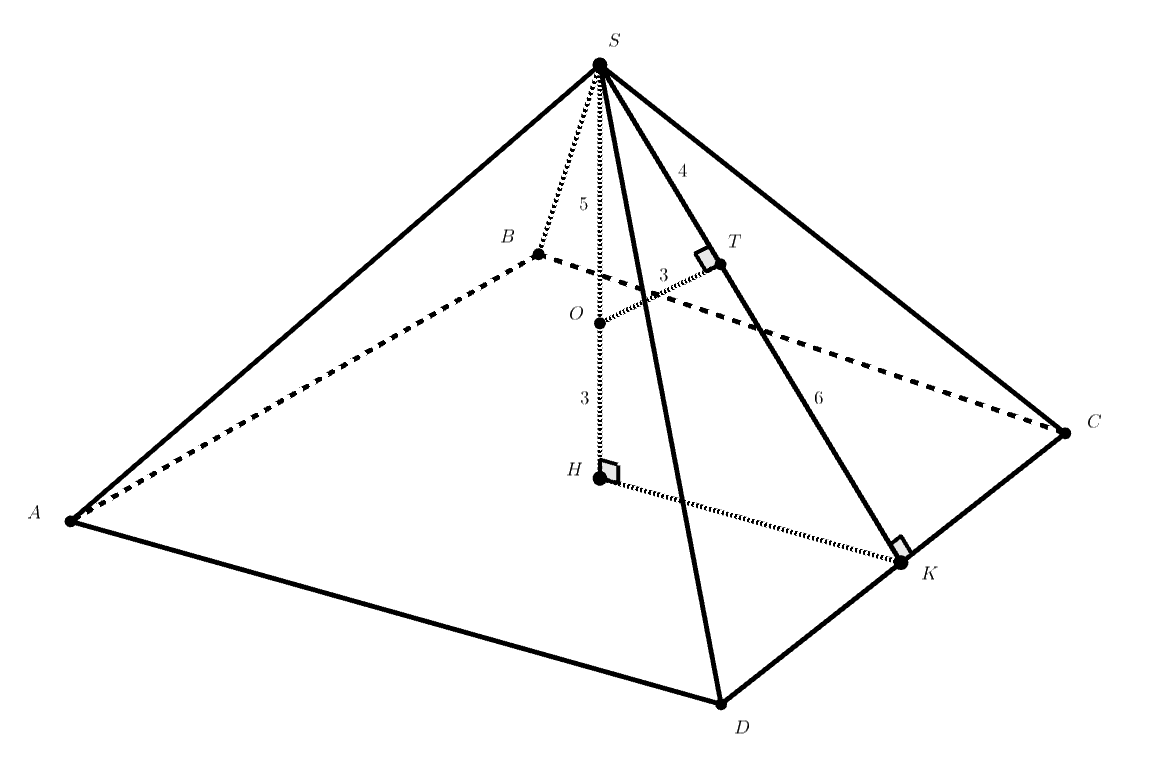
Дана четырехугольная пирамида $ABCDS$ с высотой $SH = 8.$ Сфера радиуса 3 касается всех граней пирамиды, причем основания $ABCD$ эта сфера касается в точке $H$ основания высоты. Найдите периметр четырехугольника $ABCD,$ если известно, что его площадь равна 144.

Источники: ДВИ - 2025, вариант 255, задача 7

Подсказки к задаче

Подсказка 1

Выразим объем четырехугольной пирамиды двумя способами, отсюда найдем площадь полной поверхности.

Подсказка 2

Мы знаем площадь полной поверхности, из чего она состоит? Как можно посчитать площадь треугольников?

Подсказка 3

Попробуем дойти до высоты треугольника CSD. Проведем перпендикуляр OT из центра вписанной сферы к грани CSD, K — точка пересечения ST и CD. Можем ли мы теперь узнать высоту CSD?

Подсказка 4

Можем! Выражаем отрезки, пользуясь подобием треугольников, применяем теорему о трех перпендикулярах и получаем, что SK перпендикулярно CD. Что будет, если выполнить аналогичные действия для других граней?

Подсказка 5

Высоты в гранях равны. Используем площадь полной поверхности и выражаем периметр четырехугольника.

Показать ответ и решение

$PIC$

С одной стороны,

VABCDS = 1 ⋅SABCD ⋅SH 3

С другой, если $r$ — радиус вписанной сферы, $Sпп$ — площадь полной поверхности, то

VABCDS = 1 ⋅r⋅Sпп 3

Тогда

1 1 3 ⋅144⋅8 = 3 ⋅3⋅Sпп

Sпп = 48⋅8

Пусть $O$ — центр вписанной сферы, $OT$ — перпендикуляр к грани $CSD,$ прямая $ST$ пересекает $CD$ в точке $K.$ Так как $SH = 8,$ $OH = 3,$ то $SO = 5,$ а также $OT = 3,$ следовательно, в треугольнике $SOT$ $ST = 4.$ Кроме того, $△SOT$ подобен $△SHK,$ следовательно,

SO ST SK-= SH-

5 4 SK- = 8

SK = 10

По теореме о трех перпендикулярах, $SK ⊥CD.$ Заметим, что если мы будем опускать высоты на остальные грани из точки $O,$ каждый раз будем получать те же самые подобные треугольники, следовательно, высоты в гранях равны. Тогда

Sпп = 48⋅8= SABCD +SASB +SBSC + SCSD+ SDSA =

= 144+ 1 ⋅AB⋅10+ 1⋅BC ⋅10+ 1⋅CD ⋅10+ 1⋅DA ⋅10 = 2 2 2 2

= 144 + 1 ⋅10 ⋅PABCD 2

PABCD = 48

Ответ: 48

Ошибка.
Попробуйте повторить позже

Задача 29#132595Максимум баллов за задание: 7

Какое из следующих двух чисел больше: $∘ 20- 13 7 + 3$ или 6?

Источники: ДВИ - 2025, вариант 256, задача 1

Подсказки к задаче

Подсказка 1

Если мы хотим сравнить 2 положительных числа, то можно посмотреть на их квадраты. А как это сделать более удобно в нашей задаче? Не хотелось бы возводить сумму в квадрат...

Подсказка 2

Вычтите из обоих чисел 13/3. Останется только сравнить две дроби, например, приведя их к общему знаменателю.

Показать ответ и решение

Вычтем из обоих чисел $13 3$ и сравним $∘ 20- 7$ с $5 3.$

Возведем оба числа в квадрат, тогда если, например, квадрат первого числа окажется больше квадрата второго, то можно сделать вывод, что первое число больше второго, так как они положительные. Получим $20 7-$ и $25 9-.$ Осталось лишь привести их к общему знаменателю:

20 20⋅9 180 7-= -7⋅9 =-56

25= 25⋅7 = 175 9 9⋅7 56

Квадрат первого числа больше, следовательно, первое число больше.

Ответ:

Первое число больше

Ошибка.
Попробуйте повторить позже

Задача 30#132597Максимум баллов за задание: 7

Положительные действительные числа $a$ и $b$ удовлетворяют равенствам $a3 = a+1$ и $b6 = b+ 3a.$

Определите, какое из чисел $a$ и $b$ больше другого.

Источники: ДВИ - 2025, вариант 256, задача 2

Показать ответ и решение

Пусть

3 f(a)= a − a− 1 =0

Посчитаем производную

′ 2 f(a)= 3a − 1

Точки экстремума функции — это $1√- 3$ и $− 1√-. 3$ Рассмотрим промежутки возрастания и убывания:

$−1√31√3↗↘↗$

Заметим, что

f(0)< 0 и f(1)< 0

По условию, $a >0,$ следовательно, $a> 1,$ так как в точке $a$ функция $f$ должна обращаться в 0.

Пусть

6 g(b)= b− b− 3a= 0

Посчитаем производную

g′(b)= 6b5− 1

Точки экстремума функции — это $15√-- 6$ и $− √15. 6$ Рассмотрим промежутки возрастания и убывания:

$−15√615√6↗↘↗$

Заметим, что

g(0)< 0 и g(1)< 0

По условию, $b> 0,$ следовательно, $b> 1,$ так как в точке $b$ функция $g$ должна обращаться в 0.

Нам даны равенства $a3 = a+ 1$ и $b6 = b+3a.$ Возведем первое в квадрат:

6 2 a =a + 2a+ 1

Заметим, что

a2+ 2a+1 − 4a= a2− 2a +1 =(a− 1)2 ≥ 0

Так как $a> 1,$

(a− 1)2 > 0

Следовательно,

a6 =a2+ 2a+ 1> 4a

Получим, что

6 6 a − b >4a− b− 3a =a − b

6 6 a − a> b − b

Рассмотрим функцию

h(x)= x6− x

Она возрастает при $x> 1,$ следовательно, так как $a > 1$ и $b >1,$

h(a)> h(b)

a> b

Ответ:

$a >b$

Ошибка.
Попробуйте повторить позже

Задача 31#132599Максимум баллов за задание: 7

Решите неравенство

3 2 5 log32 x2 +log23 x3 ≤ 6 ⋅x ⋅log6 x

Источники: ДВИ - 2025, вариант 256, задача 3

Подсказки к задаче

Подсказка 1

Для начала стоит записать ОДЗ.

Подсказка 2

Получим, что x > 0. Попробуйте привести логарифмы к одному основанию.

Подсказка 3

Например, нам может помочь следующее свойство: logₐb = logₕb / logₕa.

Подсказка 4

Можно взять h = 6.

Подсказка 5

Примените метод рационализации.

Показать ответ и решение

На ОДЗ: $x >0.$

3 2 5 2 ⋅log32 x− 3 ⋅log32 x≤ 6 ⋅x⋅log6x

5 5 6 ⋅log32 x≤ 6 ⋅x⋅log6x

log3 x≤ x⋅log6x 2

x⋅log6x− log6x-≥ 0 log6 32

log6x ⋅(x− log36)≥ 0 2

По методу рационализации

(6− 1)⋅(x − 1)⋅(x − log36)≥0 2

(x − 1)⋅(x − log36)≥0 2

$x1lo++g36 2$

[ ) x∈(−∞; 1]∪ log32 6;+∞

На пересечении с ОДЗ получим

[ ) x∈(0;1]∪ log32 6;+∞

Ответ:

$(0;1]∪ [log 6;+∞) 32$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 32#132615Максимум баллов за задание: 7

Решите уравнение

sin2x− cos2x =tgx

Источники: ДВИ - 2025, вариант 256, задача 4

Показать ответ и решение

На ОДЗ $cosx⁄= 0,$ поскольку $tgx$ определён корректно, поэтому

2 sinx- 2sinxcosx− 2cos x+ 1= cosx

1 2cosx(sinx − cosx)− cosx(sinx− cosx)= 0

( ) 2cosx − -1-- (sinx − cosx)=0 cosx

⌊ 2cosx− -1--= 0 |⌈ cosx sin x− cosx= 0

Так как на ОДЗ $cosx⁄= 0,$ домножим на него первое равенство системы и поделим второе:

[ 2cos2x− 1= 0 tgx= 1

[ cos2x= 0 tgx= 1

⌊ π πk || x =-4 + 2-,k∈ ℤ ⌈ x = π + πn,n ∈ℤ 4

π πk x= 4 +-2 ,k ∈ℤ

Ответ:

$π + πk, 4 2$ $k∈ ℤ$

Ошибка.
Попробуйте повторить позже

Задача 33#132617Максимум баллов за задание: 7

На сторонах $AB$ и $AC$ остроугольного треугольника $ABC$ как на диаметрах построены окружности $Ω 1$ и $Ω 2$ соответственно. Через точку $D$ пересечения этих окружностей (отличную от $A),$ проведена прямая, пересекающая $Ω1$ и $Ω2$ в точках $E$ и $F$ соответственно, причем $E$ и $F$ лежат по одну сторону от $AD$ (и отличны от $D ).$ Расстояние от $A$ до середины $M$ стороны $BC$ равно 3, расстояние от $A$ до середины $N$ отрезка $EF$ равно 2. Найдите $MN.$

Источники: ДВИ - 2025, вариант 256, задача 5

Подсказки к задаче

Подсказка 1

Для начала рассмотрим точку D. Где она лежит?

Подсказка 2

Верно, точка D — это основание высоты из точки A. Теперь внимательно посмотрим на чертёж: нам даны две окружности, значит, где-то точно есть вписанный четырёхугольник...

Подсказка 3

Например, такими являются ABED и AFCD. Воспользуйтесь свойствами вписанных четырёхугольников, чтобы найти равные уголочки. Что можно сказать про треугольники ABC и AEF?

Подсказка 4

Да, эти треугольники подобны! Теперь попробуйте доказать, что четырёхугольник AMND — вписанный, используя равенство некоторых углов.

Показать ответ и решение

$PIC$

Точка $D,$ как можно видеть, основание высоты из $A.$ Докажем, что $A,$ $M,$ $N,$ $D$ лежат на одной окружности, для этого мы проверим, что $∠NDM = ∠MAN.$ Так как точки $A,$ $B,$ $E,$ $D$ лежат на одной окружности, то

∠AED = 180∘ − ∠ABC

Откуда так, как $D,$ $E,$ $F$ на одной прямой $∠FEA = ∠ABC.$ Аналогично $∠EF A =∠BAC.$

Из этих двух равенств следует, что $△ABC$ подобен $△AEF.$ А так как $AN$ и $AM$ медианы в подобных треугольниках, то $∠EAN =∠BAM.$ Откуда сразу следует, что

∠MAN =∠NAE +∠EAM = ∠BAM + ∠MAE =∠BAE

Снова воспользуемся тем, что точки $A,$ $B,$ $E,$ $D$ лежат на одной окружности:

∘ ∠MAN = ∠BAE = 180 − ∠BDE =∠NDM

Значит, мы доказали, что $A,$ $M,$ $N,$ $D$ лежат на одной окружности.

Дальше пользуемся этим и получаем,что $∠ANM =∠ADM = 90∘.$ Поэтому применяем теорему Пифагора:

∘---2-----2 √- MN = AM − AN = 5

Ответ:

$√5$

Ошибка.
Попробуйте повторить позже

Задача 34#132665Максимум баллов за задание: 7

Положительные действительные числа $a,$ $b,$ $c$ удовлетворяют равенству $a +b+ c= 3.$ Найдите наибольшее возможное значение выражения

(1+ a)2 (1 +b)2 (1 +c)2 ----1-+ ---1--+ ---1-- a + b b+ c c+a

Источники: ДВИ - 2025, вариант 256, задача 6

Подсказки к задаче

Подсказка 1

Заметим, что нам дана сумма 3 похожих дробей. Как этим можно воспользоваться?

Подсказка 2

Давайте попробуем отдельно оценить одну из дробей, тогда для оценки суммы нам останется лишь умножить ее на 3!

Подсказка 3

Оценка будет иметь следующий вид: (a + b)² / (a + 1/b) ∨ X. Это равносильно (a + b)² ∨ X⋅(a + 1/b). Раскройте скобки в левой части и попробуйте подобрать какое-то X.

Подсказка 4

Скорее всего, что-то получится, если X также будет скобкой, зависящей от a и b.

Подсказка 5

А если взять X = (a + b)?

Подсказка 6

Попробуйте увидеть квадрат разности.

Подсказка 7

Воспользуйтесь тем, что a + b + c ‎ = 3. Останется лишь подобрать пример.

Показать ответ и решение

Докажем, что

(1-+a)2 1 ≤ a+ b a+ b

Для этого преобразуем неравенство

2 ( 1) (1 +a) ≤ (a+ b) a+ b

1+ 2a +a2 ≤ a2+ a+ ab+1 b

2≤ 1 +b b

2b≤ 1+ b2

b2− 2b+ 1≥ 0

2 (b− 1) ≥ 0

Аналогичные утверждения справедливы и для остальных дробей. Тогда

S ≤ (a +b)+ (b+ c)+(a+ c)= 2(a+b+ c)

По условию, $a +b+ c= 3,$ следовательно,

S ≤ 6

Равенство выполняется при

a= b= c=1

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 35#132668Максимум баллов за задание: 7

Дан правильный тетраэдр $ABCD$ с ребром $2√3.$ Найдите площадь сечения этого тетраэдра плоскостью, касающейся сферы, вписанной в тетраэдр, и параллельной ребрам $AB$ и $CD.$

Источники: ДВИ - 2025, вариант 256, задача 7

Показать ответ и решение

Для начала заметим, что центр вписанной сферы — это точка пересечения всех высот тетраэдра. Проведём эти высоты и назовём их $AH , 1$ $BH2,$ $CH3,$ $DH4.$ Точки $H1,$ $H2,$ $H3$ и $H4,$ в свою очередь, будут являться точками касания и представлять собой точки пересечения высот правильных треугольников, являющихся гранями тетраэдра. Также для всех этих граней сразу найдем длину отрезка, являющегося медианой, высотой и биссектрисой:

∘ -√------√--- √ ----- m = (2 3)2− ( 3)2 = 12− 3 =3

Теперь рассмотрим плоскость из условия. Видно, что она будет представлять из себя параллелограмм, который назовём $W XY Z,$ где $W X$ – отрезок, параллельный ребру $CD$ на грани $BCD,$ а $Y Z$ — отрезок, параллельный ребру $CD$ на грани $ACD.$ Более того, несложно заметить, что этот параллелограмм является прямоугольником, так как $DC$ перпендикулярно $AB$ — это доказывается, если рассмотреть проекцию $DC$ на основание тетраэдра $ABC$ и заметить, что эта проекция перпендикулярна $AB$ (основание и высота треугольника $ABC$ ).

Далее нам необходимо найти радиус вписанной сферы. Для этого воспользуемся тем, что ее центр является точкой пересечения высот тетраэдра, которые в силу его правильности являются и медианами. А так как в треугольной пирамиде медианы делятся точкой пересечения в отношении $3:1,$ то получаем, что радиус сферы равен $14$ высоты тетраэдра. Воспользуемся формулой для высоты правильного тетраэдра и получим, что она равна:

√-√- √- h= 2-3-6-= 6-2= 2√2 3 3

То есть радиус вписанной сферы:

√- √- r= 2-2 = -2- 4 2

Теперь заметим, что в силу построения наше сечение касается сферы в точке, лежащей на прямой, соединяющей середины $AB$ и $CD.$ Пусть середина $CD$ — $K,$ а точка касания — $P.$ При этом эта же прямая проходит через центр сферы. Обозначим центр сферы за $O$ и проведем на грани $ABD$ высоту $DH,$ которая будет являться также биссектрисой и медианой. После этого рассмотрим прямоугольный треугольник $OH4H.$

Величину $OH4$ мы знаем — это радиус найденной сферы. Чтобы найти $H4H$ заметим, что $H4$ — точка пересечения медиан треугольника $ABC,$ а $CH$ как раз и является этой медианой. Тогда:

√----- H4H = CH- = -12−-3= 1 3 3

Отсюда можем найти $OH:$

----- ∘ 2 √6- OH = 1+ 4 = 2

Отсюда получается, что

√6− √2 PH = ---2---

Теперь найдем $KH:$

∘ ---------- KH = CH2− CK2 = √9−-3= √6

Обозначим на прямых $DH$ и $CH$ точки пересечения с нашим сечением: $Q$ и $S.$ Далее из подобия треугольников $QSH$ и $CDH$ получаем, что:

-QS PH- CD = KH

QS √6 − √2 2√3-= --2√6--

QS = √3− 1= WX

Из этого же подобия:

-SH = QS- CH CD

√- √- SH-= -6−√--2- 3 2 6

√- SH = 3-−-3 2

Аналогично из подобия треугольников $ABC$ и $W ZC$ получаем, что:

-CS = WZ- CH AB

3− √3 3−---2--- W-Z 3 = 2√3-

√ - √- W Z = 2-3(3+--3) 6

√- W Z = 3+ 1

Тогда можем найти площадь сечения как площадь прямоугольника $W XYZ:$

SWXY Z =W Z ⋅W X = (√3-+1)(√3− 1)=3− 1= 2

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 36#132896Максимум баллов за задание: 7

Известно, что $x:y =9 :7.$ Найдите $x-+y. x − y$

Источники: ДВИ - 2025, вариант 251, задача 1

Подсказки к задаче

Подсказка 1

Выразим x через y и подставим в выражение, значение которого необходимо найти.

Показать ответ и решение

Так как

x 9 9 y = 7 и x= 7 ⋅y,

получаем, что

9 16- x+y-= 79 ⋅y+-y-= 72-⋅y= 8 x− y 7 ⋅y− y 7 ⋅y

Ответ: 8

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 37#132897Максимум баллов за задание: 7

Дана последовательность $a,a ,a... 1 2 3$ действительных чисел, удовлетворяющих при каждом натуральном $n$ равенству

5−-an an+1 = 4

Пусть $Sn$ обозначает сумму первых $n$ членов этой последовательности: $Sn = a1 +...+ an.$ Известно, что $a1 = 11.$ Найдите наименьшее значение $n,$ при котором выполняется неравенство

1 |Sn− n− 8|< 1000

Источники: ДВИ - 2025, вариант 251, задача 2

Подсказки к задаче

Подсказка 1

Попробуйте вычислить несколько первых членов последовательности.

Подсказка 2

Подумайте, имеет ли полученная последовательность какие-нибудь примечательные свойства?

Подсказка 3

Это геометрическая прогрессия! Попробуйте понять, через какую формулу можно найти ее n-ый член.

Подсказка 4

aₙ = 1 + 10 ⋅ (-1/4)ⁿ⁻¹.

Подсказка 5

Осталось лишь найти по формуле сумму геометрической прогрессии и подобрать n.

Показать ответ и решение

Заметим, что искомому рекуррентному соотношению удовлетворяет данная формула для $n$ -го члена последовательности:

( 1)n−1 an =1+ 10 − 4

Покажем это, подставив формулу в соотношение:

( ) ( )n 5− 1− 10 − 1 n− 1 ( )n−1 ( )n 1+ 10 − 1 = ----------4-----= 1+ (−1)⋅ 1 ⋅10 − 1 = 1+ 10 − 1 4 4 4 4 4

По формуле суммы геометрической прогрессии найдем сумму:

∑n ( ( 1)k− 1) n∑ ( 1)k−1 ( ( 1)n) ( 1)n Sn = 1+ 10 −4 = n+ 10 −4 = n+ 8 1 − − 4 =n +8 − 8 − 4 k=1 k=1

Теперь рассмотрим выражение $|Sn− n− 8|:$

| ( ) | | ( ) | |( ) | |S − n− 8|= ||n+ 8− 8 − 1 n − n − 8||= ||− 8 − 1 n||=8|| − 1 n||= 8 n | 4 | | 4 | | 4 | 4n

Найдем наименьшее $n,$ для которого выполняется неравенство:

8n-< -1-- 4 1000

8000 <4n

Проверим степени четверки: $45 = 1024,$ $46 =4096,$ $47 =16384.$ Неравенство $4n >8000$ впервые выполняется при $n =7.$

Ответ: 7

Ошибка.
Попробуйте повторить позже

Задача 38#132898Максимум баллов за задание: 7

Решите неравенство

∘------2------- 2 1+ log9(3x +8x +6)> log3(3x + 8x+6)

Источники: ДВИ - 2025, вариант 251, задача 3

Подсказки к задаче

Подсказка 1

Замена так и напрашивается. Не забудьте проверить ОДЗ!

Подсказка 2

Теперь перед нами довольно простое неравенство, решите его любым удобным способом.

Подсказка 3

Например, можно рассмотреть 2 случая: когда часть без корня больше 0 и когда она меньше.

Подсказка 4

Финишная прямая, осталось сделать обратную замену и решить полученное простое неравенство.

Показать ответ и решение

Проверим ОДЗ:

2 3x + 8x+ 6> 0

Так как

D = 82− 4 ⋅3 ⋅6 =64− 72= −8< 0

Сделаем замену $t= log3(3x2+ 8x+6),$ получим:

∘ -- 1+ t> t 2

Это неравенство равносильно совокупности двух систем:

⌊ (| t− 1< 0 || { || |( t ≥ 0 ||| ( 2 || |{ t− 1≥ 0 ⌈ |( t > (t− 1)2 2

Решим первую систему:

{ t< 1 t≥ 0

t ∈[0;1)

Решим вторую систему:

{ t≥ 1 2 t> 2(t − 2t+ 1)

{ t≥ 1 2t2− 5t+ 2< 0

(| t≥ 1 { ( ) |( t∈ 1;2 2

Объединяя решения обеих систем, получаем:

t ∈[0;2)

Сделаем обратную замену:

0≤ log3(3x2+ 8x+ 6)< 2

Это равносильно системе неравенств:

{ log3(3x2+ 8x+ 6) ≥0 log3(3x2+ 8x+ 6) <2

{ 3x2+ 8x +6≥ 1 3x2+ 8x +6< 9

{ 3x2+ 8x +5≥ 0 3x2+ 8x − 3< 0

( ( ) |||{ x∈ −∞; − 5 ∪[−1;+∞) ( )3 |||( x∈ −3;1 3

Пересекая эти два решения, получаем итоговый ответ:

( 5) [ 1) x∈ −3;3 ∪ −1;3

Ответ:

$(−3;5)∪ [−1;1) 3 3$

Ошибка.
Попробуйте повторить позже

Задача 39#132899Максимум баллов за задание: 7

Решите уравнение

√- sin2x+3cosx= 3(1+ cos2x+ sinx)

Источники: ДВИ - 2025, вариант 251, задача 4

Подсказки к задаче

Подсказка 1

Нам даны тригонометрические функции от разных аргументов. Как это можно изменить?

Подсказка 2

Используем формулы синуса и косинуса двойного угла. Слева и справа что-то получилось, перенесем в одну сторону и раскроем скобки.

Подсказка 3

Дошли до уравнения: 2sin(x)cos(x) + 3cos(x) - 2√3cos²(x) - √3sin(x) = 0. Можно ли его разложить на множители?

Подсказка 4

Вынесем общий множитель у первого и четвертого слагаемых и у второго и третьего слагаемых.

Подсказка 5

Осталось решить совокупность уравнений, не забывая про осторожность с делением на 0!

Показать ответ и решение

Применив формулы синуса и косинуса двойного угла, получим:

√- 2 2sinxcosx +3cosx= 3(2cos x+ sinx)

Перенесем все члены в левую часть и сгруппируем:

√ - 2 √- 2sinxcosx +3cosx− 2 3cos x− 3sinx= 0

(2sinxcosx− √3sinx)+ (3 cosx− 2√3cos2x)= 0

sinx(2cosx− √3)− √3cosx(2cosx− √3-)=0

Вынесем общий множитель $√- (2cosx− 3)$ :

(2cosx− √3)(sinx− √3cosx)= 0

Это уравнение равносильно совокупности двух уравнений:

⌊ √- | cosx= -3- ⌈ √2 sin x= 3cosx

Решим первое уравнение:

√- cosx= -32-

x =± π+ 2πk, k∈ ℤ 6

Теперь решим второе уравнение:

√ - sinx = 3cosx

Заметим, что если $cosx =0,$ то из уравнения следует, что и $sinx =0,$ что невозможно. Следовательно, $cosx⁄= 0,$ и мы можем разделить обе части уравнения на $cosx$ :

tgx= √3

x = π + πk, k∈ ℤ 3

Ответ:

$± π + 2πk, 6$ $π+ πk, 3$ $k∈ ℤ$

Ошибка.
Попробуйте повторить позже

Задача 40#132900Максимум баллов за задание: 7

В треугольнике $ABC$ проведена медиана $AD.$ Известно, что $AD :BC =√3-:2$ и что $∠BAC = 45∘.$ Найдите $∠BMC,$ где $M$ — точка пересечения медиан.

Источники: ДВИ - 2025, вариант 251, задача 5

Подсказки к задаче

Подсказка 1

У нас есть отношение отрезков, можем ли через него выразить что-то еще?

Подсказка 2

Если BC = 2x, то мы можем выразить AD и DM через x. Кажется, обнаружены подобные треугольники, какие?

Подсказка 3

△ADB∼△BDM, из подобия получаем равные углы у этих треугольников. Какие тогда треугольники тоже будут подобны?

Подсказка 4

△ADC∼△CDM. Получили 2 пары равных углов: ∠BMD=∠DBA, ∠DMC=∠DCA. Осталось ими воспользоваться и найти искомый угол!

Показать ответ и решение

Введём обозначение $AD =√3x,$ тогда $BC = 2x$ из условия на отношения сторон.

$PIC$

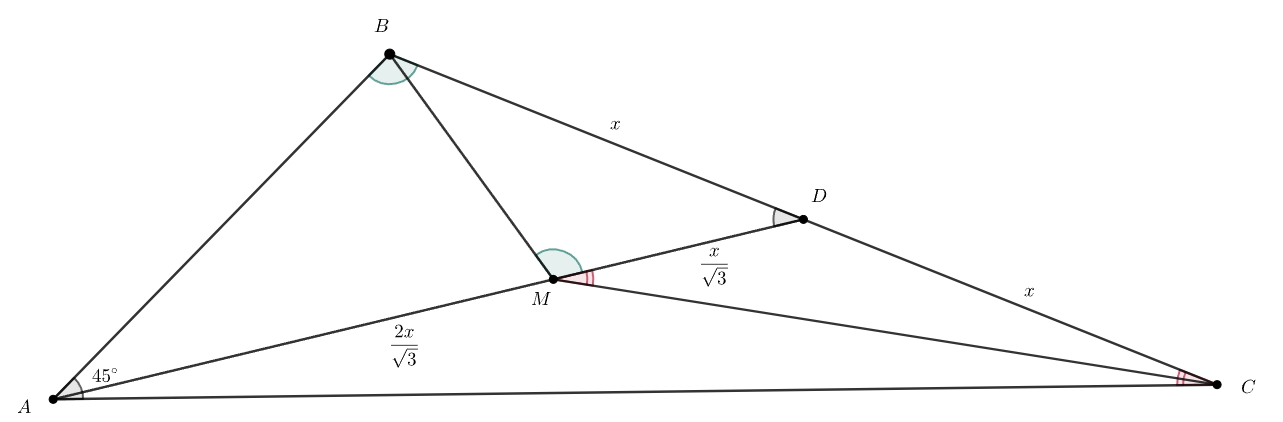
Так как $AD$ — медиана, то $BD = x,$ а так как $M$ — точка пересечения медиан, то

x DM = √3-

Заметим два подобных треугольника $△ADB$ и $△BDM,$ так как $∠D$ — общий и $√ - AD :DB = BD :DM = 3.$ Из этого подобия следует, что $∠BMD =∠DBA,$ аналогично для вершины $C,$ получаем, что $∠DMC = ∠DCA.$

Осталось использовать эти два равенства вместе:

∠BMC = ∠BMD +∠CMD = ∠DBA + ∠DCA = 180∘ − ∠BAC =135∘

Ответ:

$135∘$