Антипараллельность
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
Из точек
и
опустили перпендикуляры на прямые
и
Докажите, что прямая, проходящая через основания этих перпендикуляров, параллельна
Обозначим основания перпендикуляров через и
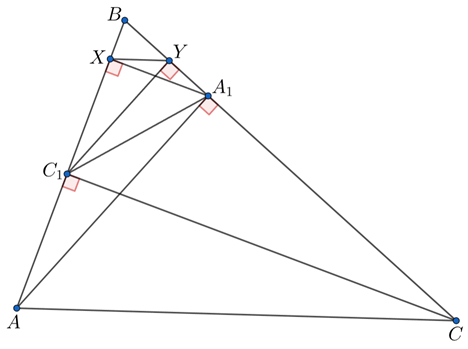
Заметим, что четырёхугольники и
вписанные. Значит,
Это и даёт
параллельность.
Ошибка.
Попробуйте повторить позже
и
— высоты треугольника
.
и
— высоты треугольника
Докажите, что
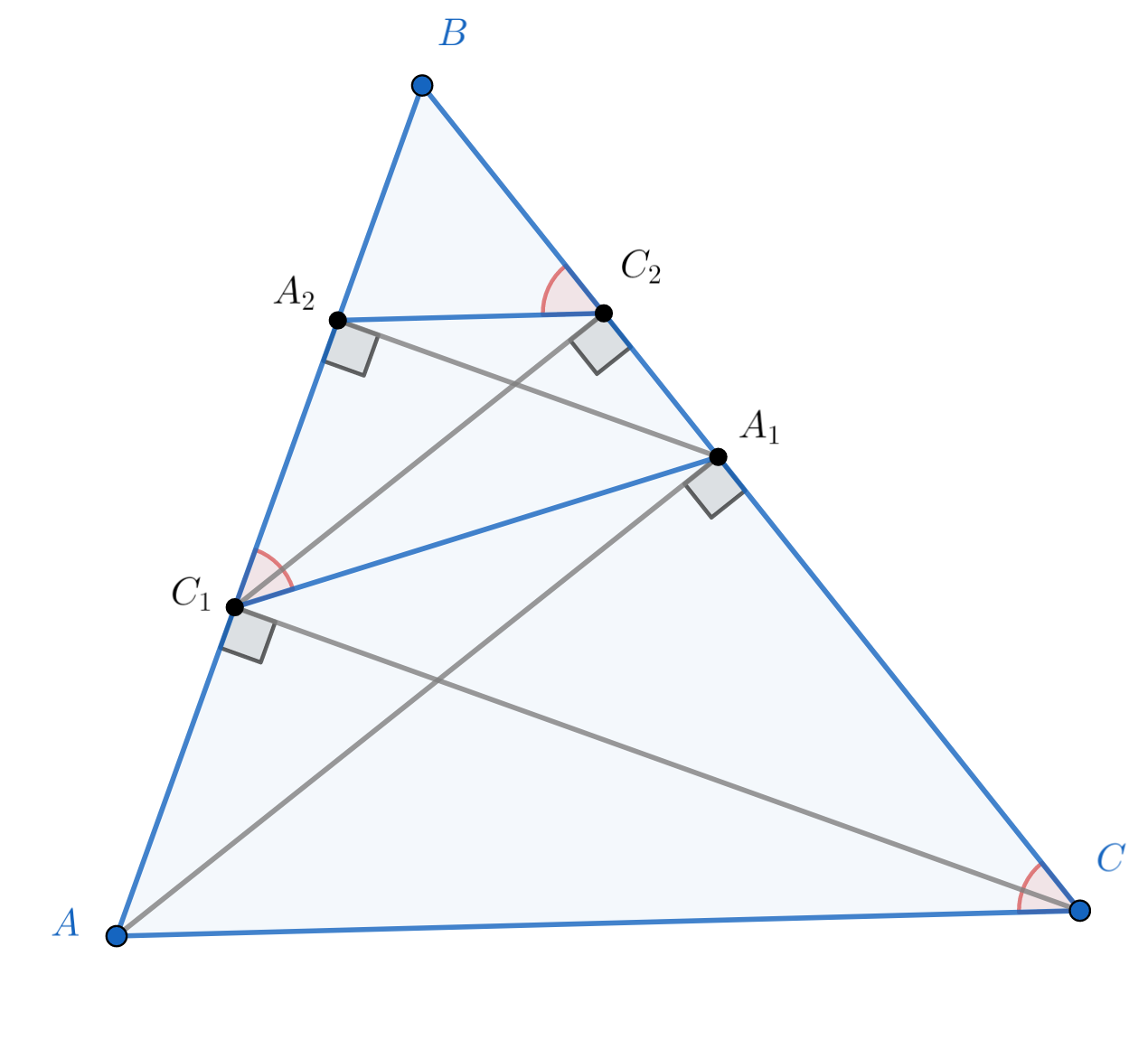
Заметим, что и
равны и опираются на один отрезок
то есть четырёхугольник
вписанный. Отсюда
Аналогично, четырёхугольник вписанный, так как
Отсюда
Итак, — соответственные углы при прямых
и
и секущей
, отсюда
Ошибка.
Попробуйте повторить позже
Докажите, что все прямые, антипараллельные данной прямой относительно данного угла
параллельны между собой, а также
параллельны прямой
симметричной
относительно биссектрисы
Пусть прямая антипараллельна прямой
относительно
прямая
пересекает стороны угла в точках
и
прямая
— в
точках
и
прямая
— в точках
и
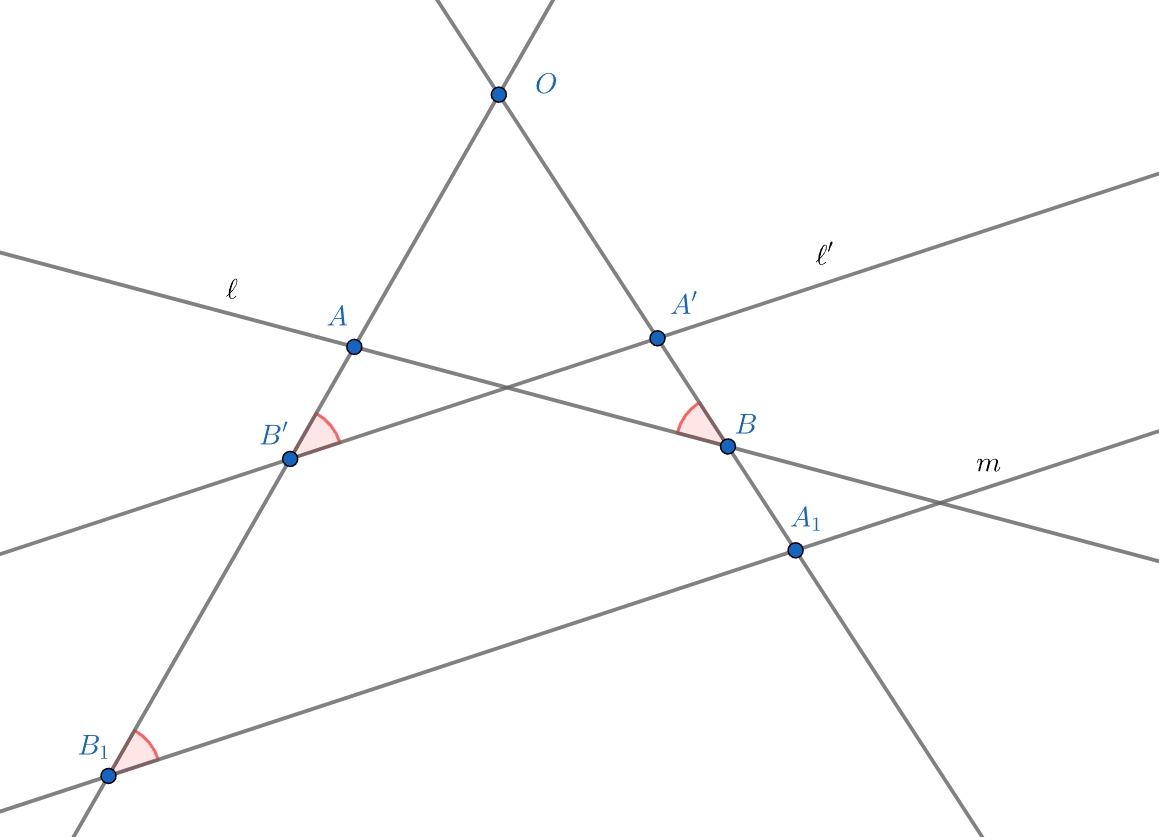
В силу антипараллельности значит, все прямые, антипараллельные
образуют с
равные углы, следовательно,
они все параллельны по равенству соответствующих или накрест лежащих углов при секущей
По свойству симметрии относительно биссектрисы получаем
Следовательно,
параллельна
значит, и всем
прямым, антипараллельным
Ошибка.
Попробуйте повторить позже
В треугольнике отрезок
антипараллелен стороне
Докажите, что
где
— центр описанной
окружности.
Пусть так как
и
— антипараллельные относительно угла
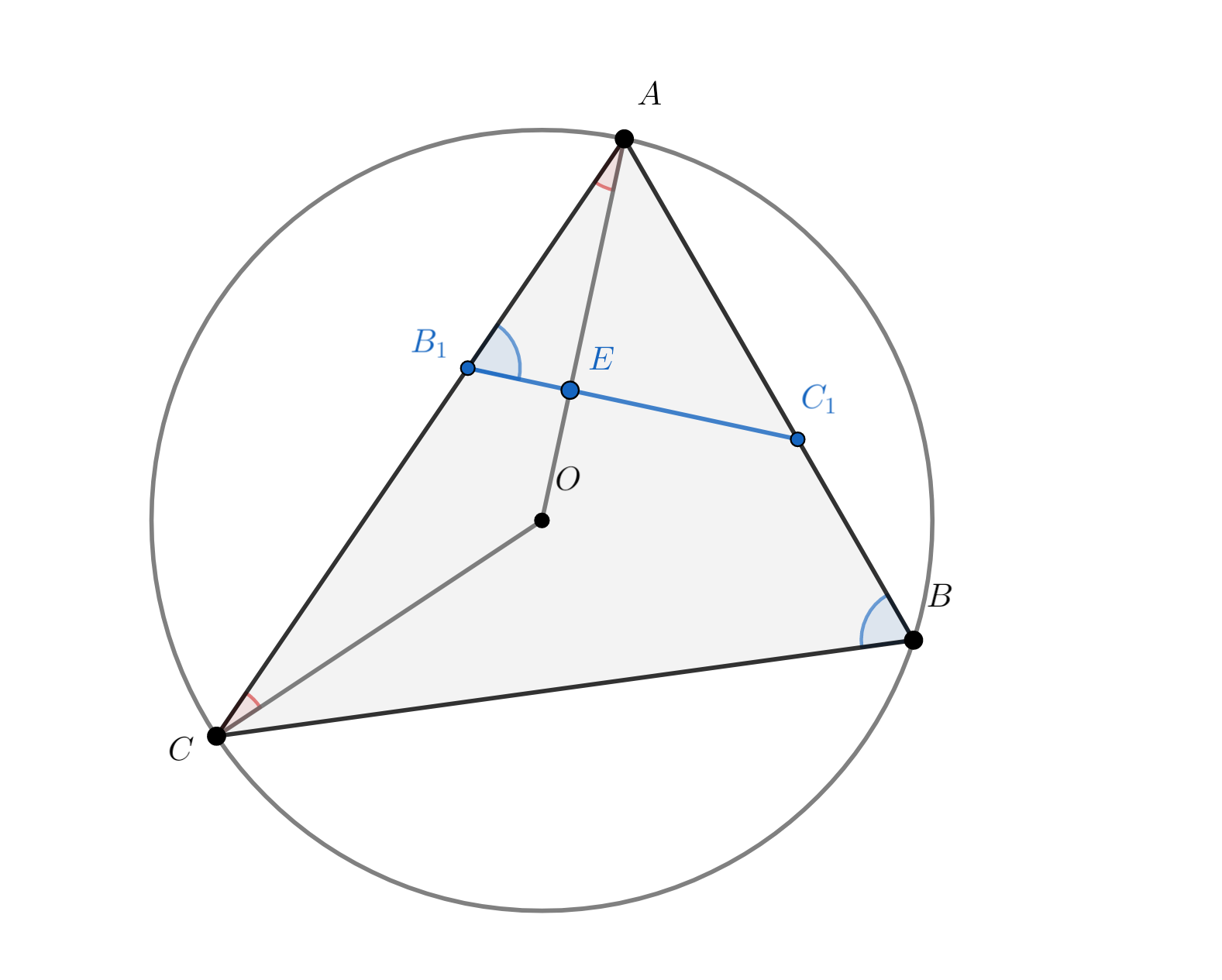
Заметим, что как центральный, опирающийся на дугу
Так как
— радиусы, то треугольник
— равнобедренный, отсюда
Пусть пересекает
в точке
Тогда
То есть
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник ;
,
,
— его высоты,
— центр описанной окружности. Докажите, что касательная в
точке
к описанной окружности параллельна прямой
, а
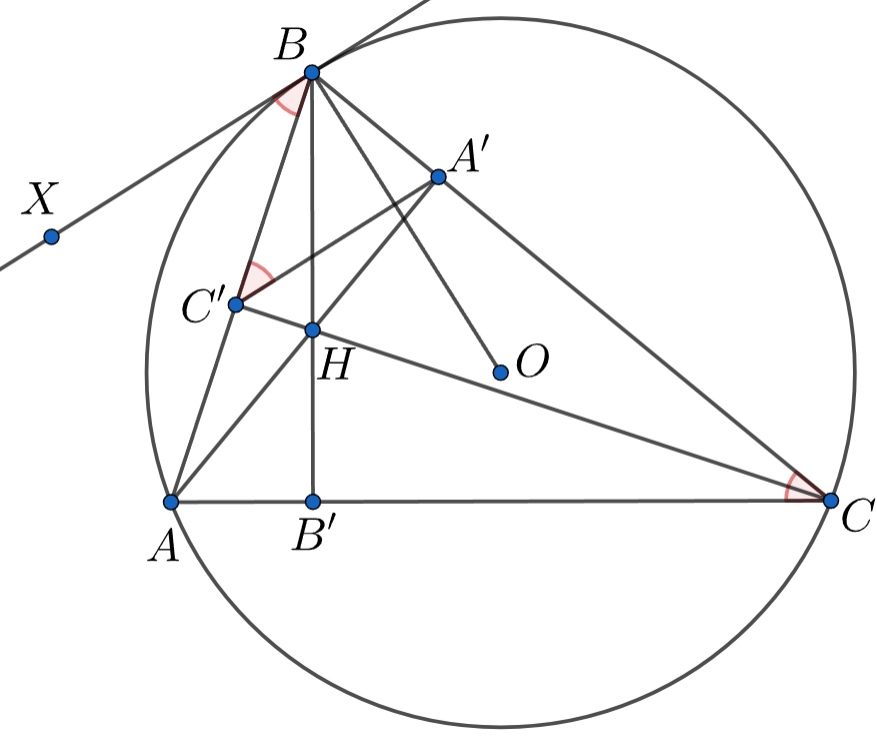
В силу антипараллельности и
имеем
Также
как угол между хордой и касательной. Теперь
видно, что
Понятно, что достаточно доказать перпендикулярность и
Это так, потому что
является радиусом проведенным к точке
касания прямой
с окружностью.
Ошибка.
Попробуйте повторить позже
Высоты и
пересекают описанную окружность остроугольного треугольника
в точках
и
Докажите, что
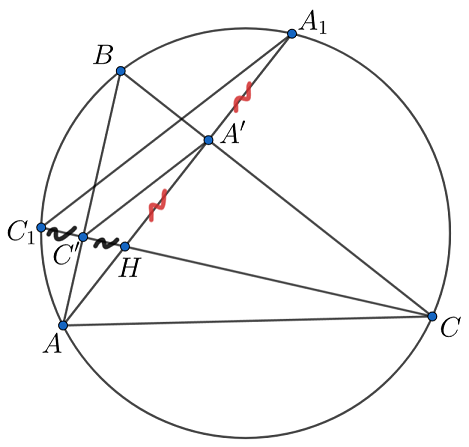
По свойству ортоцентра — середина
— середина
Тогда
— средняя линия в
откуда
Ошибка.
Попробуйте повторить позже
Четырёхугольник, диагонали которого взаимно перпендикулярны, вписан в окружность. Докажите, что продолжение перпендикуляра из точки пересечения диагоналей к одной из сторон делит противоположную сторону пополам.
Назовём этот четырёхугольник точку пересечения диагоналей обозначим через
и пусть прямая
перпендикулярна
и
пересекает сторону
в точке
![]()
Первое решение.
Поскольку , то
. Поскольку
(где
является высотой в прямоугольном
треугольнике
, то
, как вертикальные, откуда
будет медианой в прямоугольном
треугольнике.
Второе решение.
Прямые и
антипараллельны относительно угла
а высота
прямоугольного треугольника
как известно,
является также симедианой в этом треугольнике, соответственно делит антипараллельный отрезку
отрезок
пополам.
Замечание.
Указанный в задаче факт известен как “теорема Брахмагупты”. Но так задача заключается в том, чтобы доказать напрямую это утверждение, не следует просто так ссылаться на эту теорему! Решение “по теореме Брахмагупты задача очевидна” будет оценено в 0 баллов!
по теореме Брахмагупты задача очевидна
Ошибка.
Попробуйте повторить позже
Дан вписанный четырёхугольник диагонали которого не перпендикулярны.
и
— проекции на диагональ
вершин
и
соответственно.
и
— проекции на диагональ
вершин
и
соответственно. Докажите, что
— вписанный
четырёхугольник.
![]()
Первое решение.
Так как — вписанный, то
Заметим, что так как
то
— вписанный, а
это означает, что
Аналогично получим, что
— вписанный, то есть
Тогда
имеем:
Равенство означает вписанность четырёхугольника
Второе решение.
Рассмотрим антипараллельность относительно угла между прямыми и
Условие задачи означает, что
Так как то
Тогда по свойству антипараллельности
Аналогично получим, что откуда
и
так что
— вписанный.
Ошибка.
Попробуйте повторить позже
Окружности пересекаются в точках и
Через
и
проведены прямые
и
соответственно, пересекающие первую
окружность в точках
и
вторую в точках
и
Докажите, что
![]()
Прямая антипараллельна прямым
и
относительно пары прямых
так как
и
— вписанные
четырехугольники.
По свойству антипараллельности и
параллельны, как прямые, антипараллельные прямой
относительно пары прямых
Замечание.
В разных источниках этот факт известен как “лемма Фусса” или “теорема Рейма” . Но в данном случае задача заключается в том, чтобы напрямую доказать эту лемму, поэтому ссылаться на неё без доказательства некорректно.
Ошибка.
Попробуйте повторить позже
Окружности и
пересекаются в точках
и
Прямая, проходящая через
пересекает
в точке
и
в точке
Прямая, проходящая через
пересекает
в точке
и
в точке
Докажите, что
![]()
В силу вписанности четырёхугольника имеем:
(последний переход справедлив, потому что — вписанный). Это даёт требуемое.
Ошибка.
Попробуйте повторить позже
Пусть и
— высоты треугольника
и
— проекции точки
на прямые
и
Аналогично определим
точки
и
и
Докажите, что длины отрезков
и
равны.
![]()
Заметим, что четырехугольник вписанный. Поэтому
Аналогично Также прямые
и
антипараллельны, как и прямые
и
Отсюда следует, что
прямые
и
параллельны и
Отсюда
и
и
Аналогично и для
отрезка.
Ошибка.
Попробуйте повторить позже
Пусть – высота треугольника
Пусть
и
– высоты треугольников
и
соответственно. Докажите,
что точки
и
лежат на одной окружности.
![]()
Поскольку , то
можно вписать в окружность, поэтому
и
равны как
вписанные углы. Но за счёт прямоугольных треугольников
. Из равенства углов
и
следует
вписанность
.
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Пусть – высота треугольника
Пусть
и
— высоты треугольников
и
Докажите, что точки
и
лежат на одной окружности, где
и
— середины сторон
и
![]()
Поскольку то
можно вписать в окружность, поэтому
и
равны как
вписанные углы. Но за счёт прямоугольных треугольников
Тогда
антипараллелен
относительно
Средняя линия
откуда сразу же следует, что
антипараллелелен
относительно того же
что и означает вписанность
Ошибка.
Попробуйте повторить позже
Пусть и
высоты, а
и
- биссектрисы треугольника
. Известно, что
. Верно ли, что
![]()
Мы знаем, что антипараллельно
относительно
, а с учётом
следует, что
– вписанный
четырёхугольник. Тогда
и
равны как вписанные, значит, углы треугольника
при основании
равны.
да
Ошибка.
Попробуйте повторить позже
Дан треугольник Касательная в точке
к его описанной окружности пересекает прямую
в точке
Касательные к
описанной окружности треугольника
в точках
и
пересекаются в точке
Докажите, что прямая
делит отрезок
пополам.
![]()
Из основной задачи о симедиане следует, что прямая содержит симедиану треугольника
По теореме об угле между
касательной и хордой
имеем
откуда
и имеют общий угол
То есть отрезки
и
антипараллельны относительно угла
(предельный случай антипараллельности, когда получаем не
вписанный четырёхугольник, а касательную к описанной около треугольника окружности), а при симметрии относительно
биссектрисы и гомотетии симедиана
треугольника
перейдёт в медиану
треугольника
что и означает
требуемое.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике высоты
,
и
пересекаются в точке
. Из точки
провели перпендикуляры к
прямым
и
, которые пересекли лучи
и
в точках
и
соответственно. Докажите, что перпендикуляр,
опущенный из точки
на прямую
, проходит через середину отрезка
.
Заметим, что высоты к и
симметричны относительно биссектрисы
, поскольку
и
антипараллельны
относительно угла
. Для получения требуемого результата достаточно показать, что
является симедианой
.
![]()
Заметим, что (поскольку
. Тогда
(пользуемся вписанностью
). Аналогично в силу симметрии обозначений
. В итоге
и
. Так как симедиана — это геометрическое место точек, расстояния от которых до сторон относятся так же, как и эти
стороны, то задача решена.
Ошибка.
Попробуйте повторить позже
В окружность вписан четырёхугольник , диагонали которого взаимно перпендикулярны и пересекаются в точке
Прямая,
проходящая через точку
и перпендикулярная к
, пересекает сторону
в точке
Найдите длину медианы треугольника
, проведённую из вершины
если
![]()
Поскольку , то
. Поскольку
(
) является высотой в прямоугольном
треугольнике
, то
, как вертикальные, откуда
будет медианой в прямоугольном
треугольнике.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Можно также заметить, что прямые и
антипараллельны относительно угла
, а высота
прямоугольного треугольника
, как известно, является также симедианой в этом треугольнике, соответственно делит
антипараллельный отрезку
отрезок
пополам. Данный факт известен в олимпиадном сообществе как “теорема Брахмагупты” и
при правильной формулировке может быть использован без доказательства.
_________________________________________________________________________________________________________________________________________________________________________________
Далее, в силу перпендикулярности диагоналей четырёхугольника:
по теореме Пифагора из треугольника
из треугольника
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике провели высоту
медиану
и биссектрису
Точки
и
— ортогональные
проекции вершин
и
на прямую
Докажите, что точки
и
лежат на одной окружности.
Источники:
Рассмотрим без ограничения общности Тогда точка
лежит внутри треугольника
, а точка
вне
его.
Первое решение.
Построим описанную окружность треугольника , тогда продолжение биссектрисы
пересечет ее в точке
,
являющейся серединой дуги
. Тогда
, то есть медиана
равнобедренного треугольника
будет также и
высотой.
![]()
Так как , то получим, что
. Так как
аналогично получаем, что
.
Но углы равны, как вписанные углы, опирающиеся на одну дугу.
В итоге . Но из равенства углов
следует, что точки
лежат на одной
окружности.
Второе решение.
Обозначим через и
точки пересечения прямых
и
и
соответственно.
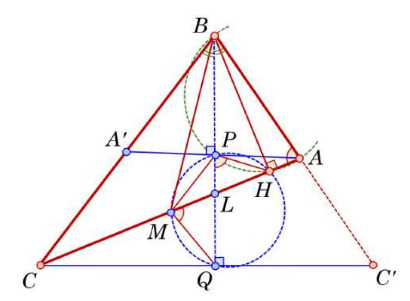
Поскольку — биссектриса и
треугольники
и
— равнобедренные, и значит,
и
В треугольнике точки
и
— середины сторон
и
поэтому
— средняя линия, и значит,
Аналогично,
Следовательно,
Возможны два случая:
a) Точки
и
лежат на одной окружности с диаметром
поэтому четырёхугольник
— вписанный.
Значит,
Следовательно, точки и
лежат на одной окружности.
б) тогда точки
и
лежат на одной окружности с диаметром
поэтому четырёхугольник
—
вписанный. Значит,
Следовательно, точки и
лежат на одной окружности.
Ошибка.
Попробуйте повторить позже
Пусть — высоты треугольника
Прямая
пересекает описанную окружность треугольника
в точках
и
Точки
и
симметричны
и
относительно
и
соответственно. Докажите, что
Источники:
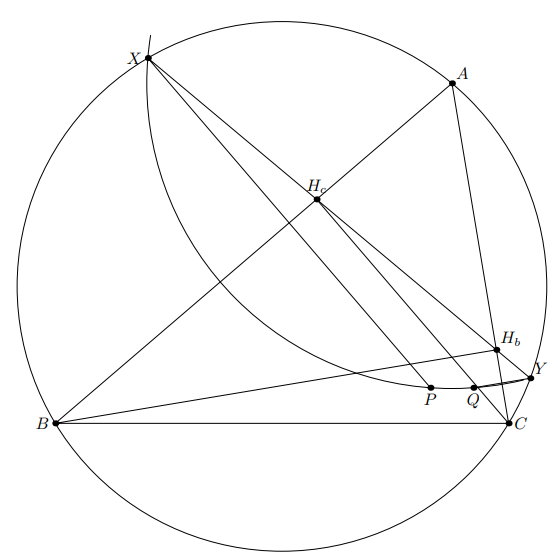
Пусть — центр описанной около треугольника
окружности. Так как прямая
симметрична высоте треугольника из вершины
относительно биссектрисы из той же вершины, а
то
т.е.
— серединный перпендикуляр к отрезку
Следовательно,
и четырехугольник
вписанный. Поэтому прямые
и
антипараллельны
относительно прямых
и
которые параллельны высотам треугольника. Но
и
также антипараллельны относительно
высот, значит,



