Закл (финал) 10 класс
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Найдите все натуральные для которых существует такое чётное натуральное
что число
является точным квадратом.
Источники:
Подсказка 1:
Попробуйте сначала вручную разобраться с n = 1, 2, 3. Для этих случаев достаточно вспомнить утверждение о том, что если произведение двух взаимно простых чисел — квадрат, то каждое из них также является квадратом. В частности, при n = 3 надо поработать с нодами скобок a - 1, a + 1, a² + a + 1. Быть может, этот ход мыслей можно развить и для больших n?
Подсказка 2:
Итак, скорее всего вы поняли, что n = 1, 2 подойдёт, а n = 3 — нет. Чем остальные случаи отличаются. Например, если n > 3, то оно находится между двумя натуральными степенями двойки. То есть существует такое натуральное k, что 2^k ≤ n < 2^{k + 1}. Подумайте, как это можно использовать.
Подсказка 3:
Если записать скобку a^{2^k} – 1 как (a^{2^{k – 1}} – 1)(a^{2^{k – 1}} + 1), то становится ясно, что все произведение состоит из скобки a^{2^{k – 1}} + 1 и скобок вида a^m – 1. А как насчёт того, чтобы посмотреть на нод выражений a^{2^{k – 1}} + 1 и a^{2^k} – 1 с произвольной скобкой a^m – 1?
Подсказка 4:
Нод второго выражения и a^m – 1 кратен ноду первого выражения и a^m - 1. Чтобы было проще работать, вот вам интересный факт: нод второй скобки и a^m – 1 равен a^нод(2^k, m) – 1. Осталось поработать с нодом 2^k и m.
Подсказка 5:
Исходя из выбора k, ясно, что нод 2^k и m не превышает 2^{k – 1}. Попробуйте теперь показать, что ноды выражений a^{2^{k – 1}} + 1 и a^{2^k} – 1 с a^m – 1 совпадают. Кажется, это раскроет идею подсказки 3.
Подсказка 6:
Стало быть, a^{2^{k – 1}} + 1 — точный квадрат. А вас это не смущает?
Заметим, что для подойдёт
Для
подойдёт
Предположим, что для нашлось требуемое число
Тогда число
является точным квадратом. Поскольку
числа и
взаимно просты. Раз число
нечётно, числа
и
также взаимно просты. Следовательно,
числа
и
— точные квадраты. В частности, число
при делении на 3 может давать лишь остаток 0 или 1, а
тогда число
не делится на 3. Отсюда
значит, числа и
также являются точными квадратами. Но второе являться квадратом не может,
поскольку
Противоречие.
Осталось доказать, что требуемого не существует при
Предположим, что такое
нашлось. Возьмём такое натуральное
что
Поскольку
число
представляется в виде произведения и нескольких множителей вида
где
и
Докажем, что множитель взаимно прост со всеми остальными множителями в этом разложении. Пусть
и
имеют некоторый общий делитель
Тогда и НОД
и
кратен
Но
Поскольку и
число
не может делиться на
Таким образом,
— степень двойки,
не превосходящая
Следовательно,
делится на НОД
и
а, значит, делится и на
Поскольку
чётно, числа
и
не имеют общих делителей, отличных от 1, значит,
что и
требовалось.
Множитель взаимно прост со всеми остальными множителями в произведении, являющемся точным квадратом, поэтому он
сам является точным квадратом. Тогда
и
— отличающиеся на 1 квадраты натуральных чисел, что невозможно. Значит,
наше предположение неверно, и для
требуемых чисел
не найдётся.
и
Ошибка.
Попробуйте повторить позже
Дано натуральное число Натуральные числа
выписывают на доске в строчку в некотором порядке. У каждых двух стоящих
рядом чисел вычисляют их НОД (наибольший общий делитель) и записывают этот НОД на листке. Какое наибольшее количество
различных чисел может быть среди всех
выписанных на листке чисел?
Источники:
Подсказка 1:
Давайте начнем с оценки. Вот если есть два различных числа a, b и их НОД равен d, можно ли как-то оценить эти числа, используя d? И как, используя эти оценки, оценить сверху d некоторым выражением от n?
Подсказка 2:
Одна из самых очевидных оценок: min(a, b) ≥ d, max(a, b) ≥ 2d. Отсюда следует, что n ≥ 2d, откуда d ≤ [n / 2]. Осталось привести пример.
Подсказка 3:
Чтобы найти расстановку, для которой любое число d ≤ [n / 2] будет выписано, можно сделать так, чтобы числа вида d и 2d стояли рядом.
Подсказка 4:
Тут на помощь могут прийти числовые цепочки вида a, 2a, 2²a, ... Подумайте, почему они могут быть полезны, и как реализовать расстановку с ними?
Оценка. Предположим, что какое-то из выписанных на листке чисел больше скажем,
Тогда наибольшее из
чисел
не меньше
что больше
– противоречие (НОД двух чисел, не превосходящих
не превосходит
). Значит,
каждый из написанных
ов не превосходит
потому количество различных
ов не может превышать
Пример. Разобьём все числа от до
на цепочки вида
где
— нечётное число, не превосходящее
Выпишем
в строчку цепочки одну за другой. Тогда для любого натурального
найдётся цепочка, в которой встречается
а следующее за
число будет
Видим, что каждое натуральное
будет выписано на листке.
Ошибка.
Попробуйте повторить позже
Петя и Вася играют в игру на изначально пустой клетчатой таблице делая ходы по очереди. Начинает Петя. За свой
ход игрок вписывает в некоторую пустую клетку любую заглавную букву русского алфавита (в каждую клетку можно
вписать ровно одну букву). Когда все клетки будут заполнены, Петя объявляется победителем, если найдутся четыре подряд
идущие клетки по горизонтали, в которых слева направо написано слово «ПЕТЯ», или найдутся четыре подряд идущие
клетки по вертикали, в которых сверху вниз написано слово «ПЕТЯ». Сможет ли Петя выиграть независимо от действий
Васи?
Источники:
Подсказка 1:
Попробуйте придумать выигрышную стратегию для Васи.
Подсказка 2:
Хорошей идеей будет выбрать некоторую букву, которой нет в слове ПЕТЯ, и некоторым образом с её помощью блокировать появление данного слова. Как это сделать?
Подсказка 3:
Попробуйте придумать такой алгоритм выставления буквы, при котором будет блокироваться появление сочетания букв ПЕ по горизонтали и ТЯ по вертикали. Как нужно отвечать на ходы Пети, чтобы добиться этого?
Опишем выигрышную стратегию Васи. Пусть Вася все время пишет букву «Ю» в клетку согласно следующим ниже условиям; а если указанная клетка не существует или уже занята, а также если Петя ставит любую букву отличную от «П», «Е», «Т», «Я», то пусть Вася ставит «Ю» в любую свободную клетку.
Если Петя в некоторой клетке пишет букву «П», то Вася пишет «Ю» в клетке, соседней с ней справа; если Петя пишет букву «Е», то Вася пишет «Ю» в клетке, соседней с ней слева; если Петя пишет букву «Т», то Вася пишет «Ю» в клетке, соседней с ней снизу; если Петя пишет букву «Я», то Вася пишет «Ю» в клетке, соседней с ней сверху.
Из первых двух условий следует, что в двух соседних по горизонтали клетках не могло появиться «ПЕ», читаемое слева направо. В самом деле, предположим, что горизонтальное «ПЕ» появилось; тогда после появления первой из этих двух букв Вася, согласно описанной стратегии, сразу займёт место второй из этих букв — противоречие. Аналогично, в двух соседних по вертикали клетках не могло появиться «ТЯ», читаемое сверху вниз.
не сможет
Ошибка.
Попробуйте повторить позже
Внутри треугольника отмечена точка
На отрезке
отмечена точка
а на отрезке
— точка
так, что
описанные окружности треугольников
и
касаются прямой
Через точки
и
провели прямые,
проходящие через центр описанной окружности треугольника
а через точки
и
— прямые, проходящие через центр
описанной окружности треугольника
Докажите, что существует окружность, которая касается четырёх проведённых
прямых.
Источники:
Подсказка 1:
Наличие касания двух окружностей с AP должно вызвать у вас желание написать степень точки A относительно этих окружностей.
Подсказка 2:
Скорее всего вы получили равенство AB • AQ = AC • AR, которое говорит о том, что BCQR — вписанный. Попробуйте найти на рисунке какую-нибудь точку, для которой проще всего доказать, что она равноудалена от нужных четырех прямых.
Подсказка 3:
Проще всего это сделать для точки O — центра окружности, описанной около BCRQ. Что для этого нужно доказать?
Подсказка 4:
Пусть O₁, O₂ — центры окружностей (BPC) и (QPR). Для этого достаточно равенства направленных углов O₁BO и OQO₂. Кстати, почему?
Подсказка 5:
Попробуйте выразить угол OQO₂ через углы RPQ и RCQ. Для этого давайте вспомним, что в треугольнике величина центрального угла его описанной окружности, опирающийся на сторону a, некоторым образом связана с величиной угла, противолежащего а. В дальнейшем доказательстве вам поможет теорема об угле между хордой и касательной.
Поскольку
четырёхугольник — вписанный. Пусть
— центр окружности
Обозначим через
и
центры окружностей
и
Покажем, что прямые
равноудалены от
Так как
для этого достаточно установить равенство направленных углов
Здесь первое и последнее равенства очевидны из симметрии относительно серединных перпендикуляров к и
Остаётся доказать равенство Из счёта углов получаем
Аналогично
Значит, эквивалентно равенству
или
Из касания окружностей и
следует
что из суммы углов четырёхугольника равно
Тем самым, преобразуется к виду
что верно.
![]()
Ошибка.
Попробуйте повторить позже
На плоскости отмечены точек, никакие три из которых не лежат на одной прямой, и проведены все отрезки между ними. Гриша
поставил на каждом проведённом отрезке вещественное число, по модулю не превосходящее 1, и для каждой шестёрки отмеченных
точек посчитал сумму чисел на всех 15 отрезках, соединяющих их. Оказалось, что каждая такая сумма по модулю не
меньше числа
при этом среди таких сумм есть как положительная, так и отрицательная. При каком наибольшем
это
возможно?
Источники:
Подсказка 1
Рассмотрим граф с вершинами в отмеченных точках. Имеются шестёрки с суммами разных знаков. Поскольку мы работаем с кликами, подумайте: какой вид рассуждений о непрерывности может помочь при переходе между шестёрками вершин? Что происходит при замене одной вершины в шестёрке?
Подсказка 2
Если найдутся две шестёрки с разными знаками сумм, отличающиеся одной вершиной, то их объединение содержит 7 вершин. Чем интересно данное множество из 7 вершин? Сколько подшестёрок оно содержит и можно ли сказать что-то про знаки сумм этих шестёрок?
Подсказка 3
Возможно, для анализа данной клики на 7 вершинах стоит её упростить, например, сделав числа на рёбрах одинаковыми.
Подсказка 4
Классифицируйте вершины в этом 7-вершинном множестве: назовите вершину "типа A", если при её удалении сумма в оставшейся шестёрке отрицательна, и "типа B" — если положительна. Пусть k — количество вершин типа A. Какие значения k существенны, а какие аналогичны между собой?
Подсказка 5
Разделите рёбра на три типа: AA (между вершинами типа A), AB (между A и B), BB (между вершинами типа B). Если заменить веса на рёбрах каждого типа на их среднее арифметическое, то как это преобразование повлияет на суммы в подшестёрках? Сохранятся ли условия задачи?
Подсказка 6
Анализировать такую 7-ку вершин намного легче. Можно записать неравенства на искомую константу С при помощи новых значений на ребрах.
Подсказка 7
Какие бы ограничения на константу ни были найдены ранее, всё равно нужно предоставить числа для рёбер, которые будут её реализовывать. Может быть, вид 7-ки после замены чисел на средние можно распространить на весь граф?
Рассмотрим граф, вершинами которого являются отмеченные точки, а рёбрами — проведённые отрезки.
Оценка. Докажем оценку Условие гласит, что в нашем полном графе есть как шестёрки вершин, сумма на рёбрах между
которыми положительна, так и шестёрки, сумма на рёбрах между которыми отрицательна. Тогда найдутся две шестёрки,
отличающиеся заменой только одной вершины, такие, что у одной из них сумма положительна, у другой отрицательна. В
самом деле, возьмём шестёрку с положительной суммой, и будем превращать её в шестёрку с отрицательной суммой, меняя
вершины по одной, — на каком-то шаге произошло изменение знака, шестёрки, которые были до и после этого шага – искомая
пара.
Далее работаем с полным подграфом на множестве из семи вершин – объединении вышеописанной пары шестёрок. Рассмотрим все
семь шестёрок, которые можно получить выбрасыванием одной вершины из
Пусть среди них
с отрицательными суммами —
получающиеся выбрасыванием вершин
будем называть эти вершины
-вершинами, а соответствующие шестёрки –
-шестёрками), и
с положительными суммами — получающиеся выбрасыванием вершин
(будем называть эти
вершины
-вершинами, а соответствующие шестёрки –
-шестёрками). Рёбра между двумя
-вершинами будем называть
-рёбрами, между двумя
-вершинами —
-рёбрами, а рёбра, соединяющие
-вершину с
-вершиной —
-рёбрами.
Из изначальной расстановки чисел на рёбрах, соединяющих вершины множества получим новую расстановку, заменив все числа на
-рёбрах на число
равное их среднему арифметическому, и аналогично заменив все числа на
-рёбрах на их среднее
арифметическое
а все числа на
-рёбрах на их среднее арифметическое
Очевидно,
так как все старые
числа по модулю не превосходят 1.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Подграф с новыми числами на рёбрах удовлетворяет условию с той же константой
Доказательство леммы. Заметим, что для каждого -рёбра есть одно и то же количество
-шестёрок, в которые входят оба его
конца. И наоборот, для любой
-шестёрки среди 15 рёбер между её вершинами есть одно и то же количество
-рёбер. То же верно для
-рёбер и для
-рёбер. Значит, сумма
чисел на рёбрах в
-шестёрке в новой расстановке есть среднее сумм по всем
-шестёркам в старой расстановке, то есть среднее нескольких чисел, не больших –
значит,
Аналогичное утверждение
верно для сумм в
-шестёрках. Лемма доказана.
_________________________________________________________________________________________________________________________________________________________________________________
Далее изучаем новую расстановку. Рассмотрим случаи.
Случай Иными словами, есть ровно одна
-шестёрка, на которой пятнадцать
-рёбер, и шесть
-шестёрок, на каждой
из которых десять
-рёбер и пять
-рёбер. Имеем систему неравенств:
Умножим первое на сложим со вторым, умноженным на 3, получим
откуда
Случай Теперь у нас две
-вершины и пять
-вершин, то есть на
-шестёрке есть десять
-рёбер и пять
-рёбер,
а на
-шестёрке – шесть
-рёбер, восемь
-рёбер и одно
-ребро. Имеем
Исключая получаем
значит,
Случай Аналогично предыдущему, имеем
Избавляясь на этот раз от получаем
откуда
Случаи сводятся к рассмотренным умножением всех чисел на
что ведёт к замене
Итак, оценка
доказана.
Пример. Любое число вершин от двух до 999995 объявим вершинами типа остальные – вершинами типа
На всех рёбрах между
двумя вершинами типа
напишем число
на всех остальных – число 1. Тогда, если в шестёрке вершин хотя бы пять
-вершин, то
сумма в ней не больше
а иначе – не меньше
Ошибка.
Попробуйте повторить позже
На периметре треугольника выбраны точки
так, что при обходе периметра точки встречаются в
порядке
Оказалось, что
Докажите, что периметры треугольников, образованных тройками прямых
и
равны.
Источники:
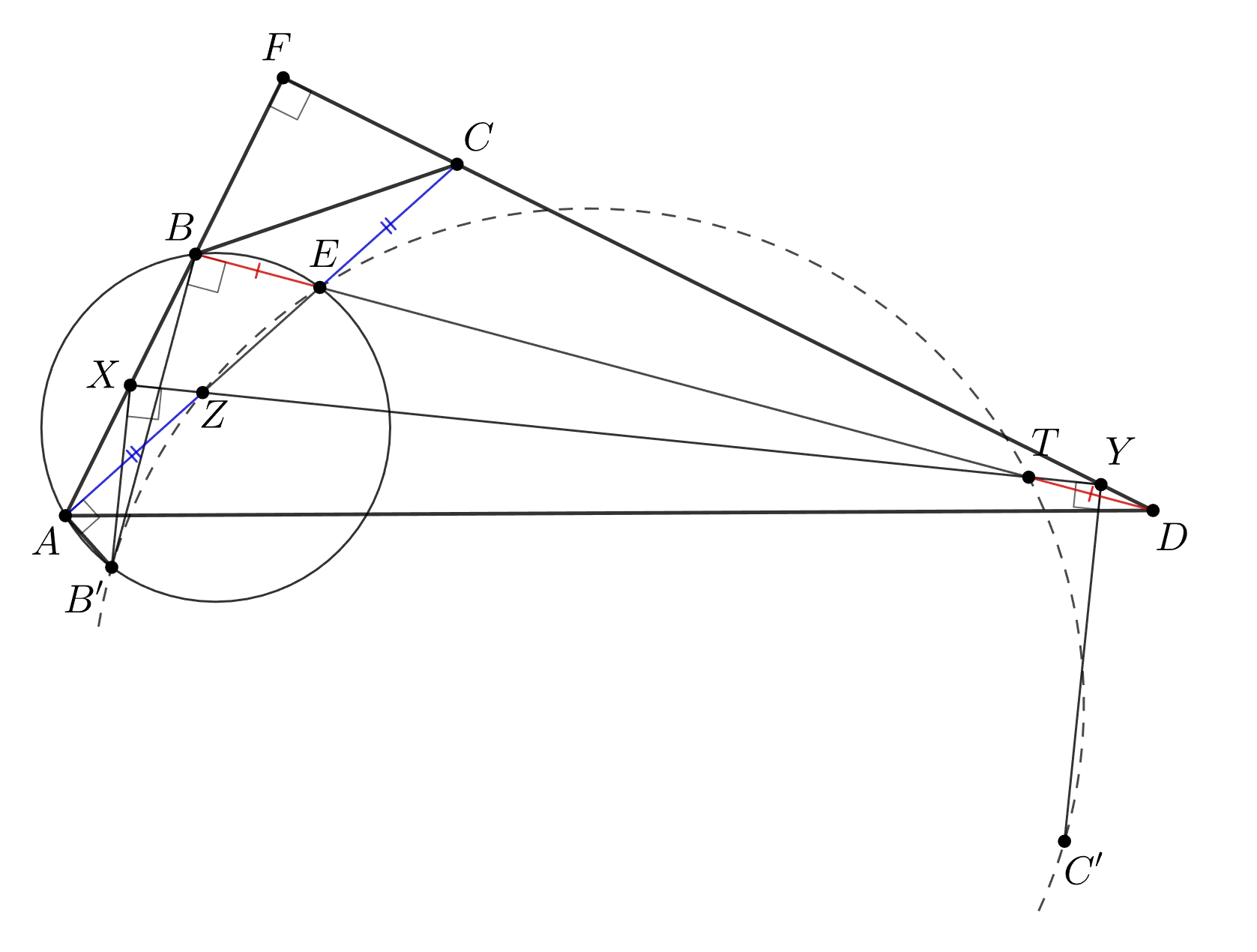
Начнём со следующей полезной леммы.
Лемма. Пусть точки и
выбраны соответственно на сторонах
и
параллелограмма
так, что
Тогда точка
равноудалена от прямых
и
Доказательство. Поскольку и
имеем
Так как
отсюда и следует, что
расстояния от точки
до прямых
и
равны.
.png)
_________________________________________________________________________________________________________________________________________________________________________________
Перейдём к решению. Пусть прямые из условия образуют треугольники и
(точки обозначены как на рис.). Выберем
точку
так, что
— параллелограмм; согласно лемме, точка
равноудалена от прямых
и
; значит,
существует окружность с центром
касающаяся этих прямых в некоторых точках
и
соответственно. Тогда из равенств
отрезков касательных вытекает, что
Аналогично получаем, что и
Складывая полученные три равенства, получаем
требуемое равенство периметров.
Ошибка.
Попробуйте повторить позже
При каком наименьшем для любого многочлена
степени 100 с вещественными коэффициентами найдётся такой многочлен
степени не выше
с вещественными коэффициентами, что графики
и
имеют ровно 100 общих
точек?
Источники:
Положим
Покажем, как подобрать нужный многочлен степени не выше
для данного многочлена
степени
При домножении
на
ненулевую константу условие не поменяется (многочлен
можно домножить на ту же константу), поэтому считаем, что старший
коэффициент
равен
так что
Возьмём произвольный набор различных чисел
дающих в сумме
и положим
так что Видим, что у
и
совпадают коэффициенты при
и при
поэтому степень
не превышает
С другой стороны, абсциссы точек пересечения графиков
и
— это в точности корни многочлена
а их ровно
Покажем, что не работает. Пусть дан многочлен
а
— многочлен степени не выше
Предположим, что
графики
и
пересекаются в
точках, имеющих абсциссы
Но тогда многочлен
степени
имеет
вещественных корней
С другой стороны, у
коэффициенты при
и
равны 0. Но тогда по теореме
Виета
Отсюда
следовательно,
что противоречит тому, что различны.
98
Ошибка.
Попробуйте повторить позже
В программу соревнования входит 25 видов спорта, в каждом из которых определяется один победитель, получающий золотую медаль. В
соревновании участвуют 25 спортсменов, каждый — во всех 25 видах спорта. Имеется 25 экспертов, каждый из которых должен сделать
прогноз, сколько золотых медалей получит каждый спортсмен, при этом в его прогнозе количества медалей должны являться целыми
неотрицательными числами с суммой 25. Эксперта признают компетентным, если он верно угадает количество золотых медалей хотя бы у
одного спортсмена. При каком наибольшем эксперты могут сделать такие прогнозы, что хотя бы
из них будут признаны
компетентными независимо от исхода соревнования?
Источники:
Подсказка 1:
Казалось бы, задача на оценку + пример. Обычно в этом случае мы сначала делаем оценку, потом под неё подгоняем пример. Здесь же стоит делать наоборот, объясним мотивацию. Пусть мы хотим доказать, что 20 нельзя (например). Доказывать это прямо абсолютно непонятно как, значит, можно попробовать от обратного. Но условие на то, что 20 можно, нам не даёт ровным счётом ничего, мы просто знаем этот факт, и про оценки каждого эксперта мы ничего сказать не можем. В таких случаях оценка чаще всего тривиальна (что-то около границ), а основную сложность составляет пример. Подумайте, какие наборы оценок у экспертов нам лучше использовать для примера?
Подсказка 2:
Поисследуем наборы. Имеем 25 человек и 25 медалей, которые распределены между ними. По принципу Дирихле, всегда найдётся человек, у которого не более одной медали. Что мы тогда можем сказать про спортсменов, у которых вовсе нет медалей (будем называть таких нулевыми)?
Подсказка 3:
Либо среди спортсменов есть хотя бы один нулевой, либо у всех ровно по одной медали. Отлично, то есть нулевых нет только в единственном случае. Значит, можно попробовать организовать высокую вероятность компетенции, основываясь на нулевых. Какой набор (маску) для этого нужно применить?
Подсказка 4:
Разумеется, ту, в которой много нулей, чтобы наверняка хотя бы в один попасть. Однако нельзя забыть про случай, когда у каждого по одной медали. Для этого тоже нужно применить особенную маску, которая будет идентифицировать этот случай. Какую же?
Подсказка 5:
Да, 25 единиц (такую маску назовём единичной). Итого, у одного эксперта единичная маска (назовём его единичным), осталось придумать ещё 24. Причём понятно, что в случае компетентности единичного эксперта мы хотим, чтобы бóльшая часть остальных тоже была компетентна. То есть в остальных масках должно присутствовать много нулей и хотя бы 1 единица. Какая самая тривиальная маска удовлетворяет этим условиям?
Подсказка 6:
Маска вида: 1 единица, 23 нуля и все остальные. Какой набор тогда мы получаем для остальных 24 спортсменов?
Подсказка 7:
Например: (1, 0, ..., 0, 24), (0, 1, 0, ..., 0, 24), ..., (0, ..., 0, 1, 24). Очевидно, если единичный компетентен, то у нас 25 компетентных экспертов. Что же происходит, когда он некомпетентен?
Подсказка 8:
Докажите, что в этом случае хотя бы 3 спортсмена являются нулевыми. Отсюда немедленно следует, что все остальные эксперты компетентны. Итого, имеем пример на 24. Осталось сделать оценку.
Подсказка 9:
Нам нужно доказать, что нет такого набора масок для экспертов, что все всегда компетентны. Это равносильно тому, что всегда можно подобрать такой исход соревнований, что хотя бы один эксперт будет некомпетентным. Придётся разобрать несколько случаев.
Подсказка 10:
Когда у эксперта в маске есть нули и когда их нет. Оба случая достаточно просты. Уверены, вы справитесь. Успехов!
Оценка. Покажем, что то есть, что любой эксперт может оказаться некомпетентным. Если этот эксперт считает, что все
спортсмены возьмут по одной медали, опровергнем его результатом
Иначе эксперт считает, что несколько (хотя бы один)
спортсменов получат 0 медалей. Тогда распределим все медали между этими спортсменами так, чтобы каждый из них получил хотя бы одну
медаль. В таком случае эксперт не угадает ни одного количества медалей.
Пример. Пусть прогноз одного эксперта — а прогнозы остальных — (1, 0, …, 0, 24), (0, 1, …, 0, 24), …, (0, 0, …, 1, 24) (на
последнем месте 24, и ещё одна единица).
Если некомпетентным оказался первый эксперт, то в исходе точно есть хотя бы три нуля, иначе хотя бы в 23 позициях количество
медалей не меньше 2, и тогда общее количество медалей не меньше — противоречие. Но тогда каждый из остальных экспертов
компетентный.
Предположим теперь, что двое экспертов, отличных от первого, оказались некомпетентными. Тогда в двух позициях их прогнозы — 0 и 1
медалей, а значит, в реальном исходе в этих позициях не менее 2 медалей. Кроме того, ещё в 22 позициях прогнозы обоих экспертов — нули,
значит, в реальном исходе в этих позициях не менее 1 медали. Тогда общее количество медалей не меньше —
противоречие.
24
Ошибка.
Попробуйте повторить позже
Пусть и
— различные простые числа. Дана бесконечная убывающая арифметическая прогрессия, в которой встречается каждое из
чисел
и
Докажите, что в этой прогрессии обязательно встретятся числа
и
Источники:
Подсказка 1:
Начнем с того, что в прогрессии могут быть и нецелые числа. Подумайте, можно ли от них как-то избавиться?
Подсказка 2:
Если и есть нецелые числа, то они рациональные. Попробуйте обосновать, что если вычеркнуть из прогрессии все нецелые числа, то оставшиеся тоже образуют арифметическую прогрессию.
Подсказка 3:
Сформулируем несколько утверждений, которые помогут решить задачу. Во-первых, если в целочисленной арифметической прогрессии есть два числа a и b, то a − b кратно d. Во-вторых, если в прогрессии с разностью d есть a, то b ей будет принадлежать тогда и только тогда, когда a − b кратно d.
Подсказка 4:
Значит, d является делителем p²⁴ − p²³. Нужно, чтобы оно также делило p²³ − p. Чтобы было проще, подумайте, может ли d делиться на p?
Вычеркнем все нецелые числа из прогрессии (если они есть). Ясно, что после вычёркивания остаётся бесконечная убывающая
арифметическая прогрессия, состоящая из целых чисел. Пусть её разность равна —
Заметим, что делится на
значит,
не делится на
иначе
должно будет делиться на
что неверно. С другой
стороны,
должно являться делителем числа
Поскольку и
взаимно просты,
делится на
Далее,
делится на
поскольку оно равно
Поэтому делится на
и, поскольку
получаем, что
лежит в нашей прогрессии. Аналогично,
лежит в этой
прогрессии.
Ошибка.
Попробуйте повторить позже
Дано нечётное число В клетчатом квадрате
закрашивают
клеток. Какое наибольшее количество трёхклеточных
уголков можно гарантированно вырезать из незакрашенной клетчатой фигуры?
Источники:
Подсказка 1
Представьте, что мы хотим гарантированно найти много уголков. Как можно разбить большой квадрат 2n×2n на более мелкие области, чтобы каждый возможный уголок целиком лежал в одной такой области?
Подсказка 2
Предположим, мы разбили квадрат на n² квадратиков 2×2. Сколько клеток в одном таком квадратике? Сколько из них нужно оставить незакрашенными, чтобы гарантированно можно было вырезать один уголок? Похоже на принцип Дирихле.
Подсказка 3
Допустим, для нечётного размера m мы уже знаем, как построить пример с 2(m−1)² закрашенными клетками, позволяющий вырезать 2m−1 уголков. Можно "вставить" этот меньший квадрат внутрь 2(m+2)×2(m+2) и получить пример для m+2? Какая часть большого квадрата останется "непокрытой" этим меньшим квадратом?
Подсказка 4
В этой рамке ширины 2 нам нужно закрасить дополнительные клетки. Сколько всего клеток нам нужно закрасить в большом квадрате? Сколько уже "запланировано" закрасить во внутреннем квадрате? Сколько клеток нужно закрасить в рамке? Как можно закрасить эти клетки в рамке так, чтобы они "мешали" вырезать уголки только минимальное необходимое количество?
Подсказка 5
Для покраски рамки остаётся 2((m+1)² − (m−1)²) = 8m, такой же длины периметр квадрата 2m×2m. Что, если закрасить клетки, граничащие с "вставленным" квадратом?
Оценка. Разобьём квадрат на
квадратиков
Среди этих квадратиков не более
квадратиков, в которых покрашено хотя бы 2 клетки.
Остальных квадратиков — не менее
Из каждого из них можно вырезать трёхклеточный уголок.
Пример. Построим пример индукцией по нечётным При
закрашенных клеток нет, и можно вырезать один
уголок.
Для перехода выделим в квадрате внешнюю «рамку» шириной в две клетки. В этой рамке закрасим все клетки, примыкающие
к внутренней границе рамки (см. рис.), а в квадрате внутри рамки закрасим клетки по предположению индукции. Общее количество
закрашенных клеток равно
.png)
Осталось понять, сколько уголков можно вырезать в этом примере. Любой уголок из непокрашенных клеток целиком лежит либо в рамке, либо во внутреннем квадрате, таких по предположению
Из рамки же нельзя вырезать более уголков — каждый такой уголок должен содержать хотя бы
клетки одного из угловых
квадратов
а двух уголков, пересекающихся с одним квадратом, вырезать нельзя. Значит, общее количество уголков не
больше
Ошибка.
Попробуйте повторить позже
Дано натуральное число Илья задумал пару различных многочленов степени
(с вещественными коэффициентами), аналогично Саша
задумал пару различных многочленов степени
Лёня знает
его цель — выяснить, одинаковые ли пары многочленов у Ильи и Саши.
Лёня выбирает набор из
вещественных чисел
и сообщает эти числа. В ответ Илья заполняет таблицу
для
каждого
он вписывает в две клетки
-го столбца пару чисел
(в любом из двух возможных порядков), где
и
— задуманные им многочлены. Аналогичную таблицу заполняет Саша. При каком наименьшем
Лёня сможет (глядя на таблицы)
наверняка добиться цели?
Источники:
Подсказка 1
Предположим, Лёня выбрал k = 2n точек. Можем ли мы придумать две разные пары многочленов степени n (P₁, Q₁ и P₂, Q₂), при которых таблицы Ильи и Саши будут одинаковыми, хотя пары многочленов разные. Как можно использовать факт, что в таблице порядок значений P(xᵢ) и Q(xᵢ) не фиксирован?
Подсказка 2
Попробуем "разделить" точки на два набора по n штук. Пусть A(x) обращается в ноль на первом наборе точек, а B(x) — на втором. Какие значения будут принимать многочлены вида ±A ± B в выбранных точках?
Подсказка 3
Теперь пусть Лёня выбрал k = 2n + 1 точек. Предположим, что таблицы Ильи и Саши совпали. Сколько раз каждый многочлен Ильи (P₁ или Q₁) обязан совпасть по значению с каким-то многочленом Саши (P₂ или Q₂) в одной и той же точке xᵢ?
Подсказка 4
Найдется пара многочленов, один Сашин, второй Ильи, у которых значения совпадают хотя бы n + 1 точке. Если два многочлена степени не выше n принимают одинаковые значения в более чем n различных точках, что можно сказать об этих многочленах?
Покажем, что при (а тем более при
) Лёня не сможет однозначно определить определить пару
Пусть он
назвал
Положим
так что для
и
для
Тогда если Илья загадал
и
то в
-м столбце таблицы будут числа
при
и числа
при
Но та же таблица годится для пары
и
её мог загадать Саша.
С другой стороны, покажем, что при таблице Ильи может удовлетворять не более одной пары многочленов
Предположим противное, и есть две такие пары:
и
Тогда
совпадает с
или
хотя бы при
различных
значениях аргумента, пусть, скажем, с
Но тогда
и
— одинаковые многочлены (поскольку их разность — многочлен степени
не выше
имеющий не менее
различных корней). Из таблицы тогда получаем, что значения
и
совпадают в
точке, а тогда и
Ошибка.
Попробуйте повторить позже
Дан выпуклый четырёхугольник в котором
Его диагонали пересекаются в точке
Прямая
пересекает
отрезки
и
в точках
и
соответственно. Известно, что
и
Докажите, что длина
отрезка
не больше диаметра окружности, описанной около треугольника
Источники:
Обозначим через окружность
и через
— её диаметр. Поскольку
то
Из условия следует, что лучи
и
пересекаются в некоторой точке
под прямым углом. Проведем
диаметр
в окружности
Поскольку
точки идут на окружности в порядке
Тогда
Следовательно, треугольники и
подобны по двум углам, поэтому
Полученное равенство означает, что прямоугольные треугольники и
подобны по отношению катетов. Тогда
поэтому точка
лежит на окружности
Заметим, что
— прямая Симcона точки
для
треугольника
поскольку
Тогда и проекция
на прямую
тоже лежит на
то есть
Рассуждая аналогично, мы получаем, что точка диаметрально противоположная
на окружности
лежит на окружности
а также
Таким образом,
— хорда окружности
а
и
— проекции точек
и
на прямую
поэтому
что и требовалось.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание 1. Приведём схему другого решения.
Нетрудно показать, что (например, используя Теорему Менелая). Пусть
— середины
(и
),
(и
),
(и
) соответственно. Пусть
Из прямоугольного треугольника
имеем
Далее,
—
серединный треугольник для треугольника
Легкий счет углов (с использованием медианы прямоугольного треугольника)
дает
Значит, точки лежат на одной окружности, тогда
— хорда окружности (
). Отсюда
что завершает решение.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание 2. На самом деле — диаметр окружности (
), что нетрудно установить счётом углов, но для решения
этого не требуется. Равенство
достигается в том и только в том случае, когда исходный четырёхугольник —
вписанный.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание 3. Приведём план ещё одного подхода к задаче. Используем обозначения из приведённого выше решения, а также введём
новые:
Из теорем Менелая для
и прямой
и прямой
находим:
По теореме синусов для треугольника в силу сказанного выше
Таким образом, достаточно доказать, что Из теорем Менелая для
и прямой
и прямой
легко видеть, что
отсюда
Обозначим
тогда Значит,
последнее равенство получается из прямоугольных треугольников и
Остаётся заметить, что
по неравенству Коши-Буняковского-Шварца, получаем в точности требуемое неравенство ().
Ошибка.
Попробуйте повторить позже
Дана прямолинейная дорога, выложенная из зелёных и красных дощечек (дорога — отрезок, разбитый на отрезки-дощечки). Цвета дощечек чередуются; первая и последняя дощечки — зелёные. Известно, что длины всех дощечек больше сантиметра и меньше метра, а также что длина каждой следующей дощечки больше предыдущей. Кузнечик хочет пропрыгать вперёд по дороге по этим дощечкам, наступив на каждую зелёную дощечку (или границу между соседними дощечками). Докажите, что кузнечик может сделать это так, чтобы среди длин его прыжков встретилось не более 8 различных значений.
Источники:
Подсказка 1
Заметим, что кузнечику нужно точно попадать на зелёные дощечки. Для этого полезно иметь прыжок очень маленькой длины. Представьте, что кузнечик двигается по зелёной дощечке небольшими шагами. Какой минимальный размер прыжка может понадобиться, чтобы достичь границы с красной дощечкой?
Подсказка 2
Чтобы перепрыгнуть красную дощечку длины L (где 1 < L < 100 см), потребуется прыжок длиннее L. Учитывая, что длины дощечек строго возрастают, подумайте: если мы перепрыгнули красную дощечку прыжком длины D, то для следующей (ещё более длинной) красной дощечки потребуется прыжок примерно вдвое больше. Как можно организовать набор прыжков, чтобы покрыть весь диапазон от 1 до >100 см, используя мало различных длин?
Подсказка 3
Рассмотрим прогрессию длин прыжков: l, 2l, 4l, 8l, 16l, 32l, 64l. Будет ли такая последовательность эффективна? Какие ограничения надо наложить на l?
Подсказка 4
Как выбрать l и ε? Самый большой прыжок (64l) должен быть > 100 см (чтобы перепрыгнуть самую длинную красную дощечку), но не сильно. Возьмём l < 2 см (чтобы ε = l/N было достаточно мало при большом N), ε < 0.01 см. Существует ли такое l?
Считаем, что дощечки выложены на числовой прямой. Примем
Возьмем такое, что разность длин любой пары соседних дощечек больше
Отметим на прямой бесконечную в обе
стороны арифметическую прогрессию с разностью
так, чтобы концы дощечек не были отмечены. Кузнечик будет прыгать только по
отмеченным точкам, и длины его прыжков будут из множества
где а натуральное
подберём так, что
и
Стратегия кузнечика будет такой: прыгать вправо по зелёной дощечке на пока возможно, и далее перепрыгивать
очередную красную дощечку прыжком минимальной возможной длины (такая длина найдётся, поскольку длина самого
длинного прыжка больше
). Итак, пусть сделан прыжок длины
из зелёного отрезка через очередной красный
отрезок
Нам остаётся убедиться, что после этого прыжка кузнечик окажется в следующем зелёном отрезке
Предположим, что это не так, и кузнечик из точки
где
перепрыгнул в точку
Видим,
что
значит, в множестве длин прыжков кузнечика есть длина Далее, по выбору
имеем
поэтому можем оценить
Видим, что а значит, кузнечик мог из точки
перепрыгнуть красный отрезок
прыжком более коротким,
чем
Противоречие.
Ошибка.
Попробуйте повторить позже
Дан параллелограмм Точка
— середина дуги
окружности, описанной около треугольника
На отрезке
отмечена точка
а на отрезке
— точка
Известно, что
Докажите, что точки
и
лежат на одной
окружности.
Источники:
Первое решение. Пусть Из равнобедренных треугольников
и
(или из того, что
— центр окружности
) имеем
Для решения задачи остаётся понять, что тому же равен
При гомотетии с центром и коэффициентом
точки
перейдут соответственно в
— середины отрезков
и
. Вместо
найдём
заметив, что
и
— проекции
на
и
а
— центр
параллелограмма, или середина
тем самым,
— проекция
на
Видим, что
лежат на одной окружности с
диаметром
Отсюда
Аналогично Из четырёхугольника
видим, что
что и требовалось.
 (Edited).png)
Второе решение. Достаточно доказать равенство углов (т.е. изогональность
и
относительно
Действительно, тогда
будет лежать на внешней биссектрисе угла
и на серединном перпендикуляре к
а значит, будет
совпадать с серединой дуги
Равенство углов в свою очередь, эквивалентно подобно
Докажем это подобие.
Отметим на луче за точкой
точку
так, что
а на луче
за точкой
точку
так, что
Легко
понять, что треугольники
и
равны по двум сторонам и углу между ними. Тогда
Рассмотрим серединный
перпендикуляр к
тогда он является перпендикуляром к параллельной прямой
а поскольку
то он же является
серединным перпендикуляром к
Таким образом, трапеция
равнобедренная, а раз
— параллелограмм, то
—
также равнобедренная трапеция, причём
и
Аналогичное получим для трапеции
Видим,
что
откуда следует нужное нам
.png)
Ошибка.
Попробуйте повторить позже
Пусть даны натуральные числа и
На прямой даны
белых отрезков и
чёрных отрезков, при этом
и
Известно, что никакие два отрезка одного цвета не пересекаются (даже не имеют общих концов). Также известно, что при любом выборе
белых отрезков и
чёрных отрезков обязательно какая-то пара выбранных отрезков будет пересекаться. Докажите,
что
Источники:
Первое решение. Пронумеруем белые отрезки слева направо как
…,
а чёрные — как
…,
Для
каждого чёрного отрезка
назовём его силой
количество индексов
таких, что
пересекается
как с
так и с
Если с какой-то парой
пересекаются два чёрных отрезка, то они имеют общую
точку, что невозможно по условию. Поэтому каждая такая пара учтена в силе не более, чем одного чёрного отрезка, а
значит,
Рассмотрим следующие групп, состоящих из
белых отрезков каждая: при
группа
состоит из отрезков
…,
а при
группа состоит из отрезков
…,
а также из
…,
(иначе говоря, каждая группа состоит из
последовательных отрезков в циклическом порядке). Для группы
обозначим через
количество чёрных отрезков, не
пересекающихся ни с одним из отрезков в
По условию,
поэтому
С другой стороны, каждый чёрный отрезок пересекается максимум
белыми отрезками, и все эти белые отрезки
расположены подряд. Тогда количество групп, содержащих хотя бы один из этих белых отрезков, не превосходит
Поэтому отрезок учтён хотя бы в
числах вида
Поэтому
Из полученных двух оценок на сумму вытекает, что
что и требовалось доказать.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Предположим, что утверждение задачи для некоторых
неверно:
и при этом условии сумма — минимальная возможная.
Без ограничения общности тогда Возьмём
-й слева белый отрезок
и
-й слева чёрный отрезок
У
какого-то из них правый конец левее.
1) Пусть правый конец левее (или концы совпадают). Тогда правые
чёрных отрезков не пересекаются с левыми
белыми.
Противоречие.
2) Пусть правый конец левее. Выкинем все белые отрезки слева от
(включая его) и все чёрные отрезки слева от
(включая
его). Оставшиеся белые отрезки (их хотя бы
) не пересекаются с выкинутыми
чёрными; отсюда уже следует, что
Положим
и
тогда осталось белых и
чёрных отрезков. Рассмотрим любые
оставшихся белых и
оставшихся чёрных отрезков.
Если среди них нет пересекающихся, то, добавив к ним все выкинутые чёрные отрезки, получим набор из
белых
и
чёрных отрезков исходного набора, среди которых нет пересекающихся; это невозможно. Значит, оставшийся набор удовлетворяет
условию для новых чисел и
при этом в нём меньше отрезков, чем в исходном, поэтому
Противоречие.
Ошибка.
Попробуйте повторить позже
Дано натуральное Маша записывает по кругу
натуральных чисел. Далее Тая делает такую операцию: между каждыми двумя
соседними числами
и
она пишет некоторый делитель числа
больший 1; затем Тая стирает исходные числа и получает новый
набор из
чисел, стоящих по кругу. Всгда ли Тая может выполнять операции таким образом, чтобы через несколько операций все числа
оказались равными?
Источники:
Подсказка 1
Предположим, все числа в круге одинаковой чётности. Что можно сказать о чётности суммы любых двух соседних чисел?
Подсказка 2
В случае, когда все числа нечётные, Тая может победить. Можно ли какие-либо ситуации свести к данной?
Подсказка 3
Допустим, что ни одна сумма соседних чисел не является степенью двойки, как свести данную ситуацию к нечётным числам?
Подсказка 4
Пусть среднее арифметическое s всех чисел не является степенью двойки. Рассмотрим операцию: заменить каждое число на сумму соседей. Можно ли с её помощью уравнять числа в круге?
Подсказка 5
Лемма: После k таких операций числа становятся близки к s · 2ᵏ. Для любого ε > 0 при достаточно большом k все числа попадут в интервал (s − ε)·2ᵏ, (s − ε)·2ᵏ). Как выбрать ε, чтобы этот интервал не содержал целых степеней двойки?
Подсказка 6
Если в наборе есть пара (a, b) с суммой a + b = 2ᵏ (k ≥ 2), мы можем выбрать для неё делитель либо 2, либо 4.
При выборе 2 новое среднее s₁
При выборе 4 новое среднее s₂ = s₁ + 2/n
Почему числа s₁ и s₂ не могут одновременно быть степенями двойки? Может ли Тая победить в данной ситуации?
Подсказка 7
Что делать, если в начальном наборе есть 1?
Будем наращивать множество ситуаций, в которых Тая побеждает (т.е. сможет получить равных чисел).
(1) Пусть у нас нечётных чисел. Тогда за одну операцию можно получить
двоек.
(2) Пусть никакая сумма двух соседних чисел не является степенью двойки. Тогда за одну операцию можно получить ситуацию (1).
(3) Пусть среднее арифметическое всех чисел не равно степени двойки. Покажем, что сможем прийти к ситуации (2). Воспользуемся
следующей леммой.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Пусть
…,
— вещественные числа,
их среднее арифметическое. За один ход меняем набор
…,
на
Тогда для любого через несколько ходов все числа будут лежать в интервале
Доказательство леммы. Сделаем переобозначения, пусть
— данные числа, так что
Пусть
Ясно, что после хода не увеличится. Достаточно понять, что через некоторое количество
ходов этот максимум
отклонения станет не более
для некоторого фиксированного
Ниже увидим, что можно положить
и
Через ходов у нас будет набор
…,
где
Так как
имеем
Отсюда
Аналогично все
что завершает доказательство леммы.
_________________________________________________________________________________________________________________________________________________________________________________
Ясно, что Выберем
так, чтобы интервал (
) целиком помещался между соседними степенями
двойки:
для некоторого натурального Будем проводить много раз операцию замены пары соседей на их сумму. Тогда, согласно лемме,
найдётся
такое, что после
операций все числа будут лежать в интервале
а значит, в интервале между соседними степенями двойки и
Значит, после
операции выполнялось условие
(2).
(4) Пусть все числа не меньше 2. Если мы не в ситуации (2), то есть пара соседей сумма которых равна
где
—
натуральное. Попробуем сделать следующую операцию произвольно, только
и
заменим на число 2. Пусть в такой попытке мы не
пришли в ситуацию (3), то есть получили ситуацию, в которой среднее арифметическое
равно степени двойки. Тогда сделаем другую
попытку, в которой все пары меняются так же, только
и
заменяются на 4. По сравнению с первой попыткой
увеличилось на
поэтому мы окажемся в ситуации (3).
(5) Пусть набор исходных чисел произвольный. Тогда после одной операции замены пары чисел на сумму имеем ситуацию (4).
да
Ошибка.
Попробуйте повторить позже
Даны натуральные числа и
такие, что
Существует ли многочлен
степени больше
с коэффициентами из множества
такой, что
делится на
Источники:
Подсказка 1:
Как известно, для целочисленного многочлена P выражение P(a) − P(b) кратно a − b. Если подобрать такой многочлен P, что P(b) = a − b, задача будет решена.
Подсказка 2:
Как насчёт того, чтобы рассмотреть a − b в системе счисления с основанием b?
Легко видеть, что если то всякий многочлен с коэффициентами от 0 до
является нулевым.
Пусть Представим
в
-ичной записи (иными словами, в системе счисления с основанием
):
где
Поскольку
в этой записи
Покажем, что удовлетворяет условию. Действительно, по теореме Безу, для любого многочлена
с целыми коэффициентами
делится на
Значит,
делится на
Но тогда и
делится на
Существует при
Ошибка.
Попробуйте повторить позже
У школьников есть стопка из
карточки, которые пронумерованы числами от
до
Первый школьник перемешивает стопку,
затем берет сверху из получившейся стопки по одной карточке, и при каждом взятии карточки (в том числе при первом) записывает на
доску среднее арифметическое чисел на всех взятых им на данный момент карточках. Так он записывает
чисел, а когда в стопке
остается одна карточка, он возвращает карточки в стопку, и далее все то же самое, начиная с перемешивания стопки,
проделывает второй школьник, потом третий, и т.д. Докажите, что среди выписанных на доске
чисел найдутся два
одинаковых.
Источники:
Подсказка 1
Попробуйте посмотреть, какие множества чисел могут получаться у школьников на 1 шаге, на 2 шаге, на 100 шаге?
Подсказка 2
Попробуйте в явном виде найти все возможные значения, находящиеся в этих множествах. Как найти одинаковые среди них?
Подсказка 3
Рассмотрите первое, второе и сотое множества, а именно их объединение. Сколько в нëм чисел?
На -м шаге у каждого из
человек было выписано одно из чисел множества
На -м шаге — одно из чисел множества
На -м шаге выписано одно из чисел множества
где — сумма всех чисел (а вычитается — число на оставшейся в конце карточке).
Видим, что так что
Далее,
но числа
принадлежат
значит,
Итак, мы показали, что чисел, выписанных на
-м,
-м и
-м шагах, могут принимать не более
различных значений.
Следовательно, какие-то два из них равны.
Ошибка.
Попробуйте повторить позже
Дано число Положительные числа
…,
удовлетворяют условиям
и
Найдите наименьшее возможное значение выражения
Источники:
Подсказка 1
Для начала попробуйте угадать ответ. Поможет его угадать условия на выражения. На самом деле достаточно найти самые тривиальные x_i для которых условие верно.
Подсказка 2
И правда ответ n + a². Теперь попробуйте переписать сумму квадратов x_i через сумму квадратов 1 - x_i для того, чтобы избавится от n в правой части.
Подсказка 3
Теперь нам достаточно доказать, что сумма квадратов (1 - x_i) больше, чем (1 - a)^2. Тут надо рассмотреть два случая. Попробуйте понять почему при x₀ ≤ a задача очевидна, где x₀ — минимальное из x_i.
Подсказка 4
Если же x₀ ≥ a, то попробуйте из каждого слагаемого вынести соответственное x_i и оценить его a.
Будем доказывать ответ Заметим, что при
и
достигается равенство. Перепишем
Поэтому достаточно доказать, что
Пусть — наименьшее из чисел. При
имеем
Пусть то
Так как а значит, скобки из суммы неотрицательны. Следовательно,
Что и требовалось.
Ошибка.
Попробуйте повторить позже
Квадрат разбит на квадраты
Потом его разбивают на доминошки (прямоугольники
и
Какое наименьшее
количество доминошек могло оказаться внутри квадратов разбиения?
Источники:
Подсказка 1:
Нам необходимо сделать оценку снизу, то есть предъявить набор доминошек (возможно, просто доказать его существование), которые точно попадут в квадраты разбиения. Подумайте, как можно "ловить" подобные доминошки?
Подсказка 2:
Находить их в явном виде плохо, это просто не сделать (разбиений на домино очень много). Значит, нужно найти некоторые объекты, которые будут их "детектировать", то есть просто говорить, что они точно есть. Подумаем, какие самые тривиальные детекторы могут быть?
Подсказка 3:
Например, угловые клетки. В каждом углу доски нужная доминошка точно найдётся. Попробуем выделить несколько более высокоуровневые признаки. Почему доминошка, которая задевает угловую клетку, подходит?
Подсказка 4:
Потому что пересекает границу квадрата с нечётной стороной, а все такие границы лежать внутри квадратов разбиения, значит, такие доминошки всегда попадают в квадраты. Хм, что же хочется сделать?
Подсказка 5:
В такие моменты полезно попробовать обобщить идею! Как же будет звучать наше предположение?
Подсказка 6:
Для каждого квадрата с нечётной стороны, который исходит из левого нижнего угла, найдётся доминошка на его границе. Таким образом, мы сможем найти 50 нужных доминошек.
Подсказка 7:
Теперь нужно доказать, что для любого квадрата такая доминошка найдётся. Сделайте это самостоятельно, но скажем следующее: квадраты нечётные, а в доминошке ровно 2 клетки).
Подсказка 8:
Итого, мы нашли 50 требуемых доминошек. Кажется, можно найти больше...
Подсказка 9:
Осознайте, каким образом можно найти ещё 50 доминошек. Итого, есть оценка на 100 доминошек. Может, можно ещё больше?
Подсказка 10:
Спустя несколько попыток Вы, скорее всего, потерпели неудачу. Может, тогда пора переходить к примеру?
Подсказка 11:
Пример за Вами, однако скажем, что он достаточно "однородный"... Успехов!
Пример. Верхнюю и нижнюю горизонтали разобьём на горизонтальные доминошки — они окажутся в квадратах Остальной
прямоугольник
разобьём на вертикальные доминошки — они не окажутся в квадратах
Оценка. Рассмотрим квадраты
размеров
у которых левый нижний угол совпадает с левым
нижним углом исходного квадрата
Для каждого из квадратов
найдётся доминошка
пересекающая его
сторону (поскольку квадраты нечётной площади не разбиваются на доминошки). Легко видеть, что
лежит внутри квадратика
из разбиения. Аналогично, рассматривая квадраты
размеров
у которых
правый верхний угол совпадает с правым верхним углом исходного квадрата
находим ещё
нужных нам
доминошек
(
Это завершает решение (очевидно, что все доминошки
различны).
100



