№14 из ЕГЭ 2017
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
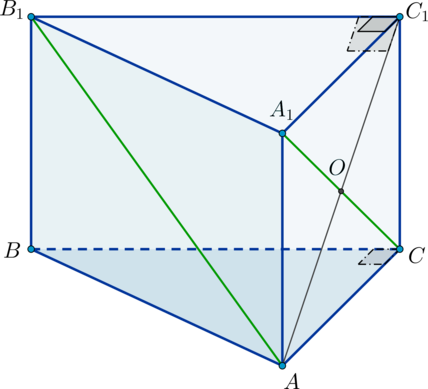
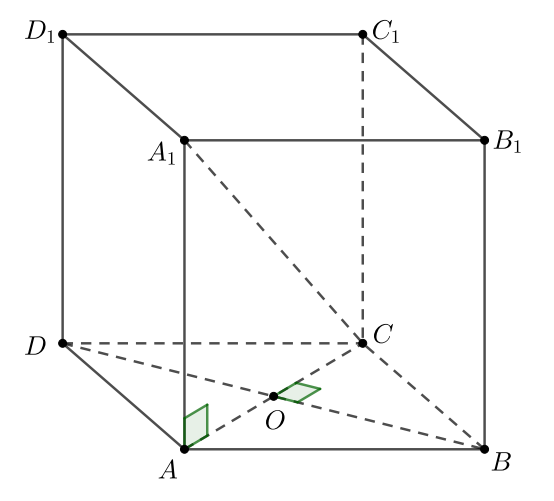
Дан прямоугольный параллелепипед Через прямую
параллельно прямой
проведена плоскость
причем сечение параллелепипеда плоскостью
представляет собой ромб.
а) Докажите, что — квадрат.
б) Найдите угол между плоскостью и плоскостью
если
и
Источники:
а) Заметим, что отрезки и
пересекаются и своей точкой пересечения делятся пополам по свойству параллелепипеда.
Обозначим их точку пересечения за
Следовательно,
лежит и в плоскости
и в плоскости
Проведем в
плоскости
прямую
через точку
параллельно
Значит,
— середина
— середина
Так как по признаку прямая параллельна плоскости, когда она параллельна некоторой прямой из этой плоскости, то прямая
параллельна любой плоскости, проходящей через
Следовательно, плоскость
— это плоскость, проходящая через
прямые
и
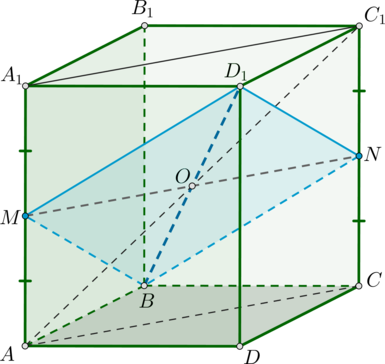
Соединив последовательно точки
получим сечение
По условию оно является ромбом,
следовательно,
Докажем, что Отсюда будет следовать, что
— квадрат. Это так, поскольку из того, что
прямоугольный параллелепипед, уже следует, что
— прямоугольник.
По теореме Пифагора и
Так как
как половины боковых ребер, а
по условию, то и
Что и требовалось доказать.
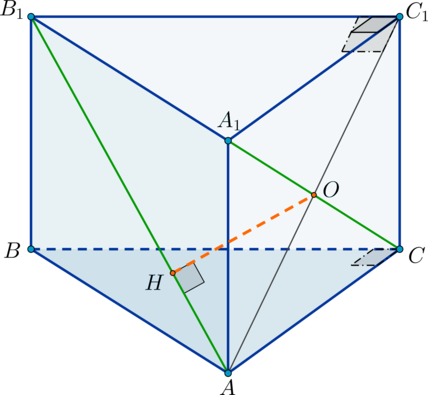
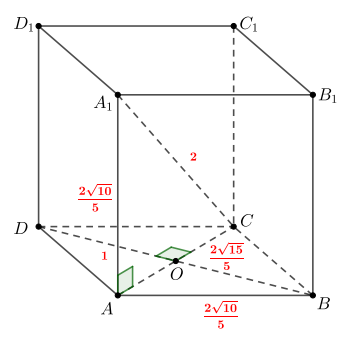
б) Проведем
— линия пересечения плоскостей
и
Заметим, что точка
будет лежать на
продолжении
за точку
Так как
то по теореме о трех перпендикулярах наклонная
тоже будет
перпендикулярна
Следовательно, построенный таким образом угол
и есть угол между плоскостями
и
Обозначим его за
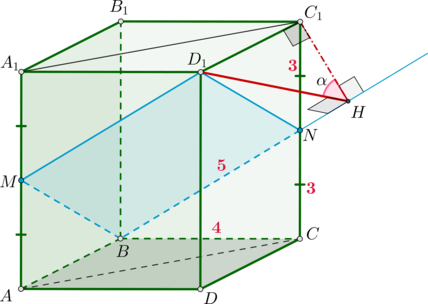
По теореме Пифагора из
Заметим, что
по двум углам, значит,
Отсюда находим, что Тогда из прямоугольного
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
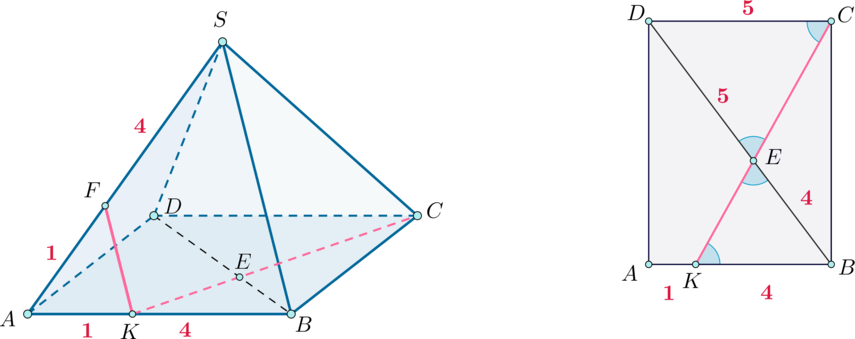
На ребрах и
треугольной пирамиды
отмечены точки
и
соответственно, причем
Точки
и
— середины ребер
и
соответственно.
а) Докажите, что точки
и
лежат в одной плоскости.
б) Найдите, в каком отношении эта плоскость делит объем пирамиды
Источники:
а) Докажем, что (отсюда будет следовать, что прямые
и
лежат в одной плоскости).
Так как по условию, то по теореме, обратной
теореме Фалеса,
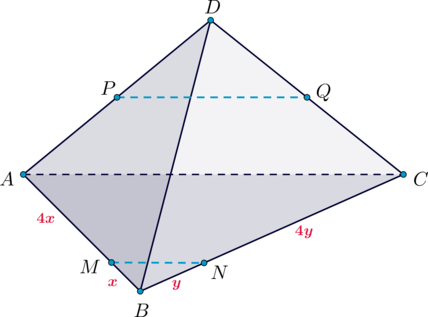
Так как
— середины
и
то
— средняя линия,
следовательно,
Следовательно,
Что и требовалось
доказать.
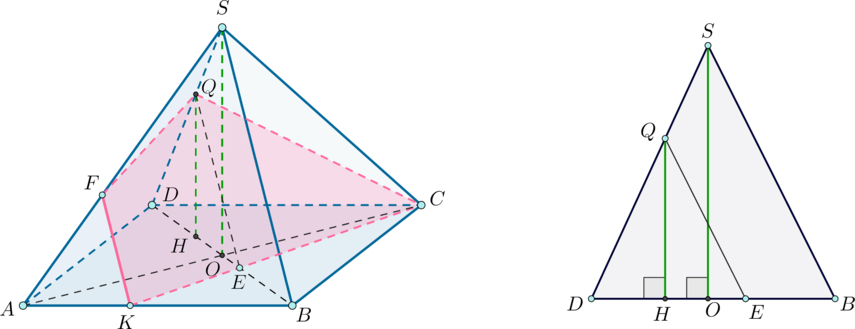
б) Отметим — середину
Рассмотрим пирамиду
Заметим, что
так как
а также так как
(две пересекающиеся
прямые
и
одной плоскости соответственно параллельны двум
пересекающимся прямым
и
другой плоскости, то такие плоскости
параллельны), то высота
пирамиды
относится к высоте
пирамиды
как
(пусть
).
Заметим также, что с коэффициентом 2 (так как
в два раза меньше
соответственно как средние линии в
).
Следовательно, Таким образом,
Значит,
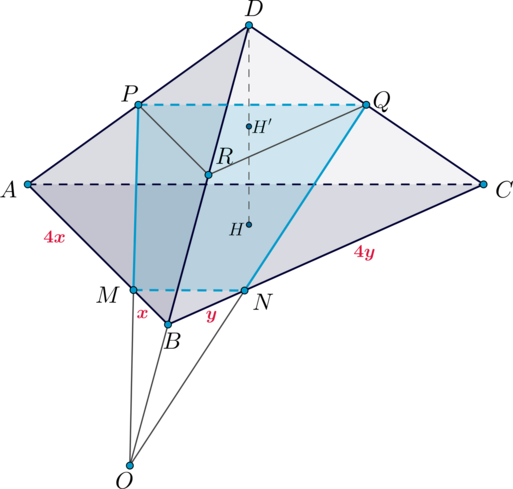
Заметим, что — усеченная пирамида, основания которой —
подобные треугольники
и
(
а
следовательно,
). Так как
и
то
Следовательно, Заметим, что высота
усеченной пирамиды
равна
Продлим
до пересечения в точке
Аналогично как с пирамидами и
высота пирамиды
относится к высоте пирамиды
как
Найдем отношение
Из подобия
Значит, пусть высота равна
тогда высота
равна
(отсюда следует, что
— высота усеченной пирамиды
то есть
).

Следовательно,
Значит,
Также
Следовательно,
Следовательно, объем всего многогранника отсекаемого от
пирамиды синей плоскостью, равен
Тогда объем пирамиды делится в отношении, равном
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой треугольной призмы является прямоугольный треугольник
причем
Диагонали
боковых граней
и
равны соответственно 26 и 10,
а) Докажите, что — прямоугольный.
б) Найдите объем пирамиды
Источники:
а) Так как
то по теореме о трех перпендикулярах
как наклонная. Следовательно,
— прямоугольный.
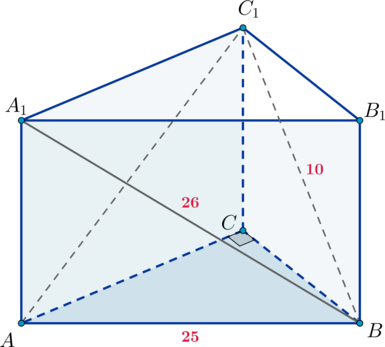
б) Заметим, что и
следовательно, по признаку
Тогда
— высота пирамиды
с основанием
Так как прямоугольный, то
По теореме Пифагора имеем:
Тогда искомый объем пирамиды равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида в основании которой лежит трапеция
с большим основанием
Известно, что
сумма углов
и
равна
Грани
и
перпендикулярны плоскости основания.
— точка пересечения
прямых
и
а) Докажите, что грани и
перпендикулярны.
б) Найдите объем пирамиды если известно, что
а высота пирамиды
равна
12.
Источники:
а) Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную второй плоскости. Так как
, то в плоскости
можно провести прямую
(тогда
). Аналогично в плоскости
можно
провести
(
). Следовательно, из одной точки к плоскости проведены две прямые, перпендикулярные ей, что
возможно только в том случае, если эти прямые совпадают, то есть
. Следовательно,
– общая прямая для двух плоскостей
и
. Следовательно,
совпадает с
.
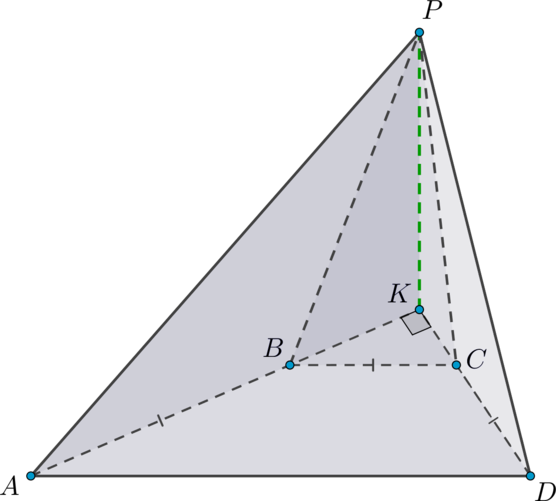
Таким образом, . Следовательно,
– высота пирамиды
.
Так как , то
. Следовательно,
и
, то есть
перпендикулярна двух
пересекающимся прямым из плоскости
, значит,
. Тогда плоскость
проходит через прямую,
перпендикулярную плоскости
, следовательно,
, чтд.
б) По теореме Фалеса
Следовательно, прямоугольный и равнобедренный, следовательно,
Тогда
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием четырехугольной пирамиды является прямоугольник
причем
Основанием
высоты пирамиды является центр прямоугольника. Из вершин
и
опущены перпендикуляры
и
на ребро
а) Докажите, что — середина отрезка
б) Найдите угол между гранями и
если
Источники:
а) Пусть — точка пересечения диагоналей прямоугольника
Тогда
— высота пирамиды. Так как диагонали прямоугольника равны и точкой
пересечения делятся пополам, то
Следовательно,
откуда
Обозначим
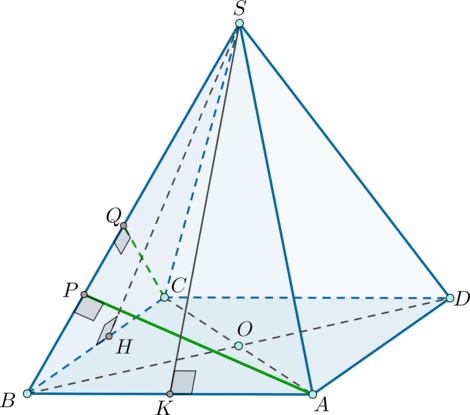
Рассмотрим грань Проведем
Тогда
Тогда
Рассмотрим грань Проведем
Тогда
Тогда
Следовательно, Что и требовалось доказать.
б) По условию В грани
имеем
так как
—
средняя линия в
Следовательно,
Тогда по определению
— линейный угол двугранного угла, образуемого гранями
и
Найдем его по теореме косинусов из
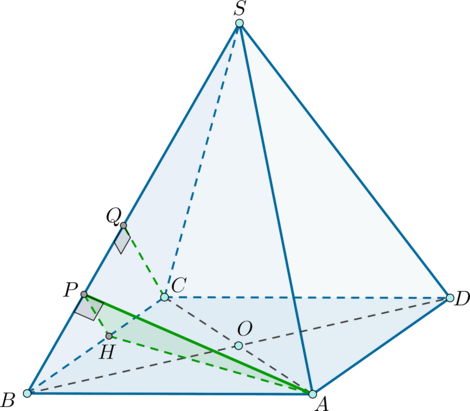
Так как то по теореме Пифагора из
По теореме Пифагора из
По теореме Пифагора из
Следовательно, по теореме косинусов из
Тогда угол между гранями и
равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
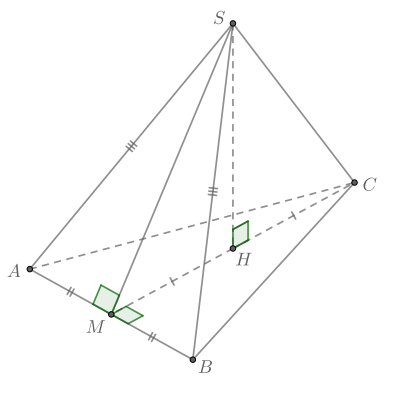
Основанием прямой треугольной призмы является прямоугольный треугольник
причем
Известно,
что прямая
перпендикулярна прямой
а) Докажите, что
б) Найдите расстояние между прямыми и
если известно, что
а) Заметим, что так как и
то
Следовательно, если
— наклонная, то
—
проекция этой наклонной на плоскость
Так как по условию наклонная перпендикулярна
то по теореме о трех перпендикулярах проекция
также
перпендикулярна
то есть
Следовательно, — прямоугольник, у которого диагонали взаимно перпендикулярны. Тогда это — квадрат, то есть
Что и требовалось доказать.
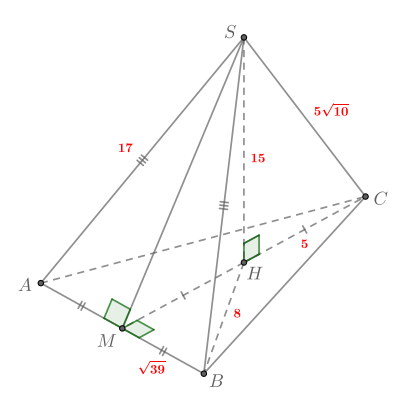
б) Из пункта а) следует, что так как
и
Следовательно,
перпендикулярна
любой прямой, лежащей в этой плоскости. Значит, если провести в этой плоскости прямую, перпендикулярную
то она будет
перпендикулярна и
и
Тогда по определению это и будет прямая, содержащая отрезок, равный расстоянию между
и
Поэтому проведем
Тогда
— искомое расстояние.
Заметим, что по двум углам, следовательно,
Так как из условия то и
Так как по доказанному
— квадрат со стороной
то диагональ
и
По теореме Пифагора для треугольника
По теореме Пифагора для треугольника
Тогда и окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде боковые рёбра
и
равны. Основанием высоты этой пирамиды является середина
медианы
треугольника
а) Докажите, что треугольник равнобедренный.
б) Найдите объём пирамиды если
а высота пирамиды равна 15.
Источники:
а) Треугольник равнобедренный, тогда его медиана
является высотой.
Пусть точка — середина
тогда
— высота пирамиды, то есть
перпендикулярна любой прямой из
плоскости
в частности,
Ранее мы поняли, что и следовательно, прямая
перпендикулярна плоскости
которую образую
прямые
и
Тогда прямая
перпендикулярна любой прямой из плоскости
в частности,
Точка лежит на медиане
треугольника
тогда в этом треугольнике медиана
совпадает с высотой,
следовательно,
— равнобедренный.
б) По теореме Пифагора для треугольника имеем:
По теореме Пифагора для треугольника имеем:
По теореме Пифагора для треугольника имеем:
Найдём площадь треугольника
Теперь, зная площадь основания пирамиды
мы можем найти её объём:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Ребро куба равно 6. Точки
и
— центры граней
и
соответственно.
а) Докажите, что — правильная пирамида.
б) Найдите объём
Источники:
a) Рассмотрим правильный тетраэдр В нём отрезки
и
— медианы боковых граней
и
— равных равносторонних треугольников. Следовательно,
то есть боковые ребра
пирамиды
paвны. Кроме того, в основании этой пирамиды лежит треугольник
образованный тремя равными
средними линиями равностороннего треугольника
Значит, основанием пирамиды
является равносторонний
треугольник, следовательно, пирамида правильная.
![]()
б) Найдём объём тетраэдра Рассмотрим плоскость
Прямая
перпендикулярна плоскости
следовательно, перпендикулярна и прямой
этой плоскости. Аналогично,
Значит, диагональ
перпендикулярна плоскости треугольника
Пусть
— точка пересечения диагонали
и плоскости
Значит,
— высота тетраэдра
Теперь найдём Для этого рассмотрим плоскость
Заметим, что точка
лежит в этой
плоскости. Тогда в плоскости
провёдем прямые
и
Пусть они пересекаются в точке
Рассмотрим треугольник
В нём
так как
Точка
— центр грани
значит,
![]()
Следовательно, — средняя линия
Значит,
и
— медианы
которые пересекаются в
точке
Медианы треугольника точкой пересечения делятся в отношении
считая от вершины. Значит,
Диагонали граней куба равны
А главная диагональ равна
Теперь мы можем найти объём тетраэдра
Так как треугольник образован средними линиями треугольника
и площадь
в четыре раза меньше
площади
а
— общая высота пирамиды
и тетраэдра
имеем:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На рёбрах и
треугольной пирамиды
отмечены точки
и
соответственно, причём
Точки
и
— середины ребер
и
соответственно.
a) Докажите, что точки
и
лежат в одной плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость разбивает пирамиду.
Источники:
a) Треугольник подобен треугольнику
по двум пропорциональным сторонам и углу между ними. В подобных
треугольниках соответственные углы равны, поэтому
, то есть
. Отрезок
является средней линией
треугольника
, значит,
. Тогда
, следовательно, точки
,
,
и
лежат в одной
плоскости.
![]()
б) Пусть объём равен
. Пятигранник
состоит из четырёхугольной пирамиды
с основанием
и треугольной пирамиды
с основанием
. Выразим их объемы через
.
Расстояние от до
вдвое меньше расстояния от
до
, а площади треугольников
и
относятся
как 1 к 6, так как
Также
Расстояние от точки до
вдвое меньше расстояния от
до
, поэтому
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой четырехугольной призмы является ромб
при этом
a) Докажите, что прямые и
перпендикулярны.
б) Найдите объем призмы, если
Источники:
а) Поскольку — прямая призма, то прямая
перпендикулярна плоскости
то есть
— проекция
на плоскость
Так как
— ромб, то прямые
и
перпендикулярны. Тогда по теореме о трех
перпендикулярах прямая
перпендикулярна прямой
б) Пусть
— точка пересечения
и
Объем призмы равен:
По теормеме Пифагора в треугольнике имеем:
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам, поэтому по теореме Пифагора в треугольнике
Приравняем выражения для и найдем
Теперь можем найти и объем призмы:
Следовательно, искомый объем призмы равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании пирамиды лежит прямоугольник
со стороной
и диагональю
Все боковые ребра
пирамиды равны 5. На диагонали
основания
отмечена точка
а на ребре
— точка
так, что
а) Докажите, что плоскость параллельна ребру
б) Плоскость пересекает ребро
в точке
Найдите расстояние от точки
до плоскости
Источники:
а) Продлим до пересечения с
в точке
Получим отрезок
по которому плоскость
пересекает грань
Рассмотрим основание пирамиды прямоугольник Так как
то
равнобедренный. Тогда
имеем:
Следовательно, тоже равнобедренный и
Отсюда
Заметим, что боковые грани и
представляют собой равносторонние треугольники со стороной 5. Таким образом, в
имеем
и
следовательно, он также равносторонний. Тогда
поскольку
как соответственные при секущей
Таким образом, в плоскости есть прямая
параллельная
Следовательно, по признаку плоскость
параллельна
б) Так как плоскость то она пересечет плоскость
по прямой
параллельной
В противном
случае
будет пересекать
следовательно, и плоскость
будет пересекать
Заметим, что так как все боковые ребра пирамиды равны, то высота упадет в точку пересечения диагоналей основания. Это
так, поскольку все треугольники
и
равны как прямоугольные по катету и гипотенузе, следовательно,
Проведем Так как
перпендикулярна плоскости
то и
Таким образом, необходимо найти
Рассмотрим Так как
то по теореме Фалеса:
Так как по двум углам, то
Найдем из прямоугольного
Тогда окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан куб , длина диагонали которого равна
. На луче
отмечена точка
так,
что
.
а) Докажите, что многогранник – правильный тетраэдр.
б) Найдите длину отрезка .
Источники:
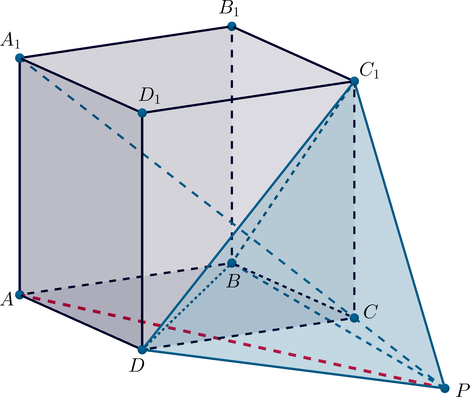
а) Так как , а
, то точка
находится на луче
за точкой
.
Правильный тетраэдр – правильная треугольная пирамида, все грани которой – равные треугольники.
Следовательно, нужно доказать, что все грани – равные равносторонние треугольники, то есть
доказать равенство
.
Так как диагональ куба в раз больше ребра куба, то ребро куба равно
. Так как
,
и
– диагонали граней куба, то каждая из них в
раз больше ребра куба, следовательно,
.
Найдем . Рассмотрим плоскость
. Так как
лежат в этой плоскости, то и вся прямая
в ней лежит, следовательно, и точка
.
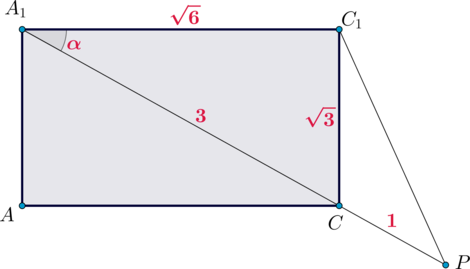
Найдем по теореме косинусов из
.
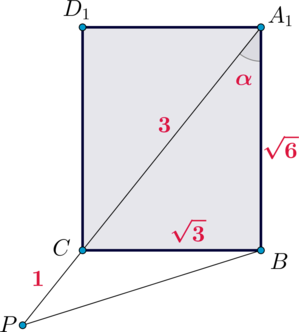
Аналогично рассмотрим плоскость
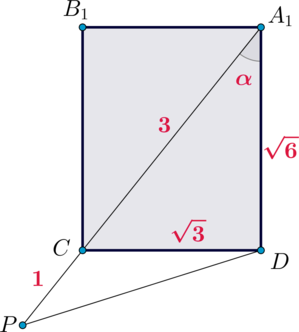
Таким образом, мы доказали, что
б) Рассмотрим плоскость :
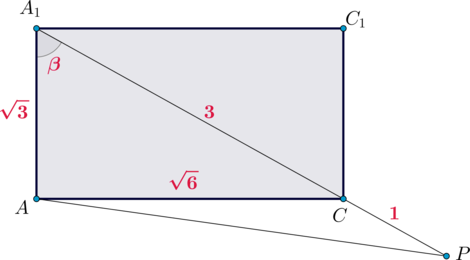
Найдем по теореме косинусов из
:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида , причем высота пирамиды, опущенная из точки
, падает в точку
. Известно, что
перпендикулярно
.
а) Докажите, что треугольник прямоугольный.
б) Найдите объем пирамиды , если известно, что
,
,
.
Источники:
а) Из условия следует, что – высота пирамиды. Следовательно,
и
. По
теореме о трех перпендикулярах так как наклонная
перпендикулярна прямой
, то и ее
проекция
перпендикулярна прямой
. Следовательно,
, то есть
прямоугольный.
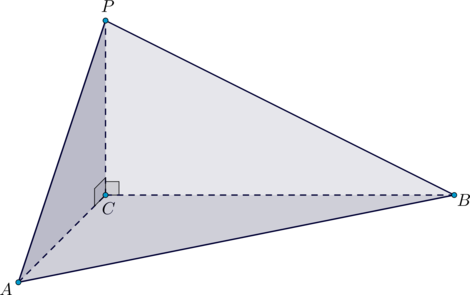
б) По теореме косинусов из :
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде с вершиной
все ребра
равны 5. На ребрах
,
,
взяты точки
соответственно,
причем
а) Докажите, что плоскость перпендикулярна ребру
б) Найдите расстояние от вершины до плоскости
Источники:
а) Построим сечение пирамиды плоскостью
Так как и
, то
Так как плоскость пересекает плоскость
по прямой
и
где
— линия пересечения
и
то плоскость
пересечет плоскость
по прямой, параллельной
Следовательно,
проведем
где
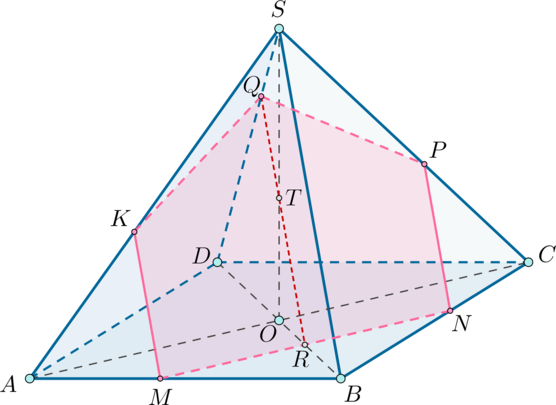
Пусть где
— высота пирамиды.
Так как то
по теореме Фалеса, следовательно,
Пусть Тогда пусть прямая
которая принадлежит
плоскости
пересечет
в точке
Получили
— сечение
пирамиды плоскостью
Заметим, что по теореме о трех перпендикулярах Действительно,
следовательно,
Значит, наклонная
Докажем, что Тогда
будет перпендикулярна двум
пересекающимся прямым плоскости
то есть перпендикулярна плоскости
Так как все ребра равны 5, то Следовательно,
—
прямоугольный и
По теореме о трех перпендикулярах так как
проекция
то и наклонная
Так как
по теореме
о трех перпендикулярах и
с
лежат в одной плоскости, то
Следовательно, раз
то и
то есть
Что и
требовалось доказать.
б) Так как то
— расстояние от точки
до плоскости
Так как и
то по теореме Фалеса
Так как
то
Так как
то
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



