Тема Регион 10 класс

Регион до 2015

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#74875Максимум баллов за задание: 7

Последовательность чисел $a ,a ,... 1 2$ задана условиями $a =1, 1$ $a = 143 2$ и

a1+a2-+...+-an an+1 = 5⋅ n

при всех $n ≥2.$ Докажите, что все члены последовательности — целые числа.

Источники: Всеросс., 2012, РЭ, 10.3(см. olympiads.mccme.ru)

Показать доказательство

Положим $S = a + a +...+a , n 1 2 n$ тогда $a =S − S . n+1 n+1 n$ Достаточно показать, что все числа $S n$ – целые. Заметим, что $S1 = 1,S2 = 144,$ и $5Sn- Sn+1 − Sn = n ,$ то есть $n+5 Sn+1 = n Sn.$ Значит, при $n≥ 2$

(n+ 5)(n+ 4)...⋅7 (n+ 5)(n+ 4)(n+ 3)(n+ 2)(n+ 1) Sn+1 =--n(n−-1)...⋅2--⋅S2 =--------6⋅5⋅4⋅3⋅2---------⋅144=

= (n-+5)(n-+4)(n-+3)(n-+2)(n+1)- 5

Так как одно из чисел $n+ 5,n +4,n+ 3,n +2,n+ 1$ делится на $5,$ то при $n ≥2$ число $Sn+1$ – целое.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#99946Максимум баллов за задание: 7

В языке племени АУ две буквы — $a$ и $y.$ Некоторые последовательности этих букв являются словами, причём в каждом слове не больше $13$ букв. Известно, что если написать подряд любые два слова, то полученная последовательность букв не будет словом. Найдите максимальное возможное количество слов в таком языке.

Источники: Всеросс., 2014, РЭ, 10.3(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Сколько существует слов длины n, которые состоят только из буквы a и у?

Подсказка 2

Верно, 2^n. Может ли в искомом множестве слов не быть слов длины 13?

Подсказка 3

Нет, потому что мы можем взять только слова длины 13, их количество больше, чем количество всех остальных слов. Как это соображение помогает построить пример?

Подсказка 4

Давайте возьмем в множество все слова длины хотя бы 7. Чему равно количество слов? Почему нельзя больше?

Подсказка 5

Количество слов равно 2¹⁴ - 2⁷ . Может ли в искомом множестве не быть слов длины 7?

Подсказка 6

Нет, не может. Пусть так же в языке есть k слов длины не больше 6. Докажите, что тогда количество не превосходит 2¹⁴ - 2⁷ - k.

Показать ответ и решение

Если все последовательности, количество букв в которых не меньше $7$ и не больше $13,$ являются словами, то, очевидно, условие задачи соблюдается; при этом количество таких слов равно $7 13 14 7 2 +...+2 = 2 − 2 .$ Осталось показать, что это количество — наибольшее возможное.

Общее количество последовательностей длины, не превосходящей $13,$ равно $2 13 14 2+2 + ...+ 2 =2 − 2.$ Если среди слов в языке нет ни одного $7$ -буквенного, то общее количество слов не превосходит $14 7 14 7 2 − 2− 2 <2 − 2.$ Пусть, напротив, в языке существует $7$ -буквенное слово $s.$ Тогда для каждого слова $t,$ состоящего из $6$ или менее букв, последовательность букв $st$ не может являться словом, и все последовательности вида $st,$ очевидно, различны. Значит, если в языке есть $k$ слов из $6$ или менее букв, то количество слов из хотя бы $7$ букв не превосходит $(7 13) 14 7 2 + ...+ 2 − k= 2 − 2 − k.$ Значит, общее количество слов не превосходит $(14 7 ) 14 7 k+ 2 − 2 − k =2 − 2,$ что и требовалось доказать.

Ответ:

$214− 27 =16256$

Ошибка.
Попробуйте повторить позже

Задача 3#106968Максимум баллов за задание: 7

По кругу стоят $101000$ натуральных чисел. Между каждыми двумя соседними числами записали их наименьшее общее кратное. Могут ли эти наименьшие общие кратные образовать $1000 10$ последовательных чисел (расположенных в каком-то порядке)?

Источники: Всеросс., 2014, РЭ, 10.7(см. olympiads.mccme.ru)

Показать ответ и решение

Пусть $n =101000.$ Обозначим исходные числа (в порядке обхода) через $a ,...,a ; 1 n$ мы будем считать, что $a = a. n+1 1$ Положим $bi = HOK (ai,ai+1).$ Предположим что числа $b1,...,bn$ — это $n$ подряд идущих натуральных чисел.

Рассмотрим наибольшую степень двойки $m 2 ,$ на которую делится хотя бы одно из чисел $ai.$ Заметим, что ни одно из чисел $b1,...,bn$ не делится на $m+1 2 .$ Пусть для определённости $.. m a1.2 ;$ тогда $.. m b1.2$ и $.. m bn.2 .$ Значит, $m b1 = 2 x$ и $m bn = 2 y$ при некоторых нечётных $x$ и $y.$ Без ограничения общности можно считать, что $x <y.$ Тогда, поскольку $b1,...,bn$ образуют $n$ последовательных чисел, среди них должно быть и число $m 2 (x +1)$ (поскольку $m m m 2 x <2 (x+ 1)< 2 y).$ Но это число делится на $m+1 2$ (так как $x +1$ четно), что невозможно. Противоречие.

Ответ:

Не могут

Ошибка.
Попробуйте повторить позже

Задача 4#81750Максимум баллов за задание: 7

Натуральные числа $a,b$ и $c,$ где $c≥2,$ таковы, что $1+ 1 = 1. a b c$ Докажите, что хотя бы одно из чисел $a+c, b+ c$ – составное.

Источники: Всеросс., 2013, РЭ, 10.6(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте, например, записать условие, что a + c составное, в другом формате, с которым проще работать.

Подсказка 2:

Если a + c составное, то НОД a и c больше 1 (почему?).

Подсказка 3:

Попробуйте преобразовать равенство из условия и подумайте, как к нему применить тот вывод про НОДы.

Показать доказательство

Достаточно показать, что хотя бы одно из двух чисел $d = (a,c) a$ и $d = (b,c) b$ больше $1.$ Действительно, если, например, $d > 1, a$ то $a+ c$ делится на $da$ и $a+c >$ $da,$ значит, $a+ c$ – составное число. Из условия следует, что $c(a +b)= ab;$ значит, $ab$ делится на $c.$ Но тогда, если $da = db =1,$ то и $c= 1,$ что противоречит условию.

Ошибка.
Попробуйте повторить позже

Задача 5#96956Максимум баллов за задание: 7

Дан выпуклый шестиугольник $ABCDEF.$ При этом оказалось, что $∠FAE = ∠BDC,$ а четырехугольники $ABDF$ и $ACDE$ являются вписанными. Докажите, что прямые $BF$ и $CE$ параллельны.

Источники: Всеросс., 2012, РЭ, 10.2(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

В этой задаче нужно просто собрать информацию про рисунок. У вас есть два вписанных четырëхугольника, посмотрите на вписанные углы и посчитайте углы для нужной параллельности.

Подсказка 2

Для удобства стоит отметить точку пересечения AE и BF.

Показать доказательство

$PIC$

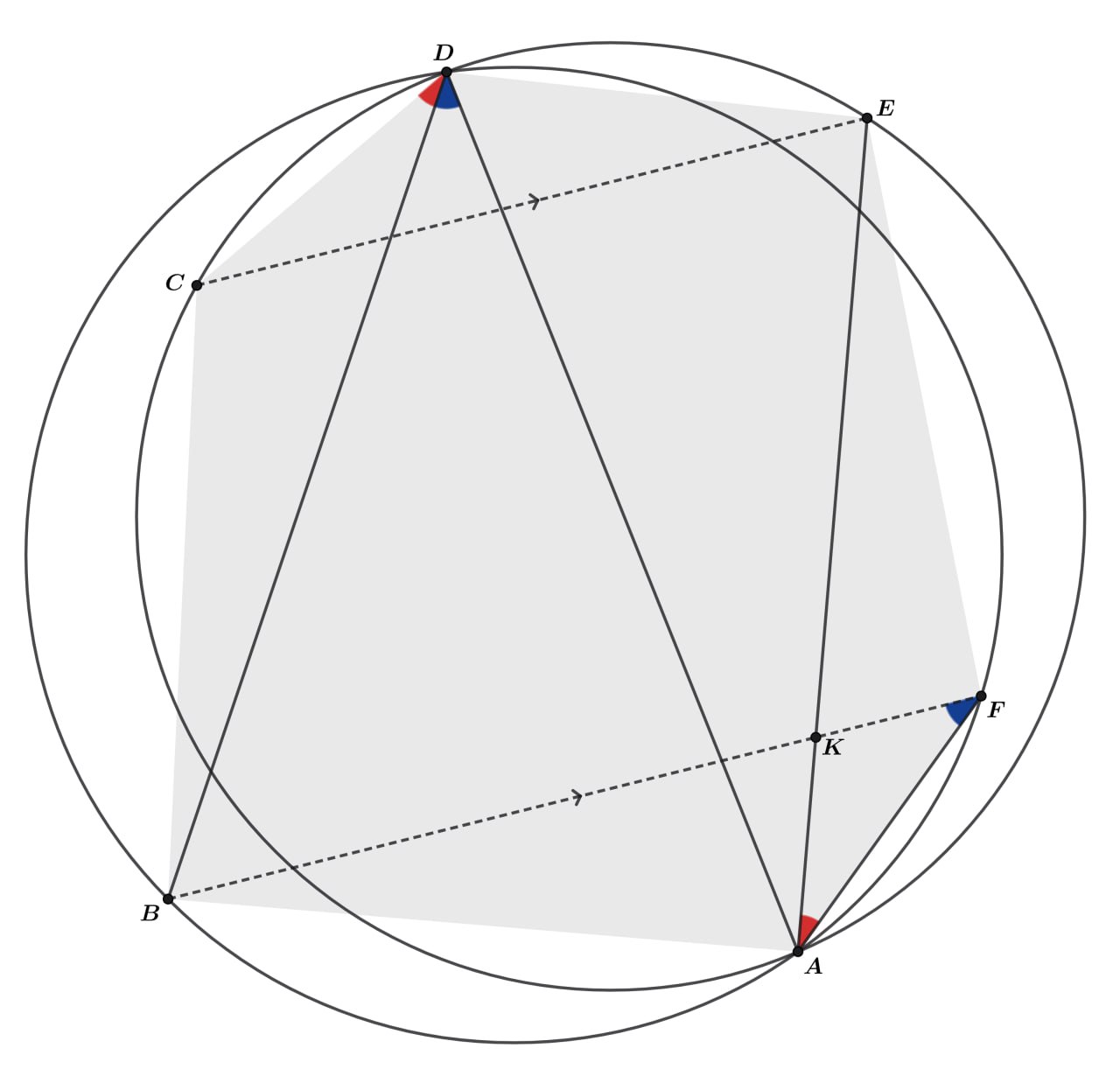
Пусть $K$ — точка пересечения отрезков $AE$ и $BF.$

∠AKB = ∠AF B+ ∠FAE = ∠ADB + ∠BDC = ∠ADC =∠AEC

Это и значит, что $BF ∥ CE.$

Ошибка.
Попробуйте повторить позже

Задача 6#82160Максимум баллов за задание: 7

В трапеции $ABCD$ боковая сторона $CD$ перпендикулярна основаниям, $O$ – точка пересечения диагоналей. На описанной окружности треугольника $OCD$ взята точка $S,$ диаметрально противоположная точке $O.$ Докажите, что $∠BSC = ∠ASD.$

Показать доказательство

$PIC$

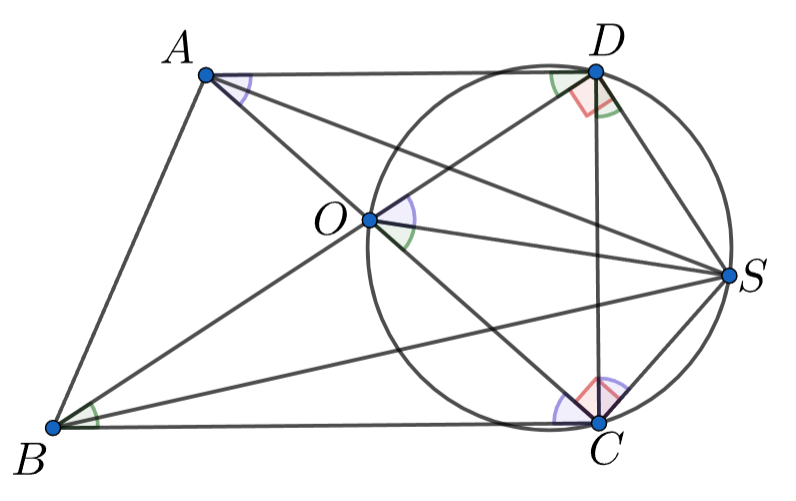
По условию $SO$ — диаметр, откуда $∘ ∠SCO = ∠SDO = 90.$ Отсюда получаем, что

∠ADB =∠SDC = ∠SOC

∠ACB = ∠SCD = ∠SOD

Заметим, что для решения задачи достаточно показать, что $∠DSB = ∠CSA.$ Это равносильно подобию треугольников $BDS$ и $ACS.$ Следовательно, достаточно показать, что $DSSC-= BADC.$ В окружности $(DOC )$ отрезки $DS$ и $SC$ стягиваются углами $DOS$ и $SOC,$ то есть

DS- = sin∠DOS-= sin-∠ACB- SC sin∠SOC sin∠ADB

Из прямоугольных треугольников $BDC$ и $ADC$ имеем $BD = DC ⋅sin∠DBC, AC =DC ⋅sin∠DAC.$ Таким образом,

BD-= sin∠DBC--= sin∠ADB--= DS- AC sin∠DAC sin∠ACB SC

Получили требуемое.

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#96366Максимум баллов за задание: 7

Ненулевые числа $a,$ $b,$ $c$ таковы, что $ax2+ bx +c> cx$ при любом $x.$ Докажите, что $cx2− bx+ a> cx − b$ при любом $x.$

Источники: Всеросс., 2010, ЗЭ, 10.5(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Посмотрите на выражения в неравенствах как на квадратные трëхчлены относительно x.

Подсказка 2

Осталось вспомнить, в каких случаях квадратный трëхчлен может целиком лежать выше оси абсцисс.

Показать доказательство

Если квадратный трёхчлен $ax2+ (b− c)x+ c> 0$ при всех $x,$ то это значит, что его дискриминант $(b− c)2− 4ac< 0.$ Ещё мы можем понять, что $c >0,$ подставив $x =0.$ Нас же просят доказать, что дискриминант трёхчлена $2 (b+ c) − 4c(a+ b)$ также меньше $0.$ Если заметить, что $2 2 (b+c) − 4bc= (b− c),$ то становится ясно, что второе неравенство идентично первому. Тогда получаем, что у графика трёхчлена ветви направлены вверх и его дискриминант отрицательный. Значит, неравенство верно.

Ошибка.
Попробуйте повторить позже

Задача 8#102029Максимум баллов за задание: 7

В кубе $ABCDA B C D 1 1 1 1$ площадь ортогональной проекции грани $AA B B 1 1$ на плоскость, перпендикулярную диагонали $AC , 1$ равна $1.$ Найдите площадь ортогональной проекции куба на эту плоскость.

Подсказки к задаче

Подсказка 1

Очевидно, что плоскость можно выбрать любую, так давайте выберем удобную! Рассмотрите плоскость, проходящую через центр куба. Что тогда будет являться проекцией грани AA₁B₁B? Что получится при проекции куба?

Подсказка 2

Проекций куба будет правильный шестиугольник. Посмотрите на вершины этого шестиугольника. Из них 3 это образы грани AA₁B₁B. Куда перешла четвертая вершина?

Показать ответ и решение

Выберем плоскость проекции так, чтобы она проходила через центр куба. Сечением куба этой плоскостью является правильный шестиугольник $MNKLP Q.$

$PIC$

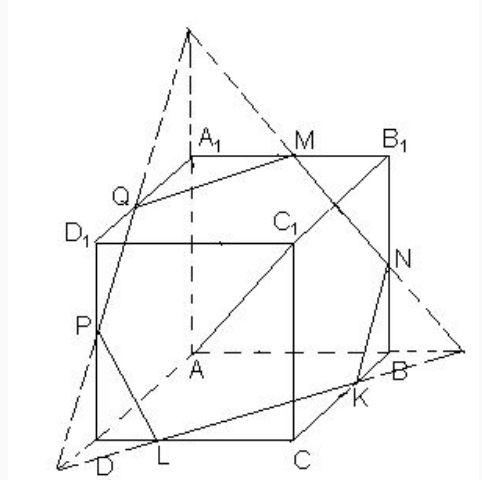
Проекцией куба на эту плоскость является шестиугольник $A′1B1B′C′D′D ′1,$

$PIC$

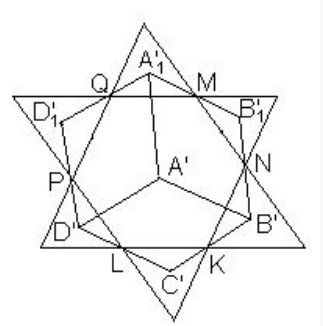
вершины которого являются центрами правильных треугольников, построенных на сторонах шестиугольника $MNKLP Q,$ поэтому полученный шестиугольник также является правильным, причём вершины $A$ и $C1$ куба проектируются в его центр. Проекцией грани $AA1B1B$ является параллелограмм $′ ′ ′ ′ A A1B1B.$ Его площадь в три раза меньше площади проекции куба.

Ответ:

$3$

Ошибка.
Попробуйте повторить позже

Задача 9#88926Максимум баллов за задание: 7

Арифметическая прогрессия $a ,a,..., 1 2$ состоящая из натуральных чисел, такова, что при любом $n$ произведение $a ⋅a n n+31$ делится на $2005.$ Докажите, что все члены этой прогрессии делятся на $2005.$

Источники: Всеросс., 2005, РЭ, 10.5(см. math.ru)

Показать доказательство

По условию числа $a ⋅a n n+31$ и $a ⋅a n+31 n+62$ делятся на $2005.$ Значит, их разность $a (a − a )=62da n+31 n+62 n n+31$ кратна $2005.$ Следовательно, $dan+31$ делится на $2005.$ Аналогично на $2005$ делится $dan+32.$ То есть $2005$ делит разность $2 dan+32− dan+31 = d.$

Покажем, что $d$ также делится на $2005.$ Заметим, что $2005= 401⋅5.$ Если $2 d$ делится на $5,$ то и $d$ делится на $5.$ Аналогично с простым числом $401.$

По доказанному выше имеем: $2 an⋅an+31 = (a1+ d(n − 1))(a1+ d(n+ 30))≡ a1 (mod 2005).$ Таким образом, $2 a1$ кратно $2005,$ а значит $a1$ делится на $2005.$ Из делимости $a1$ и $d$ на $2005$ следует требуемое.

Ошибка.
Попробуйте повторить позже

Задача 10#80971Максимум баллов за задание: 7

Уравнение

n n−1 n−2 x +a1x + a2x +...+ an−1x+ an = 0

с целыми ненулевыми коэффициентами $a1,a2,...,an$ имеет $n$ различных целых корней. Докажите, что если любые два корня взаимно просты, то и числа $an−1$ и $an$ взаимно просты.

Источники: Всеросс., 2004, РЭ, 10.5(см. math.ru)

Показать доказательство

По теореме Виета $|a | n−1$ равен модулю суммы всевозможных произведений $n − 1$ чисел из наборов $x ,x ,...,x, 1 2 n$ а $|a | n$ равен модулю произведения всех корней. Покажем, что $|an−1|$ не делится на $xi.$ Для этого заметим, что $|an−1|=$ $|x2x3...xn$ $+$ $x1x3x4...xn+$ $...+x1x2...xi−1xi+1xi+2...xn$ $+$ $...+ x1x2...xn−1|≡$ $|x1x2...xi−1xi+1xi+2...xn| (mod xi).$ По условию все корни взаимно просты, отсюда и следует, что $|an−1|$ не делится ни на один из корней, но тогда он не имеет общих множителей с $|an|,$ что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 11#111173Максимум баллов за задание: 7

В выпуклом многоугольнике на плоскости содержится не меньше $m2+ 1$ точек с целыми координатами. Докажите, что в нём найдутся $m + 1$ точек с целыми координатами, которые лежат на одной прямой.

Источники: Всеросс., 2002, РЭ, 10.2(см. math.ru)

Подсказки к задаче

Подсказка 1

Ясно, что надо использовать принцип Дирихле. Попробуем использовать пары остатков по модулю m. Всего таких m². Какой вывод можно сделать?

Подсказка 2

Точно! Найдутся две пары остатков, в которых первые и вторые компоненты сравнимы по модулю m. То есть можно найти в многоугольнике пары (x,y), (z,w) такие, что (x-z) и (y-w) делятся на m. Как теперь получить нужное количество точек на прямой?

Показать доказательство

По принципу Дирихле среди $m2 +1$ точек с целыми координатами найдутся такие две точки $(k,l)$ и $(k,l), 1 1$ что $k≡ k m 1$ и $l≡ l. m 1$ Тогда точки

( (k1− k)i (l1− l)i) k +---m---,l+---m-- , 0≤ i≤m

имеют целые координаты и лежат на одном отрезке между точками $(k,l)$ и $(k1,l1).$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#31279Максимум баллов за задание: 7

Длины сторон многоугольника равны $a ,a ,...,a . 1 2 n$ Квадратный трехчлен $f(x)$ таков, что $f(a )=f (a + ...+ a ). 1 2 n$ Докажите, что если $A$ — сумма длин нескольких сторон многоугольника, $B$ — сумма длин остальных его сторон, то $f(A )=f(B).$

Источники: Всеросс., 2001, РЭ, 10.1(см. math.ru)

Подсказки к задаче

Подсказка 1

В данной задаче мы хотим доказать, что квадратный трехчлен обладает некоторой симметрией. Какой симметрий обладает парабола?

Подсказка 2

График квадратного трехчлена обладает осевой симметрией: f(x) = f(a - x) для некоторого фиксированного a. Как эта симметрия применима к нашей задаче?

Подсказка 3

Пусть S - сумма всех сторон многоугольника. Тогда нам дано, что f(a_1) = f(S - a_1).
Попробуйте подставить эти выражения в квадратный трехчлен в общем виде, и из частного случая симметрии найти общий случай симметрии.

Показать доказательство

Первое решение.

Из графика квадратного трехчлена видим, что $f(a)=f(b) ⇐ ⇒ a= b,$ либо $a$ и $b$ расположены на числовой оси симметрично относительно точки $x0$ — абсциссы вершины параболы, т.е при $a+ b= 2x0.$ Но для многоугольника $a1 <a2+ ...+ an,$ поэтому $a1+ a2+ ...+an =2x0.$ Тогда $A+ B = 2x0,$ значит, $f(A)= f(B).$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Переформулируем задачу в непрерывном виде $2 f(x)=ux + vx+ w$ , тогда нашлось такое $a∈ (0,S)$ ( $S = a1+ ⋅⋅⋅+ an$ , что $f(a)=f(S− a)$ , то есть

ua2+ va+ w= u(S− a)2+ v(S − a)+ w ⇐⇒ 2va+ 2uSa =uS2 +vS ⇐⇒

⇐ ⇒ 2a(v+ uS)= S(v +uS) (∗)

Может ли быть так, что $2a= S$ ? Нет, поскольку в многоугольнике хотя бы 3 стороны и выполнено неравенство ломаной — если вычесть из обеих частей $a$ , то остальные стороны будут образовывать ломаную, соединяющую начало и конец стороны, что соответствует длине $a$ . Но тогда $v +uS =0$ , далее $f(A )=f(B)⇐ ⇒ f(A )=f(S− A)$ , но подставляя это аналогично (*), получим $2A(v +uS)= S(v+ uS )$ , что выполнено из $v+ uS = 0$ , что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 13#99352Максимум баллов за задание: 7

По данному натуральному числу $a 0$ строится последовательность $a n$ следующим образом: $a = a2− 5, n+1 n$ если $a n$ нечётно, и $an, 2$ если $an$ чётно. Докажите, что при любом нечётном $a0 >5$ в последовательности $an$ встретятся сколь угодно большие числа.

Источники: Всеросс., 2000, РЭ, 10.6(см. math.ru)

Показать доказательство

Пусть число $a = 2k+ 1 n$ нечетно и больше $5.$ Тогда имеем

2 2 an+1 = (2k+1) − 5= 4k + 4k− 4

2 an+2 = 2k +2k− 2

a = k2+k − 1 n+3

При этом $an+3$ нечетно и, поскольку $k > 2,$ то $an+3 =k2+ k− 1> 2k+1 =an.$ Таким образом, $a0 <a3 < a6 < ...< a3m,$ поэтому при любом $n$ имеем $a3n ≥ n.$

Ошибка.
Попробуйте повторить позже

Задача 14#30791Максимум баллов за задание: 7

К натуральному числу $X$ приписали справа три цифры. Получившееся число оказалось равным сумме всех натуральных чисел от 1 до $X$ . Найдите, чему может равняться $X$ .

Источники: Всеросс., 1999, РЭ, 10.1(см. math.ru)

Показать ответ и решение

Пусть приписали число $n =abc$ , тогда $1000X+ n= X (X + 1)∕2$ , то есть $2000X +2n= X2 +X$ или $X(X − 1999) =2n∈ [0,1998]$ . Произведение неотрицательно, при этом $X >0$ , однако при $X ≥ 2000$ равенство невозможно, то есть возможно только $X = 1999$ , для $n =0$ , которое подходит в силу равносильности преобразований.

Ответ:

$1999$

Ошибка.
Попробуйте повторить позже

Задача 15#32701Максимум баллов за задание: 7

В остроугольном треугольнике $ABC$ через центр $O$ описанной окружности и вершины $B$ и $C$ проведена окружность $ω.$ Пусть $OK$ — диаметр окружности $ω,$ а $D$ и $E$ соответственно — точки её пересечения с прямыми $AB$ и $AC.$ Докажите, что $ADKE$ — параллелограмм.

Источники: Всеросс., 1998, РЭ, 10.2(см. math.ru)

Подсказки к задаче

Подсказка 1

Во-первых, в силу равенства OB=OC и того, что OK — диаметр, ∠BOK и ∠COK равны. А еще O,C,E,K,B лежат на одной окружности. Если это так, то какие вписанности это даёт? А что дают сами вписанности?

Подсказка 2

Это даёт равенство 180°-∠BOK = ∠CEK. А также равенство ∠KOB и ∠KDB. А что в силу этого можно сказать? Как это помогает в доказательстве того, что ADKE — параллелограмм?

Показать доказательство

В силу равенства $OB = OC$ и того, что $OK$ — диаметр, треугольники $OBK$ и $OCK$ равны как прямоугольные с равными катетами и общей гипотенузой. Отсюда с учетом того, что $O$ — центр описанной окружности треугольника $ABC,$ имеем:

∠BOC ∠COK = ∠BOK =---2- = ∠A =α

$PIC$

Дальше возможны случаи расположения точек $D,E$ на прямых в зависимости от соотношения сторон треугольника $ABC,$ но решение остаётся аналогичным.

Из вписанности четырехугольника $ODBK$ следует

∠KDB = ∠KOB =α = ∠EAD ⇒ AE ∥KD

Из вписанности четырехугольника $OCEK$ следует

∠CEK = 180∘− ∠COK = 180∘− α= 180∘− ∠EAD ⇒ EK ∥AD

Тогда $AEKD$ — параллелограмм по определению, так как его стороны попарно параллельны.

Ошибка.
Попробуйте повторить позже

Задача 16#73202Максимум баллов за задание: 7

Найдите все натуральные числа, имеющие ровно шесть делителей, сумма которых равна $3500.$

Показать ответ и решение

Запишем каноническое разложение натурального числа $n = pα1 ⋅pα2⋅...⋅pαk. 1 2 k$ Его количество делителей равно $(α + 1)(α + 1)...(α +1). 1 2 k$ Если это число равно $6,$ то либо $k= 1$ и $α1 = 5,$ либо $k= 2,α1 = 2,α2 = 1.$ То есть либо $5 n= p,$ либо $2 n = pq$ ( $p$ и $q$ — простые).

В первом случае $2 3 4 5 1 +p+ p + p +p + p = 3500,$ откуда $2 3 4 p(p+ p +p + p )=3499.$ Число $3499$ не делится на $2,3,5$ и $7,$ поэтому $p> 10,$ но в этом случае $2 3 4 p(p+ p +p + p )>3499.$ Поэтому это уравнение решений в простых числах не имеет.

Во втором случае $2 2 1+ p+ p +q +pq+ pq =3500,$ то есть $2 3 (1+ p+ p)(1+q)= 5 ⋅7⋅4.$ Первый множитель нечётен и не кратен $5$ (чтобы убедиться в этом, достаточно это утверждение проверить для соответствующих остатков). Отсюда, учитывая, что $2 1 +p+ p > 1,$ имеем $2 1+ p+p = 7.$ Значит, $p= 2,$ $q = 499.$ Числа $2$ и $499$ — простые. Искомое число $n =22⋅499= 1996.$

Ответ:

$1996$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#73365Максимум баллов за задание: 7

Известно, что свободный член $α 0$ многочлена $P(x)$ с целыми коэффициентами по модулю меньше 100, а $P(20)= P(16)=2016.$ Найдите $α0.$

Источники: Отборочный этап олимпиады БИБН - 2016 (адаптация задачи 10.6 с Регионального этапа ВсОШ - 1994)

Подсказки к задаче

Подсказка 1

Есть смысл рассматривать не многочлен P(x), а многочлен P(x) - 2016, ведь у него мы знаем два корня.

Подсказка 2

Понятно, что мы можем записать многочлен P(x) - 2016, как (x - 20)(x - 16)Q(x). Попробуйте выразить P(0).

Показать ответ и решение

Из условия следует, что

P(x)− 2016 =(x− 20)(x− 16)Q(x)

где $Q (x)$ — некоторый целочисленный многочлен.

Как известно, свободный член многочлена равен его значению в нуле. Тогда

P(0)= 2016+ 320Q (0)

Из условия

−100≤ 2016+ 320Q (0)≤ 100

получаем, что $Q(0)= −6,$ а свободный член равен $96.$

Ответ:

$96$

Ошибка.
Попробуйте повторить позже

Задача 18#83585Максимум баллов за задание: 7

Окружность с центром $O$ вписана в четырехугольник $ABCD$ и касается его непараллельных сторон $BC$ и $AD$ в точках $E$ и $F$ соответственно. Пусть прямая $AO$ и отрезок $EF$ пересекаются в точке $K,$ прямая $DO$ и отрезок $EF$ — в точке $N,$ а прямые $BK$ и $CN$ — в точке $M.$ Докажите, что точки $O,K,M$ и $N$ лежат на одной окружности.

Показать доказательство

Пусть вписанная окружность четырёхугольника $ABCD$ касается его стороны $AB$ в точке $P.$ Из точек $P$ и $E$ отрезок $OB$ виден под прямым углом, значит, эти точки лежат на окружности с диаметром $OB.$ Докажем, что на этой окружности лежит и точка $K.$ Действительно, поскольку $∠P OA$ — половина центрального угла $∠P OF$ вписанной окружности данного четырёхугольника, а $∠PEF$ — угол, вписанный в эту окружность, то $∠P OA= ∠P EF.$ Поэтому $∠POK = ∠PEK.$ Значит, точка $K$ лежит на окружности, проходящей через точки $P,O$ и $E,$ т.е. на окружности с диаметром $OB$ Из доказанного следует, что $∘ ∠BKO =90 .$ Аналогично докажем, что $∘ CND =90 .$ Значит, из точек $K$ и $N$ отрезок $OM$ виден под прямым углом. Следовательно, точки $O,K,M$ и $N$ лежат на окружности с диаметром $OM.$

$PIC$