17.06 Подобие треугольников и пропорциональные отрезки
Ошибка.
Попробуйте повторить позже
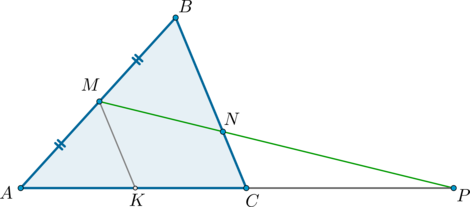
В треугольнике на середине стороны
отмечена точка
Точка
на продолжении стороны
за
точку
такова, что
Найдите меньший из отрезков, на которые прямая
делит сторону
если
Пусть — точка пересечения прямых
и
Способ 1.
По условию имеем:
Тогда по теореме Менелая для треугольника и прямой
Так как то искомый отрезок равен
Способ 2.
Проведем Тогда по теореме Фалеса точка
поделит
в том же отношении, что точка
поделит отрезок
Тогда
и так как
то
Заметим, что по двум углам, так как
— общий и
как соответственные. Тогда
имеем:
Отсюда получаем Далее, так как
— средняя линия в
то
Тогда окончательно
получаем
Очевидно, что так как отрезок
в таком случае равен
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В трапеции основания равны 18 и 12, а боковые стороны 15 и 12. Боковые стороны продолжили до взаимного пересечения. Найдите сумму длин отрезков, на которые продолжены боковые стороны.
Пусть дана трапеция ,
– основания,
– точка пересечения продолжений боковых
сторон. Обозначим
.

Тогда по двум углам:
– общий,
как соответственные при
и
секущей. Следовательно:
Ошибка.
Попробуйте повторить позже
Найдите отношение
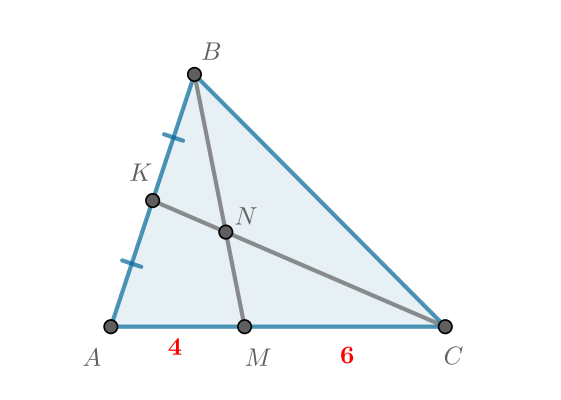
Проведем через прямую, параллельную
Пусть
— ее точка пересечения с

Тогда по теореме Фалеса для угла и секущих его параллельных прямых
и
Теперь рассмотрим теорему о пропорциональных отрезках для угла и секущих его параллельных прямых
и
Получили, что
Ошибка.
Попробуйте повторить позже
Найдите неизвестную сторону треугольника на картинке.
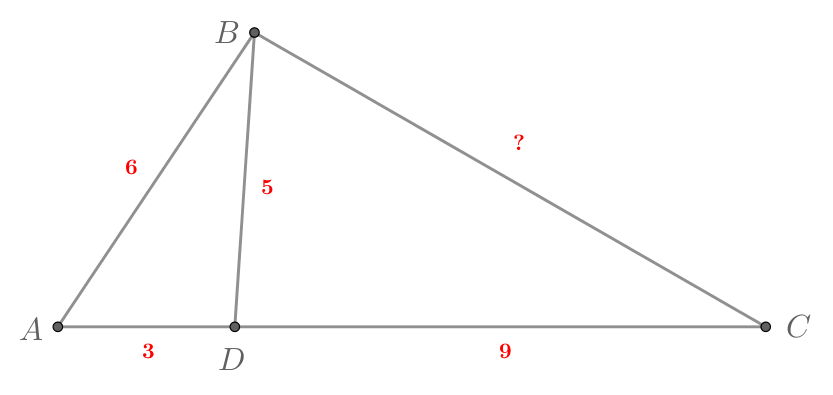
Рассмотрим треугольники и
. Они имеют общий угол
. Кроме того,
Таким образом, по отношению двух сторон и углу между ними. Найдем коэффициент подобия
этих
треугольников:
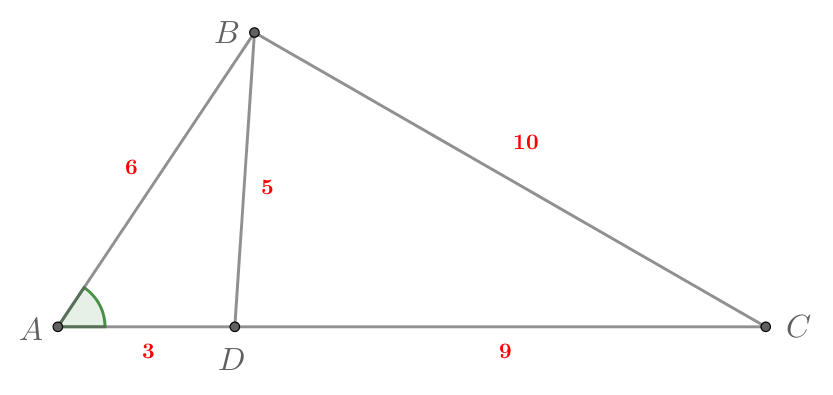
Тогда неизвестная сторона равна
Ошибка.
Попробуйте повторить позже
В треугольнике чевиана
делит сторону
на отрезки
и
Известно, что
Найдите
Рассмотрим треугольники и
Они имеют общий угол
углы
и
равны по условию. Таким образом,
по двум углам. Тогда коэффициент подобия
этих треугольников равен
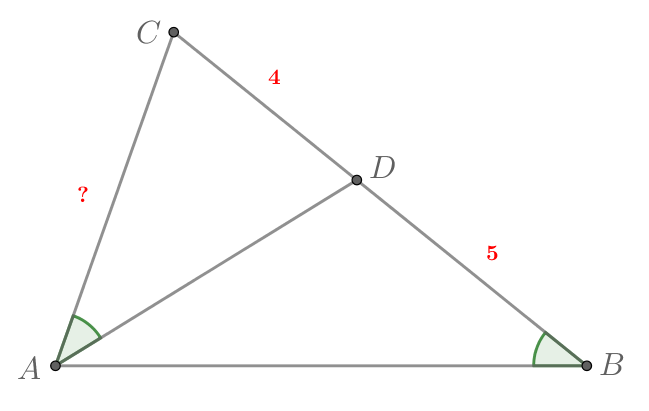
Отсюда найдем искомый отрезок:
Ошибка.
Попробуйте повторить позже
В параллелограмме точка
— середина
а точка
— середина
Найдите отношение длин отрезков, на
которые прямые
и
разделили диагональ
Пусть — точка пересечения
и
а
— точка пересечения
и
Так как у параллелограмма противоположные стороны равны, то Рассмотрим четырехугольник
В нем противолежащие стороны
и
параллельны и равны, следовательно, это параллелограмм и

Далее, и
следовательно, по теореме Фалеса
Кроме того, и
следовательно, по теореме Фалеса
Получили, что
Ошибка.
Попробуйте повторить позже
Окружность касается одного из катетов прямоугольного равнобедренного треугольника и проходит
через вершину противолежащего острого угла. Найдите радиус окружности, если ее центр лежит на
гипотенузе треугольника, а катет треугольника равен .
(Источник: Сборник задач по геометрии, И.Ф.Шарыгин, Р.К.Гордин)
В решении будем обозначать катет треугольника за . Пусть
– радиус окружности. Если
–
точка касания окружности с катетом
, то
. Рассмотрим рисунок:
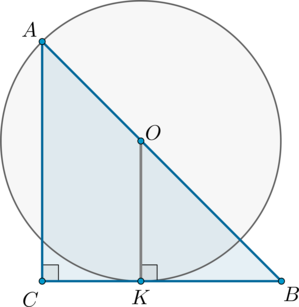
Заметим, что по двум углам , следовательно,
По теореме Пифагора
Тогда по теореме Пифагора из
Ошибка.
Попробуйте повторить позже
В треугольник вписан ромб таким образом, что один угол у них общий, а противоположная вершина
ромба лежит на стороне треугольника и делит ее на отрезки длинами и
. Найдите периметр
треугольника, если сторона ромба равна
.
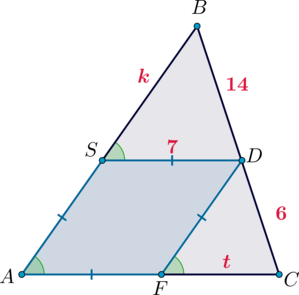
Рассмотрим рисунок. Так как по определению ромба , то
, следовательно,
. Следовательно, по двум углам (
у них общий)
. Обозначим
,
. Тогда имеем:
Аналогично и
. Следовательно,
Ошибка.
Попробуйте повторить позже
В квадрате на стороне
взята точка
такая, что
. Найдите
расстояние от точки
до прямой
.
Обозначим сторону квадрата за , тогда
,
. Необходимо найти
.
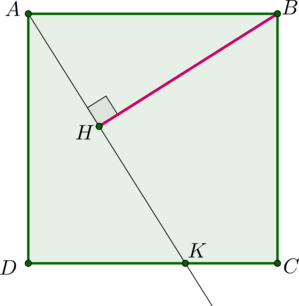
Заметим, что по двум углам (
,
как
накрест лежащие). Следовательно,
Ошибка.
Попробуйте повторить позже
В треугольник со стороной и высотой
, проведенной к этой стороне, вписан квадрат таким
образом, что две соседние вершины квадрата лежат на стороне
, а две другие вершины квадрата
лежат на двух других сторонах треугольника соответственно. Найдите периметр квадрата.
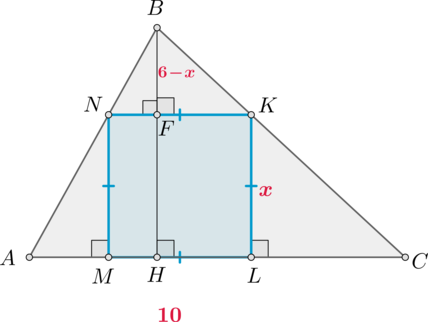
Рассмотрим рисунок.
Пусть ,
– высота,
– квадрат со стороной
. Необходимо найти
.
Так как , то
. Так как
и
, то
. Так
как отрезки параллельных прямых, заключенные между двумя параллельными прямыми,
равны, то
. Следовательно,
. Заметим, что
как
соответственные при
и
секущей. Следовательно,
по двум углам.
Значит,
Ошибка.
Попробуйте повторить позже
В треугольнике отрезок
— медиана, точка
лежит на
так, что
Отрезок
проходит через
точку
причём точка
лежит на стороне
Найдите отношение
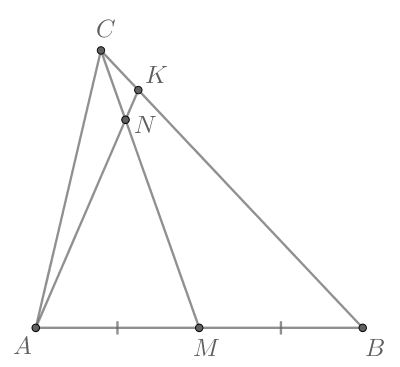
Построим

Обозначим
Способ 1.
Так как — средняя линия в треугольнике
то
Треугольники и
подобны по двум углам:
— общий,
как соответственные при
параллельных прямых и секущей, тогда
Так как то имеем:
Способ 2.
По теореме о пропорциональных отрезках для угла и секущих прямых
и
имеем:
По теореме о пропорциональных отрезках для угла и секущих прямых
и
имеем:
Тогда получаем
Способ 3.
Так как то
Кроме того,
так как точка
— середина
Тогда по
теореме Менелая для треугольника
и секущей
имеем:
Отсюда получаем
Ошибка.
Попробуйте повторить позже
Расстояния от точки , расположенной внутри прямого угла, до сторон угла равны 4 и 3. Через точку
проведена
прямая, отсекающая от угла треугольник, площадь которого равна 32. Найдите длину отрезка этой прямой,
заключенного внутри угла.
(МИОО 2013)
Пусть — вершина угла,
и
— точки пересечения прямой со сторонами угла,
— проекция
на
,
— проекция
на
.
— прямоугольник
,
. Обозначим
.
по двум углам. Запишем подобие
|
|
Тогда по условию
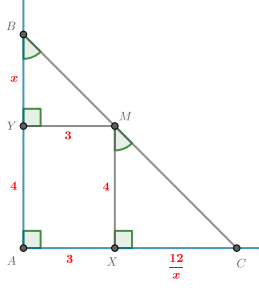
или
.
Ошибка.
Попробуйте повторить позже
В треугольнике проведены высоты
и
Найдите
если
и

Докажем, что треугольники и
подобны. Для этого рассмотрим прямоугольный треугольник
. В нем
Теперь рассмотрим прямоугольный треугольник . В нем также
Так как , то треугольники
и
подобны по отношению двух сторон и углу между ними. Тогда
коэффициент подобия
этих треугольников равен
Отсюда искомый отрезок равен
Ошибка.
Попробуйте повторить позже
В треугольнике проведены медианы
и
. На сторонах
треугольника
,
и
взяты соответственно точки
, причем
,
и
.
а) Докажите, что .
б) Найдите площадь треугольника , если площадь треугольника
равна 48.
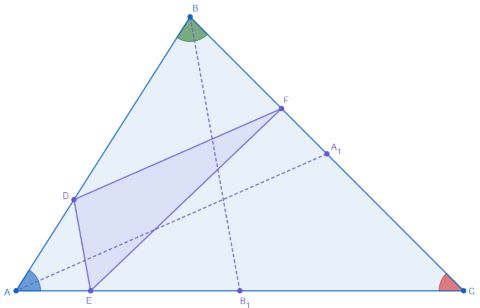
а) 1. Рассмотрим . Из условия задачи мы знаем, что
.
Используя теорему Фалеса, получаем:
Отсюда по правилу пропорции
2. Заметим, что – середина
и
3. Из двух предыдущих пунктов получаем, что:
Ч.Т.Д.
б) 1. Выразим площадь через площадь
:
2. , значит, по теореме Фалеса (помним, что
– середина
):
Иными словами:
3. Выразим площадь через площадь
:
4. Выразим площадь через площадь
:
5. Найдём :
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
На них из точек
и
опущены перпендикуляры
и
соответственно.
а) Докажите, что прямые и
параллельны.
б) Найдите отношение если
а)
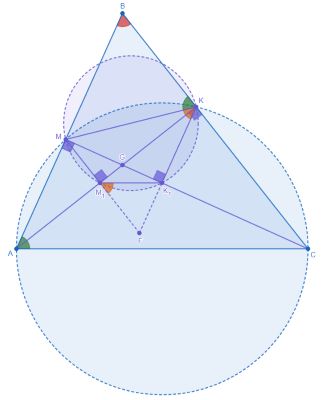
1. Треугольник по условию остроугольный, следовательно, основания его высот лежат на его сторонах.
2. Четырёхугольник — вписанный, поскольку
причём
и
лежат по одну сторону от
Раз так, то как вписанные, опирающиеся на одну
дугу.
3. Четырёхугольник — вписанный, поскольку
причём
и
лежат по одну сторону от
Раз так, то как вписанные, опирающиеся на одну
дугу.
4. и
— один и тот же угол, а значит,
5. Уже это тождество в свою очередь означает параллельность
поскольку
как соответственные при
Ч.Т.Д.
б)
1. Продлим и
до точки пересечения
2. Сумма противоположных углов во вписанном четырёхугольнике равна
Раз так, то
3. Однако и поскольку
и
—
смежные.
4. Из прошлых двух пунктов ясно, что
а
значит,
5. Коэффициент подобия равен отношению
—
прямоугольный, следовательно,
6. Абсолютно аналогичные действия проворачиваем и с и
доказывая их подобие и вычисляем коэффициент этого подобия
7. По сумме углов четырёхугольника
8. как вертикальные.
9. По сумме углов четырёхугольника
То есть
10. Найдём по ОТТ:
11. Пусть тогда из найденного отношения
а
То есть:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
А вот и вторая геометрическая задачка из воспоминаний Деда Мороза: Две
окружности разных радиусов пересекаются в точках и
причем их
центры лежат по разные стороны от хорды
Вне обеих окружностей
взята точка
лежащая по ту же сторону от хорды
что и центр
меньшей окружности. Прямая
пересекает меньшую окружность в
точках
и
а большую — в точках
и
Прямая
пересекает
меньшую окружность в точках
и
а большую — в точках
и
а) Докажите, что =
б) Найдите сумму произведений длин противоположных сторон четырехугольника
если
и
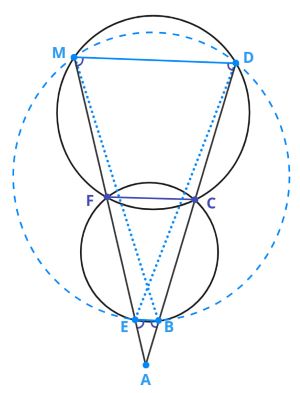
а) Вспомним теорему о двух секущих и распишем ее для обеих окружностей.
Для меньшей окружности справедливо:
откуда
Для большей окружности справедливо:
откуда
Из двух пропорций, в которых левые части одинаковы, выводим:
Ч.Т.Д.
б)
1. В пункте а) мы доказали равенство:
Из него по обратной теореме Фалеса следует, что и
2. Из подобия выводим равенства углов:
3. В условии пункта б) утверждается, что С учетом с
прошлых двух тождеств этот тезис дает понять, что
и
на самом
деле равнобедренные.
4. Отсюда получаем, что трапеция также равнобедренная. У любой
равнобедренной трапеции сумма противоположных углов равна
следовательно, она вписанная.
5. Для вписанного четырехугольника справедлива теорема Птолемея, гласящая о том, что сумма произведений длин противоположных сторон вписанного четырехугольника равна произведению длин его диагоналей, то есть
NOTA BENE: Заметим, что теоремы Птолемея нет в учебниках федерального перечня, поэтому перед её применением на ЕГЭ следует привести её доказательство.
Ошибка.
Попробуйте повторить позже
Дан равнобедренный треугольник, основание которого относится к боковой стороне как . Найдите
отношение, в котором точка касания вписанной в треугольник окружности и боковой стороны делит эту
боковую сторону.
Центр вписанной в окружности будет лежать на биссектрисе, проведенной к его основанию.
Пусть
– основание,
– биссектриса, следовательно, высота и медиана. Пусть
– точка
касания окружности и
. Необходимо найти, например,
.

Если обозначить ,
, то
. Заметим, что по двум углам
(
– общий, а также оба прямоугольные). Следовательно,
Ошибка.
Попробуйте повторить позже
и
– биссектрисы углом
и
соответственно треугольника
. На продолжениях
сторон
и
взяты точки
и
так, что
. Доказать, что
.
(Задача от подписчиков)
Пусть , а
. Тогда
и
. Так как
равнобедренный, то в нем
. Аналогично в
углы
.

. Следовательно, по двум углам
.
Следовательно,
Заметим, что тогда по двум углам (
,
по доказанному выше) и общей стороне. Следовательно,
,
. Значит, перемножив
равенства
и
, получим:
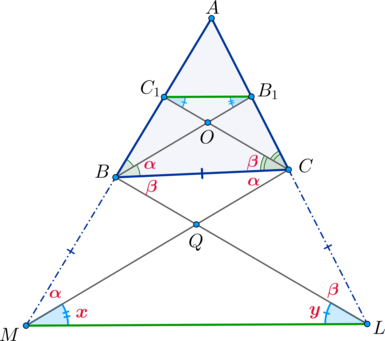
Следовательно, по двум пропорциональным сторонам (из
Но из
Ошибка.
Попробуйте повторить позже
Дан параллелограмм . Из вершины острого угла
проведены две прямые, делящие угол на
три равные части, причем одна пересекает сторону
в точке
, а другая – сторону
в точке
, причем
. Известно также, что
. Найдите
.
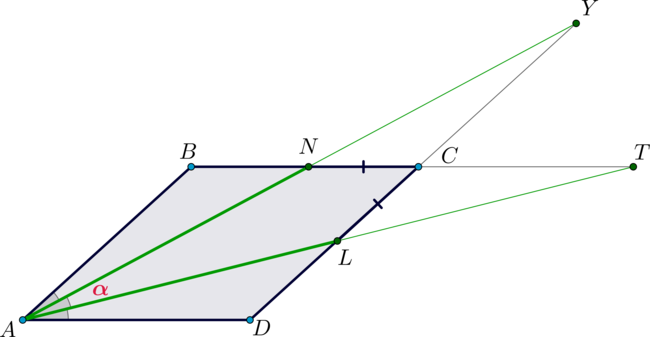
Пусть – точка пересечения прямых
и
, а
– прямых
и
. Пусть
.
как накрест лежащие при
и секущей
. Также
как накрест лежащие при
и секущей
. Заметим, что
как
вертикальные. Следовательно, в
и
равны два угла, следовательно, равны и третьи
углы. Также у них
, следовательно, по признаку “сторона и два прилежащих угла” эти
треугольники равны. Значит,
и
.
Тогда , так как
и прилежащие углы равны (
по
доказанному,
). Отсюда
.
Тогда по этому же признаку (
,
как
противоположные углы параллелограмма
). Значит,
.
Следовательно,
– ромб. Отсюда
.
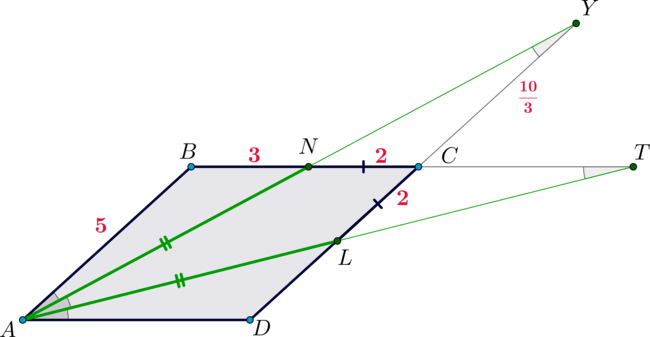
Заметим, что по двум углам, следовательно,
Ошибка.
Попробуйте повторить позже
В прямоугольный треугольник с прямым углом
и катетами
и
вписана
прямоугольная трапеция
так, что
, точки
и
лежат на катетах
и
соответственно, а меньшее основание параллельно гипотенузе. Найдите площадь трапеции.

Рассмотрим рисунок. Заметим, что из условия следует, что основаниями трапеции будут и
. Если меньшее основание трапеции параллельно гипотенузе, то и большее ей параллельно,
следовательно, и
, и
. Так как
и
имеют общую точку
, то
лежит на
. Следовательно, отсюда однозначно определятся, как трапеция вписана в
треугольник.
По теореме Пифагора гипотенуза . Заметим, что
как соответственные
при
и
секущей. Значит, прямоугольные треугольники
и
равны по
катету и острому углу. Следовательно,
. Введем обозначения:
,
,
.
Проведем
.
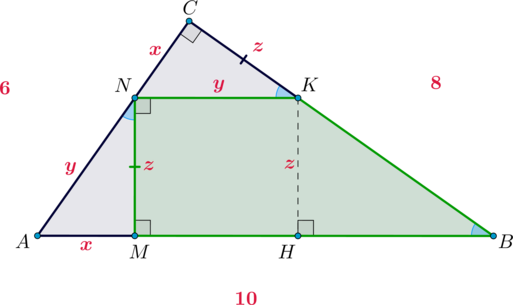
Тогда . Так как
(так как
прямоугольник), то
.
Следовательно,
. Также
. Следовательно, по теореме
Пифагора из
:



