Вписанная и вневписанная окружности
Ошибка.
Попробуйте повторить позже
Дан треугольник , в который вписана окружность с центром
. Пусть
и
— точки касания вписанной окружности со
сторонами
и
. Известно, что
Найдите
Источники:
Пусть Обозначим через точку
пересечение
и
. Тогда, если радиус окружности равен
, то из прямоугольного
треугольника
![]()
Выразим из прямоугольного треугольника
Подставляя в , получаем
как угол треугольника.
Ошибка.
Попробуйте повторить позже
Вписанная окружность треугольника с центром в точке
касается сторон
соответственно в точках
. Точки
и
симметричны вершине
относительно прямых
и
соответственно. Окружности,
построенные на отрезках
и
как на диаметрах, вторично пересекаются в точке
. Докажите, что
лежит на прямой
.
Источники:
Докажем, что точка является серединой отрезка
. Действительно, окружности построены на
и
как на диаметрах,
поэтому
Следовательно, постольку и
— высота равнобедренного треугольника
точка
является серединой его
основания.
![]()
Теперь достаточно проверить, что четырехугольник является параллелограммом. Это так, поскольку
где первое и третье равенство следует из симметрии, а второе верно, поскольку и
являются отрезками касательных,
проведенных из одной точки.
Осталось показать, что Для этого достаточно доказать, что
тогда аналогично
откуда следует требуемое.
Последнее верно, ведь
где обозначает угол между
и
(с другими аналогично).
Ошибка.
Попробуйте повторить позже
Вписанная окружность прямоугольного треугольника
касается окружности, проходящей через середины его
сторон, в точке
Из середины
гипотенузы
проведена касательная
к
отличная от
Докажите, что
.
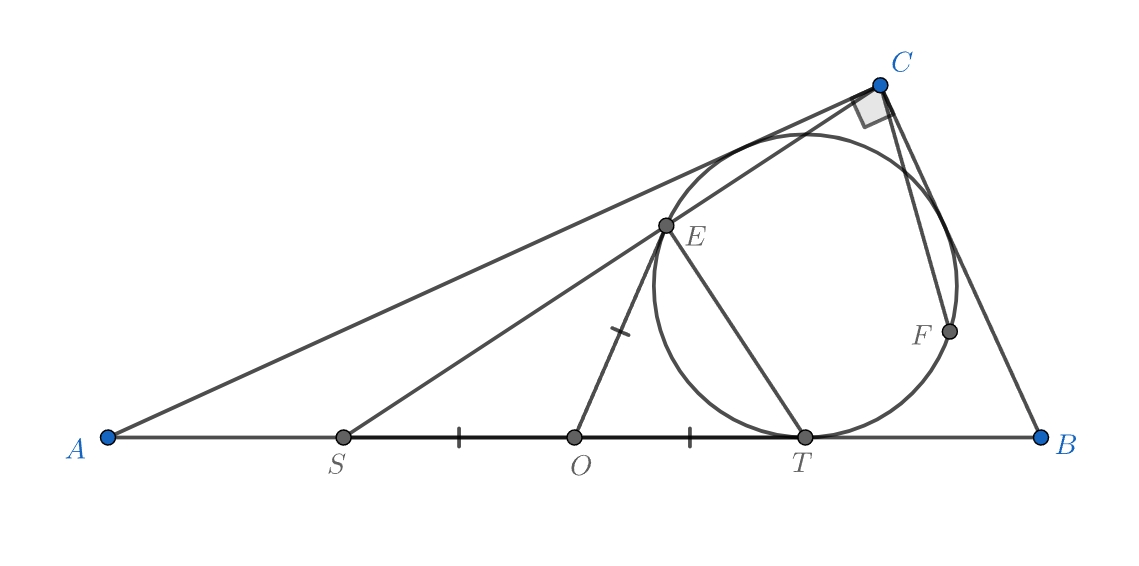
При гомотетии с центром и коэффициентом 2 точка
перейдет в точку касания описанной и полувписанной окружностей
треугольника. Поэтому прямая
симметрична относительно биссектрисы угла
прямой, проходящей через точку касания гипотенузы
с вневписанной окружностью. Пусть вписанная и вневписанная окружности касаются гипотенузы в точках
и
соответственно. Так как
, получаем, что
, т.е. прямая
проходит через точку
диаметрально противоположную
. Но прямая
также проходит через эту точку, следовательно,
лежит на
и симметрична
относительно биссектрисы угла
Ошибка.
Попробуйте повторить позже
Cторона неравнобедренного треугольника
касается вписанной окружности
точке
а вневписанной окружности
в
точке
— диаметр
Пусть
— вторая точка пересечения окружности
прямой
Докажите, что касательная к
в точке
делит сторону
пополам.
Поскольку — диаметр
то
т.е. треугольник
прямоугольный. Пусть
— пересечение касательной к
в точке
с
.png)
Тогда
Получается, что — равнобедренный.
Но если — такая точка на гипотенузе
треугольника
что
то
— середина гипотенузы
.
По свойству вписанной и вневписанной окружности (называемому изотомическим сопряжением точек касания вписанной и вневписанной
окружностей с соответствующей стороной) поэтому
— ещё и середина стороны
Ошибка.
Попробуйте повторить позже
Cторона треугольника
касается вписанной окружности
точке
а вневписанной окружности
в точке
—
середина стороны
— диаметр
Пусть прямая
где
центр вписанной окружности, пересекает высоту
в точке
Докажите, что длина
равна радиусу окружности
Как известно, и
лежат на одной прямой. Тогда рассмотрим треугольник
В нем
— средняя линия (
как
радиусы,
Значит,
Тогда
— параллелограмм (
Поэтому
.png)
Ошибка.
Попробуйте повторить позже
Cторона треугольника
касается вписанной окружности
с центром
точке
— медиана треугольника. Пусть
— точка пересечения медиан треугольника
а
— центр вписанной окружности. Найдите, в каком отношении отрезок
делится
прямой
Пусть
и
Как известно, отрезок
равен радиусу вписанной окружности, то есть
следовательно, четырехугольник
является параллелограмом, откуда
Запишем теорему Менелая для
треугольника
и прямой
Подставляя найденные отношения, получим
следовательно,
.png)
Ошибка.
Попробуйте повторить позже
Определение. Антисерединным треугольником для треугольника называется треугольник, в котором
является серединным
треугольником.
(a) На сторонах и
параллелограмма
выбраны точки
и
соответственно так, что
Докажите, что
точка пересечения отрезков
и
лежит на биссектрисе угла
(b) Используя пункт (a), докажите, что точка Нагеля существует и является центром вписанной окружности антисерединного
треугольника для треугольника
(c) Используя первые два пункта, получите другое доказательство существования прямой Нагеля.
(a) Пусть По теореме Чевы для треугольника
и точки
Воспользуемся подобиями:
и
Получаем, что точка делит сторону
в отношении сторон
и
Значит,
— биссектриса треугольника
.png)
(b) Если в предыдущем пункте предположить, что и
нагелианы треугольника
(условие, что
сохраняется из свойств вневписанных окружностей), то
— точка Нагеля
а
— биссектриса антисерединного треугольника.
Тогда задача сводится к решению пункта (a) для трех возможных параллелограммов, построенных на двух сторонах треугольника
.png)
(c) Рассмотрим гомотетию, переводящую треугольник в его антисерединный треугольник. Центр этой гомотетии,
очевидно, будет в точке пересечения медиан треугольника
При этой гомотетии инцентр
перейдет в инцентр
антисерединного треугольника. Но по предыдущему пункту мы знаем, что инцентр антисерединного треугольника — точка
Нагеля
Тогда и получается, что точка Нагеля, инцентр треугольника и точка пересечения медиан лежат на одной
прямой.
Ошибка.
Попробуйте повторить позже
Прямые и
— касательные в точках
и
к окружности с центром в точке
Через произвольную точку
меньшей дуги
проведена касательная, пересекающая отрезки
и
в точках
и
соответственно. Докажите, что периметр треугольника
и величина угла
не зависят от выбора точки
Заметим, что отрезки касательных к окружности из точки равны, то есть
аналогично
Тогда периметр
равен
величина не зависящая от выбора точки
.png)
Углы и
внешние в
тогда
— центр вневписанной окружности
треугольника
тогда
и
соответственно являются биссектрисами углов
и
величина не зависит от выбора
Ошибка.
Попробуйте повторить позже
(a) Окружности, вписанные в треугольники и
могут касаться только в случае, если касаются их общей касательной
в
одной точке. Обозначим точки касания окружностей, вписанных в
и
за
и
тогда критерий касания
окружностей это равенство отрезков
то есть равенство
то есть
которое справедливо для единственной точки на отрезке
— точки касания вписанной окружности
.png)
(b) Формулировка:
Пусть — точка на продолжении стороны
треугольника
Окружности, вписанные в треугольники
и
касаются тогда и только тогда, когда
совпадает с точкой касания вневписанной окружности треугольника
со стороной
Доказательство:
Скажем лежит на продолжении стороны
за точку
(случаи симметричны). Окружности, вписанные в треугольники
и
могут касаться только в случае, если касаются их общей касательной
в одной точке. Обозначим точки касания
окружностей, вписанных в
и
за
и
тогда критерий касания окружностей это равенство отрезков
то есть равенство
то есть
которое
справедливо для единственной точки на продолжении отрезка
за точку
— точки касания вневписанной окружности
Ошибка.
Попробуйте повторить позже
На окружности зафиксированы точки
и
а точка
скользит по
Найдите геометрическое место точек
служащих для
треугольника
центром одной из вневписанных окружностей.
Рассмотрим такое расположение точек, где точка лежит на большей дуге
Тогда получится треугольник
для которого мы
должны найти геометрическое место точек где будет лежать центр вневписанной окружности. Сначала рассмотрим вневписанную
окружность противоположную углу
Так как центр вневписанной окружности лежит на биссектрисе противоположного ей
угла, то проведем биссектрису
Согласно лемме о трезубце
где
— точка пересечения биссектрис.
![]()
Так как то точка
— фиксированная и не зависит от положения точки
Тогда центр вневписанной окружности (
)
будет лежать на большей дуге
ограниченной прямыми
и
окружности с центром в точке
и радиусом
![]()
Аналогично со случаем, где точка лежит на меньшей дуге
![]()
Теперь рассмотрим случаи вневписанных окружностей, противоположных углам и
Аналогично со случаем вневписанной
окружности, противоположной углу
воспользуемся леммой о трезубце и найдем положения центров. Как следствие из внешней леммы о
трезубце,
и
лежат на одной окружности с центром в точке
Заметим что
значит т.
лежит на середине большей
дуги
и окружность совпадает с окружностью из случая с т.
![]()
Аналогично находим геометрическое место точек для случая, когда т. лежит на меньшей дуге
И получаем ответ:
![]()
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность
радиуса
которая касается стороны
в точке
На окружности отмечена точка
диаметрально противоположная точке
Прямая
пересекает сторону
в точке
причём
Найдите площадь
треугольника
Источники:
Проведём через точку касательную к
пересекающую отрезки
и
в точках
и
соответственно. Пусть
и
—
точки, в которых
касается сторон
и
соответственно.
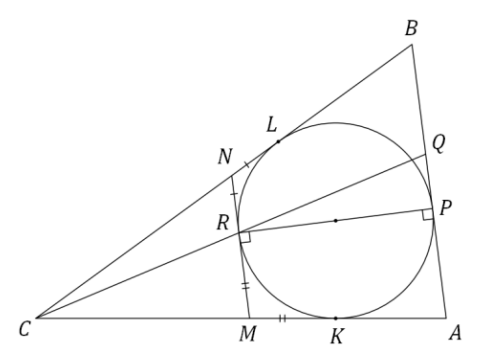
Заметим, что Прямые
и
параллельны как перпендикуляры к
одному диаметру. Поэтому треугольники
и
а также
и
подобны с коэффициентом
Тогда
откуда
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность с центром
которая касается стороны
в точке
Обозначим через
точку касания
вневписанной окружности, лежащей напротив точки
с прямой
Докажите, что отрезок
делит высоту треугольника,
проведённую из вершины
пополам.
Воспользуемся фактом, что на прямой лежит диаметрально противоположная точке
точка
А треугольники
и
гомотететичны (подобны) с центром в точке
![]()
При этой гомотетии медиана треугольника
перейдёт вдоль той же прямой в медиану треугольника
Значит,
делит высоту
пополам.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
Заключительную часть решения можно было обосновать с использованием замечательного свойства трапеции: для
середины оснований и точка
пересечения боковых сторон лежат на одной прямой, поэтому
проходит через середину
Ошибка.
Попробуйте повторить позже
В треугольнике обозначим середины сторон
и
через
и
соответственно. Пусть
— центр вписанной
окружности треугольника
Докажите, что прямая
делит периметр треугольника
пополам.
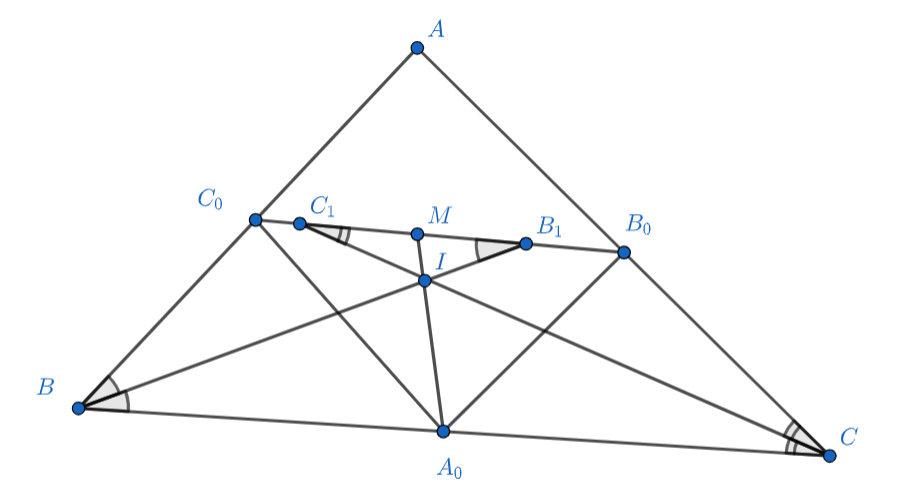
Первое решение.
Пусть и при этом
Пересечём биссектрисы
и
с
в точках
и
соответственно. Тогда в силу параллельности равны отмеченные углы и
Отсюда
следует, что обе точки лежат на отрезке
Кроме того,
и
тогда
Пусть
тогда
в силу подобия
Осталось заметить, что
что и требовалось. Другие соотношения длин сторон рассматриваются аналогично,
поменяется только порядок точек на прямой
Второе решение.
Ясно, что исходный треугольник можно перевести гомотетий в серединный треугольник
Центром этой
гомотетии (неподвижной точкой) является точка пересечения медиан
треугольника
ведь медианы серединного
треугольника пересекаются тоже в точке
Коэффициент этой гомотетии равен
то есть сначала надо стороны
треугольника уменьшить в два раза, а потом сделать центральную симметрию относительно
Куда перейдёт точка
при этой гомотетии? С одной стороны, в центр вписанной в серединный треугольник окружности. С другой стороны, по
определению это будет такая точка
на прямой
, что
Получаем, что на прямой Нагеля
для
серединного треугольника нашлась такая точка
что
Значит, для серединного треугольника точка
является
точкой Нагеля, а прямая
— нагелианой. Известно, что нагелиана делит периметр треугольника пополам, потому
что отрезок касательной к вневписанной окружности как раз равен разности полупериметра треугольника и прилежащей
стороны.
Ошибка.
Попробуйте повторить позже
Пусть — середины сторон треугольника
— центр вписанной в него окружности.
— точка пересечения
прямых
и
— точка пересечения прямых
и
Докажите, что прямая
перпендикулярна прямой
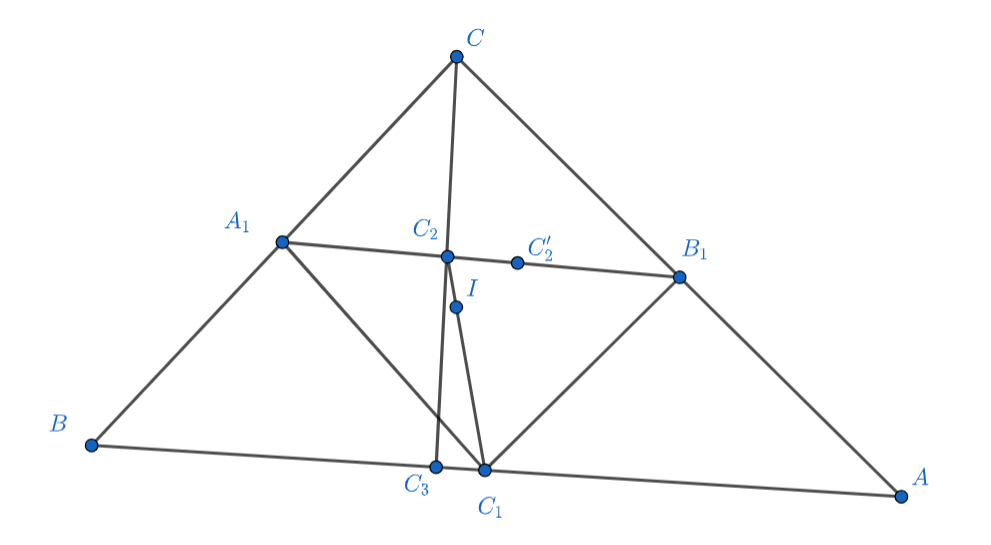
Ясно, что треугольник можно перевести гомотетий в серединный треугольник
Центром этой гомотетии (неподвижной
точкой) является точка пересечения медиан
треугольника
ведь медианы серединного треугольника пересекаются тоже в точке
Коэффициент этой гомотетии равен
то есть сначала надо стороны треугольника уменьшить в два раза, а потом сделать
центральную симметрию относительно
Куда перейдёт точка
при этой гомотетии? С одной стороны, в центр вписанной в серединный
треугольник окружности. С другой стороны, по определению это будет такая точка
на прямой
что
Получаем, что
на прямой Нагеля
для серединного треугольника нашлась такая точка
что
Значит, для серединного треугольника
точка
является точкой Нагеля, а прямая
— нагелианой. То есть
является точкой касания вневписанной окружности
треугольника
Так как в треугольнике точки касания вписанной и вневписанной окружности изотомически сопряжены, то при центральной симметрии
(гомотетии с коэффициентом ) относительно середины
точка
перейдёт в точку
касания вписанной в треугольник
окружности. Значит, тогда
является точкой касания вписанной окружности уже для треугольника
(при симметрии
точка
переходит в точку
).
Осталось рассмотреть гомотетию с центром в точке и коэффициентом
—
переходит в
откуда
будет являться точкой касания вписанной окружности
то есть
как радиус, проведённый в точку
касания.
Ошибка.
Попробуйте повторить позже
Пусть дан треугольник вписанная окружность
с центром в
которого касается сторон
и
в точках
и
Обозначим через
середину стороны
Обозначим через
точку касания вневписанной окружности, лежащей напротив
точки
с прямой
Введём точку
вторую точку пересечения отрезка
со вписанной окружностью, считая от точки
Докажите, что
касается вписанной окружности.
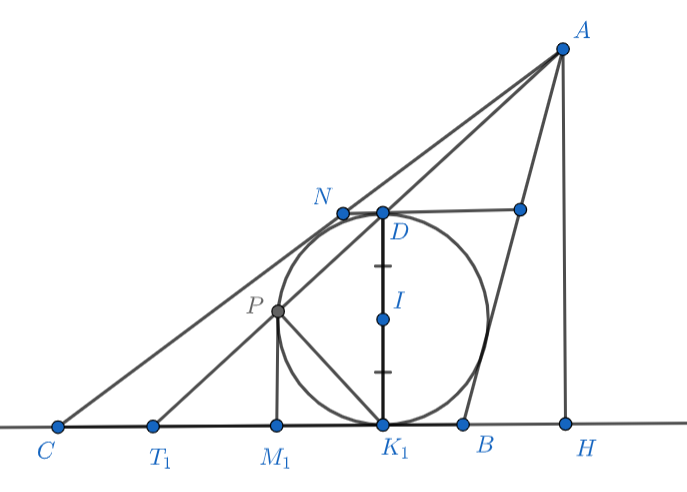
Поскольку — диаметр вписанной окружности, то
Кроме того, нам известно,
что
то есть
— медиана прямоугольного треугольника и
поскольку
— касательная. Заметим, что если провести в точке
касательную, то
она будет образовывать тот же угол с отрезком
откуда
с ней совпадает, что и требовалось.
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике проведена высота
точка
— середина стороны
точка
— центр вневписанной
окружности, касающейся стороны
Прямые
и
пересекаются в точке
Докажите, что отрезок
равен радиусу этой
вневписанной окружности.
![]()
Пусть и
– точки касания прямой
соответственно с вписанной и вневписанной окружностями. Элементарно выводится, что
. Сделаем гомотетию с центром в точке
и коэффициентом, равным отношению радиусов
вписанной и вневписанной окружностей, при которой
перейдёт в
. Тогда точка
касания вневписанной окружности отрезка
(эта окружность стала вписанной для
) естественно лежит на прямой
, соединяющей центр гомотетии с прообразом
точки
. Отсюда
и
(радиус вневписанной окружности), тогда
, как средняя линия в
.
При этом
, потому что обе эти прямые перпендикулярны
. Значит,
— параллелограмм по определению, поэтому
.
Ошибка.
Попробуйте повторить позже
Пусть и
— середины гипотенузы
и катета
прямоугольного треугольника
соответственно. Вневписанная окружность
треугольника
касается стороны
в точке
, а прямой
в точке
Докажите, что точки
и
лежат на одной
прямой.
Пусть — центр вневписанной окружности треугольника
, тогда
и
— проекции точки
на прямые
и
соответственно:
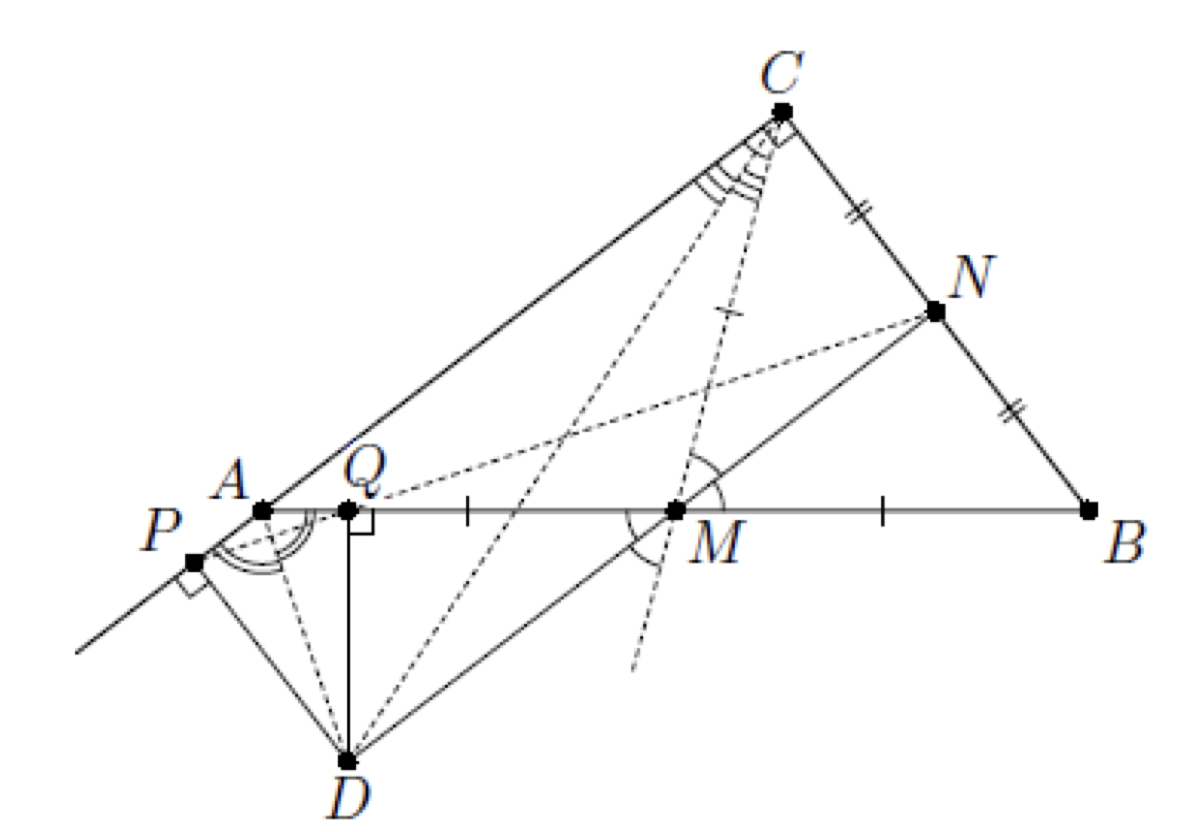
Так как — медиана равнобедренного треугольника
, проведённая к основанию, то
— биссектриса угла
, поэтому
точка
лежит на прямой
Кроме того,
средняя линия треугольника
, значит,
Таким образом,
—
прямоугольник.
Пусть , тогда
, а
биссектриса угла
Следовательно,
, поэтому
Поскольку точка
симметрична точке
относительно прямой
, то
лежит на
Ошибка.
Попробуйте повторить позже
На сторонах и
квадрата
выбраны точки
и
таким образом, что угол
равен
Длина стороны квадрата
равна 1. Найдите периметр треугольника
Источники:
Первое решение.
Вспомним, что угол, под которым видна сторона треугольника из центра вневписанной окружности, равен где
— угол, в
который окружность вневписана.
Центр вневписанной окружности треугольника лежит на прямой
т.к. биссектриса совпадает с диагональю квадрата
Но
при этом
то есть точка как раз является центром вневписанной окружности треугольника
![]()
Тогда точки и
— точки касания вневписанной окружности с продолжениями сторон треугольника
а его периметр равен
Второе решение.
Если отразить точку относительно прямой
а затем относительно прямой
то она перейдет в точку
Действительно
композиция двух осевых симметрий относительно пересекающихся прямых — это поворот на удвоенный угол между прямыми. То есть в
нашем случае эти две симметрии эквивалентны повороту на угол
относительно точки
Это означает, что образ точки
при
симметрии относительно
и образ точки
при симметрии относительно
— это одна и та же точка; на рисунке она обозначена
![]()
Из точки отрезки
и
видны под углом
(при симметрии сохраняются величины углов, поэтому например, углы
и
равны). Значит, точка
— это основание перпендикуляра, опущенного из точки
на прямую
И, наконец, поскольку
и
(при симметрии длины отрезков сохраняются), видим, что периметр треугольника
равен сумме длин сторон
и
квадрата.
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность, которая касается стороны
в точке
. Могут ли оба центра окружностей, одна из которых
вписана в треугольник
, вторая — в треугольник
, одновременно лежать на окружности, вписанной в треугольник
?
Ответ объясните.
Источники:
Предположим, что центры и
лежат на окружности, вписанной в треугольник
. Тогда
— биссектрисы
соответствующих углов
точки
и
лежат на
и
.
![]()
Далее имеем
— диаметр
точка
точки
лежат на одной прямой
противоречие!
Ошибка.
Попробуйте повторить позже
Дан описанный четырехугольник у которого радиусы вписанных окружностей треугольников
и
равны. Найдите угол
между диагоналями
и
Докажем, что точки касания вписанных окружностей треугольников и
с диагональю
совпадают.
![]()
В самом деле, обозначим точки касания и
соответственно. Тогда
Критерий описанности четырехугольника
что равносильно равенству
Теперь легко видеть, что картинка однозначно задается радиусом вписанных окружностей треугольников и
и
расстояниями от точки касания до точек
и
Значит, картинка переходит в себя при симметрии относительно прямой
при этом
точки
и
меняются местами. Но это означает, что
перпендикулярна



