№14 из ЕГЭ 2019
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дана пирамида в которой
а) Докажите, что ребро перпендикулярно ребру
б) Найдите расстояние между ребрами и
Источники:
а) Пусть — середина
тогда
— медиана и высота в равнобедренном треугольнике
— медиана и высота
в равнобедренном треугольнике
![]()
Тогда и
следовательно,
Так как
лежит в
то
б) Треугольники и
равны по трем сторонам, так как
— общая,
следовательно, их
медианы тоже равны:
![]()
Проведем медиану в равнобедренном треугольнике
Отрезок
перпендикулярен прямой
так как лежит
в плоскости
и по пункту а)
Кроме того, отрезок
перпендикулярен
так как медиана к
основанию в равнобедренном треугольнике является высотой. Получили, что
перпендикулярен
и
следовательно,
его длина равна расстоянию между
и
Осталось найти длину По теореме Пифагора для треугольника
По теореме Пифагора для треугольника
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде точка
делит сторону
в отношении
считая от вершины
Точка
делит сторону
в отношении
считая от вершины
Через точки
и
параллельно ребру
проведена
плоскость
а) Докажите, что сечение пирамиды плоскостью является прямоугольником.
б) Найдите расстояние от точки до плоскости
если известно, что
Источники:
а) Пусть заданная в условии плоскость пересекает и
в точках
и
соответственно. Тогда
Из параллельности следует, что с коэффициентом
а также
с
коэффициентом
Из подобия имеем
причем по условию
Получили, что равен и параллелен
значит,
— параллелограмм. Осталось доказать, что
из
этого будет следовать, что
является прямоугольником.
![]()
Пусть — проекция точки
на плоскость
тогда
— центр равностороннего треугольника
а значит,
прямая
— биссектриса, медиана и высота, так как пирамида правильная. Точка
— пересечение прямых
и
Тогда по обратной теореме Фалеса
Кроме того, с привлечением теоремы о трех перпендикулярах имеем:
Тогда получаем
Вспомним, что тогда
значит,
— прямоугольник.
б) значит, расстояние от
до
равно расстоянию от прямой
до плоскости
Пусть — основание перпендикуляра из
на
— точка пересечения
и
В пункте а) мы уже показали, что плоскость перпендикулярна прямым
и
а значит и всей плоскости
Точка также лежит в плоскости
получаем, что часть отрезка
заключенная между отрезками
и
и есть искомое расстояние.
![]()
Найдем отрезок — высоту в равностороннем треугольнике
По теореме Пифагора для
Пусть тогда по теореме Пифагора для
При этом тогда по теореме Пифагора для
Приравняем
Тогда
Треугольники и
подобны с коэффициентом
поэтому нужная нам часть отрезка
равна
![]()
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В конусе с вершиной и центром основания
радиус основания равен 13, а высота равна
Точки
и
— концы
образуюших,
— середина
— точка в плоскости основания такая, что прямая
параллельна прямой
a) Докажите что — прямой угол.
6) Найдите угол между и плоскостью основания, если
Источники:
а) Обозначим через середину отрезка
и покажем, что на самом деле это та самая точка
из условия
задачи. Отрезок
как средняя линия в треугольнике
При этом мы знаем, что через
можно
единственным способом провести прямую, параллельную
значит,
и является этой самой прямой.
![]()
Рассмотрим треугольник Он равнобедренный, поскольку
как радиусы основания конуса. Точка
—
середина
тогда
является медианой, а значит и высотой в равнобедренном треугольнике
Получили
что и требовалось доказать.
б) Угол между прямой и плоскостью есть угол между этой прямой и ее проекцией эту плоскость. Отрезок
перпендикулярен плоскости основания, следовательно,
является проекцией
на плоскость основания. Тогда проекцией
середины
отрезка
будет середина
отрезка
Получили, что
является проекцией
на плоскость
основания и искомый угол равен углу
![]()
Отрезок является средней линией в треугольнике
тогда имеем:
Найдем по формуле для медианы через стороны треугольника
Тогда из прямоугольного треугольника
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильном тетраэдре точки
и
— середины рёбер
и
соответственно. Плоскость
содержит прямую
и параллельна прямой
.
а) Докажите, что сечение тетраэдра плоскостью — квадрат.
б) Найдите площадь сечения тетраэдра плоскостью
, если
.
Источники:
а) Пусть точки ,
— середины ребер
и
соответственно. Тогда
— средняя линия треугольника
, значит,
. Аналогично
, следовательно
.
Значит, точки ,
,
,
лежат в одной плоскости, которая параллельна прямой
, следовательно, это и
есть плоскость
.
Так как тетраэдр правильный, его грани — это равные правильные треугольники. Тогда их средние линии попарно
равны, в частности, , значит,
— ромб.
Рассмотрим треугольники и
. В них
и
, так как тетраэдр
правильный. Тогда
по третьему признаку равенства треугольников. В равных треугольниках
соответственные элементы равны, значит, равны и их медианы, то есть
. Следовательно,
—
квадрат.
![]()
б) Площадь квадрата равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В кубе рёбра равны 1. На продолжении отрезка
за точку
отмечена точка
так, что
а на продолжении отрезка
за точку
отмечена точка
так, что
a) Докажите, что
б) Найдите расстояние между прямыми и
Источники:
а) Рассмотрим треугольник . В нем
,
и
. Тогда по теореме
косинусов:
Отсюда
Рассмотрим треугольник . В нем
,
и
. Тогда по теореме
косинусов:
Рассмотрим треугольник . В нем
,
и
. Тогда по теореме
косинусов:
Отсюда
![]()
б) Заметим, что . Тогда проекцией прямой
на плоскость
является точка
.
Найдем проекцию на плоскость
. Пусть точка
— такая точка на продолжении отрезка
за точку
, что
. Тогда
— проекция точки
на
, так как
— параллелограмм и
.
Пусть точка — такая точка на продолжении отрезка
за точку
, что
. Тогда
— проекция точки
на
, так как
— параллелограмм и
.
![]()
Тогда по построению прямая параллельна плоскости
и искомое расстояние равно расстоянию между
этими прямой и плоскостью. При этом перпендикуляр из точки
к прямой
по построению перпендикулярен двум
прямым плоскости
.
Тогда расстояние между прямыми и
равно расстоянию между точкой
и прямой
.
Рассмотрим треугольник . В нем
,
и
. Значит, по теореме
Пифагора
. Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна
. Значит, расстояние между прямыми
и
равно
.
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна 9, а боковое ребро
На рёбрах
и
отмечены точки
и
соответственно, причём
Плоскость
содержит прямую
и
параллельна прямой
a) Докажите, что плоскость делит ребро
в отношении
считая от вершины
б) Найдите расстояние между прямыми и
Источники:
а) Пусть плоскость пересекает ребро
в точке
По условию
значит, она пересекает грань
по прямой,
параллельной
следовательно,
Тогда по теореме о пропорциональных отрезках точка
делит ребро
в
отношении
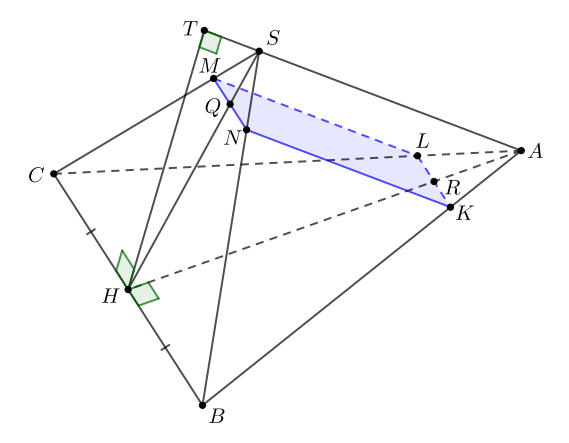
б) Пусть плоскость пересекает ребро
в точке
Аналогично предыдущему пункту получим, что
Тогда
значит, по теореме, обратной теореме о пропорциональных отрезках,
Пусть — середина стороны
Тогда
— высота, медиана и биссектриса равностороннего треугольника
Пусть
— точка пересечения
и
По теореме о пропорциональных отрезках
Пусть — точка пересечения
и плоскости
Так как
то плоскость
пересекает плоскость
по
прямой, параллельной
то есть
Тогда
Заметим, что так как прямая то искомое расстояние от прямой
до прямой
равно расстоянию между
параллельными прямыми
и
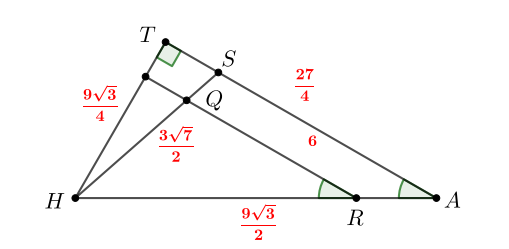
Рассмотрим треугольник пусть
— его высота. Тогда прямая
делящая стороны
и
в
отношении
считая от вершины
делит высоту
в том же отношении. Значит, расстояние между прямыми
и
равно
Найдем длины сторон треугольника По условию
Отрезок
— высота равностороннего треугольника
со стороной 9, значит,
Отрезок
— медиана равнобедренного треугольника
значит, и высота. По
теореме Пифагора для треугольника
Запишем теорему косинусов для треугольника
Подставив значения сторон, найдем

Рассмотрим треугольник В нем
поэтому
Следовательно,
Тогда расстояние между прямыми и
равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде точка
делит сторону
в отношении
считая от вершины
точка
делит сторону
в отношении
считая от вершины
Через точки
и
параллельно прямой
проведена
плоскость
a) Докажите, что сечение пирамиды плоскостью параллельно прямой
б) Найдите расстояние от точки до плоскости
если известно, что
Источники:
а) По условию значит, по теореме о пропорциональных отрезках прямые
и
параллельны. Поскольку прямая
параллельна лежащей в плоскости сечения прямой
она параллельна и самой
плоскости сечения
по признаку параллельности прямой и плоскости.
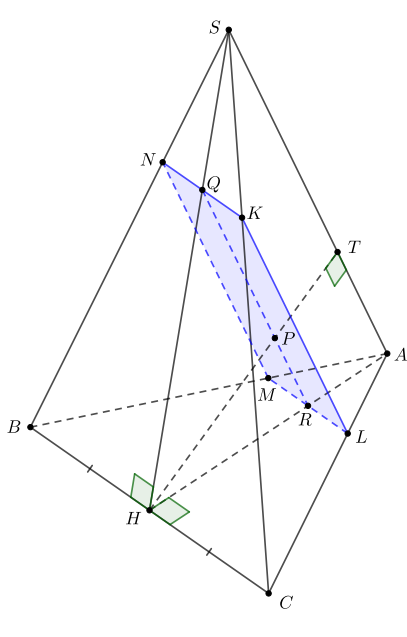
б) Пусть — середина
Проведём
и
и пусть плоскость
пересекает
по прямой
Тогда
и
параллельны, а расстояние от точки
до плоскости
равно расстоянию от точки
до плоскости
Пусть — высота треугольника
тогда отрезок
перпендикулярен ребру
В силу параллельности
и
отрезки
и
также перпендикулярны.
Кроме того, ребро перпендикулярно плоскости
по признаку перпендикулярности прямой и плоскости, а потому
и
перпендикулярно
Но
параллельно
поэтому
и
перпендикулярны.
Тем самым прямая перпендикулярна двум пересекающимся прямым
и
лежащим в плоскости
сечения, а значит, и всей плоскости сечения. Пусть
пересекает
в точке
Тогда
— искомое
расстояние.

Рассмотрим треугольник Найдем длины его сторон. По условию
Отрезок
— высота равностороннего
треугольника
со стороной 6, значит,
Отрезок
— высота равнобедренного треугольника
По
теореме Пифагора для треугольника
Запишем теорему косинусов для треугольника
Подставив значения сторон, найдем
![]()
Рассмотрим треугольник В нем
поэтому
Следовательно,
Заметим, что в треугольнике прямые
и
параллельны и
значит, по теореме, обратной
теореме о пропорциональных отрезках,
следовательно,
Тогда расстояние от точки до плоскости
равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана пирамида в которой
a) Докажите, что ребро перпендикулярно ребру
б) Найдите угол между прямой и плоскостью
Источники:
а) Пусть — середина
тогда
— медиана и высота в равнобедренном треугольнике
— медиана и высота
в равнобедренном треугольнике
![]()
Тогда
Так как лежит в
то
б) Рассмотрим треугольник Проведем в нем высоту
Заметим, что
так как
По
построению
значит,
Следовательно, прямая
является проекцией прямой
на
плоскость
значит, угол между прямой
и плоскостью
равен углу между прямыми
и
Найдем угол треугольника
По условию Найдем стороны
и
Так как
— высота равнобедренного треугольника
то по
теореме Пифагора:
Аналогично — высота равнобедренного треугольника
тогда по теореме Пифагора:
![]()
Запишем теорему косинусов для треугольника
Подставим найденные ранее значения и вычислим косинус угла
Значит, угол между прямой и плоскостью
равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна 6, а боковое ребро
равно 7. На рёбрах
и
отмечены точки
и
соответственно, причём
Плоскость
содержит прямую
и
параллельна прямой
a) Докажите, что плоскость параллельна прямой
б) Найдите угол между плоскостями и
а) Пусть плоскость пересекает ребро
в точке
Прямые
и
параллельны, так как плоскость
параллельна
значит, по теореме о пропорциональных отрезках
![]()
Следовательно, по теореме, обратной теореме о пропорциональных отрезках, Таким образом, плоскость
содержащая прямую
параллельна прямой
б) Пусть — середина ребра
тогда
— медиана и высота в равнобедренном треугольнике
— медиана и высота в равностороннем треугольнике
Тогда
и
следовательно,
Плоскость перпендикулярна плоскости
параллельной прямой
и плоскости
содержащей прямую
Поскольку плоскость
параллельна прямой
лежащей в плоскости
то искомый угол равен углу между
прямой
и плоскостью
Рассмотрим треугольник Проведем в нем высоту
Заметим, что
так как
По
построению
значит,
Следовательно, прямая
является проекцией прямой
на
плоскость
Значит, угол между прямой
и плоскостью
равен углу между прямыми
и
![]()
Найдем угол треугольника
По условию
Найдем стороны
и
Отрезок
— высота
равностороннего треугольника
со стороной, равной 6 по условию, значит,
Отрезок — высота равнобедренного треугольника
тогда по теореме Пифагора
Запишем теорему косинусов для треугольника
Подставим найденные ранее значения и вычислим косинус угла
Значит, угол между плоскостью и плоскостью
равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна 6, а боковое ребро
равно 5. На рёбрах
и
отмечены точки
и
соответственно, причём
Плоскость
содержит прямую
и
параллельна
a) Докажите, что сечение пирамиды плоскостью
— прямоугольник.
б) Найдите объём пирамиды, вершиной которой является точка а основанием — сечение пирамиды
плоскостью
Источники:
а) Пусть плоскость пересекает ребра
и
в точках
и
соответственно, а точка
— середина ребра
. Тогда
— медиана и высота в равнобедренном треугольнике
,
— медиана и высота в
равностороннем треугольнике
. Значит,
и
, следовательно,
.
Прямая, перпендикулярная плоскости, перпендикулярна каждой прямой этой плоскости, значит,
.
![]()
Плоскость , параллельная прямой
, пересекает плоскости
и
по прямым
и
,
значит,
и
. Тогда по теореме о пропорциональных отрезках
Значит, по теореме, обратной теореме о пропорциональных отрезках, прямые и
параллельны прямой
. Таким образом,
является параллелограммом, пары противоположных сторон которого параллельны
перпендикулярным прямым
и
соответственно, то есть
— прямоугольник.
б) Прямая , параллельная прямой
, перпендикулярна плоскости
, значит, плоскости
и
перпендикулярны.
Пусть плоскость пересекает прямые
и
в точках
и
соответственно. Тогда высота
пирамиды
равна расстоянию
между точкой
и прямой
.
Пусть — высота правильной пирамиды
, тогда
лежит в плоскости
и
.
— медиана равностороннего треугольника
со стороной 6, значит,
Найдем косинус и синус угла :
Пусть — перпендикуляр, опущенный из точки
на прямую
. Тогда
![]()
— катет прямоугольного треугольника
. Гипотенуза
треугольника
равна
Тогда можем найти :
Найдем . Так как в треугольнике
,
Найдем . Так как в треугольнике
,
Найдем объем пирамиды :
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде сторона основания
равна 4, а боковое ребро
На рёбрах
и
отмечены точки
и
соответственно, причём
Плоскость
содержит прямую
и
параллельна прямой
a) Докажите, что плоскость делит ребро
в отношении
считая от вершины
б) Найдите расстояние между прямыми и
Источники:
а) Пусть плоскость пересекает ребра
и
в точках
и
соответственно. По условию
значит, она
пересекает плоскость
содержащую прямую
по прямой, параллельной
то есть
Тогда
—
прямоугольник, следовательно,
Четырехугольник — квадрат, то есть
значит,
следовательно,
и
![]()
б) По теореме о пропорциональных отрезках так как
По предыдущему пункту
Тогда плоскости
и
параллельны, так как образованы двумя парами параллельных прямых.
Следовательно, расстояние между скрещивающимися прямыми
и
равно расстоянию между параллельными
плоскостями
и
содержащими их.
Пусть точки и
— середины
и
соответственно. Рассмотрим треугольник
пусть
— его
высота.
Заметим, что — высота и медиана равнобедренного треугольника
значит,
Так как
— средняя
линия квадрата
то
Тогда
Прямая, перпендикулярная плоскости, перпендикулярна каждой прямой этой плоскости, следовательно, По
построению
значит,
Так как
то
![]()
Пусть плоскость пересекает
в точке
, тогда расстояние между
и
равно длине отрезка
Пусть — точка пересечения
и
— точка пересечения
и
Аналогично предыдущему пункту можем получить, что
По условию значит, она пересекает плоскость
содержащую прямую
по прямой, параллельной
то есть
Рассмотрим треугольник В нем
и
значит, по теореме о пропорциональных отрезках
Рассмотрим треугольник В нем
значит, по обратной теореме о пропорциональных
отрезках
Тогда рассмотрим треугольник
и аналогично получим, что
следовательно,
Найдем Отрезок
— высота треугольника
Найдем стороны треугольника
Имеем
Отрезки
и
— высоты равных равнобедренных треугольников
и
Тогда по теореме
Пифагора
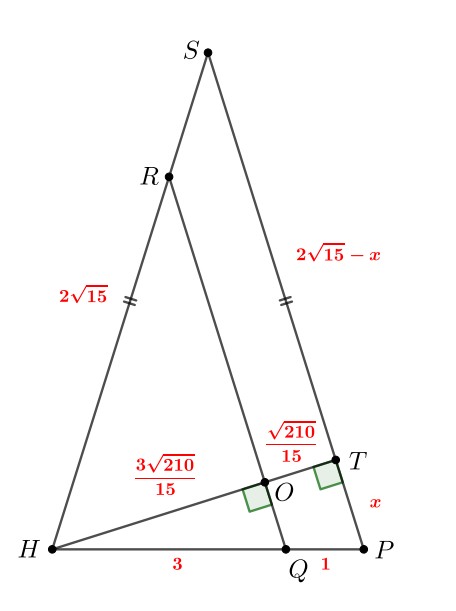
Пусть тогда
По теореме Пифагора для треугольников
и
Тогда имеем уравнение:
Найдем отрезки и
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме сторона основания равна 4, а боковое ребро равно 2. Точка
— середина
ребра
а точка
— точка пересечения диагоналей боковой грани
a) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы плоскостью
лежит на отрезке
б) Найдите угол между прямой и плоскостью
Источники:
а) Плоскость параллельна прямой
значит, плоскость
пересекает
по прямой, параллельной
Пусть
пересекает ребро
в точке
тогда
а значит,
Таким образом,
—
средняя линия треугольника
Рассмотрим сечение Это трапеция, так как
Также
Тогда, если
—
точка пересечения диагоналей трапеции
треугольники
и
подобны с коэффициентом 2.
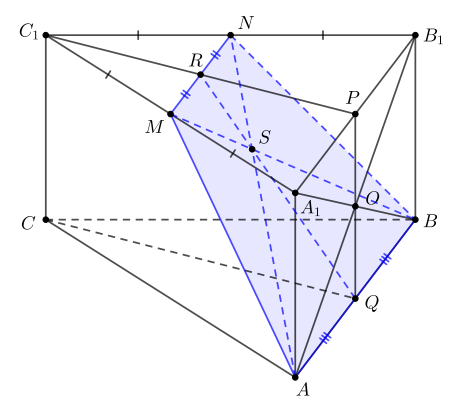
Пусть точки и
— середины
и
соответственно.
— точка пересечения
и
Тогда
—
середина
значит,
— отрезок, соединяющий середины оснований трапеции. Тогда точка пересечения диагоналей
лежит на нем, значит,
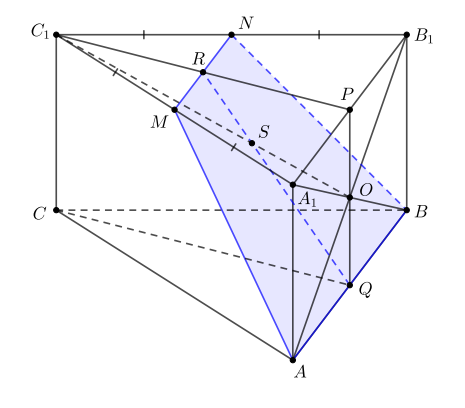
Рассмотрим треугольник в плоскости
Заметим, что
и
— медианы этого треугольника. Пусть
— точка их пересечения. Тогда
![]()
Мы получили, что точки и
делят отрезок
в отношении
значит, они совпадают, то есть точка
лежит на
б) Плоскость сечения образована параллельными прямыми и
так как
и
Тогда
Значит, углов между прямой
и плоскость.
равен углу между прямыми
и
то
есть углу
Найдем стороны треугольника Так как
— медиана равностороннего треугольника
— медиана треугольника
значит,
По теореме Пифагора для треугольника
— медиана треугольника
, значит,
. По теореме Пифагора для треугольника
Запишем теорему косинусов для треугольника
Подставив найденные значения, получаем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



