18.25 Графика. Отрезок, ромб, квадрат и другие нестандартные графики
Ошибка.
Попробуйте повторить позже
Найдите значения параметра , при которых система
имеет ровно три решения.
Красивое решение
Построим на координатной плоскости множество решений уравнения
— квадратик с вершинами в точках
,
,
и
.
![]()
График функции это парабола с вершиной в точке с
координатами
. Заметим, что и квадратик, и парабола симметричны
относительно оси ординат, следовательно, множество точек их пересечения также
симметрично относительно оси ординат. Нам нужно найти такое значение
параметра
, при котором это множество содержит ровно три точки. Три —
нечётное число, значит, хотя бы одна из точек пересечения должна лежать на оси
ординат (ведь если бы не лежало ни одной, то из соображений симметрии точек
было бы четное число).
Квадратик пересекает ось ординат только в двух точках — и
. Парабола
может проходить через них только тогда, когда одна из точек
или
является её вершиной. Значит, достаточно рассмотреть только эти два
случая.
- Если
— вершина параболы, то
Но тогда
. Значит, точка
— единственная точка пересечения параболы и квадратика.
- Если
— вершина параболы, то
. Тогда
. Значит, ветви этой параболы проходят через точки
и
. Больше точек пересечения нет, поэтому парабола
нам подходит.
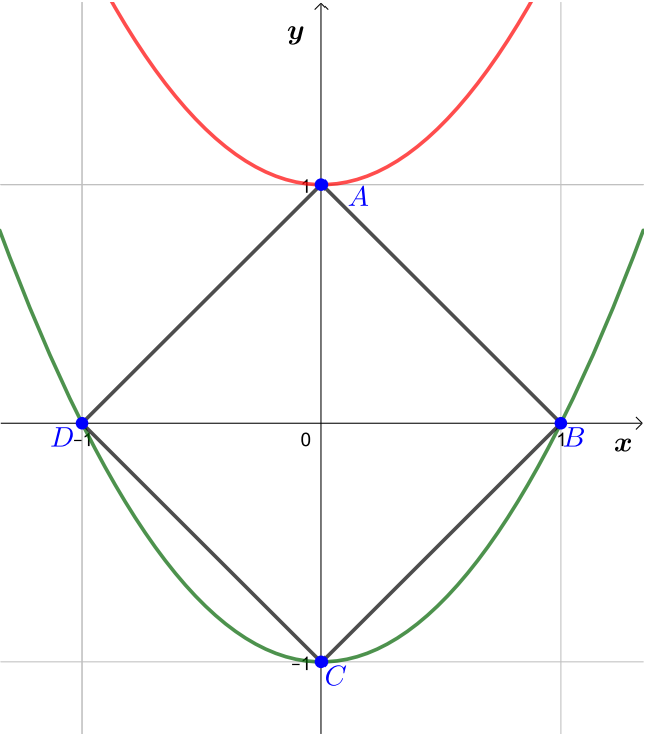
Мы выяснили, что другие параболы будут пересекать квадратик в чётном числе
точек, поэтому ответ — .
Стандартное решение
Построим на координатной плоскости множество решений уравнения
— квадратик с вершинами в точках
,
,
и
.
![]()
Будем анализировать, как выглядит график функции в
зависимости от значения
. Это парабола с вершиной в точке с координатами
. Заметим, что при
график функции
проходит через
точки
,
и
. Тогда при
этот график не пересекает квадратик ни в
одной точке.
![]()
Если мы начнем уменьшать то график начнёт двигаться вверх, пересекая
каждый из отрезков
и
в двух точках, а каждый из отрезков
и
в одной. То есть у нас будет 6 точек пересечения графика
с
квадратиком. Так будет до тех пор, пока график
не достигнет положения
касания с отрезками
и
. В этот момент он будет пересекать
каждый из отрезков
и
в одной точке. То есть у нас будет 4
точки пересечения графика
с квадратиком. После этого момента, до
момента, когда
станет равно
, график
будет пересекать
отрезки
и
ровно по одному разу. В момент
график
будет проходить только через точку
квадратика. При
график
и квадратик пересекаться не будут. Значит, единственное подходящее
.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получено верное значение параметра, но есть недостаток в обосновании | 3 |
| Верно рассмотрены ключевые положения квадрата и параболы, но верное значение параметра либо не найдено, либо получены посторонние значения | 2 |
| Обоснованно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите значения параметра , при которых уравнение
Второе уравнение системы задает окружность с центром в точке и радиусом 1.
Напомним, что расстояние между точками и
на плоскости задается выражением
Рассмотрим первое уравнение системы. Первое слагаемое левой части равно расстоянию между точками и
. Второе слагаемое левой части равно расстоянию между точками
и
. Выражение в правой
части уравнения равно расстоянию между точками
и
.
Получили, что первое уравнение системы равносильно тому, что длина отрезка (правая часть) равна
сумме длин отрезков
и
(левая часть). По неравенству треугольника такое возможно только при
условии, что точка
лежит на отрезке
. Точка
зафиксирована, а точка
может лежать в
любом месте прямой
в зависимости от значения параметра
. Теперь можем нарисовать картинку.
![]()
Отметим ключевое для нас положение точки
на прямой
. В этом положении отрезок касается
окружности, т.е. имеет с ней единственную точку пересечения. Если
будет лежать выше, чем
, то отрезок не
будет иметь общих точек с окружностью. Если же
будет лежать ниже, чем
, то отрезок
будет иметь ровно
две точки пересечения с окружностью. Нас интересует последний случай. Осталось найти координаты точки
.
Обозначим точку через
, точку касания
с окружностью через
, точку
через
.
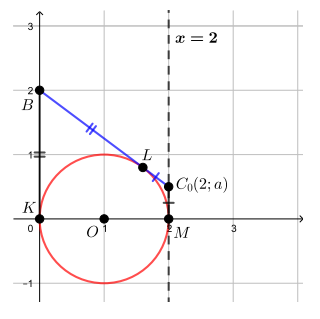
как отрезки касательных к окружности из точки
, и
как отрезки касательных к
окружности из точки
. Тогда
. Выразим длину отрезка
через координаты его
концов, получим уравнение
Так как отрезок имеет два пересечения с окружностью при всех положениях ниже, чем
, нам
подойдут
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет ровно два решения.
Первое уравнение задает окружность с центром в точке (центр движется по прямой
) и радиусом
Рассмотрим второе уравнение. Пусть имеются точки
Тогда второе уравнение имеет вид
, следовательно, задает множество точек
находящихся на отрезке
Заметим, что длина отрезка равна
диаметру окружности. Определим как располагается отрезок относительно траектории движения центра окружности. Для этого
найдем уравнение прямой, на которой лежит отрезок:
Следовательно, отрезок лежит на траектории движения точки Тогда единственное положение, когда окружность имеет с
отрезком две общие точки, следующее:
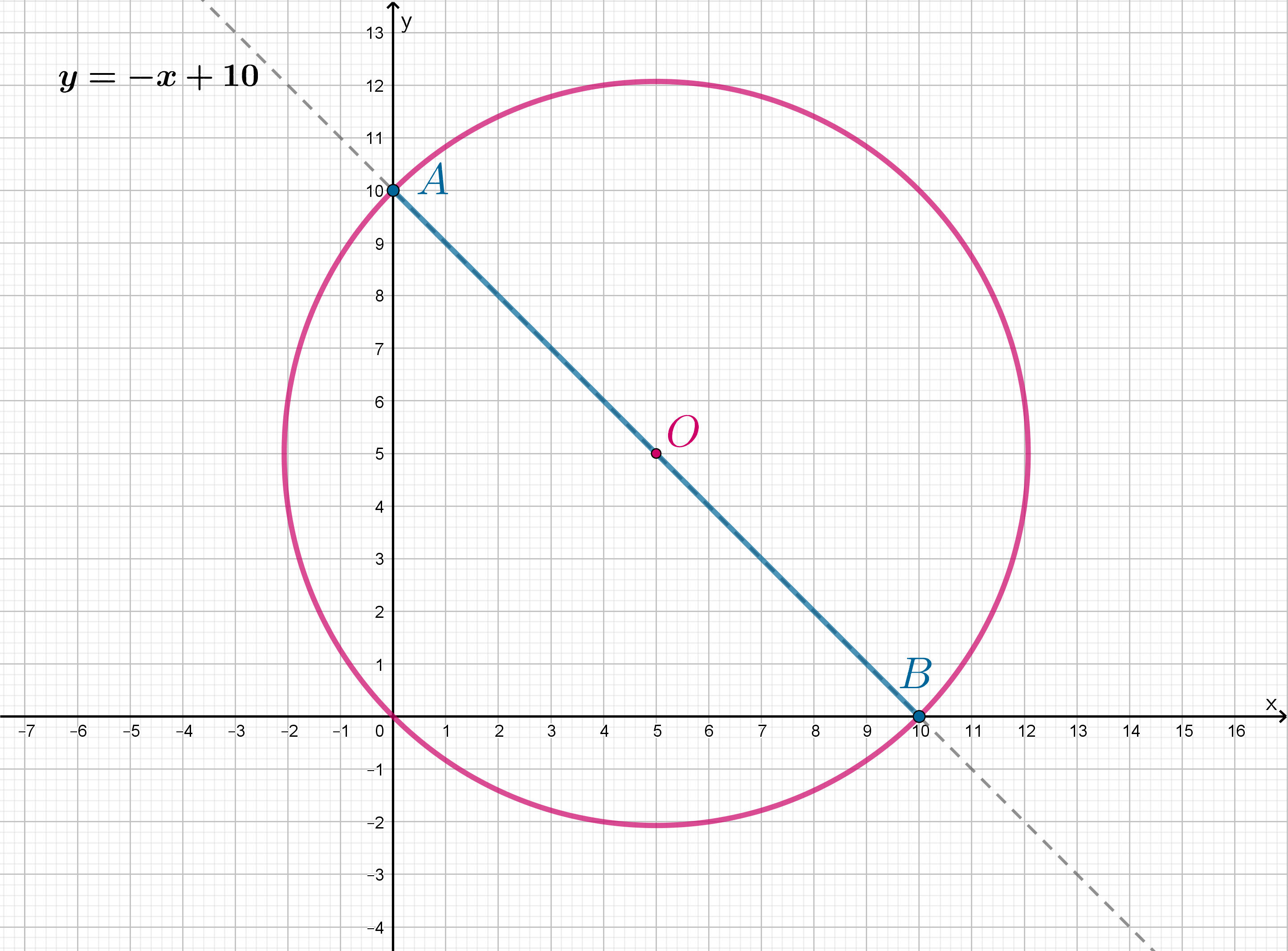
Следовательно, — середина отрезка
значит,
Отсюда
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно получено уравнение, на котором лежит отрезок | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Если , то левая часть первого равенства равна нулю, значит оба подкоренных выражения равны нулю, откуда
–
единственное решение системы.
Если : неравенство задает внутренность круга (вместе с границей) с центром в точке
и
.
Рассмотрим три точки: ,
,
. Тогда первый корень равен длине отрезка
, второй корень – длине отрезка
,
а
. Следовательно, первое уравнение задает множество точек
, лежащих на отрезке
. Заметим, что при
противоположных
картинка симметрична относительно начала координат (при
отрезок находится в 4 четверти, а при
— во
второй), следовательно, если нам подойдет
, то нам также подойдет и
. Далее будем рассматривать
только положительные
. Тогда
лежит на положительной полуоси абсцисс, а
– на отрицательной полуоси ординат.
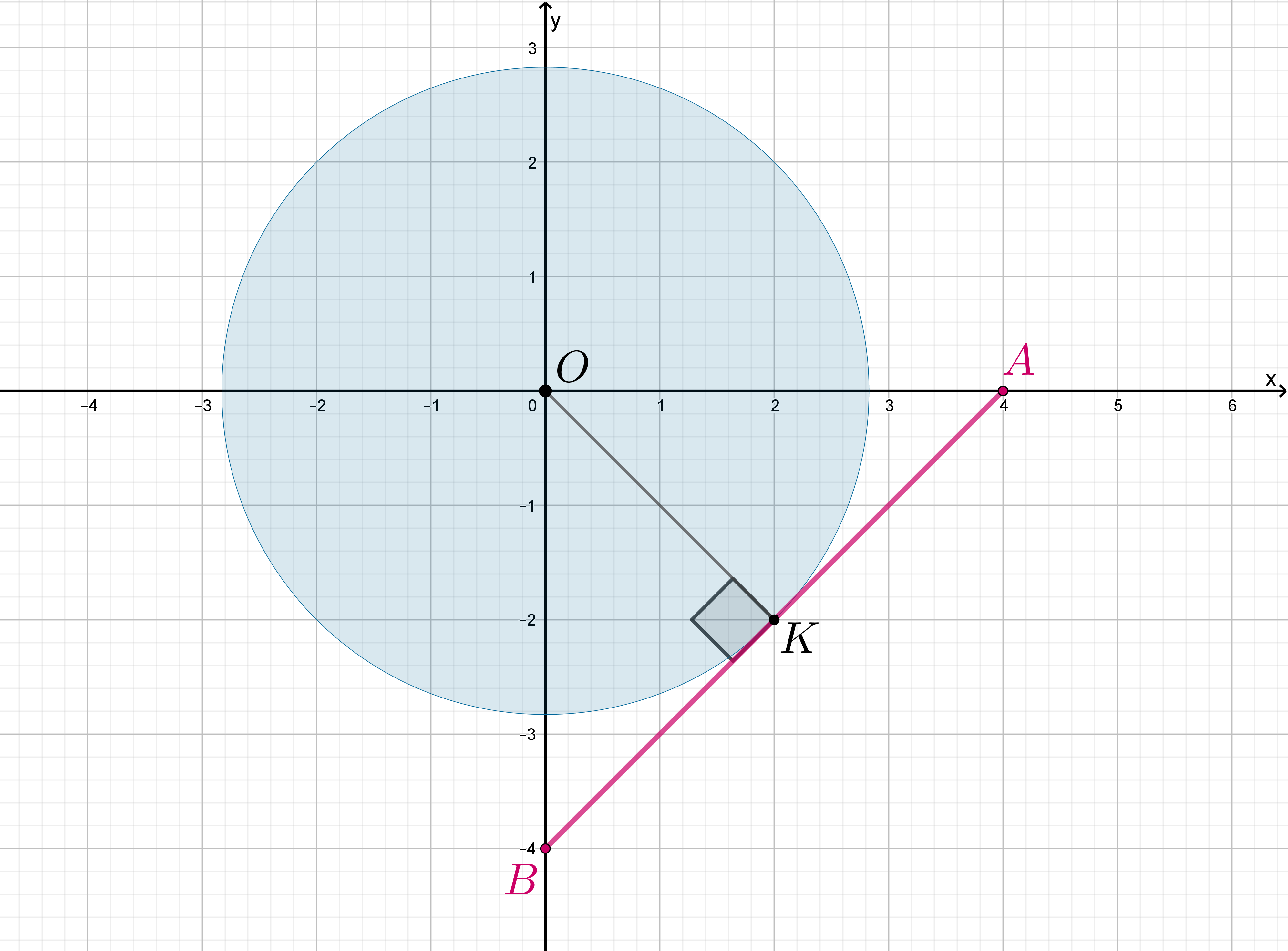
Нужно, чтобы отрезок касался окружности
(в точке
). Так как
прямоугольный и равнобедренный
(
), то
– медиана и высота, следовательно,
:
Следовательно, также подходит.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет хотя бы одно решение .
Первое равенство при фиксированном задает окружность с центром в точке
и радиусом
. Так как
, то центр
окружности при изменении
движется по окружности с центром в начале координат и радиусом
. Следовательно, при всех
первое уравнение задает множество
точек, располагающихся между окружностями с центром в
начале координат и радиусами
и
(назовем это множество “бубликом”).
Рассмотрим второе уравнение. При оно равносильно
, а при
равносильно
. Следовательно, при
оно задает квадрат, точка пересечения диагоналей которого совпадает с началом координат
, а вершины лежат на координатных
осях. При
оно задает точку
или пустое множество, что нам не подходит (точка не лежит на бублике, а пустое множество дает
пустое множество решений системы).
Рассмотрим два граничных положения для квадрата, находясь между которыми, квадрат имеет хотя бы одну точку пересечения с
бубликом, следовательно, существует такое , для которого существует окружность, с которой квадрат имеет хотя бы одну точку
пересечения, то есть существует такая тройка
:
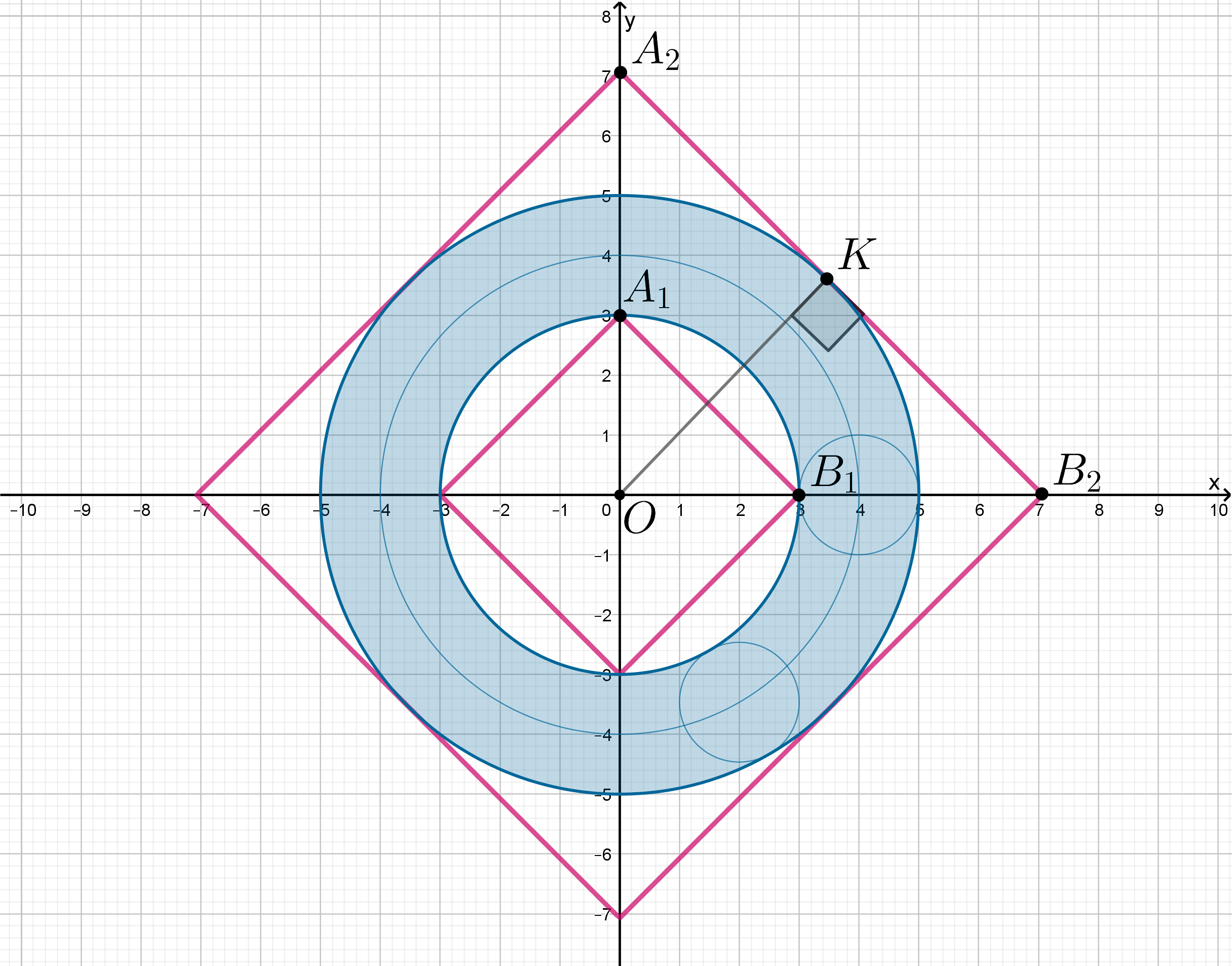
Так как половина диагонали квадрата равна , то
,
и
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых система
имеет единственное решение.
Рассмотрим первое уравнение. При оно задает точку
которая не удовлетворяет второму равенству.
Следовательно, это значение параметра нам не подходит. При
оно задает окружность с центром в точке
и радиусом
Второе уравнение при равносильно
при
равносильно
Следовательно, это уравнение задает
квадрат, диагонали которого пересекаются в точке
а вершины лежат в точках

Заметим, что — равнобедренный прямоугольный с
так как
равны диагонали единичной
клетки. Следовательно,
— точка касания окружности
и стороны
квадрата. В этом случае система имеет единственное
решение. При увеличении радиуса окружности окружность и квадрат будут иметь две точки пересечения, что нам не подходит.
Так будет происходить до тех пор, пока окружность не пройдет через вершину квадрата, не имея других общих
точек с ним. Так как расстояние от центра окружности до вершины
наибольшее, то этой точкой будет точка
Итак, для положения имеем
откуда
Для положения
имеем
откуда
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| ИЛИ | |
| не рассмотрен случай | |
| Верно рассмотрено одно из двух положений | 2 |
| ИЛИ | |
| все значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно четыре различных решения.
Сделаем замену ,
, тогда система равносильна
Данная система имеет не более четырех решений. Неизвестной не соответствует ни один
,
соответствует один
, неизвестной
соответствуют два
. Аналогично для
и
:
,
,
. Следовательно, решению
,
соответствуют два решения
(I тип), решению
,
соответствуют два решения
(I тип), а решению
,
,
соответствуют четыре решения
(II
тип).
Значит, система должна иметь либо два решения типа, либо одно решение II типа.
Исследуем второе уравнение системы. При оно задает точку, следовательно, система имеет не более одного решения, что нам не
подходит. При
оно задает пустое множество, что тоже нам не подходит. Следовательно,
. Тогда
,
. Значит, производная
Следовательно, при функция
убывает, причем заметим, что уравнение
симметрично
относительно перемены местами
и
, следовательно, график
симметричен относительно прямой
. Тогда прямая
занимает одно из положений, обозначенных на рисунке:
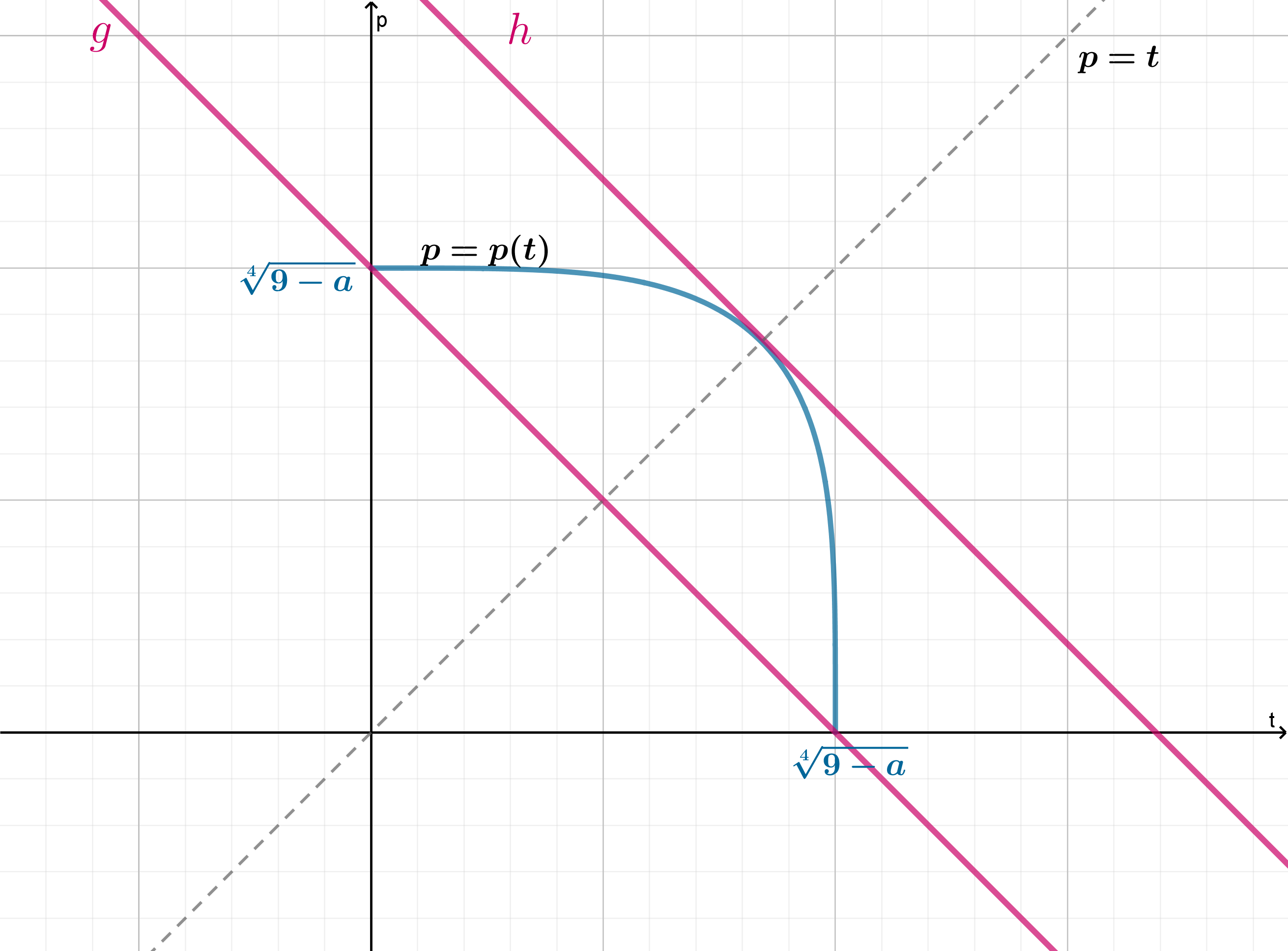
-
:
-
Прямая
проходит через
, следовательно,
-
:
-
Так как прямая
также симметрична относительно
, то точка касания для положения
прямой находится на прямой
. Следовательно,
, откуда
, тогда
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет единственное решение.
Первое равенство задает окружность с центром в точке и радиусом
Рассмотрим второе уравнение. Пусть имеются точки
Тогда второе уравнение имеет вид
следовательно, оно задет множество точек
находящихся на отрезке
Заметим, что конец
отрезка движется по оси абсцисс при изменении значений параметра
Следовательно, необходимо, чтобы отрезок имел одну точку пересечения с окружностью. Так как окружность
симметрична относительно оси ординат, а точка лежит на оси ординат, то положения
и
отрезка,
когда он касается окружности, симметричны относительно оси ординат, следовательно, если положению
соответствует
то положению
соответствует
Следовательно, рассмотрим только случай

следовательно,
Следовательно, ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Получено верно одно из двух значений
параметра | 2 |
| ИЛИ | |
| значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Первое равенство задает окружность с центром в точке и радиусом
.
Рассмотрим второе уравнение. Пусть имеются точки ,
,
. Тогда второе уравнение имеет вид
,
следовательно, оно задет множество точек
, находящихся на отрезке
. Заметим, что конец
отрезка движется по оси абсцисс при
изменении значений параметра
.
Следовательно, необходимо, чтобы отрезок имел одну точку пересечения с окружностью. Так как окружность симметрична относительно
оси ординат, а точка лежит на оси ординат, то положения
и
отрезка, когда он касается окружности, симметричны
относительно оси ординат, следовательно, если положению
соответствует
, то положению
соответствует
.
Следовательно, рассмотрим только случай
.
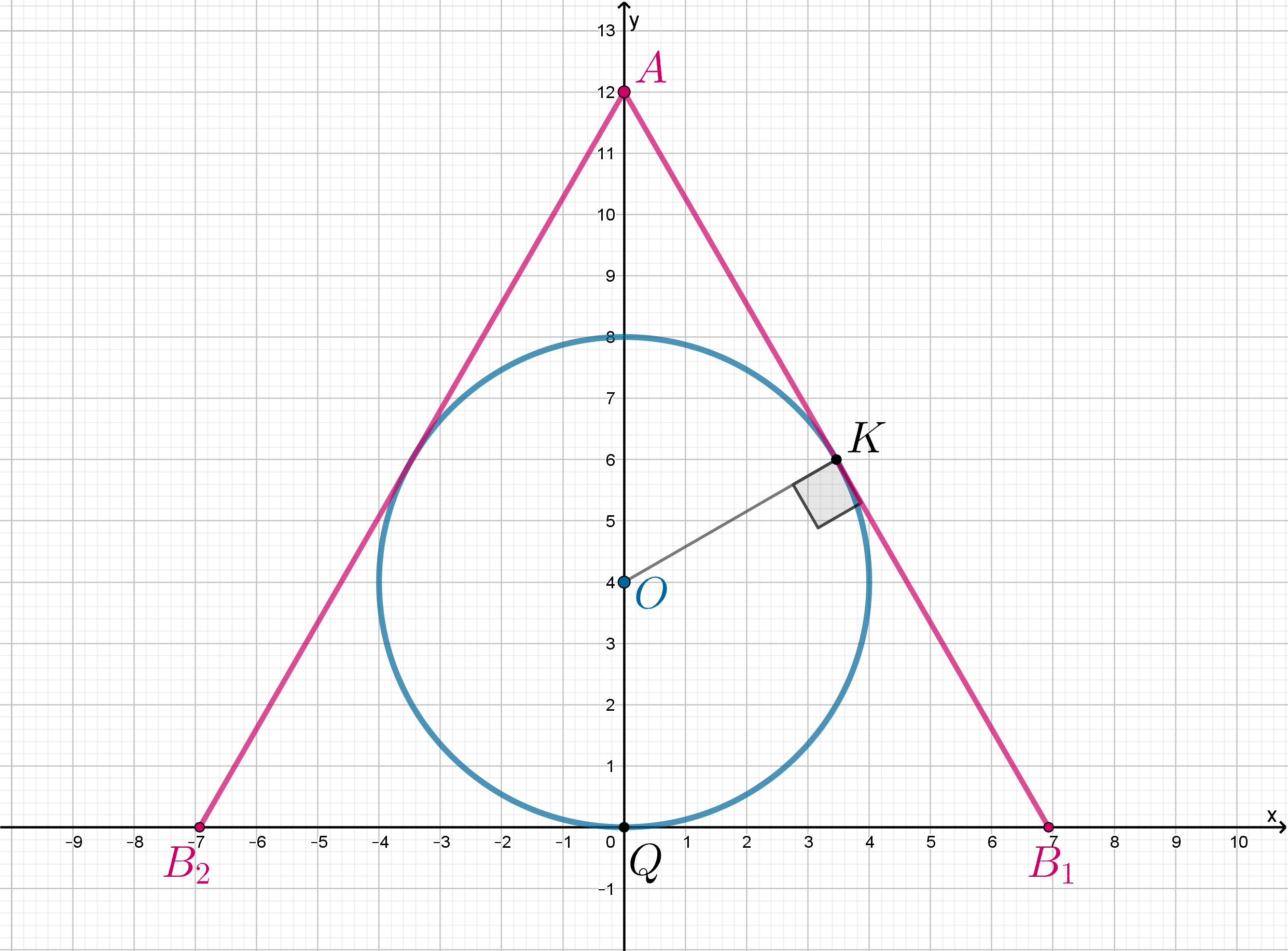
, следовательно,
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Первое уравнение системы равносильно
Следовательно, по теореме Виета ,
. Таким образом, первое уравнение задает две горизонтальные прямые,
расстояние между которыми равно
(назовем объединение этих прямых полосой).
Рассмотрим второе уравнение. Пусть имеются точки ,
,
. Тогда второе уравнение имеет вид
,
следовательно, оно задает множество точек
, находящихся на отрезке
. Заметим, что конец
отрезка движется по оси абсцисс, а
конец
отрезка движется по прямой
при изменении значений параметра
, причем при любых
отрезок параллелен оси
ординат.
Изобразим положения прямых и
, при которых они с отрезком имеют одну точку пересечения. Без ограничения общности можно
считать, что отрезок не движется горизонтально, а фиксирован в этом смысле.

Положения и
— граничные положения, при которых полоса имеет с отрезком одну общую точку. Все положения полосы
между этими (например, положение
), за исключением того положения, когда полоса проходит через концы отрезка, нам
подходят.
Следовательно, прямая ,
, откуда
,
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение параметра , при котором уравнение
имеет хотя бы одно решение.
Рассмотрим точки ,
,
,
. Тогда
Следовательно, уравнение имеет вид

где — ломаная, соединяющая две фиксированные точки
и
. Тогда смысл равенства — параметр
по значению равен
длине этой ломаной. Наименьшее значение сумма двух отрезков, выходящих из одной точки, имеет, когда эти отрезки лежат на
одной прямой, следовательно,
соответствует такой ломаной, что
*. Найдем уравнение, задающее прямую
Тогда , если
Так как система имеет решения, то возможно такое, что , следовательно,
*Заметим, что точка не может лежать на отрезке
, точка
не может лежать на отрезке
, то есть точки
отложены на прямой именно последоваптельно:
.
Ошибка.
Попробуйте повторить позже
При каждом значении решите систему:
Преобразуем второе уравнение:
Для ,
,
уравнение в системе координат
задает отрезок
, так как имеет вид
. Тогда
первое равенство равносильно
и задает в той же системе координат показательную функцию.
Таким образом, будем рассматривать параметр как переменную. Построим в системе координат
множество
решений
системы. Если некоторая точка плоскости с координатами
принадлежит этому множеству
то для исходной задачи это означает,
что если параметр
принимает значение
то
будет одним из решений системы. Нас просят решить систему при всех
, то есть
найти такие
, при которых не существует точек вида
, принадлежащих множеству
; существует одна точка такого вида,
принадлежащая множеству
; две, три и т.д. Фактически это равносильно тому, что мы ищем число точек пересечения горизонтальной
прямой
с множеством
.
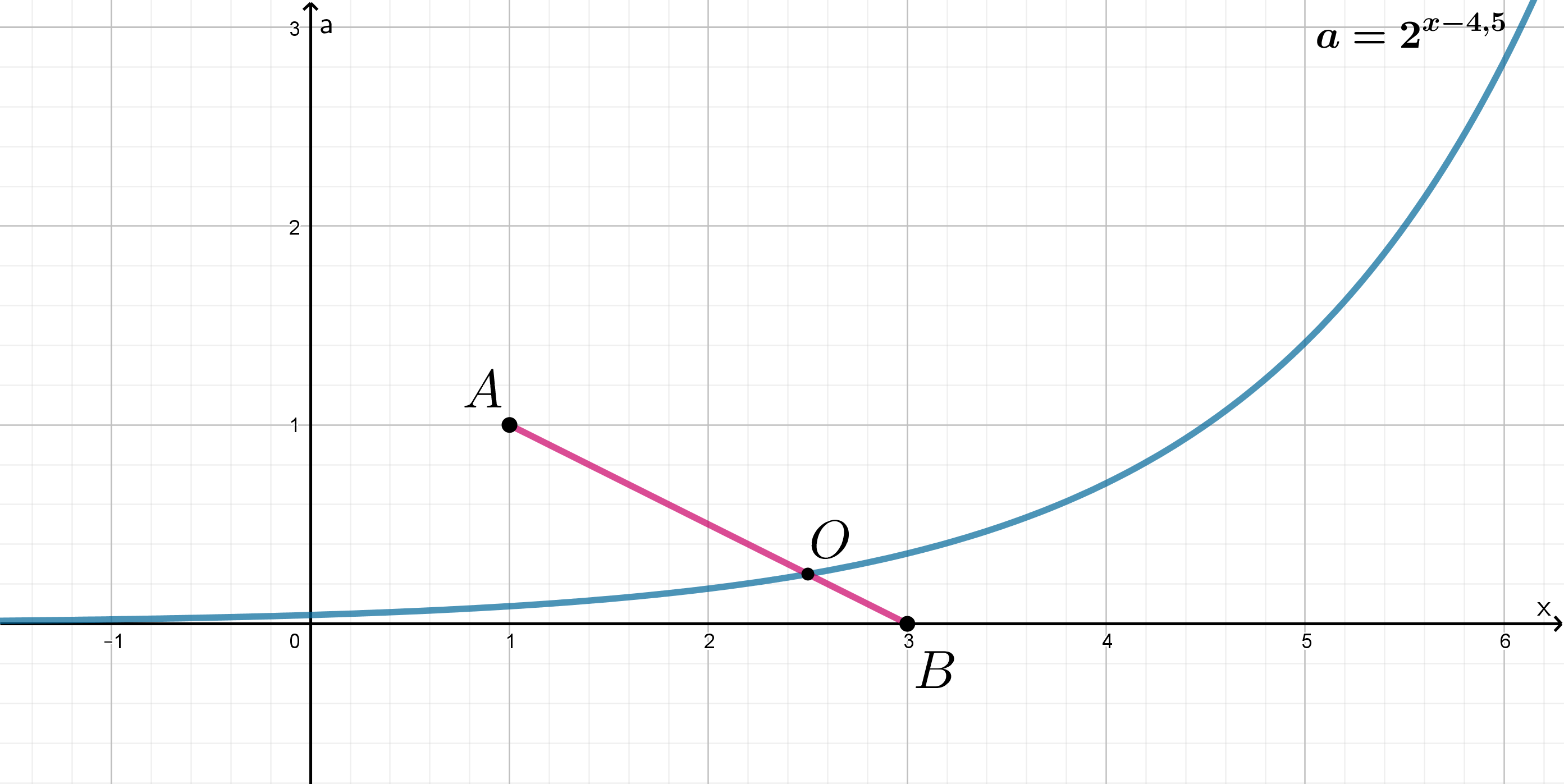
Заметим, что отрезок с графиком показательной функции имеет одну точку пересечения — точку . Следовательно, при
имеем
— решение системы, при
система не имеет решений.
Найдем уравнение прямой
Следовательно, абсцисса точки ищется из уравнения
Подбором находим, что . Тогда
Следовательно, при
решение
, при
решений
нет.
;
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно три различных решения.
Второе равенство системы можно преобразовать
Рассмотрим первое равенство. При оно равносильно
, при
равносильно
.
Следовательно, оно задает ромб
точка пересечения диагоналей которого
, то есть движется по прямой
.
Рис. 1: вершина лежит на прямой
. Так как вершина
имеет координаты
, то
, откуда
.
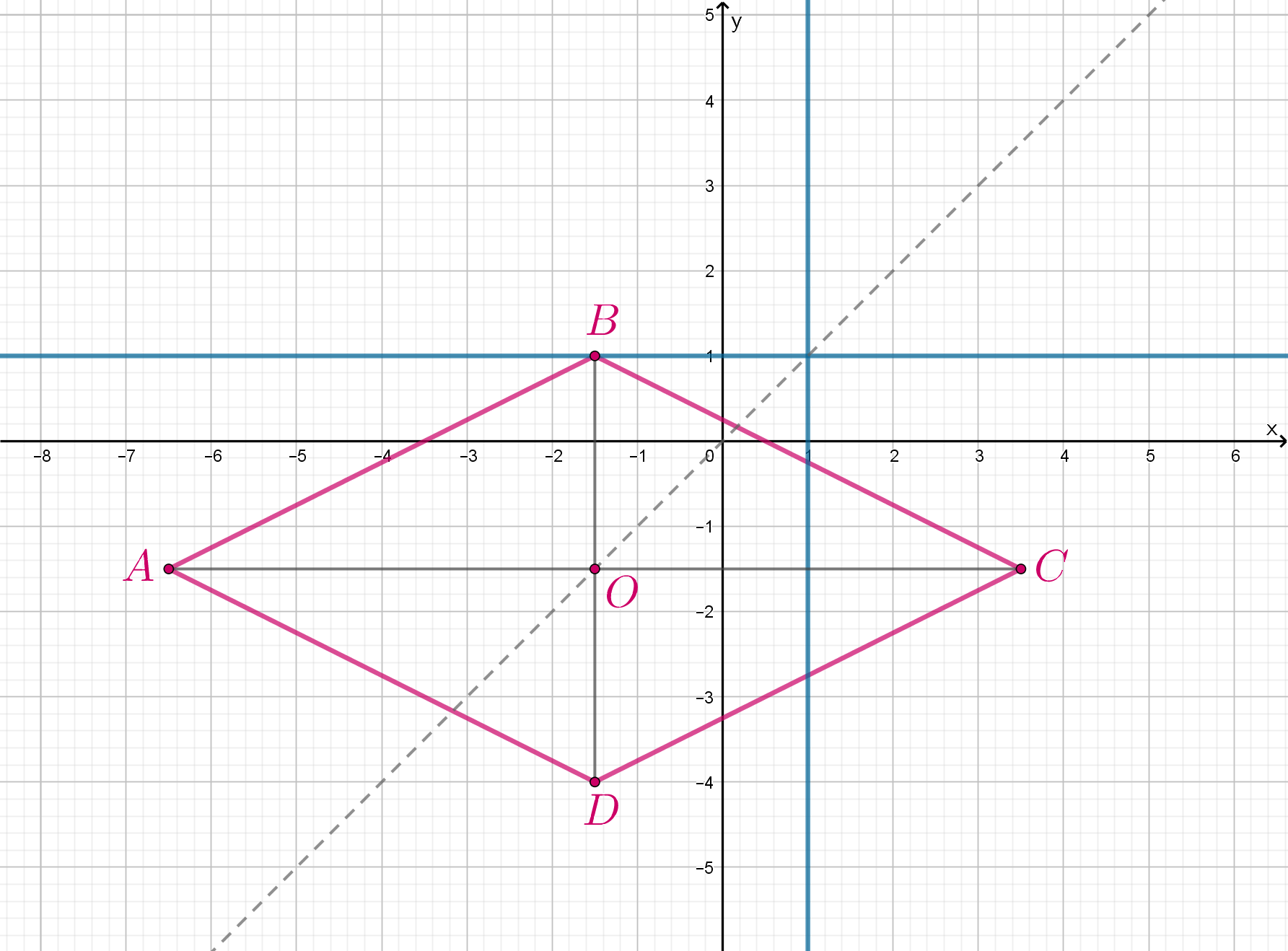
Рис. 2: точка пересечения прямых и
лежит на стороне
ромба. Сторона
лежит на правой ветви уголка
, то есть на
, следовательно,

Рис. 3: точка пересечения прямых и
лежит на стороне
ромба. Сторона
лежит на левой ветви уголка
, то есть на
, следовательно,

Рис. 4: вершина лежит на прямой
. Так как вершина
имеет координаты
, то
, откуда
.
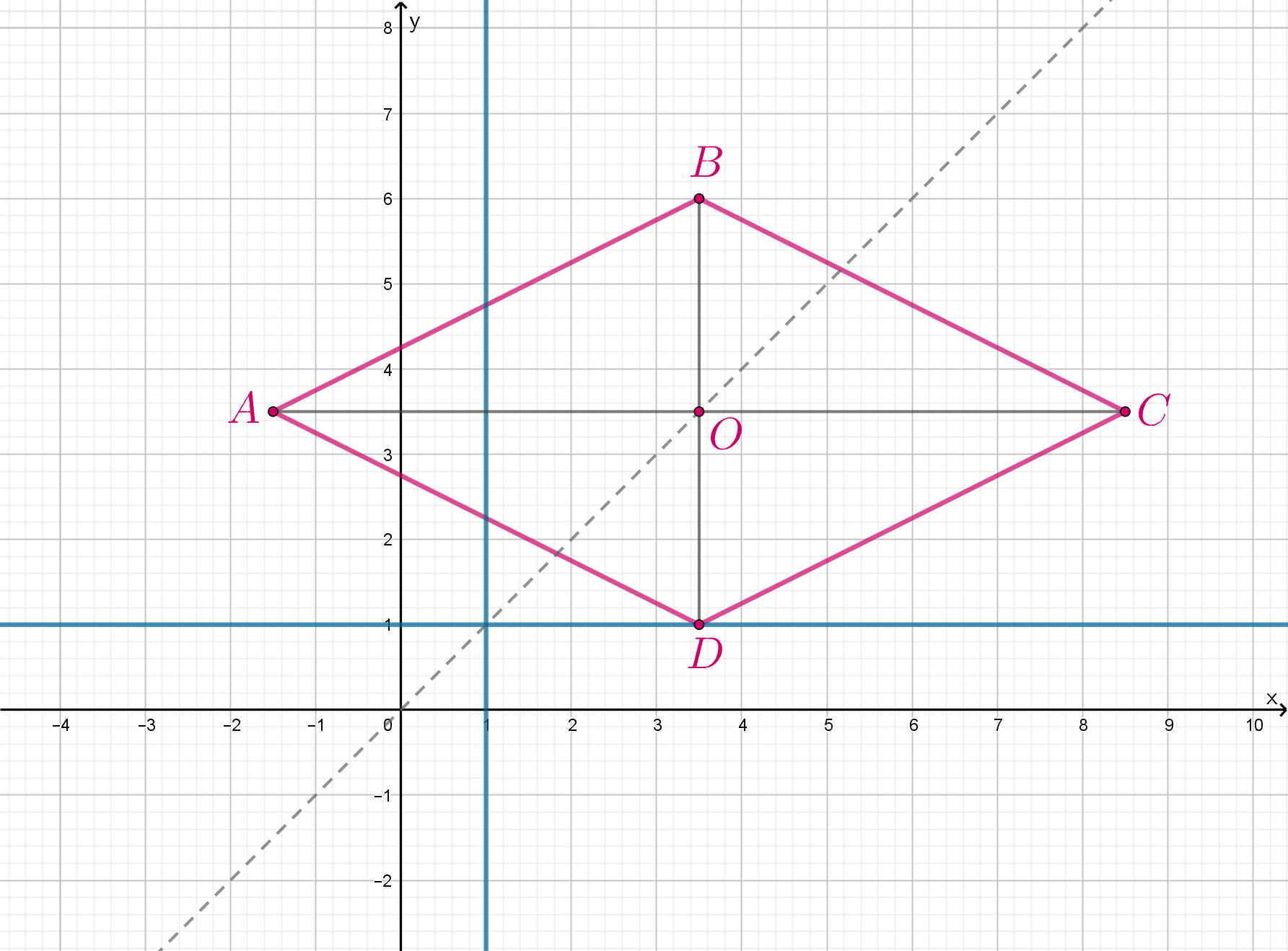
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения , при каждом из которых система
имеет ровно 2 решения.
Рассмотрим первое уравнение системы. Перепишем его в виде:
Рассмотрим второе уравнение. Заметим, что , так как в этом случае уравнение
принимает вид
, что не является верным равенством. Тогда можно переписать уравнение в
виде:
Заметим, что отрезок находится в верхней полуплоскости, следовательно, только правая ветка
гиперболы может его пересекать.
Найдем значения , при которых гипербола проходит через точку
.
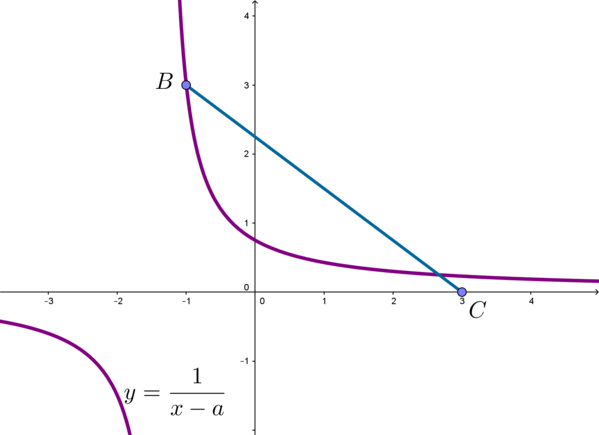
Тогда

Для этого нужно написать уравнение прямой, проходящей через точки
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система
имеет единственное решение.
Рассмотрим второе уравнение системы: оно задает семейство прямых , параллельных оси
и лежащих в верхней полуплоскости (включая ось
) при любом значении параметра
(т.к.
модуль всегда неотрицателен).
Рассмотрим первое уравнение. Пусть ,
,
– точки. Тогда
,
,
.
Таким образом, первое уравнение системы выглядит так: . Значит, оно задает
геометрическое место точек
, лежащих на отрезке
.
Для того, чтобы данная система имела единственное решение, прямая должна
пересекать отрезок
в одной точке.
1) Пусть , то есть точка
лежит на отрицательной части оси
. Единственный случай,
когда прямая
будет иметь с отрезком одну общую точку, – когда прямая
будет проходить через точку
, то есть совпадать с осью абсцисс. Отсюда
, следовательно,
. Так как
, то
.

2) Пусть . Тогда отрезок
лежит на оси абсцисс, прямая
– в верхней
полуплоскости, и общих точек у них нет.
3) Пусть . Тогда
лежит на положительном направлении оси ординат.
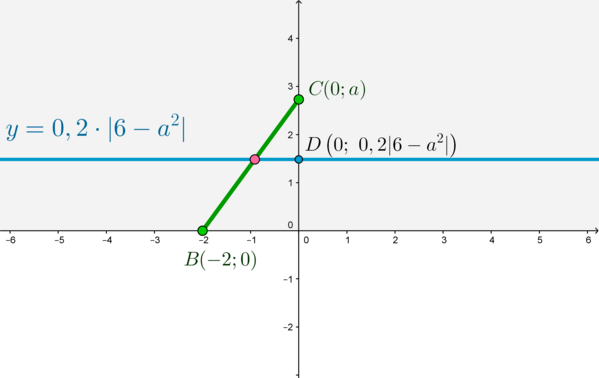
Прямая пересекает ось ординат в точке
. Для того, чтобы прямая пересекала
отрезок
, нужно, чтобы точка
находилась не ниже точки
, то есть
Решим данное неравенство. Т.к. , то имеем:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
будет иметь единственное решение.
1) Первое уравнение системы при задает отрезок
, где
,
.
Действительно, пусть . Тогда
При
2) Второе неравенство задает круг с центром в точке и радиусом
.
3) Для того, чтобы данная система имела единственное решение при , нужно, чтобы отрезок
касался круга: при
отрезок
будет находиться в четвертой четверти (рисунок 1), при
– во второй (рисунок 2).
Случай, когда , нам также подходит (так как точка
принадлежит кругу).
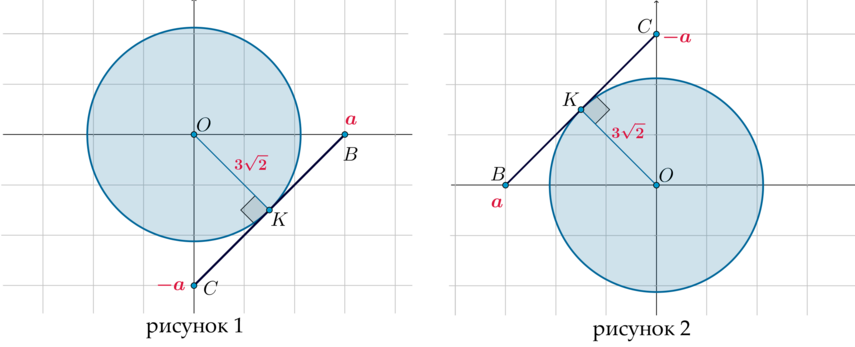
При :
– радиус, проведенный в точку касания. Тогда
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система
имеет более двух решений.
Изобразим график первого уравнения. Для этого рассмотрим следующие случаи:
1) ,
. Тогда уравнение примет вид
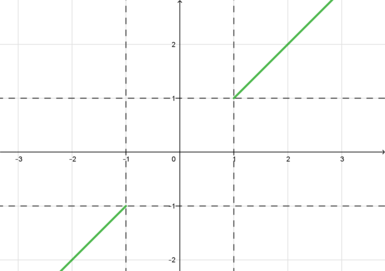
2) ,
. Тогда уравнение примет вид:
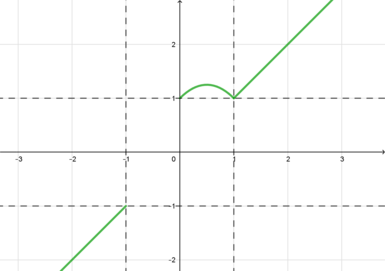
3) ,
:
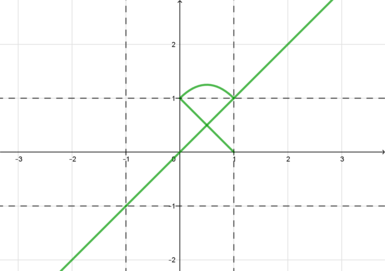
4) ,
. Тогда имеем
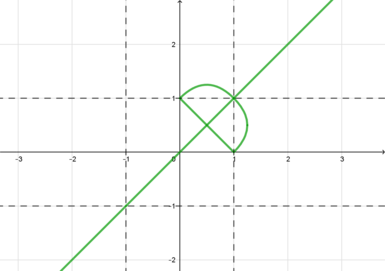
Графиком при каждом фиксированном
является прямая
, то
есть прямая, параллельная
(а также параллельная части прямой
из п.
3).
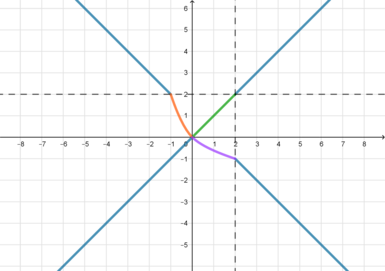
Для того, чтобы система имела более двух решений, нужно, чтобы прямая находилась в
положениях от (1) (включительно) до (2) (не включительно):

Действительно, когда прямая находится в положении (1), то система будет иметь бесконечное
множество решений (а именно, часть прямой при
); когда прямая находится между
(1) и (2), то система будет иметь 3 решения; когда прямая находится в положении (2), то система будет
иметь одно решение:
.
Прямая находится в положении (1) при
, в положении (2) – при
,
следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система
имеет более двух решений.
Изобразим график первого уравнения. Для этого рассмотрим случаи:
1) ,
. Тогда уравнение примет вид
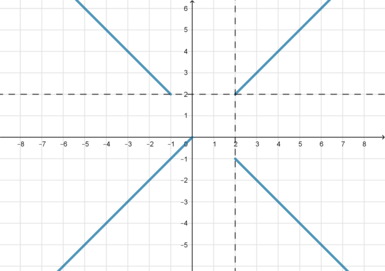
2) ,
. Тогда:
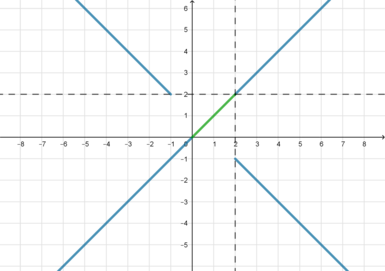
3) ,
. Тогда уравнение примет вид:
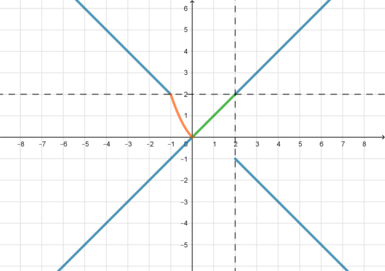
4) ,
. Тогда имеем:
Графиком при каждом фиксированном
является прямая
, то
есть прямая, параллельная
(а также параллельная части прямой
из п.
1).
Для того, чтобы система имела более двух решений, нужно, чтобы прямая находилась в
положениях от (1) (не включительно) до (2) (включительно):
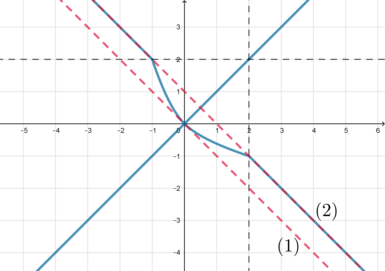
Действительно, когда прямая находится в положении (2), то система будет иметь бесконечное
множество решений (а именно, часть прямой при
, а
также точка
); когда прямая находится между (1) и (2), то система будет иметь 3
решения; когда прямая находится в положении (1), то система будет иметь одно решение:
.
Прямая находится в положении (1) при
, в положении (2) – при
,
следовательно,
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение параметра , при котором уравнение
1 способ.
Рассмотрим .
Тогда уравнение примет вид . Тогда нам нужно найти наименьшее значение
, при котором
прямая
будет пересекать график
хотя бы в одной точке. Исследуем
. Для этого
найдем сначала ее производную:
Определим знаки производной:

Следовательно, схематично график функции выглядит так:
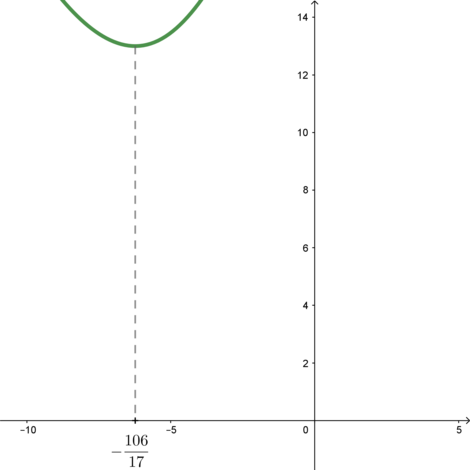
Следовательно, наименьшее значение параметра – когда прямая
проходит через точку
экстремума функции
:
2 способ.
Заметим, что в первом способе было очень много вычислений и на самом деле нам повезло, что при
решении уравнения слагаемые с
и
взаимно уничтожились и мы пришли к квадратному
уравнению. А что делать, если числа так хорошо не подобраны и мы не получим в конечном итоге
“красивое” уравнение, которое сможем решить?
Давайте рассмотрим второй способ решения подобных уравнений.
Рассмотрим три точки: ,
,
. Тогда уравнение примет вид
Где располагается точка
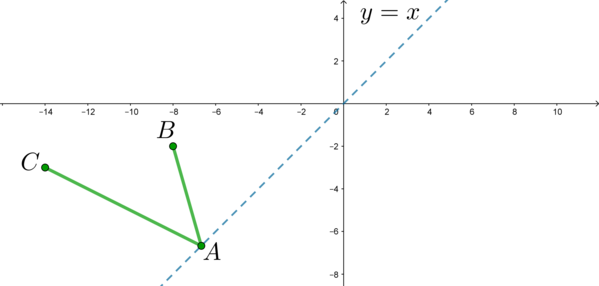
Здесь мы будем использовать классическую идею планиметрии. Отразим симметрично точку

Тогда

Таким образом, мы идейно поняли, где должна находиться точка
1) Найдем координаты точки .
Для этого сначала найдем уравнение прямой . Так как
, то если уравнение прямой
имеет вид
, то
(произведение угловых коэффициентов двух взаимно
перпендикулярных прямых равно
). Следовательно,
.
Для того, чтобы найти число , нужно подставить координаты точки
в уравнение прямой:
Найдем координаты точки
2) Найдем уравнение прямой . Если уравнение этой прямой в общем виде выглядит как
, то
3) Теперь можно найти значение параметра .
Чем хорош этот способ? Во-первых, он более изящный. Во-вторых, в ходе решения мы сталкивались только с линейными уравнениями, которые решать намного проще.



