04 Законы сохранения в механике
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
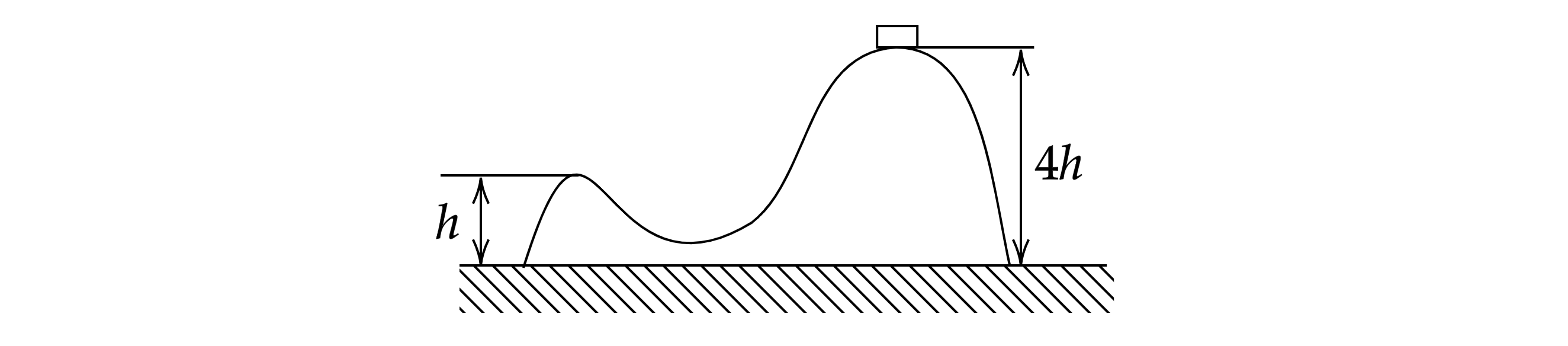
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых и
(см.
рисунок). На правой вершине горки находится шайба. Масса горки в 8 раз больше массы шайбы. От незначительного
толчка шайба и горка приходят в движение, причем шайба движется влево, не отрываясь от гладкой поверхности
горки, а поступательно движущаяся горка не отрывается от стола. Найдите скорость шайбы на левой вершине горки.
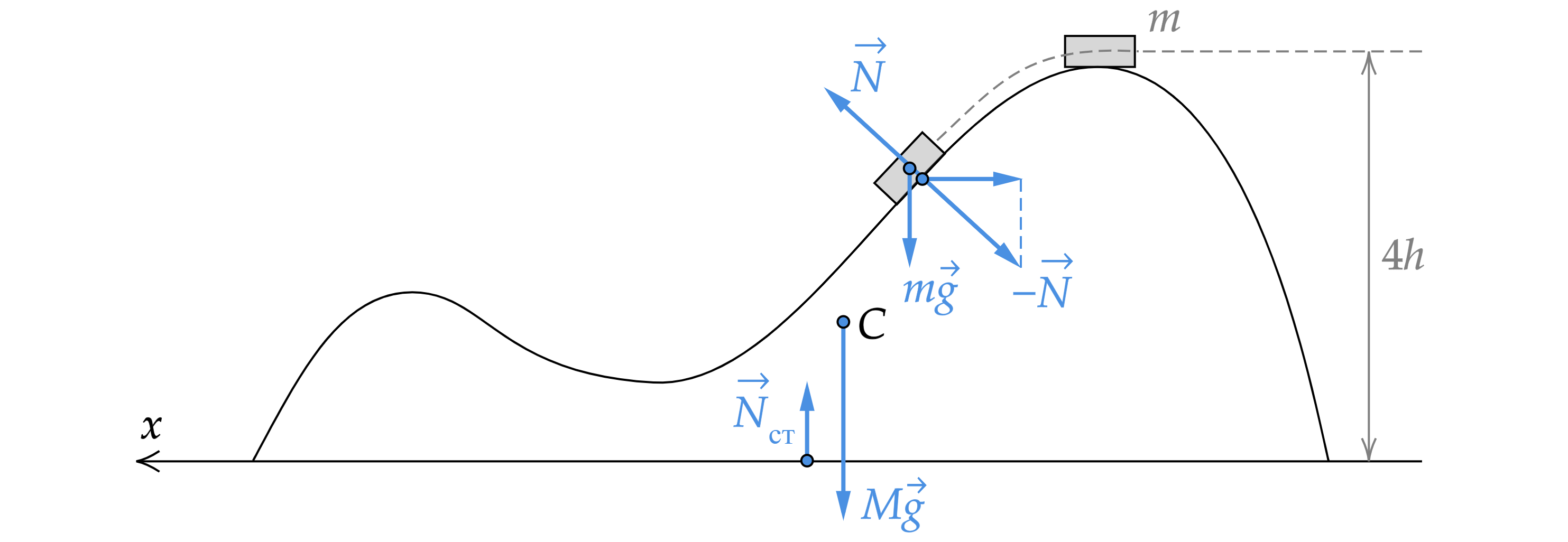
Пусть – масса шайбы,
– масса горки,
– скорость горки.
Потенциальная тела массой на высоте
равна
а кинетическая энергия тела со скоростью и массой
На систему действуют внешние силы, а именно сила реакции опоры и сила тяжести, но они направлены вертикально, поэтому можем записать закон сохранения импульса на горизонтальную ось, приняв начальную положение за начало движения, а нахождения шайбы на второй вершине горки за конечное, с учетом, что изначально все тела покоились
где – импульс шайбы,
– импульс горки.
Для системы "горка+ шайба"выполняется закон сохранения энергии
Из закона сохранения импульса имеем
Подставим (2) в (1) и умножим обе части на 2
Отсюда
Дополнение к задаче
Запишем закон об изменении полной механической энергии
Рассмотрим горку, по которой скользит тело со скоростью относительно горки, а горка движется со скоростью
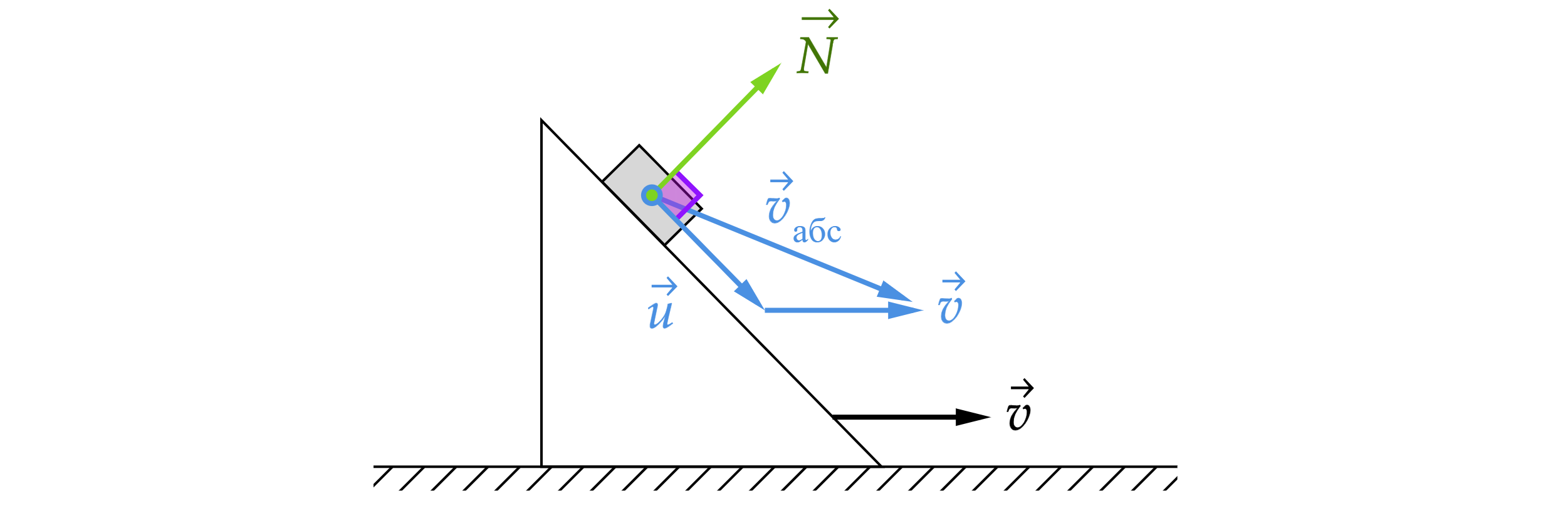
Рассмотрим суммарную мощность двух сил
Так как , то суммарная мощность
Так как суммарная мощность равна нулю, то суммарная работа равна нулю и в задаче можно применить закон сохранения энергии.
Критерии проверки
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии,
закон сохранения импульса);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии
задачи);
III) проведены необходимые математические преобразования, приводящие к правильному
ответу;
IV) представлен правильный ответ
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования. Но имеются следующие недостатки.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
ИЛИ
В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.)
ИЛИ
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца.
ИЛИ
Отсутствует пункт IV, или в нём допущена ошибка
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на
решение задачи, и ответа.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
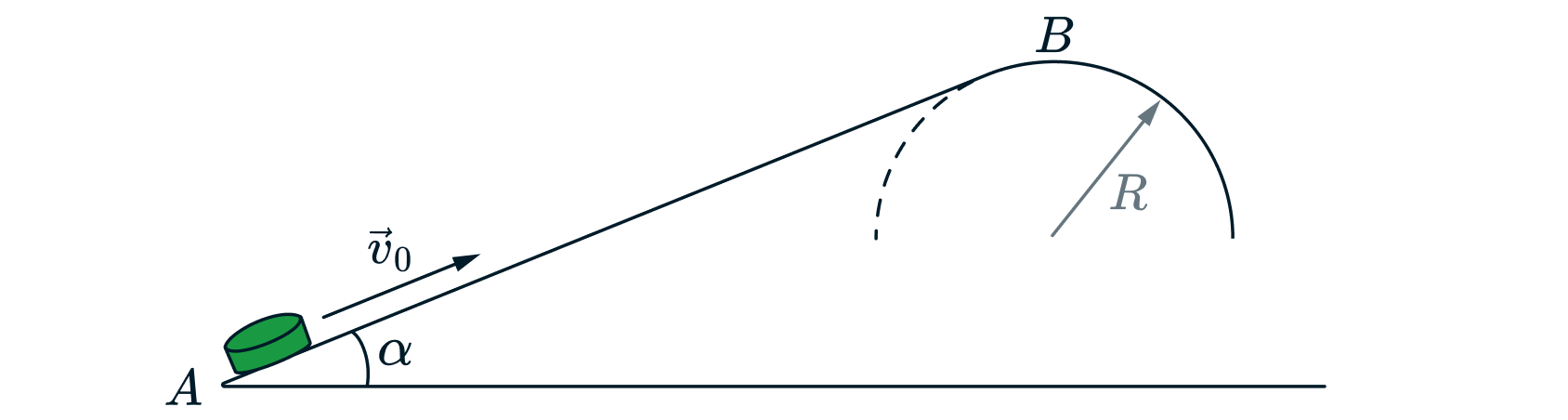
Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А. В точке В наклонная плоскость без излома
переходит в наружную поверхность горизонтальной трубы радиусом Если в точке А скорость шайбы превосходит
то в точке В шайба отрывается от опоры. Длина наклонной плоскости
угол
Коэффициент трения
между наклонной плоскостью и шайбой
Найдите длину наклонной плоскости
. Обоснуйте применимость законов,
используемых для решения задачи.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО), связанную с землей.
2. Шайба движется поступательно, поэтому её можно считать материальной точкой.
3. Так как груз является материальной точкой, то описывать его движение в ИСО будем, используя законы Ньютона.
4. Когда тело начинает двигаться по закруглению, оно начинает двигаться с центростремительным ускорением, направленным к
центру окружности вращения.
5. В момент отрыва тело не взаимодействует с опорой, а значит сила нормальной реакции опоры, действующая на тело обращается в
нуль
6. Связать положения тела в пространстве можно через теорему об изменении кинетической энергии, поскольку на тело действует
сила трения, уменьшающая энергию. При этом работа силы нормальной реакции опоры равна нулю, так как сила перпендикулярна
вектору перемещения
Решение
На тело при движении действует сила тяжести , сила нормальной реакции опоры
и сила трения
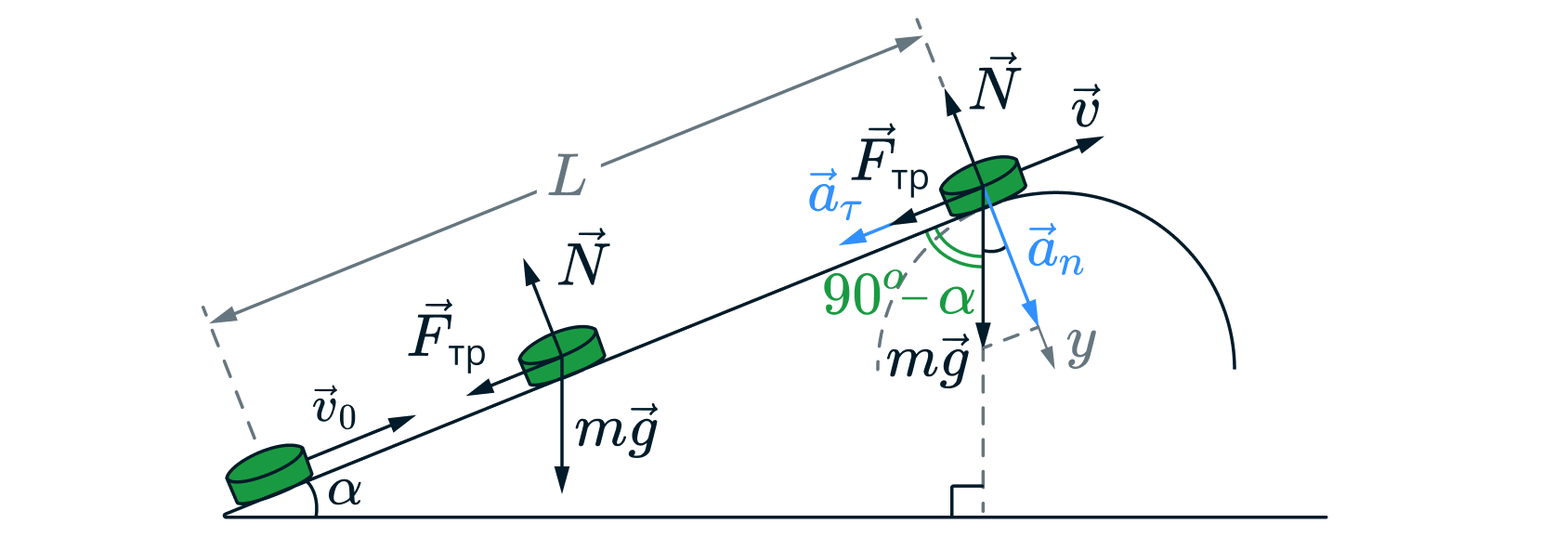
Запишем второй закон Ньютона
В проекции на ось
где – центростремительное ускорение.
значит
При этом, пока тело движется по прямой и
, тогда сила трения равна
В момент отрыва , значит
Запишем теорему об изменении кинетической энергии
Отсюда
Отсюда
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к шайбе модели материальной точки
3. Обосновано применение формулы второго закона Ньютона
4. Обосновано применение закона сохранения энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное правильное решение, включающее следующие элементы:
— верно записаны формулы, выражающие физические законы, применение которых необходимо для
решения задачи выбранным способом (в данном решении — изменение механической энергии тела за
счет работы сил трения, формула для центростремительного ускорения при движении по
окружности);
— проведены необходимые математические преобразования и расчеты, приводящие к правильному
числовому ответу, и представлен ответ. При этом допускается решение "по частям"(с промежуточными
вычислениями).
2 балла ставится если:
_________________________________________________________________________________________________________________
— Представлено правильное решение только в общем виде, без каких-либо числовых расчетов.
ИЛИ
— Правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу.
ИЛИ
— В математических преобразованиях или вычислениях допущена ошибка, которая привела к неверному ответу.
1 балл ставится если:
_________________________________________________________________________________________________________________
– В решении содержится ошибка в необходимых математических преобразованиях и отсутствуют
какие-либо числовые расчеты.
ИЛИ
Записаны все исходные формулы, необходимые для решения задачи, но в ОДНОЙ из них допущена ошибка.
ИЛИ
Отсутствует одна из формул, необходимых для решения задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла (использование неприменимого закона, отсутствие более одного исходного уравнения, разрозненные записи и т.п.).
Ошибка.
Попробуйте повторить позже
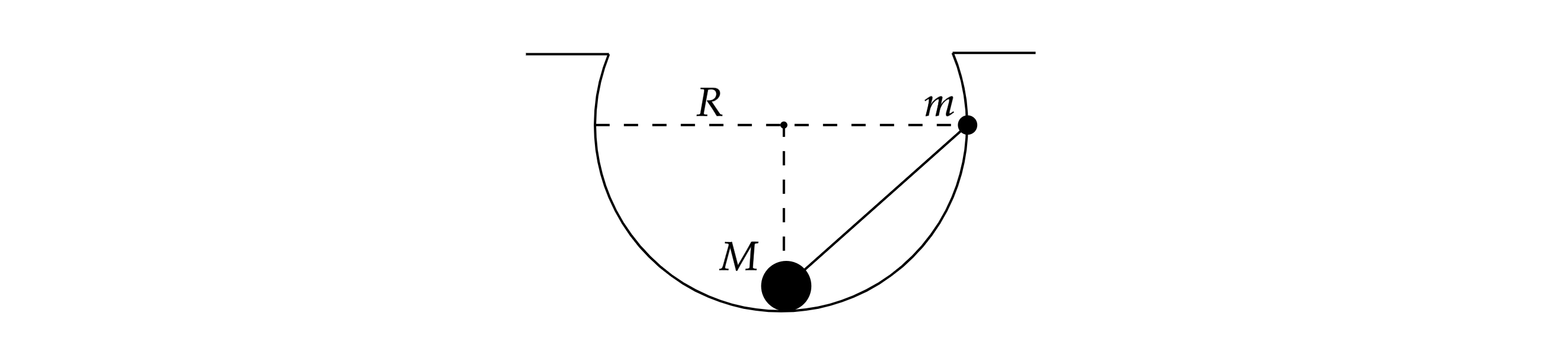
Небольшие шарики, массы которых г и
г, соединены легким стержнем помещены в гладкую сферическую выемку.
В начальный момент шарики удерживаются в положении, изображенном на рисунке. Когда их отпустили без толчка, шарики стали
скользить по поверхности выемки. Максимальная высота подъема шарика массой
относительно нижней точки выемки
оказалась равной 12 см. Каков радиус выемки
? Обоснуйте применимость законов, используемых для решения
задачи.
Источники:
Обоснование
1. Задачу будем решать в лабораторной инерциальной системе отсчёта, связанной с неподвижной выемкой.
2. Шарики будем считать материальными точками, стержень нерастяжимым.
3. Трением о воздух пренебрегаем. Включим в систему тел шарики и Землю.
4. Поскольку выемка гладкая и работа сил нормальной реакции стенок, в любой момент времени перпендикулярных скорости шариков, равна нулю, полная механическая энергия системы сохраняется.
Решение
Полная механическая энергия системы, равная сумме кинетической и потенциальной энергии, сохраняется, так как выемка гладкая и работа сил реакции стенок, в любой момент времени перпендикулярных скоростям шариков, равна нулю:
В начальный момент и момент подъёма на максимальную высоту кинетическая энергия системы равна нулю, поэтому её
потенциальная энергия в эти моменты времени одинакова:
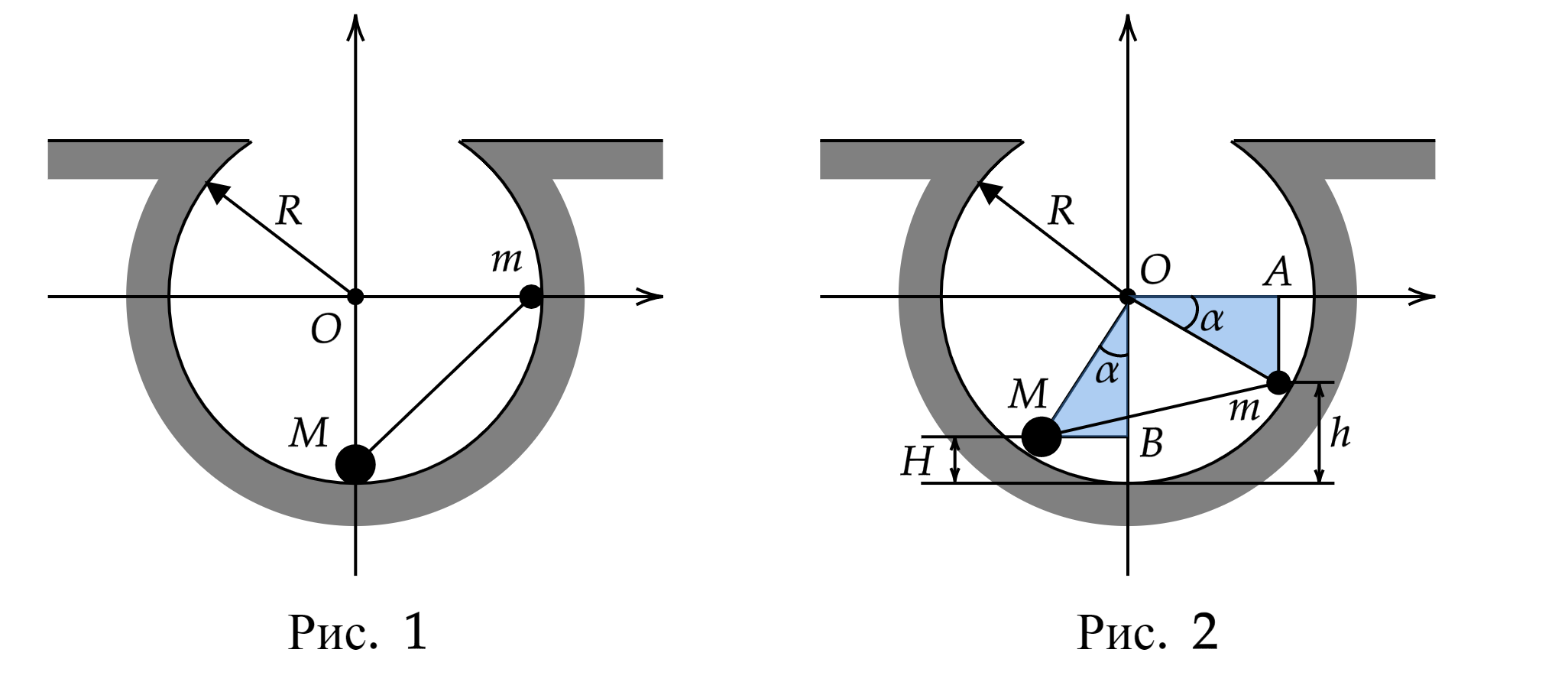
Начальное положение системы изображено на рис. 1, а конечное – на рис. 2. Если отсчитывать потенциальную энергию от
нижней точки выемки, то начальная потенциальная энергия системы , а её конечная потенциальная энергия
. Закон сохранения энергии приводит к уравнению
из которого следует, что
При движении гантели по поверхности выемки высоты подъёма большого и малого грузов связаны. Заметим, что в
прямоугольных треугольниках и
,
,
,
, и воспользуемся
теоремой Пифагора:
Подставим сюда выражение , полученное из закона сохранения энергии, и получаем:
Подставляя сюда значения физических величин, получим:
Критерии проверки
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения механической
энергии);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии
задачи);
III) проведены необходимые математические преобразования и расчеты, приводящие к правильному
числовому ответу (допускается решение «по частям» с промежуточными вычисле- ниями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования. Но имеются следующие недостатки.
Записи, соответствующие пункту II, представлены не в полном объеме или отсутствуют.
ИЛИ
В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачеркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/ вычисления не доведены до конца
И (ИЛИ)
Отсутствует пункт IV, или в нем допущена ошибка
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
Два шарика, массы которых отличаются в 3 раза, висят, соприкасаясь, на вертикальных нитях (см. рис.). Легкий шарик отклоняют
на угол и отпускают из состояния покоя. Каким будет отношение кинетических энергий тяжелого и легкого шариков тотчас
после их абсолютно неупругого центрального удара?
Основная волна 2017

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шары движутся поступательно, поэтому их можно считать материальными точками.
3. Так как время столкновения шаров пренебрежимо мало, выполняется закон сохранения импульса.
Решение
Кинетическая энергия тела находится по формуле:
где – масса тела,
– его скорость.
Запишем закон сохранения импульса в момент, когда происходит удар
где – импульс налетающего шара
– импульс составного тела после столкновения,
– скорость после
столкновения.
Спроецируем на горизонтальную ось
Тогда кинетические энергии шаров
Ошибка.
Попробуйте повторить позже
Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна 500 м/с. В точке максимального, подъема снаряд разорвался на два осколка. Первый упал на землю вблизи точки выстрела, имея скорость в 2 раза больше начальной скорости снаряда, а второй в этом же месте — через 100 с после разрыва. Чему равно отношение массы первого осколка к массе второго осколка? Сопротивлением воздуха пренебречь. Обоснуйте применимость законов, используемых для решения задачи.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Снаряд движется поступательно, будем считать его материальной точкой.
3. По условию задачи сопротивление воздуха равно нулю, а значит, применим закон сохранения энергии для описания движения тела.
4. Момент разрыва можно считать мнгновенным, действие внешних сил намного меньше внутренних, применим закон сохранения импульса.
5. Движение второго осколка можно считать равноускоренным, за счет постоянной силы тяжести. Его движение будем описывать при помощи формул кинематики равноускоренного движения.
Решение
Кинетическая энергия тела находится по формуле:
где – масса тела,
– его скорость.
Потенциальная энергия равна
где – высота подъёма.
По закону сохранения энергии
где – начальная скорость снаряда.
При разрыве снаряда и движении первого осколка также выполняется закон сохранения энергии
Начальную скорость второго осколка найдем из кинематики в момент падения
где – время полета второго осколка.
Отсюда . В момент разрыва импульс сохраняется, значит, Запишем закон сохранения импульса в момент, когда
происходит удар
где – импульс снаряда
и
– импульсы первого и второго осколков соответственно.
Проецируем на вертикальную ось
Ошибка.
Попробуйте повторить позже
С какой высоты надо бросить вниз мяч, чтобы он после удара о землю подпрыгнул на высоту 2,7 м, если известно, что при ударе модуль импульса мяча уменьшается на 25%? Начальная скорость мяча 5 м/с. Сопротивление воздуха пренебречь. Обоснуйте применимость законов, используемых для решения задачи.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Движение тела является поступательным, будем считать его материальной точкой.
3. По условию задачи сопротивлением воздуха пренебрегаем, значит, выполнаяется закон сохранения энергия для движения тела.
Решение
Кинетическая энергия тела находится по формуле:
где – масса тела,
– его скорость.
Потенциальная энергия равна
где – высота подъёма.
По закону сохранения энергии
где – скорость мяча до удара,
– начальная скорость мяча.
Импульс равен
Так как в момент удара импульс уменьшается на 25%, то скорость мяча после удара о землю . При движении вверх
опять выполняется закон сохранения энергии
где – высота подъёма шара после соударения.
Тогда
Ошибка.
Попробуйте повторить позже
Небольшая шайба после толчка приобретает скорость м/с и скользит по внутренней поверхности гладкого закрепленного
кольца радиусом
= 0,14 м. На какой высоте
шайба отрывается от кольца и начинает свободно падать? Обоснуйте
применимость законов, используемых для решения задачи.
Основная волна 2016
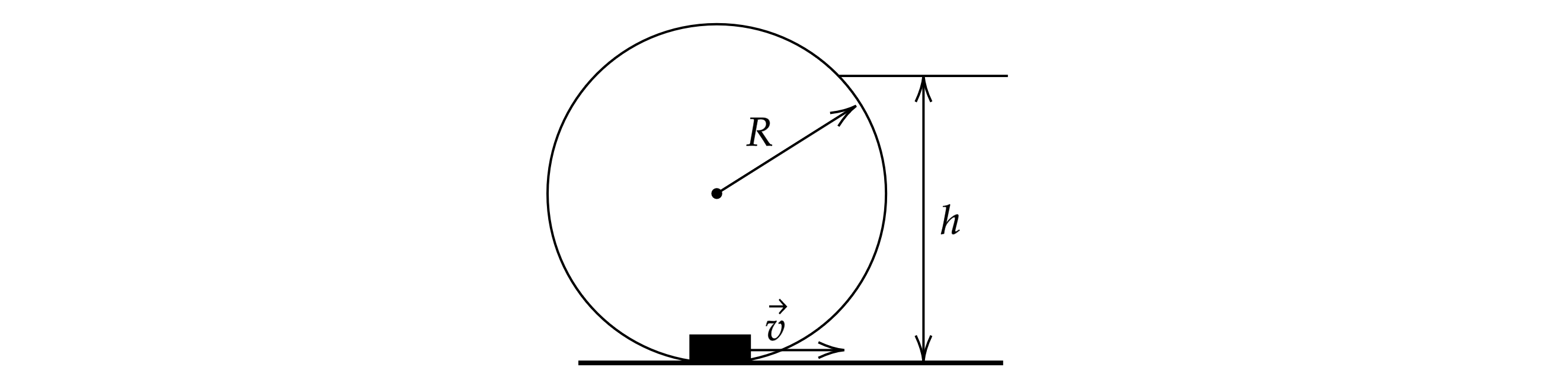
Источники:
Обоснование
1. Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать эту систему отсчета инерциальной (ИСО).
2. Шайбу описываем моделью материальной точки, так как ее размерами по сравнению с кольцом можно пренебречь.
3. При движении шайбы по поверхности кольца на нее действуют потенциальная сила тяжести и сила реакции опоры со стороны кольца, перпендикулярная его поверхности. Работа силы реакции опоры при движении шайбы равна нулю, сила трения отсутствует. Тогда в ИСО сохраняется механическая энергия.
4. Поскольку шайба описывается моделью материальной точки, условие отрыва этого тела от поверхности кольца формируется на основе второго закона Ньютона. В момент отрыва обращается в ноль сила реакции опоры. Для материальной точки применимы законы движения по окружности.
Решение
Для того, чтобы шайба оторвалась от поверхности, сила реакции опоры должна быть равна 0, тогда по второму закону Ньютона
Учитывая, что , получаем
Также запишем закон сохранения энергии
Ошибка.
Попробуйте повторить позже
Горизонтальная поверхность разделена на две части: гладкую и шероховатую. На границе этих частей находится небольшой кубик.
Со стороны гладкой части на него налетает по горизонтали шар массой г, движущийся со скоростью
м/с.
Определите массу кубика m, если он остановился после абсолютно упругого центрального соударения с шаром на расстоянии
м от места столкновения. Коэффициент трения кубика о поверхность
. Обоснуйте применимость законов, используемых для
решения задачи.
1. Кубик и шар считаем материальными точками, не учитываем энергию вращения шара после удара и процесс перехода кубика с
гладкой части на шероховатую.
2. Так как соударение абсолютно упругое, то можно записать закон сохранения импульса и механической энергии для шара и
кубика:
|
|
где – скорость кубика;
– скорость шара сразу после удара. 3. Из этих выражений получаем:
.
4. Для описания движения кубика после удара до остановки можно, например, воспользоваться законом изменения механической
энергии:
5. Объединяя полученные выражения, получаем:
Ошибка.
Попробуйте повторить позже
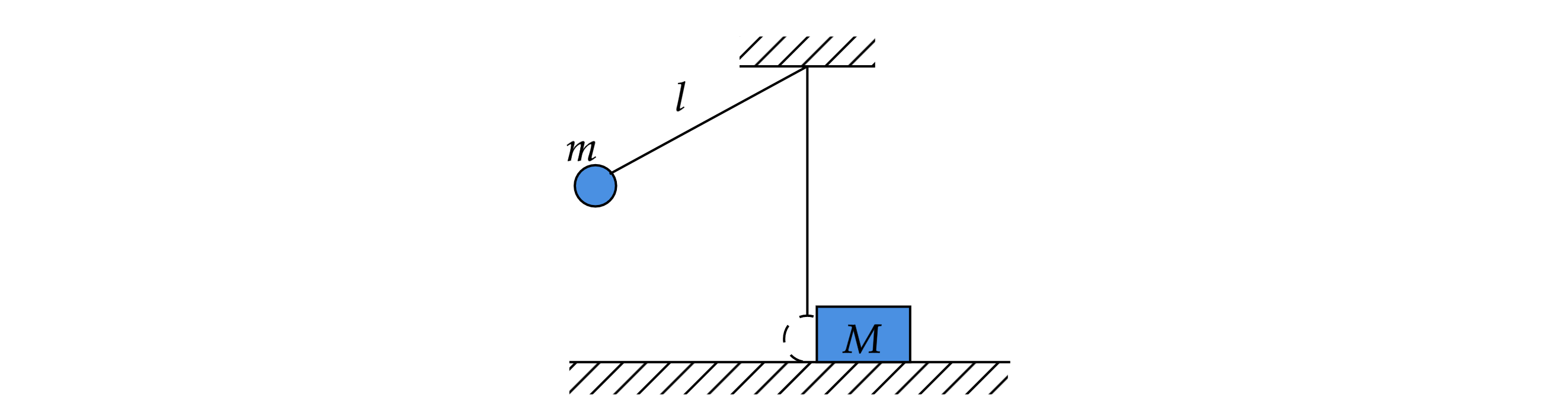
Маленький шарик массой кг подвешен на лёгкой нерастяжимой нити длиной
м, которая разрывается при силе
натяжения
Н. Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и отпущен. Когда шарик
проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго сталкивается с бруском массой
кг,
лежащим неподвижно на гладкой горизонтальной поверхности стола. Какова скорость
бруска после удара? Считать, что брусок
после удара движется поступательно.
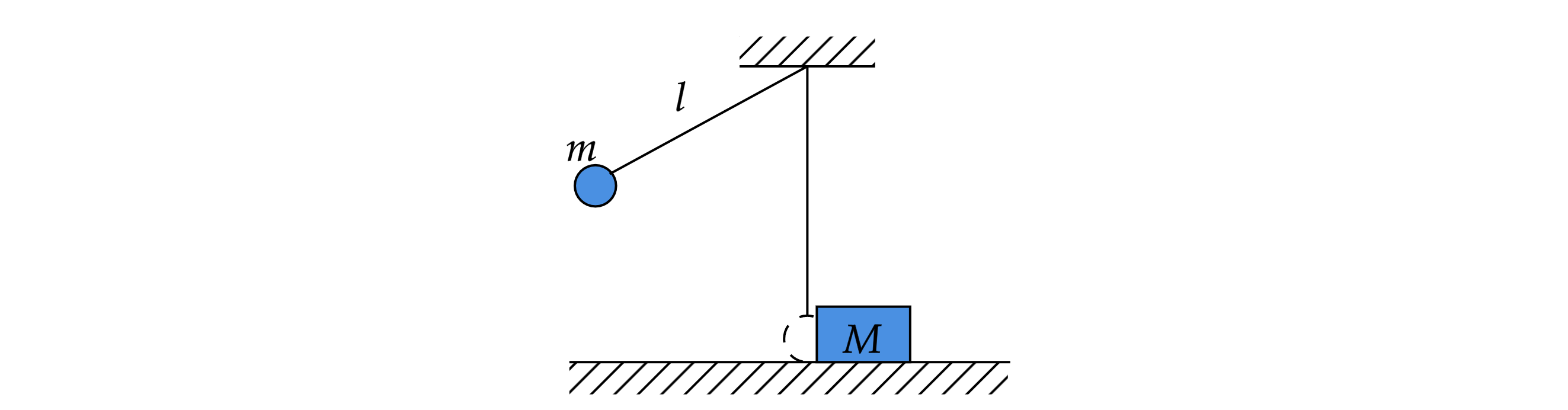
Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО), связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью
материальной точки.
3. Будем считать, что время соударения мало, и действие внешних сил во много раз меньше сил внутренних, поэтому момент
соударения будем описывать с использованием закона сохранения импульса.
4. Поскольку шар является материальной точкой, его движение в ИСО будем описывать при помощи второго закона
Ньютона.
5. Поскольку шар движется по дуге окружности радиуса , он будет обладать центростремительным ускорением, направленным к
центру окружности.
Решение
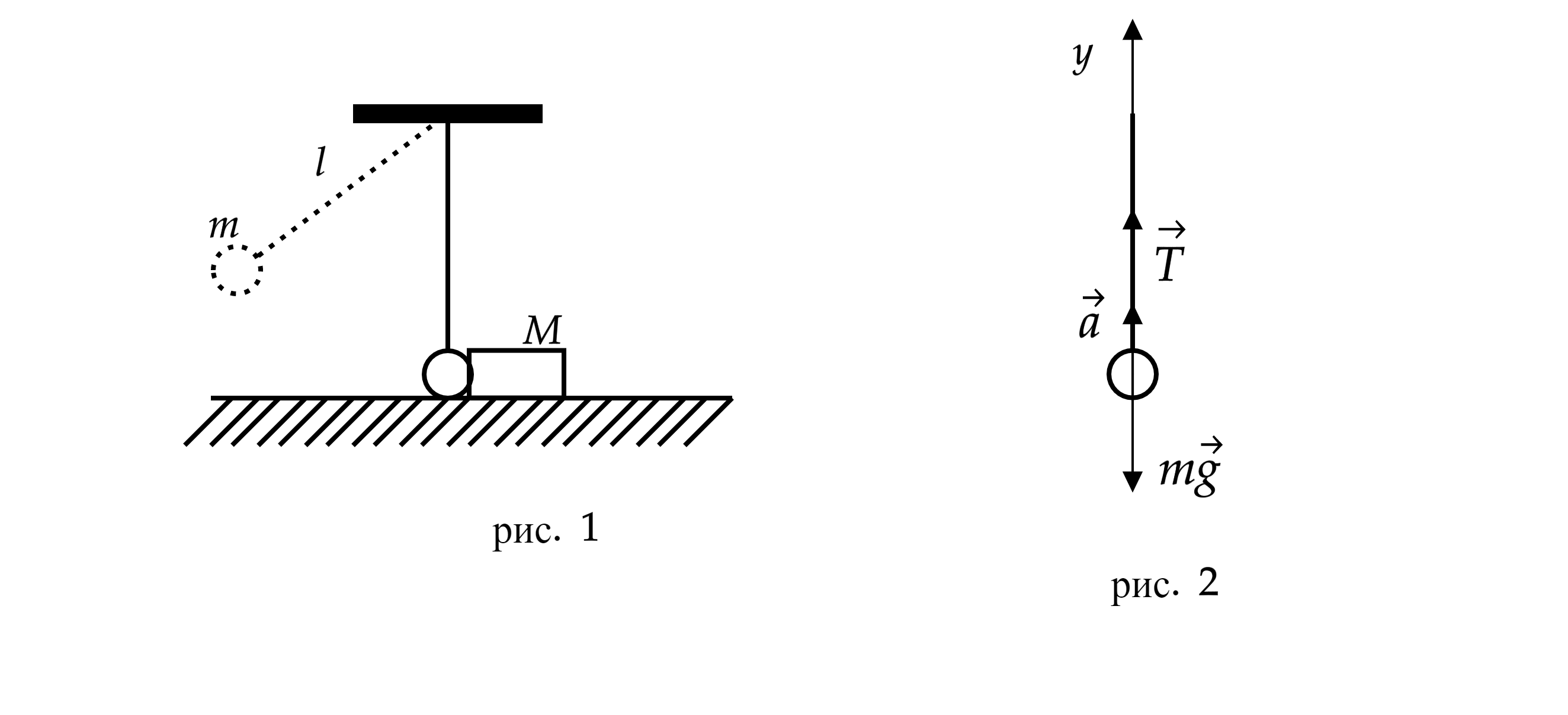
Запишем второй закон Ньютона в момент, когда шарик касается бруска (см. рис. 2)
где - полное ускорение.
В проекции на вертикальную ось, направленную вверх
где – сила тяжести,
– центростремительное ускорение,
– скорость шарика.
Распишем все составляющие закона по формулам и получим:
– скорость перед столкновением с бруском. Выразим скорость перед столкновением
Также запишем закон сохранения импульса при абсолютно неупругом ударе
где – импульс шарика,
– импульс бруска,
– импульс бруска и шарика после удара. Распишем все составляющие по
формулам, с учетом того, что брусок покоится
Выразим искомую скорость
Подставим (1) в (2)
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность описания шарика моделью материальной точки
3. Обосновано применение второго закона Ньютона для описания движения шарика
4. Обосновано применение закона сохранения импульса
5. Обосновано наличие центростремительного ускорения
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона, формула
центростремительного ускорения, закон сохранения импульса системы);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант,указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) проведены необходимые математические преобразования и расчёты, приводящие к правильному
числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования. Но имеются один или несколько из следующих
недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/ вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
На двух невесомых нерастяжимых вертикальных нитях подвешена горизонтальная пробирка с газом, закрытая пробкой. Масса
пробирки кг, длина нитей
м, нити рвутся, когда к ним прикладывается сила
Н. При нагревании
подвешенной пробирки из неё вылетает пробка массой
со скоростью 10 м/с. Найти минимальную массу пробки,
при которой в момент её вылета нити разорвутся. Обоснуйте применимость законов, используемых для решения
задачи.
Основная волна 2020
Обоснование
1. Введем инерциальную систему отсчёта (ИСО), связанную с землей.
2. Все тела движутся поступательно, поэтому их можно считать материальными точками.
3. Процесс вылета пробки можно считать мгновенным, выполняется закон сохранения импульса.
4. Пробирка движется по окружности, движение будем описывать при помощи второго закона Ньютона. При этом тело обладает
центростремительным ускорением.
Решение
Пусть скорость пробки при вылете равна , а скорость пробирки
. Запишем закон сохранения импульса
где и
– импульсы пробки и пробирки соответственно.
В проекции на горизонтальную ось
После движение пробирки описывается вторым законом Ньютона
где – полное ускорение.
В нижней точке
где - центростремительное ускорение.
Отсюда
Объединим (1) и (2)
Ошибка.
Попробуйте повторить позже
На гладкой горизонтальной плоскости стоит гладкая горка высотой cм и массой
кг, а на ее вершине лежит
небольшая шайба массой
г (см. рисунок). После легкого толчка шайба соскальзывает с горки и движется перпендикулярно
стенке, закрепленной в вертикальном положении на плоскости. С какой скоростью
шайба приближается к стенке по плоскости?
Обоснуйте применимость законов, используемых для решения задачи.
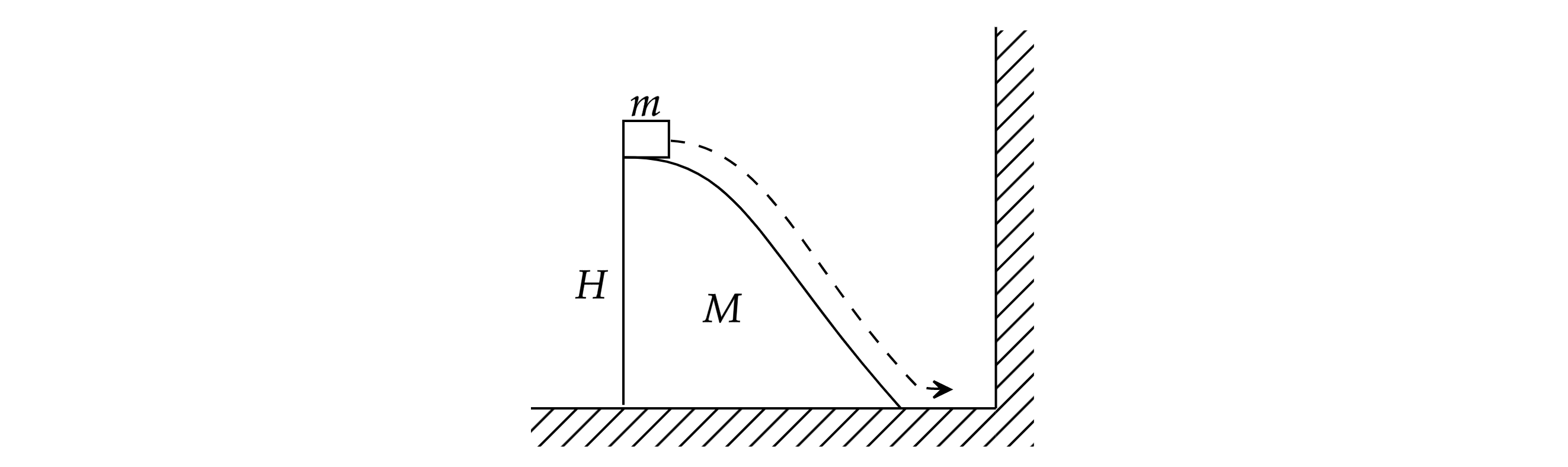
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шайба движется поступательно, будем считать её материальной точкой.
3. Система замкнута, связь между телами идеальная, применимы законы сохранения импульса и энергии.
Решение
Пусть – скорость горки, которая направлена влево,
– скорость шайбы, которая направлена вправо.
Запишем закон сохранения импульса и энергии
Выразим из первого выражения и подставим во второе
Тогда
Ошибка.
Попробуйте повторить позже
К одному концу лёгкой пружины жёсткостью Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости,
другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости
. Груз смещают по
горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и
затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз
движется таким образом, равно
см. Найдите массу
груза. Обоснуйте применимость законов, используемых для решения
задачи.

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его движение можно описывать при помощи второго закона Ньютона, при этом ускорение у тела не постоянно, так как действующие на тело силы меняются с течением времени
3. Для описания движения тела применим закон изменения механической энергии, при этом работа силы нормальной реакции опоры всюда равна нулю, так как она перпендикулярна вектору перемещения.
Решение
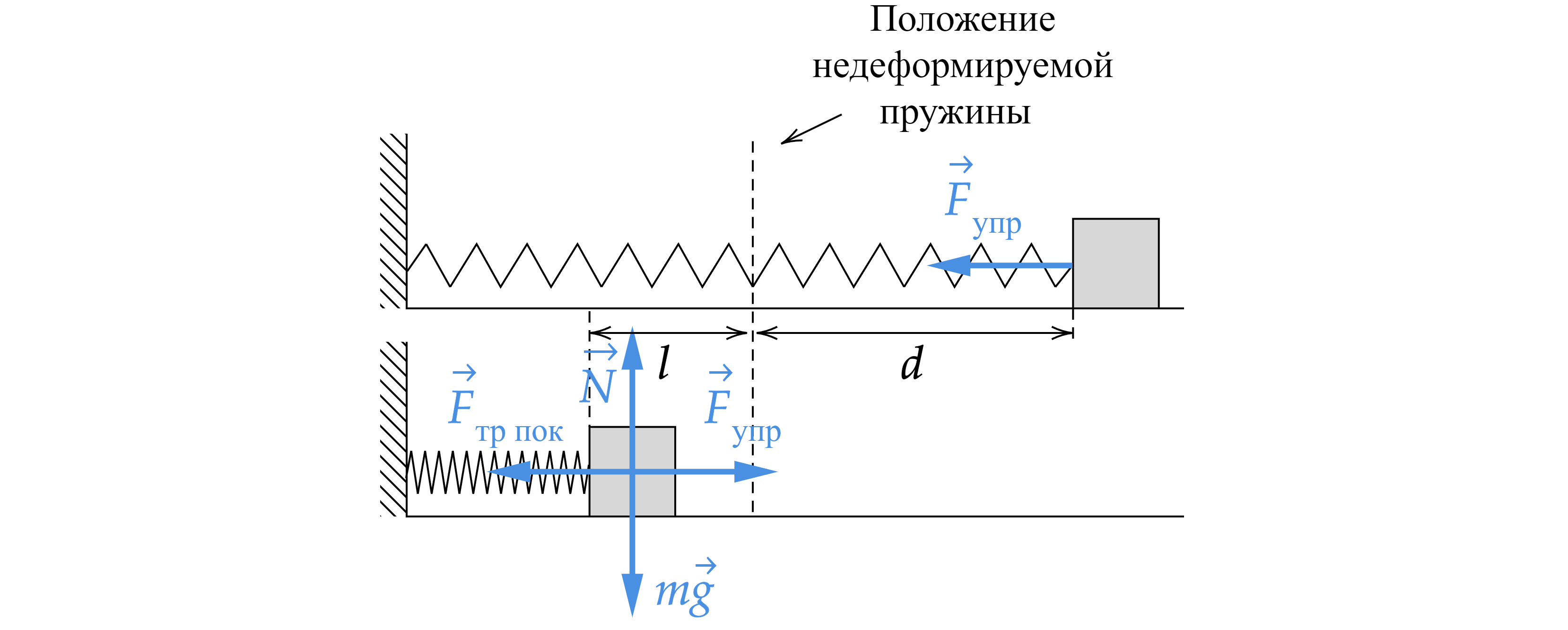
Запишем второй закон Ньютона
в проекции на вертикальную ось
В состоянии покоя
При этом сила трения покоя подчиняется неравенству
Сила упругости по закону Гука равна
Запишем закон об изменении полной механической энергии
Или
При этом и конечная и начальная скорости тела равны нулю, значит конечная кинетическая и начальная кинетическая
энергия
. При этом
, значит,
.
При этом сила трения скольжения равна
Тогда
Отсюда
Для максимального и
Отсюда
Ошибка.
Попробуйте повторить позже
Маленький шарик падает с высоты м над поверхностью Земли из состояния покоя. На высоте
м над землей шарик
испытывает абсолютно упругий удар о закрепленную гладкую площадку, наклоненную под углом
к горизонту (см. рисунок).
Найти дальность полета шарика
.Сопротивлением воздуха пренебречь. Обоснуйте применимость используемых законов к
решению задачи.
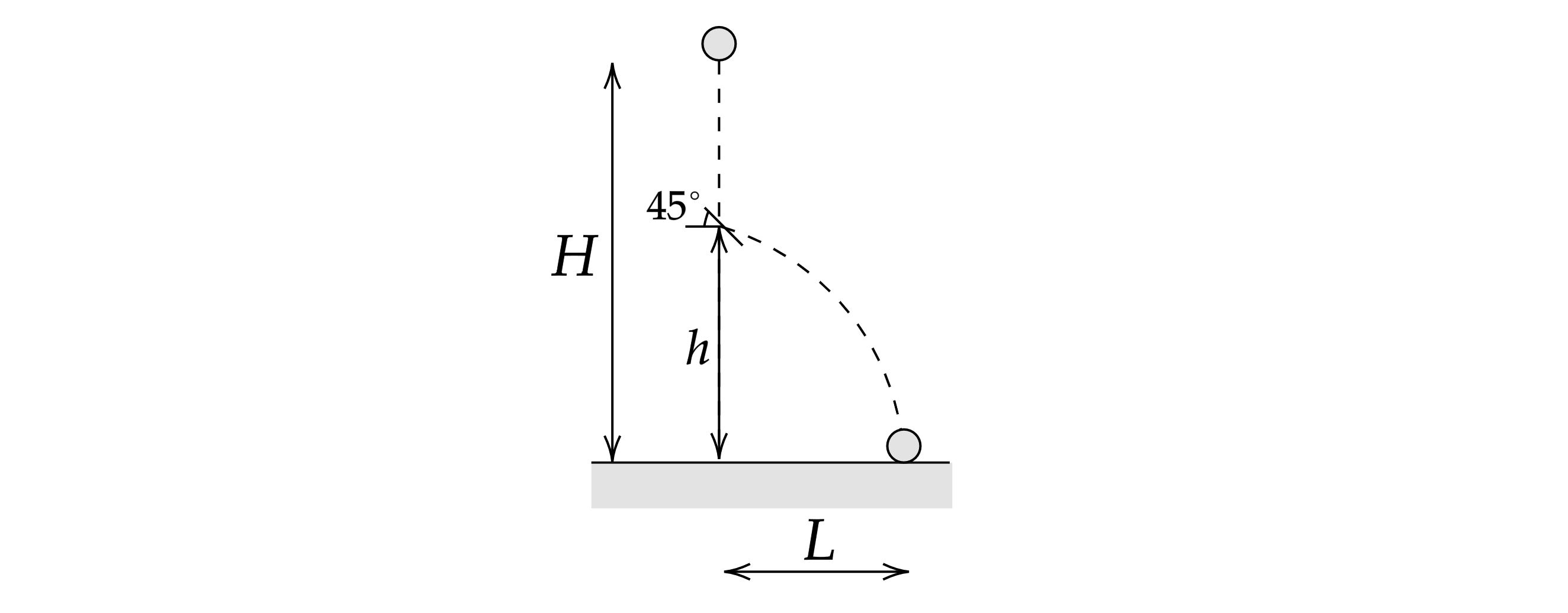
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной
(ИСО).
2. Шарик будем считать материальной точкой.
3. При свободном падении шарика из начального положения на наклонную доску и после удара о доску до падения на землю на шарик действует только потенциальная сила тяжести. Поэтому во введённой нами ИСО при этом движении сохраняется механическая энергия шарика:
При абсолютно упругом ударе шарика о доску механическая энергия шарика сохраняется. Следовательно, сила
трения равна нулю, а направление силы реакции опоры , действующей на шарик при ударе, перпендикулярно
плоскости доски. Отметим, что
, так как время удара коротко, а изменение импульса шарика за время удара
конечно. Поэтому при описании удара пренебрегаем величиной
и записываем второй закон Ньютона для шарика в
виде:
Из того, что следует, что
. Из закона сохранения механической энергии при абсолютно упругом ударе
следует, что
, то есть модуль скорость шарика при таком ударе не меняется. Но точка
, и,
следовательно, угол падения шарика на доску равен углу отражения.
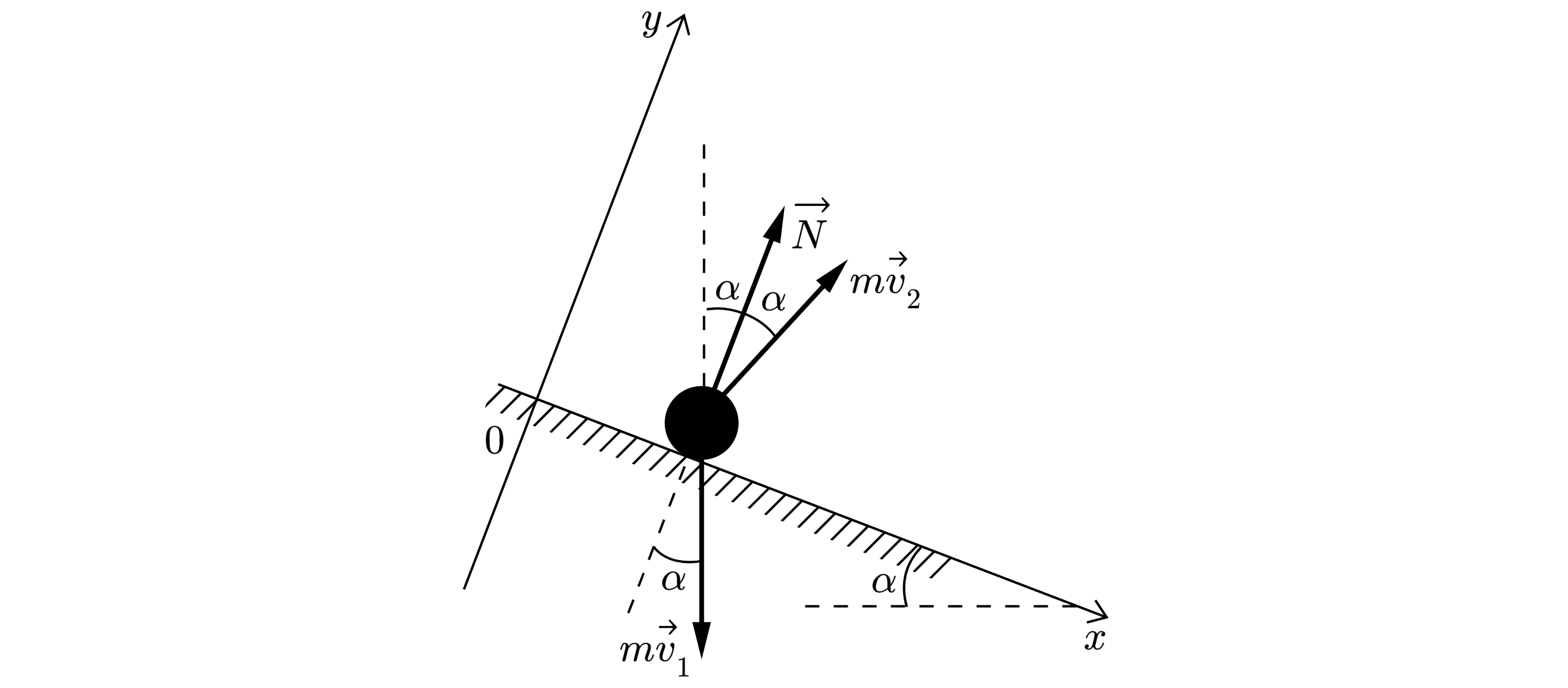
Решение

При падении шарика его потенциальная энергия на высоте преобразуется в кинетическую энергию на высоте
и
потенциальную на высоте
где – масса шарика,
– его скорость на высоте
.
Выразим скорость
Так как , то
и скорость шарика после соударения по вертикали равна
. Значит, шарик будет
иметь только скорость по горизонтали
.
Дальность полёта при равномерном движении
где – время падения с высоты
.
Движение шарика по вертикали описывается уравнением:
Здесь – начальная высота падения,
– начальная скорость тела,
– время движения,
– ускорение свободного
падения.
Следовательно, в момент падения
и окончательный ответ
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение закона сохранения энергии
4. Обосновано равенство скоростей, а также угла падения и отражения
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения энергии, формулы
кинематики равномерного и равноускоренного движения тела).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Пластилиновый шарик в момент бросают с горизонтальной поверхности Земли с начальной скоростью
под углом
к
горизонту. Одновременно с некоторой высоты над поверхностью Земли начинает падать из состояния покоя другой такой же шарик.
Шарики абсолютно неупруго сталкиваются в воздухе. Сразу после столкновения скорость шариков направлена горизонтально. В
какой момент времени
шарики упадут на Землю? Сопротивлением воздуха пренебречь. Какие законы Вы используете для
решения задачи? Обоснуйте их применение.
Обоснование
1) Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли.
2) Шарики будем считать материальными точками, поскольку их размерами в условиях задачи можно пренебречь.
3) Так как сопротивление о воздух не учитывается, то шарики до и после столкновения находятся в свободном падении и
можно использовать формулы кинематики для тела, брошенного под углом к горизонту, и для тела, падающего
вертикально.
4) Для абсолютно неупругого столкновения шариков можно использовать закон сохранения импульса, так как время столкновения
мало и действием внешней силы тяжести за это время можно пренебречь.
Решение
1. Первый шарик начинает движение из начала координат, а второй – из точки А. До столкновения (в точке В) первый шарик
движется по баллистической траектории, а второй шарик свободно падает. Поэтому до столкновения для первого
шарика
а для второго шарика

2. Шарики сталкиваются в момент , при этом импульс системы двух шариков сохраняется:
При этом скорость шариков после удара согласно условию горизонтальна. Поэтому:
, откуда
3. Столкновение шариков происходит на высоте
4. Поскольку скорость шариков после удара горизонтальна, интервал времени от столкновения шариков до их падения на
землю находится из условия:
5. Шарики упадут на Землю в момент
Критерии проверки
Критерий 1
1 балл ставится если
Верно обоснована возможность использования законов (закономерностей). В данном случае: выбор ИСО, материальная точка, условие применения закона сохранения импульса
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса, формулы
кинематики равноускоренного движения);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в
условии задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения физической величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности,
и проведены необходимые преобразования, но имеется один или несколько из следующих
недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол и отпускают. В момент
прохождения шара через положение равновесия в него попадает летящая навстречу пуля, которая пробивает его и продолжает
двигаться горизонтально (см. рисунок). Определите модуль изменения импульса пули в результате попадания в шар, если он,
продолжая движение в прежнем направлении, отклоняется на угол
. (Массу шара считать неизменной; диаметр шара
пренебрежимо малым по сравнению с длиной нити;
.) Сопротивлением воздуха пренебречь. Обоснуйте применимость
законов, используемых для решения задачи.
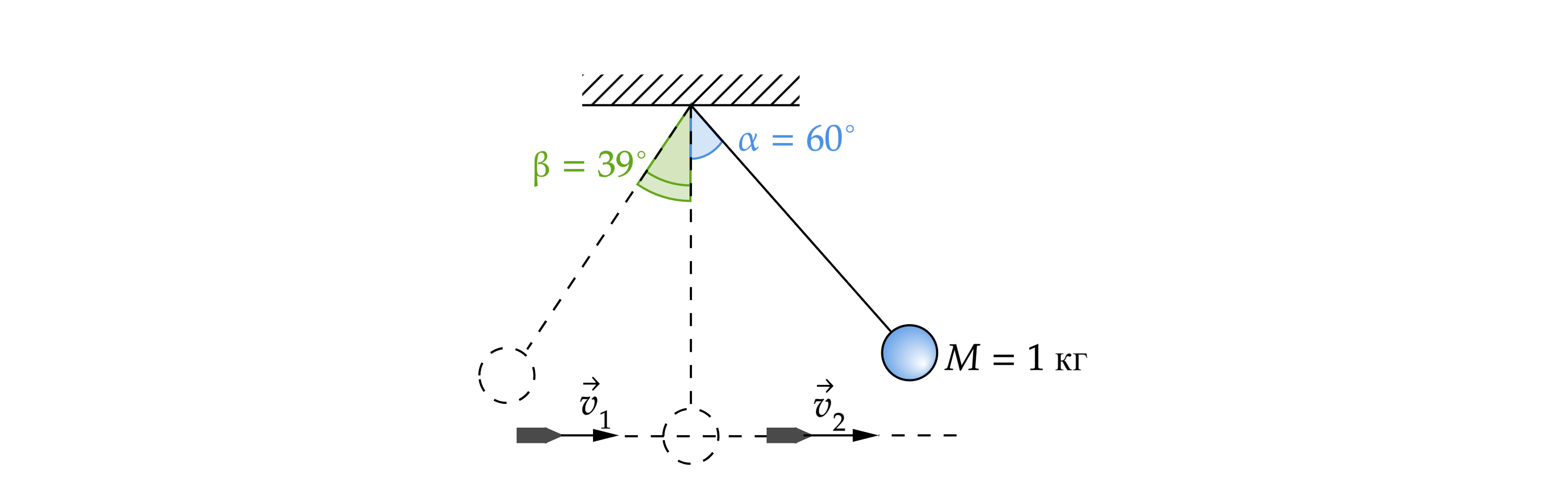
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, размеры шарика малы по сравнению с размерами нити, а пуля еще меньше, поэтому будем описывать шарик и пулю моделью материальной точки.
3. Будем считать, что время соударения шарика и пули мало, а значит нить за это время не успевает заметно отклониться,
поэтому в момент столкновения все силы направлены вертикально. Следовательно, в ИСО при попадании пули в шарик сохраняется
горизонтальная составляющая импульса системы тел "шарик + пуля
".
4. После попадания пули в шарик при движении тел по вертикальной окружности механическая энергия равна сумме кинетической и потенциальной энергии тел. То есть
Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном
случае такой силой является только сила натяжения нити (сопротивлением воздуха пренебрегаем), при этом в любой точке
траектории сила натяжения нити перпендикулярна скорости, поэтому работа силы натяжения нити
равняется
нулю.
5. За нулевой уровень потенциальной энергии примем уровень положения равновесия шара.
Решение
Потенциальная энергия на высоте равна
где – высота подъема,
– масса тела,
– длина нити,
– угол отклонения нити.
Кинетическая энергия в нижней точке
где – скорость шара в нижней точке.
Запишем закон сохранения энергия для движения шарика вниз
Запишем закон сохранения импульс в момент удара и закон сохранения энергии после удара и до подъема на максимальную высоту
|
|
где – высота подъема,
– масса пули,
– скорости шара после столкновения.
Тогда из первого уравнения
Из второго уравнения
Изменение импульса пули
Так как в задаче просят найти модуль изменения импульса, то ответ
Ошибка.
Попробуйте повторить позже
Небольшой груз массой г лежит на горизонтальной опоре. За верёвку, перекинутую через неподвижный блок, его
потянули вверх с постоянной силой
(см. рисунок) из состояния покоя. Через время
с груз оказался на
высоте
м. Какую работу совершила при этом сила натяжения верёвки? Веревку считать нерастяжимой и
невесомой, блок - невесомым. Трение в оси отсутствует. Обоснуйте применимость законов, используемых для решения
задачи.
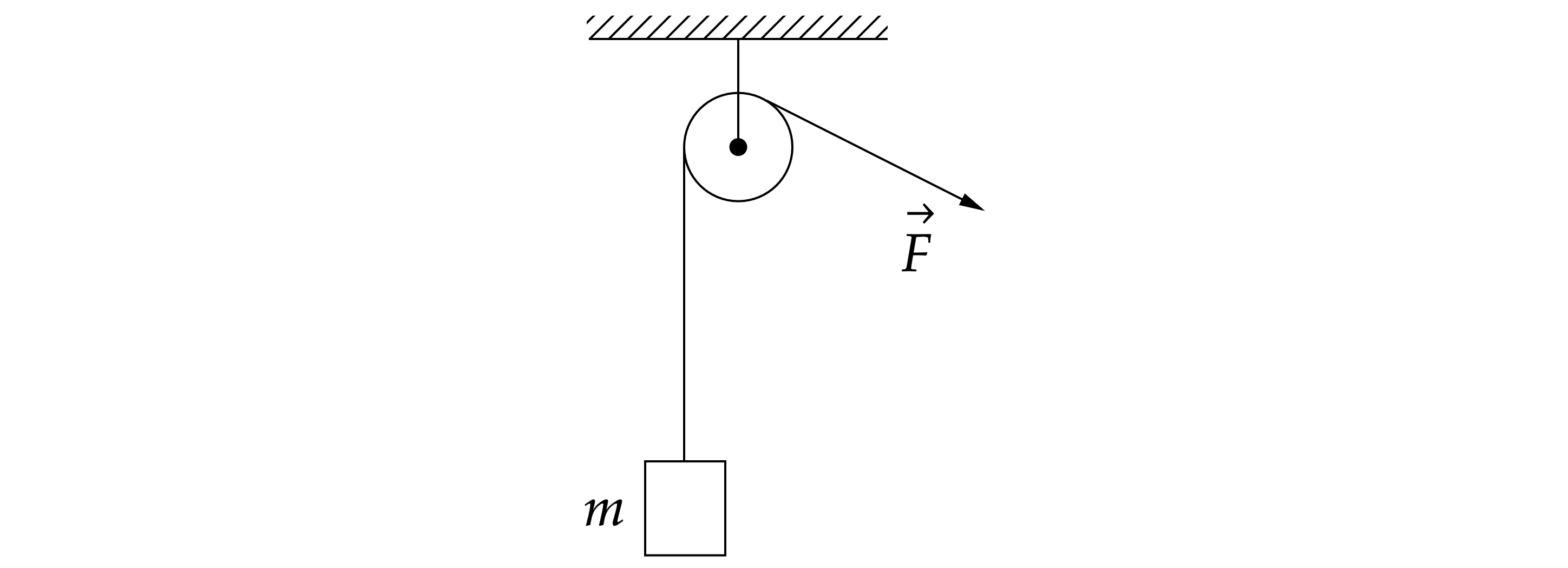
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело будем считать материальной точкой, его поступательное движение в ИСО будем описывать про помощи второго закона Ньютона
Решение
На тело действует сила натяжения и сила тяжести
.
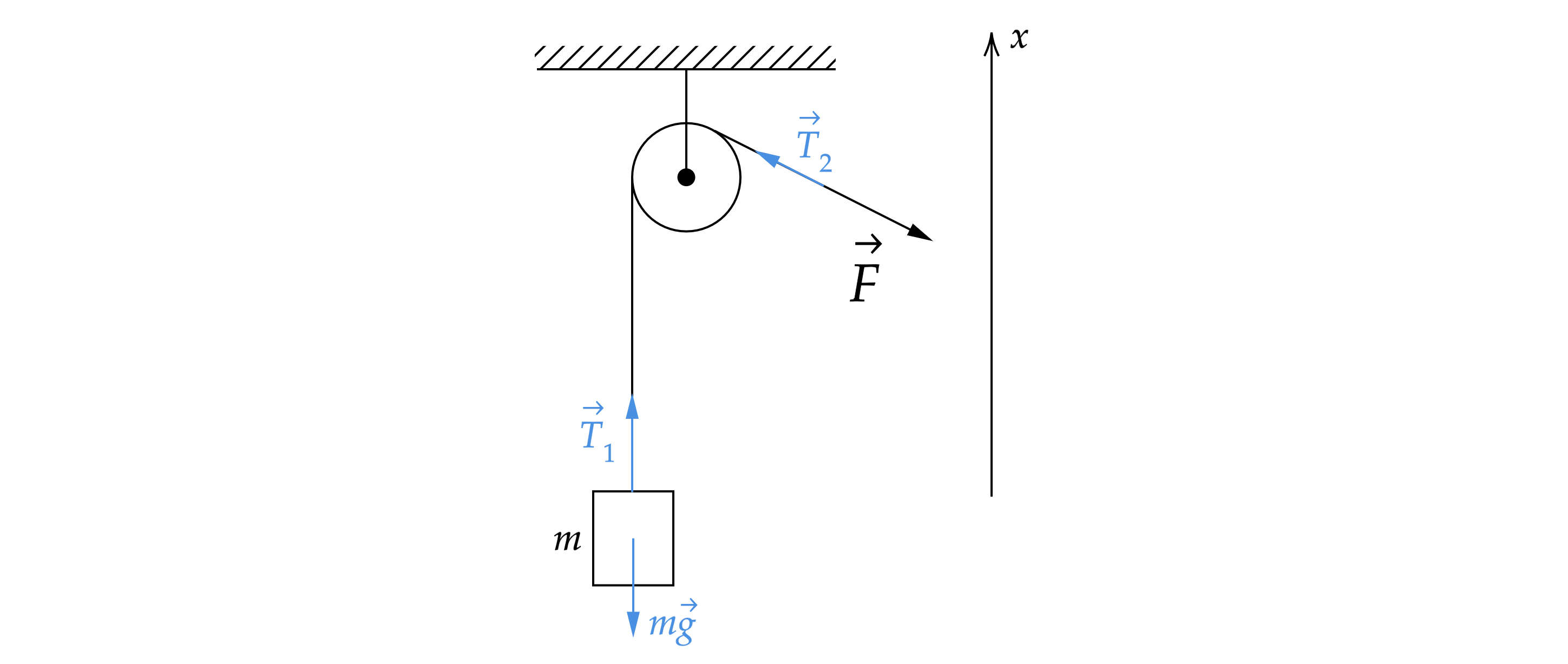
Запишем второй закон Ньютона
где – ускорение тела.
В проекции на вертикальную ось :
Ускорение можно найти из уравнения кинематики
где – начальная скорость.
Работа силы натяжения нити
где – угол между силой и перемещением.
Объединяя (1) – (3), получим
Критерии проверки
Критерий 1
1 балл ставится если
Верно обоснована возможность использования законов (закономерностей). В данном случае: выбор ИСО, материальная точка, применение второго закона Ньютона
_________________________________________________________________________________________________________________________
В обосновании отсутствует один или несколько из элементов.
(ИЛИ)
В обосновании допущена ошибка.
(ИЛИ)
Обоснование отсутствует
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона, формулы
кинематики равноускоренного движения, работы силы натяжения нити);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых вусловии
задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения физической величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования, но имеется один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
B необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения
и формулы, выражающие физические законы, применение которых необходимо для решения данной
задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Маленький шарик массой подвешен на лёгкой нерастяжимой нити длиной
которая разрывается
при некоторой силе натяжения
Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и
отпущен. Когда шарик проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго
сталкивается с бруском массой
лежащим неподвижно на гладкой горизонтальной поверхности стола.
Скорость бруска после удара
Определите величину силы
Считать, что брусок после удара движется
поступательно.
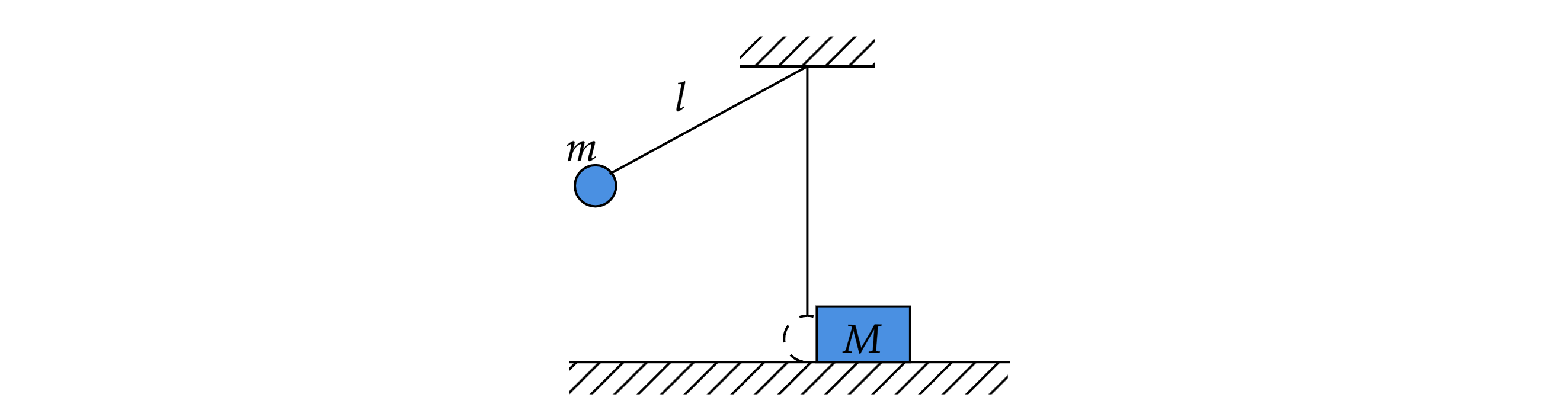
Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью материальной точки.
3. Будем считать, что время соударения мало, и действие внешних сил во много раз меньше сил внутренних, поэтому момент соударения будем описывать с использованием закона сохранения импульса.
4. Поскольку шар является материальной точкой, его движение в ИСО будем описывать при помощи второго закона Ньютона.
5. Поскольку шар движется по дуге окружности радиуса , он будет обладать центростремительным ускорением, направленым
к центру окружности.
Решение
Запишем второй закон Ньютона в момент, когда шарик касается бруска.
где - полное ускорение.
В проекции на вертикальную ось, направленную вверх
где – сила тяжести,
– центростремительное ускорение,
– скорость шарика.
Распишем все составляющие закона по формулам и получим:
– скорость перед столкновением с бруском. Также запишем закон сохранения импульса при абсолютно неупругом
ударе
где – импульс шарика,
– импульс бруска,
– импульс бруска и шарика после удара. Распишем все составляющие по
формулам, с учетом того, что брусок покоится
Выразим скорость перед столкновением:
Подставим выраженную скорость в закон, который мы расписали выше:
Ошибка.
Попробуйте повторить позже
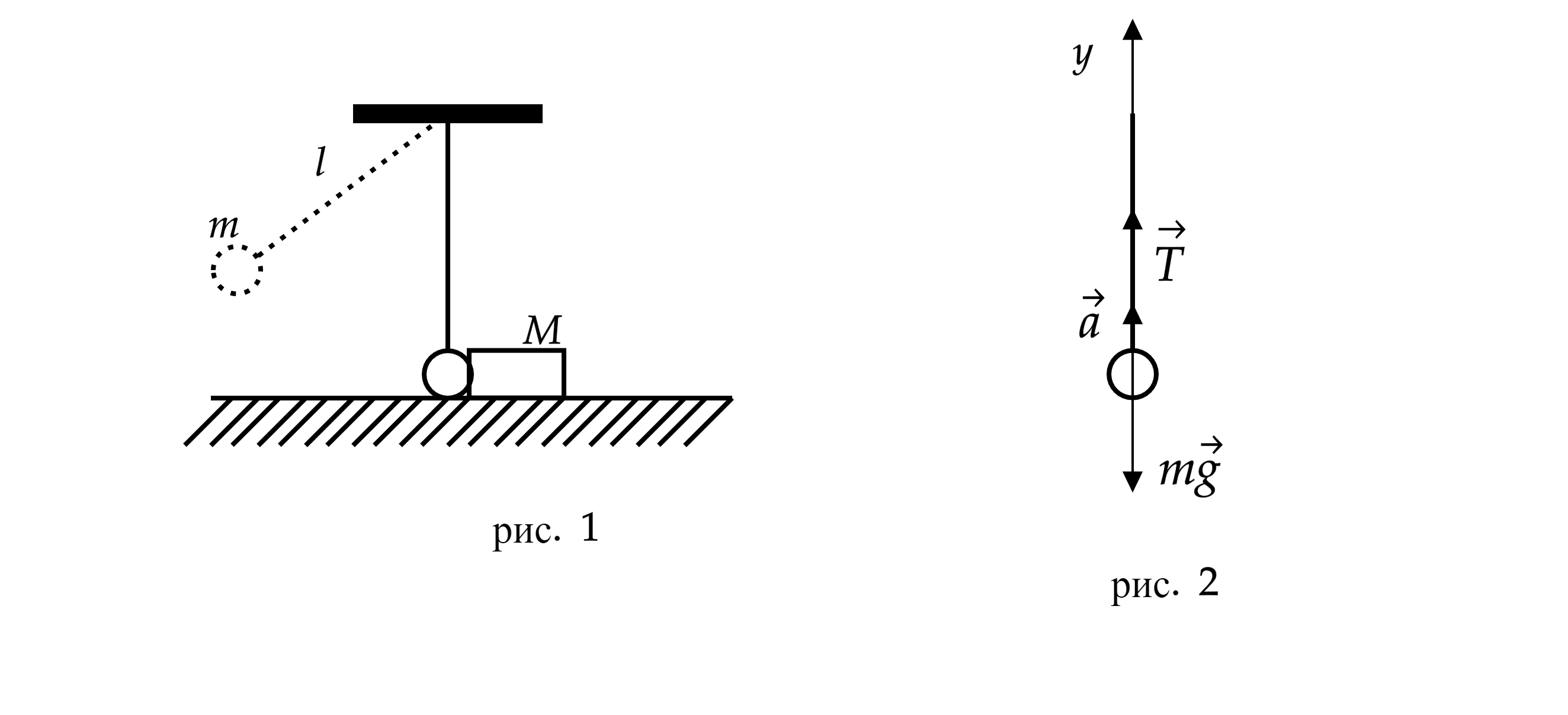
Маленький шарик массой подвешен на лёгкой нерастяжимой нити длиной
которая разрывается
при силе натяжения
Шарик отведён от положения равновесия (оно показано на рисунке пунктиром) и
отпущен. Когда шарик проходит положение равновесия, нить обрывается, и шарик тут же абсолютно неупруго
сталкивается с бруском, лежащим неподвижно на гладкой горизонтальной поверхности стола. Скорость бруска после
удара
Какова масса
бруска? Считать, что брусок после удара движется поступательно.
Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.
Источники:
1. Непосредственно перед обрывом нити в момент прохождения положения равновесия шарик движется по окружности радиусом
со скоростью
. В этот момент действующие на шарик сила тяжести
и сила натяжения нити
направлены по вертикали и
вызывают центростремительное ускорение шарика. Запишем второй закон Ньютона в проекциях на ось
инерциальной системы
отсчёта
, связанной с Землёй:
2. При прохождении положения равновесия нить обрывается, и шарик, движущийся горизонтально со скоростью , абсолютно
неупруго сталкивается с покоящимся бруском. При столкновении сохраняется импульс системы «шарик + брусок». В проекциях на
ось
получаем:
где — проекция скорости бруска с шариком после удара на ось
Отсюда:
Выразим искомую массу:
Ошибка.
Попробуйте повторить позже
По гладкой наклонной плоскости, составляющей угол с горизонтом, скользит из состояния покоя брусок массой
В тот момент, когда брусок прошёл по наклонной плоскости расстояние
в него попала и застряла в нём
летящая навстречу ему вдоль наклонной плоскости пуля массой
После попадания пули брусок поднялся вверх вдоль
наклонной плоскости на расстояние
от места удара. Найдите скорость пули перед попаданием в брусок. Трение бруска о
плоскость не учитывать.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Брусок движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать брусок моделью материальной точки.
3. Процесс попадания пули мгновенный, значит, действием внешних сил можно пренебречь, можно применить закон сохранения импульса. Так как размеры пули меньше размера бруска, то ее также можно описывать моделью материальной точки.
Решение
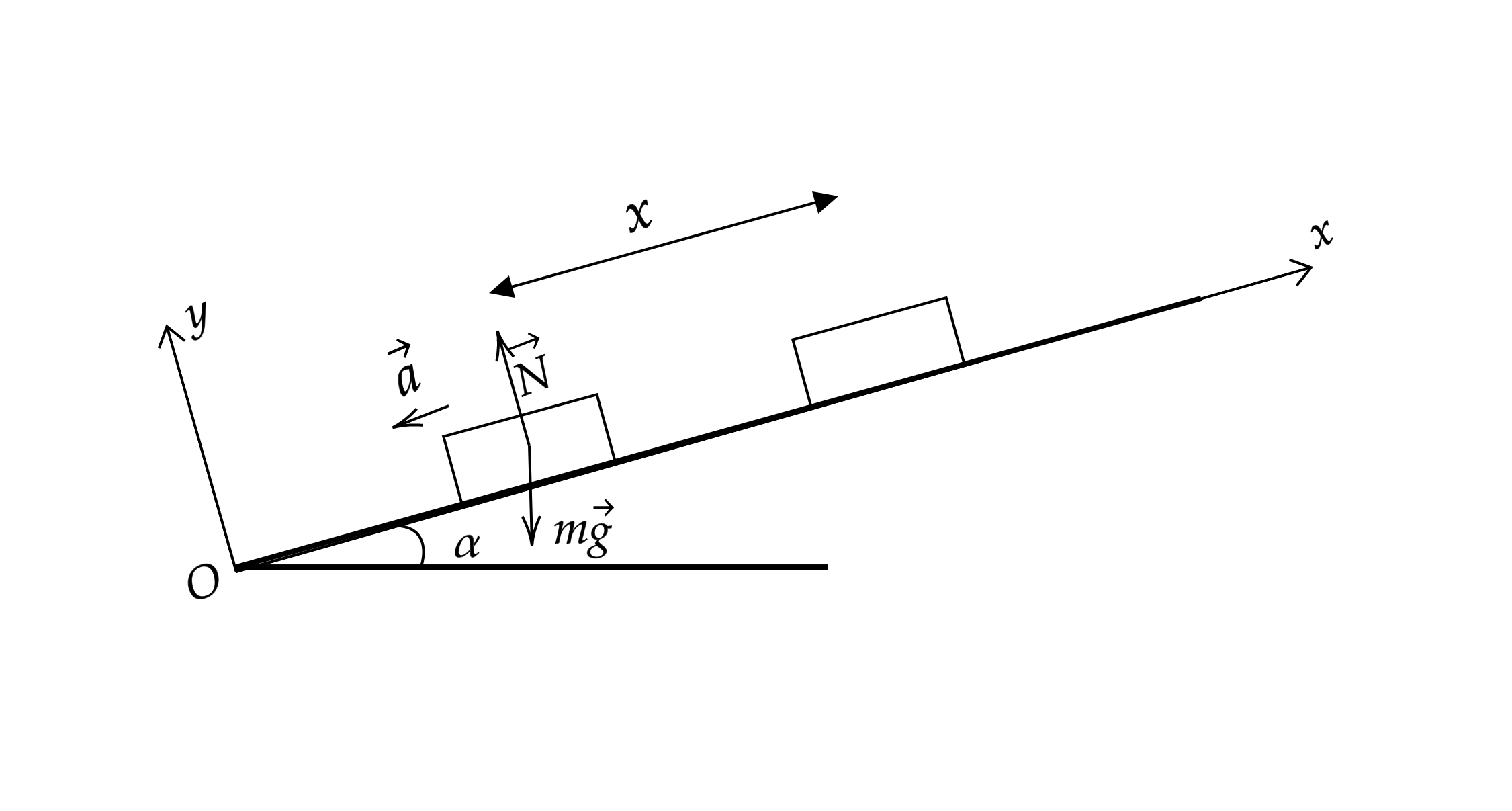
Запишем второй закон Ньютона
Здесь – сила реакции опоры,
– ускорение тела.
Спроецируем второй закон Ньютона на ось
Тело будет двигаться по наклонной поверхности с ускорением . У нас имеется формула расстояния
где и
– конечная и начальная скорости тела,
– ускорение тела.
В нашем случае тело двигается из состояния покоя, то есть
Отсюда конечная скорость равна
Воспользуемся законом сохранения импульса
Или в проекции на ось, совпадающую с движением тела
где – скорость составного тела сразу после попадания пули.
Дальше воспользуемся первоначальным уравнением расстояния, с учетом того, что ускорение , а конечная скорость
равна 0
Выразим
Подставим (1) и (2) в закон сохранения импульса:
Выразим нужную нам скорость:
Ошибка.
Попробуйте повторить позже
Небольшой кубик массой начинает скользить с высоты
с нулевой начальной скоростью по
гладкой горке, переходящей в «мёртвую петлю» радиусом
(см. рисунок). На какой высоте h от нижней
точки петли сила давления кубика на стейку петли
Сделайте рисунок с указанием сил, поясняющий
решение. Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.
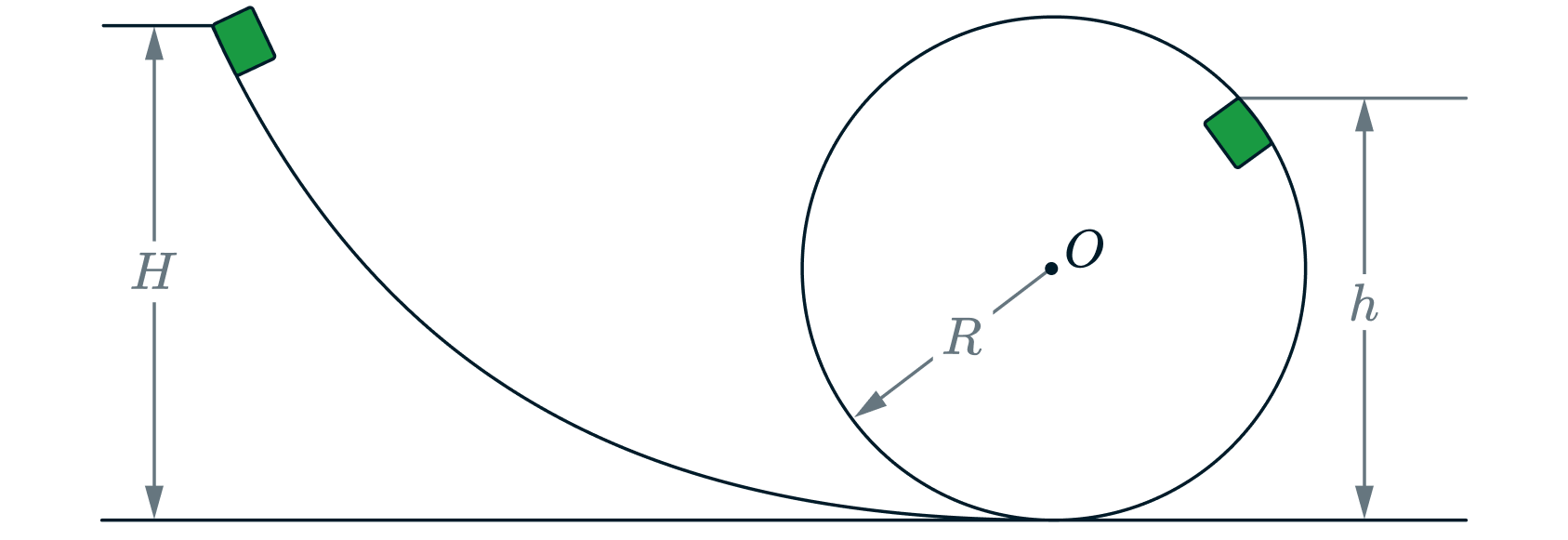
Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Кубик движется поступательно и имеет малые размеры по сравнению с мёртвой петлёй, поэтому его можно считать материальной точкой.
3. Так как груз является материальной точкой, то описывать его движение в ИСО будем, используя законы Ньютона.
4. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в
данном случае такой силой является только сила реакции опоры , (сопротивлением воздуха пренебрегаем, трения нет,
поверхность гладкая), при этом в любой точке траектории сила реакции опоры перпендикулярна скорости, поэтому работа этой
силы равняется нулю и полная механическая энергия кубика при его движении сохраняется.
5. При движении по окружности тело будет обладать центростремительным ускорением, направленным к центру окружности вращения.
Решение
Запишем закон сохранения энергии
где – скорость бруска на высоте

По рисунку найдем , он равен:
Сделаем рисунок, с расставлением всех сил, действующих на брусок на высоте .
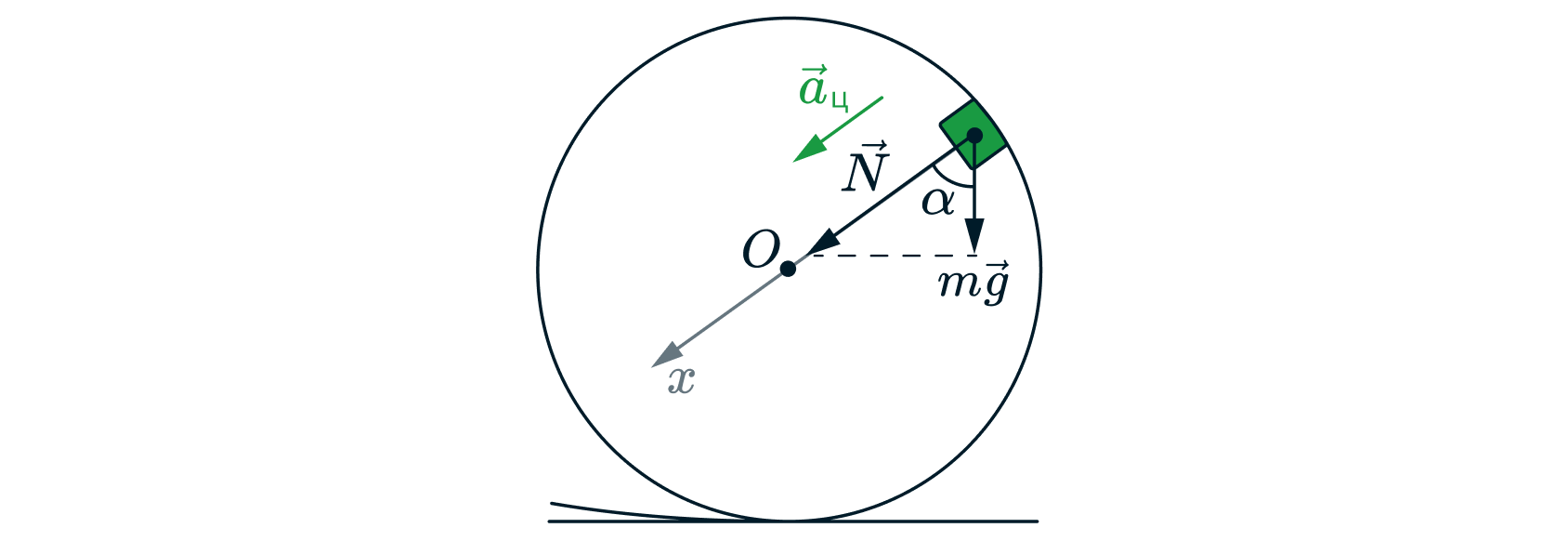
Запишем второй закон Ньютона в проекции на ось
где – центростремительное ускорение.
По третьему закону Ньютона значит, скорость кубика на высоте
равна
Подставив значение скорости в закон сохранения энергии, и выразив высоту получим



