Тема Векторы и координаты в планиметрии

Введение векторов или координат в планиметрии

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела векторы и координаты в планиметрии

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#76173

Дед Мороз наколдовал на серединах сторон треугольника $ABC$ шестиконечные снежинки, как показано на рисунке:

$PIC$

(вершина треугольника и середина стороны треугольника берутся концами стороны соответствующего правильного шестиугольника)

Докажите, что на полученном новогоднем чуде точки пересечения медиан треугольников $ABC$ и $XY Z$ совпадают.

Показать доказательство

Пусть $O$ — произвольная точка плоскости.

Про точку $M$ пересечения медиан треугольника $ABC$ известно, что:

−−→ −→ −−→ −−→ 3OM = OA +OB + OC

(это характеристическое свойство следует из того, что точка пересечения медиан является центром масс $−M−A→ +−M−B→ +−M−C→ = −→0$ )

А требуется доказать, что $M$ является ещё и точкой пересечения медиан треугольника $XY Z$ , то есть:

−−→ −−→ −−→ −→ 3OM = OX +OY + OZ

Левые части полученных двух векторных равенств совпадают, поэтому надо доказать про правые, что разность правых частей в этих равенствах равна нулевому вектору, то есть (преобразуем по правилу вычитания векторов):

−−A→X +−B→Z + −−C→Y = −→0

Возьмём серединный треугольник $A0B0C0$ и повернём его вокруг точки $M$ на $60∘$ . Получим треугольник $A1B1C1$ такой, что

A1B1 ∥ AX, B1C1 ∥BZ, C1A1 ∥CY

К тому же,

A1B1 =A0B0 = AB∕2= AX,B1C1 =B0C0 =BC ∕2= BZ,C1A1 = C0A0 = CA∕2 =CY

Значит,

−−→ −−−→ −→ −−−→ −−→ −−−→ AX = B1A1,BZ = B1C1,CY =C1A1

Но тогда получаем требуемое:

−−A→X +−B→Z + −−C→Y = −−B−1→A1+ −−B−1→C1+ −−C−1A→1 = −→0

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#85562

По плоскости ползут три улитки. Каждая улитка движется со своей скоростью прямолинейно и равномерно. Известно, что в некоторые три момента времени все улитки оказывались на одной прямой. Могут ли улитки в какой-то момент времени оказаться в вершинах правильного треугольника?

Источники: Курчатов - 2024, 11.4 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Как в геометрии, так и в других разделах математики, зачастую бывает удобно зафиксировать задачу набором переменных. Если мы хотим зафиксировать задачу здесь, то самым банальным набором будет функция движения каждой улитки. Пусть (x_i(t), y_i(t)) - положение улитки относительно времени. Какое тогда условие, при наличии направляющих векторов можно наложить на их координаты, если в некоторый момент времени эти три улитки были

Подсказка 2

Верно, что (x_2(t) - x_1(t))(y_3(t) - y_1(t)) = (x_3(t) - x_1(t))(y_2(t) - y_1(t)). Просто записали векторное произведение векторов от первой ко второй улитке и от первой к третьей. Что теперь можно понять, если у нас нашлось 3 значения таких t(то есть, три раза был момент, когда они все на 1 прямой)? А если подумать какой степени каждая из зависимостей x_i, y_i относительно t?

Подсказка 3

Зависимости x_i, y_i - линейный зависимости(так как каждая улитка движется по линии), а значит, уравнение выше - не выше второй степени. Однако, у него есть три различных корня. Что это значит тогда? Когда такое может быть?

Показать ответ и решение

Введем декартову систему координат, и пусть $(x (t);y(t)),i= 1,2,3 i i$ - координаты $i$ -й улитки в момент времени $t$ . Поскольку улитки движутся прямолинейно и равномерно, то $xi(t)$ и $yi(t)$ - линейные функции от времени $t$ . Рассмотрим векторы

¯a(t)= (x (t)− x(t);y (t)− y (t)), 2 1 2 1 ¯b(t)=(x3(t)− x1(t);y3(t)− y1(t)),

направленные от первой улитки ко второй и третьей соответственно. Тогда условие принадлежности трех улиток одной прямой равносильно коллинеарности векторов $¯a(t)$ и $¯ b(t)$ .

Это в свою очередь равносильно пропорциональности координат этих векторов:

(x2(t)− x1(t))(y3(t)− y1(t))= (x3(t)− x1(t))(y2(t)− y1(t)).

Заметим, что это равенство представляет собой уравнение на переменную $t$ степени не выше 2. Нам известно, что у этого уравнения есть три различных корня. Но тогда это уравнение имеет тривиальный вид $0 =0$ , поскольку в противном случае у него не может быть больше двух корней. Значит, это уравнение справедливо при любом $t$ , и улитки всегда находятся на одной прямой и не могут оказаться в вершинах ни одного треугольника.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 3#87529

На каждой из двух прямолинейных линий электропередач установлены обслуживающие подстанции. На линии А — через каждые $m$ км, на линии В — через каждые $q$ км. Если занумеровать их подряд вдоль каждой линии, то расстояния между подстанциями $A1$ и $B1$ равно $√- 15 2$ км, между $A3$ и $B3$ равно $√-- 5 34$ км, между $A4$ и $B4$ равно $√-- 15 10$ км. Определите, параллельны ли данные линии? Если да, то найдите расстояние между ними. Если нет, то найдите расстояние от подстанции $A1$ до точки их пересечения.

Источники: Надежда энергетики - 2024, 11.2 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Как можно записать условие более ёмко? Можно ввести координаты.

Подсказка 2

Мы можем составить уравнение квадрата расстояния от Aₙ до Bₙ. Как оно может выглядеть?

Подсказка 3

Координаты подстанций будут линейно изменяться. Тогда расстояние можно представить как многочлен второй степени.

Подсказка 4

У нас есть 3 уравнения и 3 неизвестных, можем найти все коэффициенты многочлена. Как понять, будут ли линии пересекаться?

Подсказка 5

Значение многочлена всегда больше 0, так как дискриминант меньше 0. Тогда линии параллельны, а квадрат расстояния между ними равен минимальному значению многочлена. Его можно найти через вершину.

Показать ответ и решение

Если ввести декартову систему координат с началом в точке $A 1$ и одной из осей, направленной вдоль линии $A$ (можно и иначе), то координаты всех подстанций будут изменяться линейным образом, следовательно, квадраты расстояний $AkBk$ будут являться значениями некоторого многочлена второй степени $2 P(s)= as + bs+ c$ . Найдём его. Будем измерять $s$ в условных единицах длины, так что каждая следующая единица соответствует следующей паре подстанций. Тогда

2 P (0)= c= A1B1 = 9⋅50

2 P (2)= 4a+ 2b+ c= A3B3 = 17⋅50

2 P (3)= 9a+ 3b+ c= A4B4 = 45⋅50

Для простоты расчетов уменьшим все правые части в $50$ раз и из полученной линейной системы найдём

a= 8,b =− 12,c= 9.

Следовательно, искомый многочлен имеет вид

P(s)= 50(8s2− 12s+ 9)

Его дискриминант отрицателен, $P(s)$ нигде не обращается в ноль (и всюду положителен). Следовательно, линии не пересекаются. Квадрат расстояния между ними равен минимальному значению $P (s)$ , которое достигается при $s =s0 = 34$ и равно $50⋅ 92 = 225$ . А само расстояние равно 15.

Ответ:

Линии параллельны, расстояние между ними равно $15$ км.

Ошибка.
Попробуйте повторить позже

Задача 4#67114

В треугольнике $ABC$ точка $O$ — центр описанной окружности, точка $H$ — ортоцентр. Отрезки $OA,OB$ и $OC$ параллельно перенесли и последовательно приставили друг другу. Получилась ломаная. Докажите, что отрезок, соединяющий концы ломаной, равен и параллелен $OH.$

Подсказки к задаче

Подсказка 1

Отрезки, которые друг от друга откладывают, и нам важно только расстояние между началом и концом… Да это же задача на векторы! То есть нас просят доказать векторное равенство OH=OA+OB+OC (всё в векторах). Сразу такое доказывать страшно и не понятно как. Может быть преобразовать два каких-то слагаемых из этой суммы, с помощью дополнительного построения?

Подсказка 2

Если у нас есть ортоцентр, то надо пользоваться его свойством. При этом таким свойством, чтобы где-то обнаружить отрезок BH, потому что в данный момент совершенно неясно, что с ним делать, а только с ним что-то делать и остается, так как оба отрезка: OH и OB, как-то с ним связаны. Так какое доп. построение здесь может зарешать?

Подсказка 3

Оп-па, можно отразить точку О относительно AC (пусть образ точки O- это О₁). Тогда OO₁=HB, по свойству ортоцентра, при этом, очевидно, HBOO₁ — параллелограмм. А значит, OH можно легко выразить через OB и OO₁. Осталось выразить, в силу того, что СOAO₁ — параллелограмм, сумму векторов OA+OC, после чего увидеть, что задача решена!

Показать доказательство

Иными словами, нас просят доказать векторное равенство

−−→ −→ −−→ −−→ OH =OA + OB + OC(Формула-Гамильтона)

$PIC$

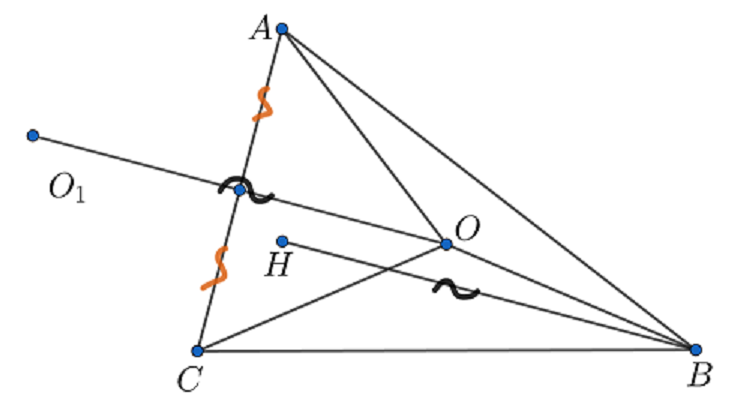
Пусть $O1$ симметрична $O$ относительно середины $AC,$ тогда

−O→A +−O−→C = −O−O→1.

По свойству ортоцентра $BH = OO1$ и $BH ∥ OO1,$ значит $HBOO1$ — параллелограмм, следовательно,

−−→ −−→ −−→ OB + OO1 = OH

Таким образом,

−→ −−→ −−→ −−→ OA + OB +OC = OH

Ошибка.
Попробуйте повторить позже

Задача 5#68554

Из медиан треугольника $ABC$ составлен треугольник $A B C , 1 1 1$ а из медиан треугольника $A B C 1 1 1$ составлен треугольник $A B C . 2 2 2$ Докажите, что треугольники $ABC$ и $A2B2C2$ подобны, и найдите коэффициент подобия.

Подсказки к задаче

Подсказка 1

Для начала надо построить треугольник A₁B₁C₁. Вы же помните, как выражается вектор медианы через вектора сторон?

Подсказка 2

Если проведена медиана AM₁, то вектор AM₁ равен полусумме векторов AB и AС. Нетрудно увидеть, что сумма векторов AM₁, BN₁ и CK₁ равна 0 (BN₁ и CK₁- векторы оставшихся медиан), а значит из них действительно можно сложить треугольник. Может тогда посмотрим, как выражаются медианы треугольника A₁B₁C₁?

Подсказка 3

Мы знаем, что для векторов нашего треугольника A₁B₁C₁ верны следующие равенства: A₁B₁= AM₁, B₁C₁=BN₁, C₁A₁=CK₁. Тогда вектор медианы A₁M₂ равен полусумме векторов AM₁ и K₁C. Как тогда можно выразить вектор A₁M₂ через вектора треугольника ABC?

Подсказка 4

A₁M₂=(AM₁+M₁C)/2=(AB+AC+BC+AC)/4=3*AC/4. Осталось аналогично выразить остальные векторы медиан B₁N₂ и C₁K₂ и завершить решение!

Показать ответ и решение

Первое решение.

Пусть медианы $△ABC$ будут $′ AA ,...$ и аналогично для $△A1B1C1$ ( $′′ A1A ,...$ ). Тогда из $△ABC$ имеем

−→ −→ −→ −−→ −−→ −→ −A−→A ′ =AB-+-AC , −B−B→′ = BA+-BC-, −C−C→′ = CB+-CA 2 2 2

Заметим, что сумма всех векторов равна нулю, поэтому из них можно составить треугольник. Это важно, поскольку тогда мы можем использовать их в качестве сторон $A1B1C1$ ( $−A−→A′ → −A−1−B→1,−B−B→′ → −B−−1→C1,−C−C→′ → −C−1−→A1$ ). Далее из треугольника $△A1B1C1$ получим

−−−→ −−−→ −−−→ −→ −→ −−→ −→ −→ A1A′′= A1B1-+A1C1 = AB-+AC-+-BC-+AC- = 3AC-- 2 4 4

Здесь мы воспользовались тем, что $−A→B + −−B→C +−C→A = −→0 .$ Повторяя аналогичные рассуждения для остальных сторон, получаем подобие с коэффициентом $34.$

Второе решение.

Если стороны треугольника равны $a,b,c,$ то квадраты длин медиан выражаются по формулам

m2 = 2b2+-2c2-− a2 a 4

2 2c2+-2a2− b2 mb = 4

2 2a2+ 2b2− c2 mc = ----4------

Тогда у треугольника $A2B2C2$ квадраты длин сторон, как медианы треугольника $A1B1C1,$ выражаются по формулам

2 2 2 2m-b +2m-c − m-a= 4

= -1⋅(2(2b2+ 2c2− a2)+2(2c2+ 2a2− b2)− (2a2+ 2b2− c2)) 16

-1 ( 2) ( 3c)2 = 16 ⋅9c = 4

Далее аналогично считаются длины оставшихся двух сторон. В итоге у треугольника $A2B2C2$ стороны равны $34c,34b,34a,$ поэтому он подобен исходному треугольнику со сторонами $a,b,c,$ коэффициент подобия равен $3. 4$

Ответ:

$3 4$

Ошибка.
Попробуйте повторить позже

Задача 6#45004

На стороне $AB$ и диагонали $AC$ квадрата $ABCD$ отмечены точки $M$ и $N$ соответственно так, что $AM :MB = 1:4,AN :NC = 3:2.$

а) Докажите, что точки $A,M,N,D$ лежат на одной окружности.

б) Найдите расстояние от точки пересечения диагоналей четырёхугольника $AMND$ до прямой $MN$ , если сторона квадрата равна $45.$

Показать ответ и решение

Первое решение.

$PIC$

а) Так как по условию $AM = 15AB,$ то

tg∠AMD = 5

По условию $AN = 35AC.$ Отметим точку $O$ — центр квадрата. Тогда $AO = 12AC = OD.$ Поэтому

1 tg ∠AND = 3-21-= 6-1- =5 5 −2 5 − 1

В силу того, что углы от 0 до 180 градусов невключительно, из $tg∠AMD =tg∠AND$ следует $∠AMD = ∠AND,$ дающее вписанность.

б) Пусть точка $S$ — точка пересечения $AM$ и $ND$ . Из вписанности имеем $∠ANM =∠ADM,$ так что искомое расстояние

AM SH = SN sin∠ANM =SN sin∠ADM = (AN − AS )⋅MD-

Из подобия треугольников $AMS$ и $SCD$

1 √ - AS :SC = AM :CD = 1:5 =⇒ AS = 6AC = 7,5 2

Из условия задачи

3 √- AN = 5AC = 27 2

∘------ √ -- AM = 15AB = 9,MD = 92+ 452 =9 26

В итоге получаем

√ -- SH = 19,5√2-√1-= -3√9- = 3-13 26 2 13 2

Второе решение.

$PIC$

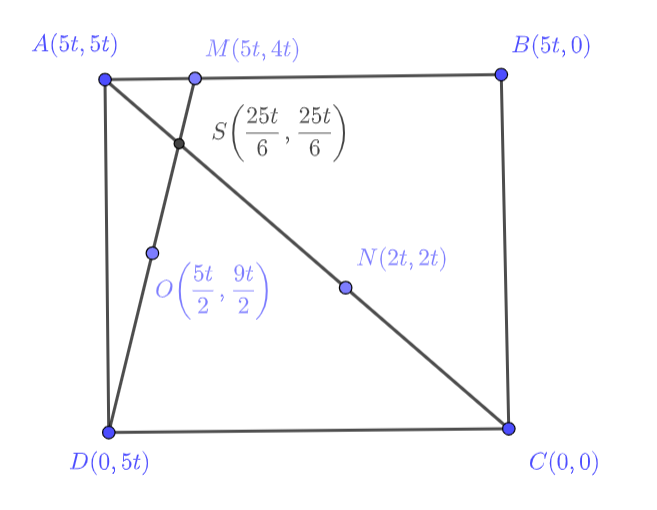
a) Заметим, что если ввести систему координат с центром в точке $C$ , а ось $x$ пустить по лучу $CB$ , ось $y$ - по $CD$ , а $|CD|= 5t$ , то мы легко найдем координаты всех точек, что нам даны. Тогда мы можем найти центр описанной окружности $O$ прямоугольного треугольника $AMD$ - середину гипотенузы, тогда $O (5t2 ;92t )$ . Находим расстояние между точками $O,N$ , равное $∘ ----------------- (5t2-− 2t)2+ (92t− 2t)2$ , и убеждаемся, что оно равно $12|AM |= 12∘(5t)2+-t2$ , то есть $A,M,N,D$ действительно лежат на одной окружности.

б) В нашей системе координат прямая $ND$ задаётся уравнением $x= y$ , а прямая $AM$ : $y = 5t− x5$ , откуда сразу находим, что точка $S$ пересечения $AM$ и $ND$ имеет координаты $S(25t,25t) 6 6$ . Так как прямая $NM$ задаётся (по двум точкам) уравнением: $2x− 3y+ 2t =0$ , вспоминаем формулу расстояния от точки до прямой и записываем ответ, подставляя $5t= 45 =⇒ t= 9 =⇒$

|2 ⋅ 25t− 325t+ 2t| 3√13- ρ(S,NM )= ---6√22+632----= --2-

Ответ:

$3√13 2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#72976

В выпуклом 12-угольнике все углы равны. Известно, что длины каких-то десяти его сторон равны 1, а длина ещё одной равна 2. Чему может быть равна площадь этого 12-угольника?

Источники: ММО-2022, 11.3 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть длины сторон это 10 единиц, 2 и x. Очень хочется найти x... Попробуем рассмотреть векторы, соответствующие сторонам и поработать с ними.

Подсказка 2

Т.к. мы всё-таки хотим использовать длины сторон, то работать будем не с самими векторами, а с коллинеарными им единичными. Т.к. мы знаем, что они образуют многоугольник, то мы можем записать уравнение на них. А как быть с равными углами? Что можно сказать о взаимно расположении некоторых единичных векторов?

Подсказка 3

Заметим, что каждый угол равен 150. Тогда мы можем сказать, какие стороны многоугольника параллельны. Теперь мы можем записать условия на пары единичных векторов.

Подсказка 4

Знаем, что сумма единичных векторов, где один идёт с коэффициентов 2, а другой - с x равна 0. Также сумма единичных векторов, соответствующим противоположным сторонам тоже равна 0. Как найти x?

Подсказка 5

Чему равна сумма единичных векторов без дополнительных коэффициентов?

Подсказка 6

Их сумма равна 0! Теперь-то мы можем найти x) Осталось лишь найти площадь многоугольника, в котором мы знаем взаимное расположение всех сторон.

Показать ответ и решение

Рассмотрим 12-угольник $A A ...A , 1 2 12$ удовлетворяющий условию задачи. У него десять сторон длины 1 и одна сторона длины 2. Обозначим через $x$ длину оставшейся стороны. Рассмотрим векторы $−−−→ −−−→ −−−−→ A1A2,A2A3,...,A12A1,$ а также коллинеарные им единичные векторы $⃗e1,⃗e2,...,⃗e12.$ Тогда для некоторых $i$ и $j$ имеет место равенство

−→ ⃗e1 +...+ 2⃗ei+...+ x⃗ej +...+⃗e12 = 0

Помимо того,

−→ ⃗e1+ ⃗e7 =⃗e2+ ⃗e8 = ...= ⃗e6 +⃗e12 = 0,

поэтому

−→ ⃗e1+⃗e2+ ...+ ⃗e12 = 0

Вычитая второе из полученных равенств из первого, получаем

⃗ei+ (x− 1)⃗ej = −→0

Это возможно лишь в случае, если $⃗ei = −⃗ej$ и $x = 2.$ Значит, в исходном 12-угольнике есть пара параллельных сторон длины 2.

В силу равенства всех углов и соответствующих сторон этот 12-угольник имеет ось симметрии:

$PIC$

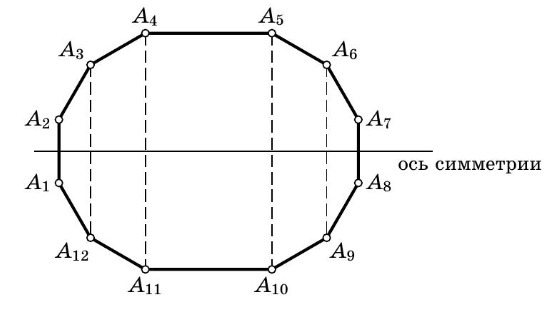
Чтобы найти площадь, разобьём его на 4 трапеции и прямоугольник. Находим $A3A12 = A6A9 = 1+ √3,A4A11 =A5A10 =$ $= 2+√3-$ , поэтому искомая площадь равна

√- √3⋅(2+-√3+-1+-√3) 1+-√3+-1 √- S = 2⋅(2+ 3)+ 2 + 2 = 8+ 4 3

Ответ:

$8+ 4√3$

Ошибка.
Попробуйте повторить позже

Задача 8#76463

На каждой из сторон параллелограмма выбрано по произвольной точке. Точки на соседних сторонах параллелограмма соединены отрезками прямых. В результате от параллелограмма оказываются отсеченными четыре треугольника. Вокруг каждого из этих треугольников описана окружность. Докажите, что центры этих окружностей являются вершинами некоторого параллелограмма.

Источники: Надежда энергетики-2022, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Взглянув на условие, кажется, что надо доказать что-то страшное и непонятно, как это делать. Но давайте вспомним, какие в принципе у нас есть способы решения задач по планиметрии? Углы считать мы не пойдём, в лоб доказывать равенство сторон тоже. Как можно сделать это хитрее?

Показать доказательство

Изобразим окружности и их центры, которые обозначим $O ,...,O . 1 4$ Рассмотрим векторы $O O ,O O 1 2 4 3$ и $O O ,O O . 1 4 2 3$

$PIC$

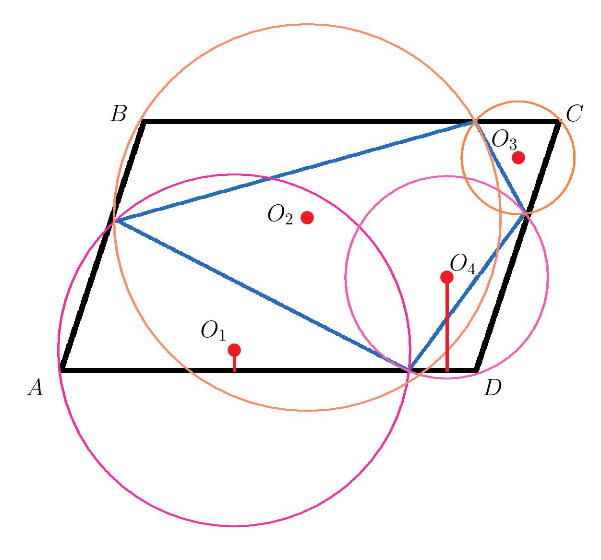
Поскольку центры описанных окружностей лежат на пересечении серединных перпендикуляров, проекции указанных векторов на стороны исходного параллелограмма будут равны половине этих сторон.

Таким образом, если ввести две оси: одну параллельно стороне $AB,$ а другую параллельно стороне $AD,$ то каждая пара рассматриваемых векторов будет иметь одинаковые проекции на каждую из введенных осей. Отсюда следует попарное равенство самих векторов.

Ошибка.
Попробуйте повторить позже

Задача 9#34679

В треугольнике $ABC$ длины сторон равны $4$ , $5$ и $√17-$ . Найдите площадь фигуры, состоящей из тех и только тех точек $X$ внутри треугольника $ABC$ , для которых выполняется условие $2 2 2 XA +XB + XC ≤21$

Источники: ОММО - 2021, номер 4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Расстояния между точками удобно считать, когда есть система координат. Как было бы удобно расположить наш треугольник в декартовой системе координат?

Подсказка 2

Заметим, что высота, проведенная к стороне длины 4, равна целочисленному числу, поэтому удобно ввести систему координат так, чтобы Оу было вдоль этой высоты, а Ох — вдоль упомянутой стороны треугольника. Тогда координаты вершин треугольника принимают целочисленные значения.

Подсказка 3

Пусть (x; y) — координаты X. Тогда выражение XA² + XB² + XC² можно представить как сумму двух квадратов с некоторыми коэффициентами, что очень напоминает уравнение окружности с центром в (x; y). А так как нам дано неравенство, то наша фигура в X — это круг! Останется лишь показать, что все его точки лежат внутри △ABC.

Показать ответ и решение

Первое решение. Обозначим $BC = a,AC = b,AB = c,ρ2 =21$ .

Докажем утверждение, известное как теорема Лейбница в геометрии. Пусть $G$ - точка пересечения медиан треугольника $ABC$ . Представим

−−→ −→ −−→ −−→ −−→ −−→ −−→ −−→ −−→ XA =GA − GX,XB = GB − GX,XC = GC −GX,

тогда

2 2 2 2 2 2 −−→ −→ −−→ −−→ 2 XA + XB +XC = GA + GB +GC − 2⋅GX ⋅(GA + GB +GC )+3⋅GX

Поскольку $G−$ центр тяжести треугольника $ABC$ , то

−G→A +−G−→B + −−G→C = 0,

GA2+ GB2 +GC2 = 4(m2a +m2b + m2c)= 1(a2+ b2+ c2) 9 3

С учётом доказанной выше теоремы задача эквивалентна

1(a2+ b2 +c2)+3 ⋅GX2 ≤ ρ2, 3

то есть неравенство сводится к

GX2 ≤ 1⋅(3ρ2− a2− b2 − c2). 9

Итак, геометрическим местом точек $X$ , удовлетворяющих поставленному условию, является круг радиуса $1∘3ρ2−-a2−-b2−-c2 3$ с центром в точке пересечения медиан треугольника $ABC$ .

Этот круг принадлежит треугольнику, если его радиус не больше, чем одна треть наименьшей из высот $△ABC$ :

1∘--2--2---2--2- -2S△ABC--- 3 3ρ − a − b − c ≤ 3max{a,b,c}.

Значит, при выполнении условия

2 2 2 2 2 2 ( )2 a-+b-+-c-< ρ2 ≤ a-+-b-+-c + 4 ⋅-S△ABC-- 3 3 3 max{a,b,c}

искомая площадь равна $S = π ⋅(3ρ2− a2− b2− c2) 9$ . По формуле Герона найдем площадь треугольника:

1∘----√------√---√------√------ S△ABC = 4 (9+ 17)(9− 17)( 17+ 1)( 17− 1)=8

Вычислим

a2 +b2+ c2 58 S△ABC 8 ---3-----= 3-,max{a,b,c}-= 5

Поскольку $ρ2 = 21$ , условие $(∗)$ выполняется:

58 <21≤ 58+ 256= 1706 3 3 75 75

Значит, ответ: $S = π9 ⋅(63− 58)= 5π9$ .

Второе решение. Высота треугольника, проведенная к стороне длины $4$ , равна $4$ . Основание высоты делит эту сторону на отрезки, равные $1$ и $3$ . Введем систему координат так, как показано на рисунке. Тогда $A(−1;0),B(0;4),C(3;0)$ .

$PIC$

$2 2 2 2 2 2 2 2 2 2 2 XA + XB +XC = (x+ 1) + y + x +(y− 4) + (x− 3) + y =3x + 3y − 4x− 8y+ 26 ≤21.$ Перепишем неравенство так:

( )2 ( )2 x − 2 + y− 4 ≤ 5. 3 3 9

Оно определяет круг радиуса $R = √35$ с центром в точке $K (2∕3;4∕3)$ . Покажем, что все точки этого круга принадлежат треугольнику $ABC$ . Для этого найдем расстояния от точки $K$ до сторон треугольника. Уравнение стороны $AB :4x− y+ 4= 0$ , расстояние до неё равно $|4⋅√(2∕3)−4∕3+4| d1 = 42+(−1)2 =$ $-1√6- = 3 17$ . Уравнение стороны $BC :4x+3y− 12= 0$ , расстояние $|4⋅(2∕3√)+3⋅(4∕3)−12| 16 d2 = 42+32 = 15$ . И расстояние от точки $K$ до стороны $AC$ равно, очевидно, $d3 = 43$ . Наименышее из расстояний $d2$ , тем не менее, больше, чем радиус круга $√- R : 1615-> 35$ . Поэтому весь круг и является той фигурой, площадь которой требуется найти, откуда $S =πR2 = 59π$ .

Ответ:

$5π 9$

Ошибка.
Попробуйте повторить позже

Задача 10#92175

Существует ли такой выпуклый четырёхугольник, у которого длины всех сторон и диагоналей в некотором порядке образуют геометрическую прогрессию?

Источники: ММО - 2021, второй день, 11.4 (см. mmo.mccme.ru)

Показать ответ и решение

Пусть $a$ — некоторое положительное число. Треугольник со сторонами $1,a$ и $a2$ существует тогда и только тогда, когда выполняются три неравенства:

2 2 2 1< a+ a, a< 1+a , a < a+ 1.

Первое из этих неравенств выполнено при $a > 1 φ$ , второе — при всех положительных $a$ , третье — при $a< φ$ , где $φ= 1+√5 2$ — так называемое «золотое сечение», положительный корень квадратного уравнения $x2 − x− 1= 0$ . Следовательно, треугольник с такими сторонами существует при $a∈( 1;φ ) φ$ . При таких же $a$ существует треугольник со сторонами $1, 1 a$ и $1- a2$ . Пусть далее значение $a$ принадлежит отрезку $√-- (1 ) [1; φ]⊂ φ;φ$ .

В декартовой системе координат $Oxy$ отметим точки $O(0,0)$ , $B (1,0)$ , точку $A$ в полуплоскости $y > 0$ , для которой $2 OA = a$ и $AB = a$ , а также точку $C$ в полуплоскости $y < 0$ , для которой $1 OC = a2$ и $1 CB = a :$

$PIC$

По доказанному выше такие точки существуют для всех $a ∈[1;√ φ]$ . Кроме того, треугольники $OAB$ и $OBC$ подобны по трем пропорциональным сторонам. Значит, $∠AOB = ∠BOC$ и $∠OAB = ∠OBC$ . Поскольку $1≤ a≤ a2$ , угол $AOB$ , лежащий напротив стороны а треугольника $OAB$ , меньше $90∘$ . Отсюда получаем, что

∘ ∠AOC =2∠AOB <180

∠ABC =∠ABO +∠OBC =∠ABO +∠OAB <180∘

Следовательно, $OABC$ — выпуклый четырехугольник при всех указанных значениях $a$ .

Пусть точка $A$ имеет координаты $(x;y)$ , тогда $x2+y2 =$ $= a4$ и $(x− 1)2+ y2 = a2$ . Из этих уравнений получаем

4 2 x= a-−-a-+-1= f(a) 2

-------- y =∘ a4− f2(a)

Эти выражения непрерывно зависят от $a$ на отрезке $[1;√ φ]$ . Аналогично доказывается, что координаты точки $C$ также непрерывно зависят от $a$ на этом отрезке. Следовательно, длина диагонали $AC$ четырехугольника $OABC$ , равная $g(a)$ , также непрерывно зависит от $a$ на этом отрезке.

При $a= 1$ треугольники $OAB$ и $OBC$ являются равносторонними со стороной 1 , поэтому $g(1)= √3$ . При $a= √φ-$ получаем

√ -- √ -- -1- 1+-φ √--3 g( φ)=AC < AB + BC = φ+ √φ-= √φ-= ( φ) .

Значит, непрерывная на отрезке $√ -- [1; φ]$ функция $g(a)− a3$ принимает в концах этого отрезка значения разных знаков:

√- g(1)− 13 = 3− 1> 0

g(√φ)− (√φ)3 < 0

Поэтому найдется такое значение $√ -- a ∈(1; φ)$ , при котором $g(a)− a3 = 0$ и, следовательно,

OC = -12,CB = 1,OB =1,AB = a,OA = a2,AC = a3 a a

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 11#76942

Математический бильярд имеет форму параллелограмма $ABCD$ . На сторонах $AD$ и $CD$ соответственной расположены точки $E$ и $F$ так, что $AE :ED =1 :2$ , а $DF :FC =1 :3$ . Шар находится в точке $M$ пересечения прямых $BF$ и $CE$ . Известно, что шар, направленный в точку $N$ борта $BC$ , отразившись от четырех различных бортов, вернулся в точку $M$ и, продолжив свое движение, повторил свою предыдущую траекторию. Найти величину отношения $BN$ : $NC$ , если известно, что траектория шара — выпуклый четырехугольник.

Показать ответ и решение

Рассмотрим траекторию движения, следуя правилу "угол падения равен углу отражения". Пусть эти углы равны $α ,α ,α ,α 1 2 3 4$ для случаев отражения от бортов $BC$ , $AB$ , $AD$ , $CD$ соответственно. Тогда выполняются равенства $α1+ α4 = α2+α3$ и $α1+ α2 = α3+ α4$ из тех соображений, что противоположные углы параллелограмма равны. Из этих равенств вытекает, что $α1 = α3$ и $α2 = α4$ , из чего, в свою очередь, следует, что $ABCD$ – прямоугольник.

$PIC$

Введём аффинную систему координат, в которой $A(0;0)$ , $D(1;0)$ , $B(0;1)$ , $C(1;1)$ и выпишем уравнения прямых $CE$ и $BF$ . Поскольку $E(13;0)$ и $F(1;14)$ , прямые $CE$ и $BF$ задаются уравнениями:

y = 3x− 1 и y = − 3x+1 2 2 4

соответственно, а их точкой пересечения будет $M (2;1). 3 2$

Теперь отразим прямоугольник $ABCD$ зеркально сначала от стороны $BC$ , затем от стороны, в которую перешла $BC$ при этом отражении, и далее для двух оставшихся сторон по тому же принципу. Это стандартная процедура "выпрямления"бильярдной траектории, соответствующая равенству угла падения углу отражения.

$PIC$

При таких "зеркальных"отражениях траектория становится отрезком $MM ′$ , где $M ′$ - образ точки $M$ после серии отражений. Её координаты легко вычислить: после четырёх отражений прямоугольник сохранил ориентацию, и сдвинулся на два размера влево и на два размера вверх. Таким образом, $M ′(23 − 2;12 + 2)$ , и прямая $MM ′$ имеет угловой коэффициент $− 1$ . Её уравнением будет

y =− x+ 7 6

и прямую $BC$ , заданную уравнением $y = 1$ , она пересекает в точке с абсциссой $x= 16$ . Это значит, что точка $N$ , в которую был направлен шар, делит отрезок $BC$ в отношении $1:5$ .

Ответ: 1 : 5

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#43116

Вершины $K,L,M,N$ четырехугольника $KLMN$ лежат соответственно на сторонах $AB,BC,CD, DA$ квадрата $ABCD$ . Найти наименьший возможный периметр четырехугольника $KLMN$ , если $AK = 2$ см, $BK =4$ см и $AN =ND$ .

Источники: ОММО-2010, номер 7, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Очень часто, когда просят найти наименьший периметр, помогает сводить задачу к неравенству ломаной. Т.е. все нужные нам отрезки "сложить" в одну ломаную. Каким образом это удобнее всего сделать в нашем случае, учитывая, что у нас квадрат?

Подсказка 2

Квадрат удобно отражать и переносить. Осталось лишь подумать, относительно каких сторон это делать, чтобы каждый раз у нас появлялся новый кусочек ломаной, которую хотим создать из нужных отрезков.

Показать ответ и решение

Первое решение.

$PIC$

(везде ниже единицы измерения — сантиметры)

Из первого условия $AB =6 =⇒ AN = ND = 3$ . Сведём задачу к неравенству ломаной. Для этого отразим квадрат относительно $CD$ ( $A → A′,B → B′$ ), а затем относительно $BC ′$ ( $D → D ′,A′ → A′′,M → M ′$ ). Легко видеть, что $LM = LM ′$ . Далее отразим $N$ относительно $C$ в точку $N′ ∈ D′A ′′$ . Можно считать, что точку $M$ мы ранее также отражали относительно $C$ , потому $M ′N ′ =MN$ . По неравенству ломаной $KN ′ ≤ KL+ LM ′+M ′N′ = PKLMN − NK$ . Отрезок $NK =√32-+22 = √13$ фиксирован, потому достаточно посчитать длину $KN ′$ (нетрудно видеть, что минимум достигается подбором точек $L$ и $M$ ). Используем теорему Пифагора $xKN ′ =6 +3= 9$ (“проекция на $Ox$ ”) и $yKN′ = 4+ 6= 10$ , откуда $KN ′ = √181$ .

Второе решение.

Введём систему координат с центром в точке $A$ , ось $Ox$ направим вдоль $AD$ , ось $Oy$ вдоль $AB$ , возьмём за единицу измерения $1$ см. Обозначим координату точки $L$ по оси $x$ за $a$ , координату точки $M$ по оси $y$ — за $b$ . Тогда по теореме Пифагора периметр четырёхугольника $KLMN$ равен $√a2-+42+ ∘ (6−-a)2+(6−-b)2+ ∘32+-y2+ √32+-22-$ .

Отметим точки с соответствующими им координатами: $R(a;4),P (6;10− b);Q(9;10)$ . По неравенству ломаной $AR + RP +PQ ≥ AQ =√92-+102,$ причём равенство достигается при $x = -6--= 9- =⇒ a= 18,b = 10. 4 10−b 10 5 3$

Итак, минимальный периметр равен $√92-+102+ √32+-22.$

Ответ:

$√13-+√181$ см

Ошибка.
Попробуйте повторить позже

Задача 13#97589

Хорды $AC$ и $BD$ окружности с центром $O$ пересекаются в точке $K.$ Пусть $M$ и $N$ — центры описанных окружностей треугольников $AKB$ и $CKD$ соответственно. Докажите, что $OM = KN.$

Показать доказательство

Рассмотрим проекции $−M−−−→O 1 1$ и $−−K−N→ 1$ векторов $−M−→O$ и $−K−→N$ на хорду $AC.N 1$ — середина хорды $KC$ , поэтому

−−−→ 1−−→ KN1 = 2KC

$M1$ и $O1$ — середины хорд $AK$ и $AC$ , поэтому

−−−−→ −−→ −−−→ 1−→ 1−−→ 1−−→ M1O1 =AO1 − AM1 = 2AC− 2AK = 2KC

Таким образом, $−−−−→ −−−→ M1O1 =KN1$ .

Аналогично равны проекции векторов $−−M→O$ и $−−K→N$ на хорду $BD$ . Но вектор полностью определяется своими проекииями на две непараллельные прямые. Поэтому $−M−O→ =−K−N→.$

Предыдущий раздел

Следующий раздел