tmp (работа над текущими задачами)
Ошибка.
Попробуйте повторить позже
Докажите, что при
выполнено неравенство
Ошибка.
Попробуйте повторить позже
Попарно различные действительные числа
и
удовлетворяют условию
Чему может быть равно
Ошибка.
Попробуйте повторить позже
Упростить выражение
и найти его значение при
Источники:
9
Ошибка.
Попробуйте повторить позже
Имеется два сплава меди и олова. Первый весит 5 кг и содержит меди, второй весит 3 кг и содержит
меди.
Какого веса надо взять куски этих сплавов, чтобы после их совместной переплавки получить 4 кг сплава, содержащего
меди?
Источники:
При нужно взять
кг первого сплава и
кг второго сплава; при
такой сплав получить
невозможно.
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Ошибка.
Попробуйте повторить позже
О треугольнике известно, что длины сторон
и диаметр вписанной окружности являются последовательными членами
арифметической прогрессии. Найдите периметр треугольника, если диаметр вписанной окружности равен 6.
Источники:
36
Ошибка.
Попробуйте повторить позже
Решите систему уравнений
если .
Источники:
Ошибка.
Попробуйте повторить позже
Какое наибольшее количество квадратиков можно поместить, располагая стороны квадратиков по линиям сетки, в
клеточный прямоугольник
если любым двум квадратикам можно иметь либо одну общую клеточку, либо ни
одной?
Источники:
312
Ошибка.
Попробуйте повторить позже
Даны многочлены и
оба степени
со старшими коэффициентами
У каждого из них ровно
различных целых корней.
Известно, что все корни многочлена
четны, а все корни многочлена
нечетны. Докажите, что у многочлена
не
может быть целых корней.
Источники:
Ошибка.
Попробуйте повторить позже
Дана двусторонняя линейка без делений. Этот инструмент позволяет делать две операции:
1) провести прямую через две данные точки;
2) провести прямую, параллельную данной, на расстоянии 1 от нее.
Постройте с ее помощью (и не используя никакие другие инструменты) правильный треугольник.
Источники:
Ошибка.
Попробуйте повторить позже
На плоскости отмечено 8 точек, никакие три из которых не лежат на одной прямой. Между каждыми двумя проведен либо красный, либо синий отрезок. Красные отрезки не имеют общих точек, кроме, возможно, отмеченных точек. Обязательно ли найдется треугольник с вершинами в отмеченных точках, все стороны которого синие?
Источники:
Не обязательно
Ошибка.
Попробуйте повторить позже
Разрежьте фигуру, составленную из одинаковых равносторонних треугольников (см. рисунок), на три (не обязательно равные) части и сложите из них равносторонний треугольник.
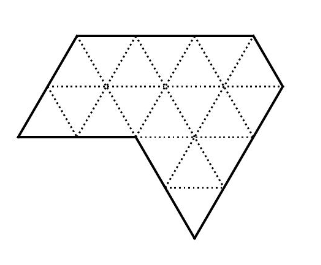
Источники:
Ошибка.
Попробуйте повторить позже
По кругу стоит несколько коробок. В одной из них 2025 камней, а остальные пусты. Разрешается взять два камня (возможно, из разных коробок) и переложить один в соседнюю коробку по часовой стрелке, а другой — в соседнюю против часовой стрелки. Через некоторое время все камни оказались в одной и той же коробке, соседней с начальной. Докажите, что один из камней побывал во всех коробках.
Источники:
Ошибка.
Попробуйте повторить позже
Существует ли функция определенная на всей числовой прямой, такая, что для любого
выполнено равенство
Источники:
Не существует
Ошибка.
Попробуйте повторить позже
Назовем год замечательным, если номер года делится на сумму двузначных чисел, из которых этот номер составлен. Например, год —
замечательный, поскольку
делится на
Сколько ещё замечательных годов в XXI веке (с
по
год
включительно)?
Источники:
Ошибка.
Попробуйте повторить позже
При каких положительных значениях и
достигается наибольшее значение выражения?
Источники:
Ошибка.
Попробуйте повторить позже
Квадрат со стороной
и квадрат
со стороной
имеют общую вершину
при этом точка
лежит на отрезке
Найдите наибольшее и наименьшее возможные значения площади параллелограмма
если точка
лежит на отрезке
и
делит его в отношении
Источники:
Ошибка.
Попробуйте повторить позже
На доске записано 7 различных чисел, сумма которых равна 10. Петя умножил каждое из них на сумму остальных шести и записал 7 полученных произведений в тетрадь. Оказалось, что в тетради встречаются только четыре различных числа. Найдите одно из чисел, записанных на доске.
Источники:
-20
Ошибка.
Попробуйте повторить позже
На окружности длиной 1 метр отмечена точка. Из неё в одну и ту же сторону одновременно побежали два таракана с различными постоянными скоростями. Каждый раз, когда быстрый таракан догонял медленного, медленный мгновенно разворачивался, не меняя скорости. Каждый раз, когда они встречались лицом к лицу, быстрый мгновенно разворачивался, не меняя скорости. На каком расстоянии от отмеченной точки могла произойти их сотая встреча?
Источники:
на нулевом
Ошибка.
Попробуйте повторить позже
На стороне остроугольного треугольника
выбраны точки
и
так, что
Точки
и
выбраны
соответственно на отрезках
и
так, что
и
Докажите, что точка пересечения медиан треугольника
равноудалена от прямых
и
Источники:



