04 Законы сохранения в механике
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Маятник массы отклонили на угол
от положения равновесия и отпустили без начальной скорости. Найдите силу натяжения
нити в момент прохождения маятником положения равновесия. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
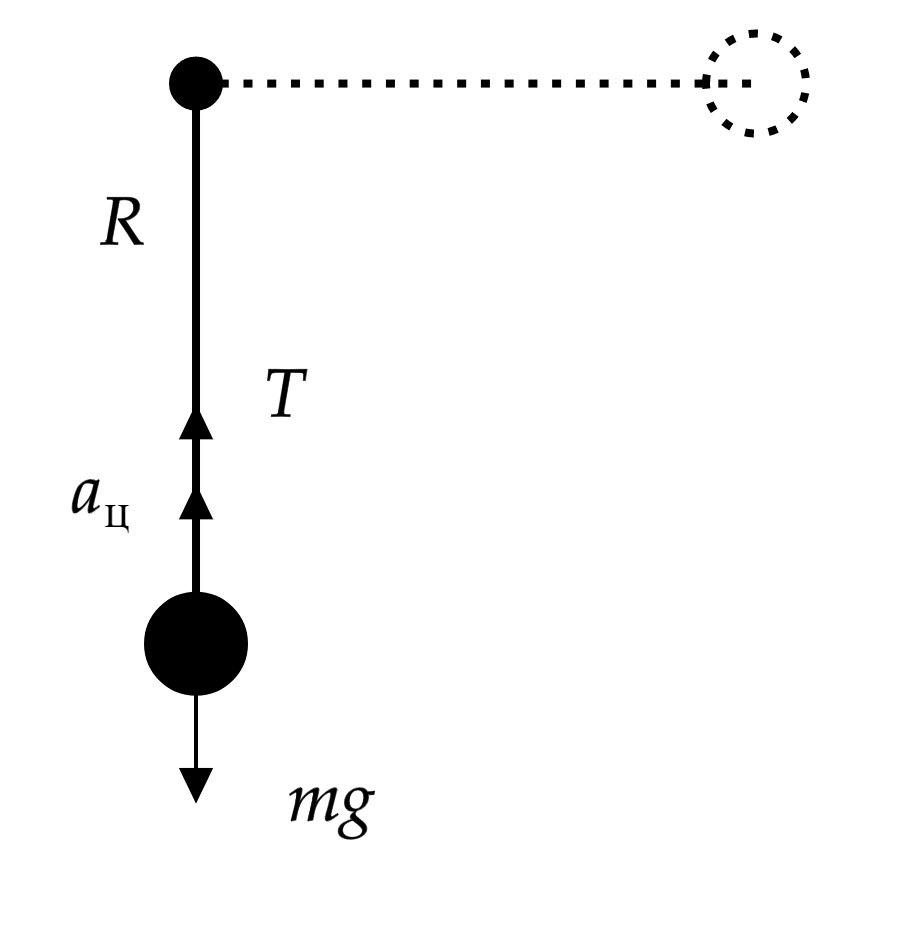
Пусть в начальный момент времени маятник находился на высоте от положения равновесия и обладает потенциальной
энергие
, а
– скорость маятника в положении равновесия и тело обладает кинетической энергией
. Тогда из закона
сохранения энергии
Запишем второй закон Ньютона, где – сила натяжения нити
где – центростремительное ускорение.
Спроецируем второй закон Ньютона на вертикальную нить:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление для момента прохождения телом нижней точки
траектории, закон сохранения механической энергии, формулы потенциальной и кинетической
энергии, формула центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Маятник массы отклонили на угол
от положения равновесия и отпустили без начальной скорости. Найдите силу
натяжения нити в момент прохождения маятником положения равновесия. Какие законы Вы используете для решения задачи?
Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
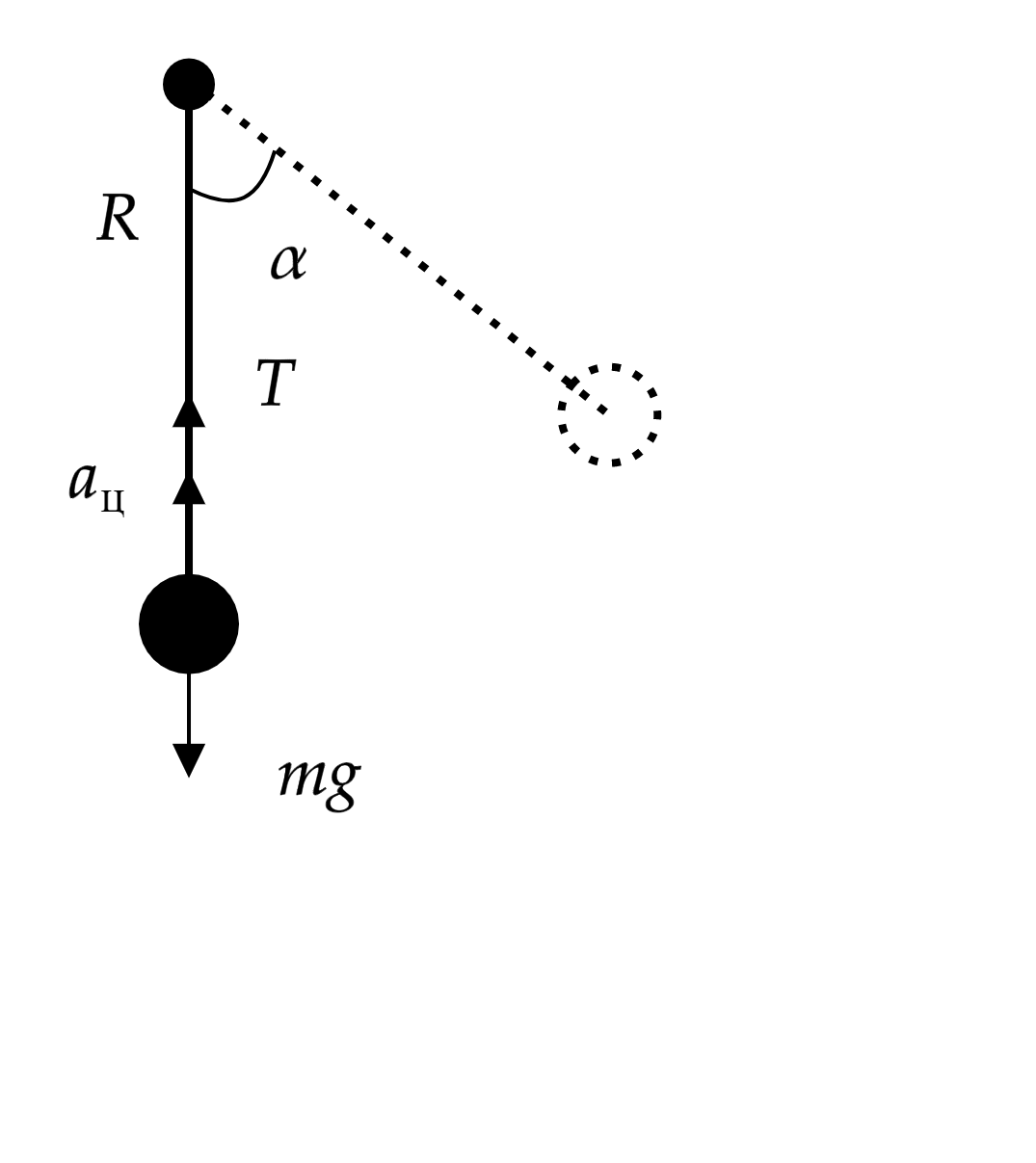
Пусть длина нити равна , тогда высота нахождения маятника в начальный момент времени
, а
– скорость
маятника в положении равновесия. Тогда из закона сохранения энергии
Здесь - потенциальная энергия тела при отклонении его на угол
,
- кинетическая энергия при
прохождении нижней точки траектории.
Запишем второй закон Ньютона, где – сила натяжения нити
где – центростремительное ускорение.
Спроецируем второй закон Ньютона на вертикальную нить:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
______________________________________________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
________________________________________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи
выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на радиальное направление для
момента прохождения телом нижней точки траектории, закон сохранения механической энергии, формулы потенциальной и
кинетической энергии, формула центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
________________________________________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются
один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
________________________________________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Маленький груз висит в покое на невесомой нерастяжимой нити длины . Какую минимальную горизонтальную скорость
надо
сообщить грузу, чтобы он совершил полный оборот в вертикальной плоскости? Какие законы Вы используете для решения задачи?
Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
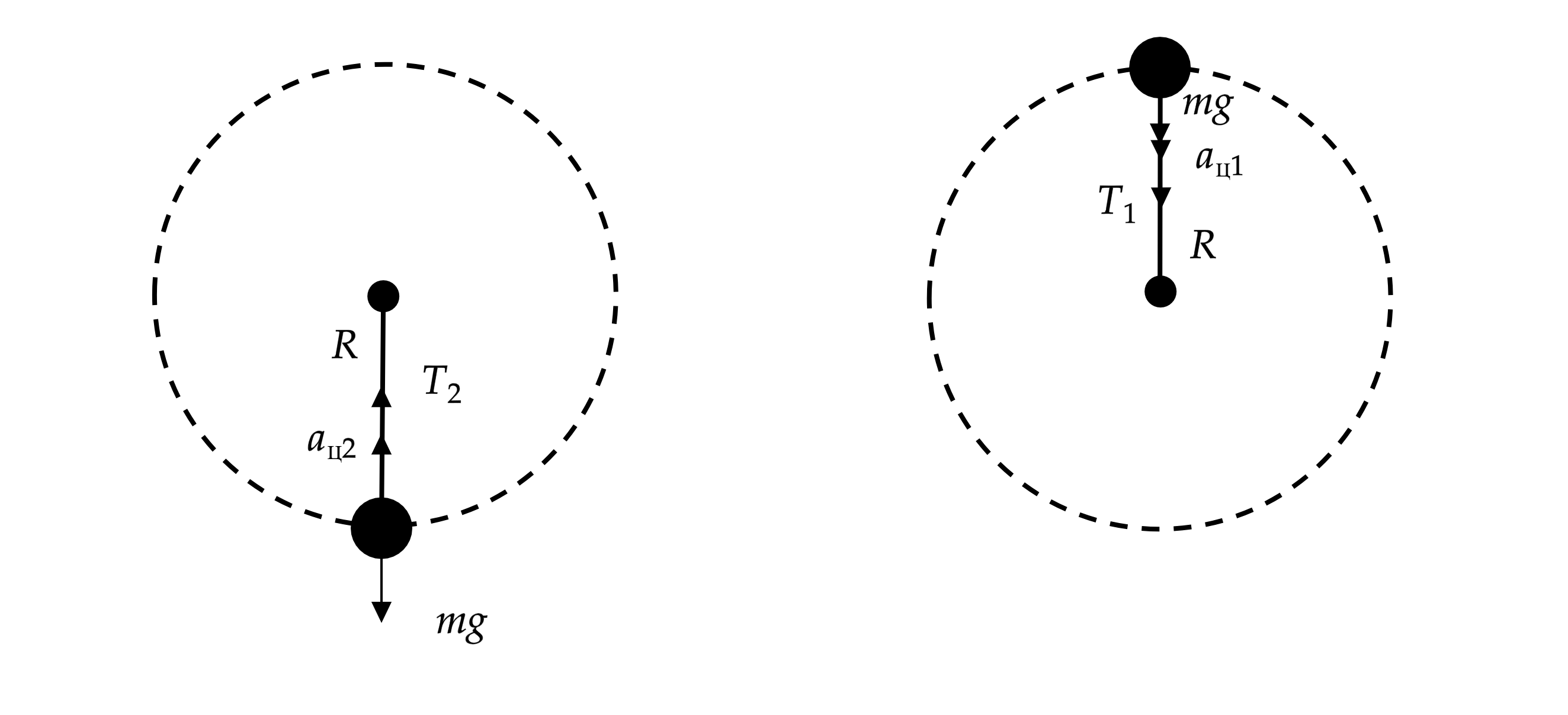
Пусть скорость маятника в верхней точке равна . Тогда из закона сохранения энергии
Запишем второй закон Ньютона:
где – сила натяжения нити,
– центростремительное ускорение. Условие минимальности скорости означает, что сила
натяжения нити в верхней точке равна 0. Иногда предполагают именно нулевую скорость, что является ошибочным, если скорость в
верхней точке будет равна 0, то тело в наивысшей точке вращения просто начнет падать вертикально вниз. Спроецируем второй
закон Ньютона на вертикальную ось в верхней точке
Тогда минимальная начальная скорость
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано наличие центростремительного ускорения
______________________________________________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
________________________________________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи
выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на радиальное направление,
формула центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
________________________________________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются
один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
________________________________________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Маленький шарик, подвешенный на нити, может вращаться в вертикальной плоскости вокруг оси O. Экспериментатор обнаружил,
что наименьшая скорость, которую нужно сообщить шарику, чтобы он достиг верхней точки траектории (точки A), равна . Затем
экспериментатор заменил нить лёгким стержнем той же длины, который может без трения вращаться вокруг оси O. Какую
минимальную скорость нужно сообщить шарику теперь, чтобы он достиг точки A? Какие законы Вы используете для решения
задачи? Обоснуйте их применение.
(МОШ, 2019, 10 )
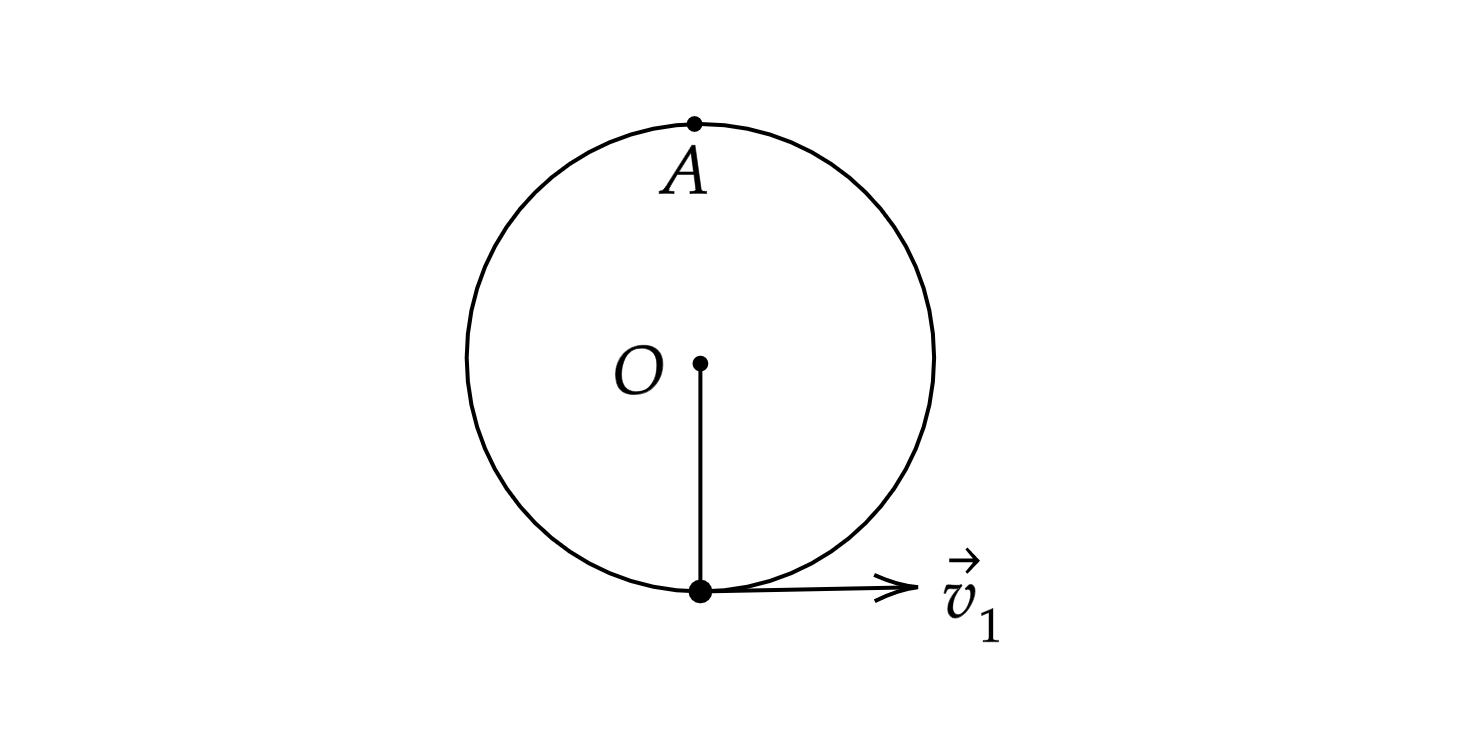
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
6. Когда тело закреплено на стержне, то в нем возникает сила реакции опоры, эта сила является непотенциальной силой. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
Решение
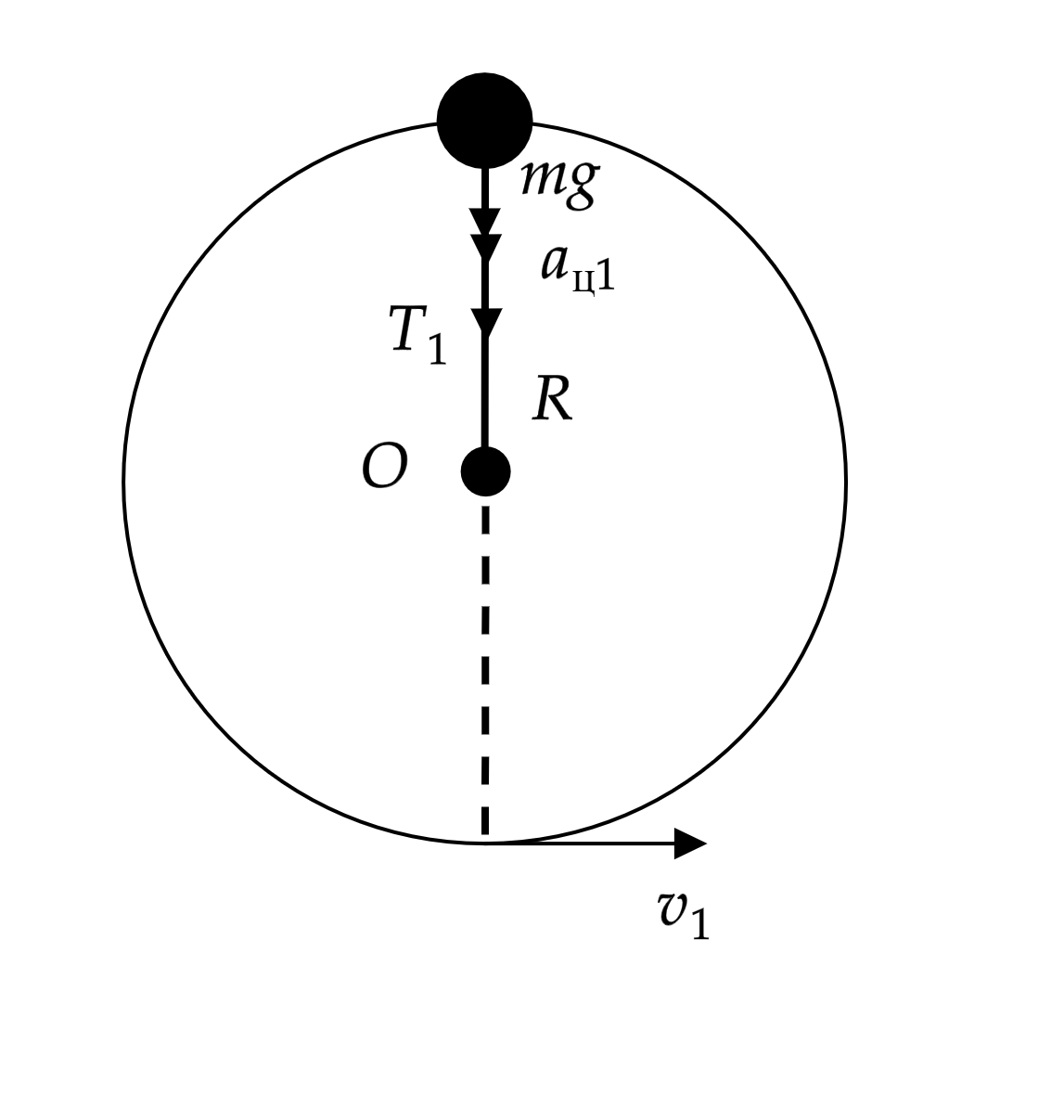
Кинетическая энергия тела рассчитывается по формуле , потенциальная энергия находится по формуле
, где
- высота, на
которой находится тело,
- скорость, которой обладает тело.
Пусть длина нити скорость маятника в верхней точке равна
. Тогда из закона сохранения энергии
Запишем второй закон Ньютона для верхней точки:
где – сила натяжения нити,
– центростремительное ускорение. Условие минимальности скорости означает, что сила
натяжения нити в верхней точке равна 0. Иногда предполагают именно нулевую скорость, что является ошибочным, если скорость в
верхней точке будет равна 0, то тело в наивысшей точке вращения просто начнет падать вертикально вниз. Спроецируем второй
закон Ньютона на вертикальную ось в верхней точке
Тогда минимальная начальная скорость
В отличии от нити, скорость стержня может быть приблизительно равна 0 в верхней точке траектории (в условиях задачи можно использовать 0), тогда из закона сохранения энергии, минимальная начальная скорость равна
Откуда
Дополнение к задаче
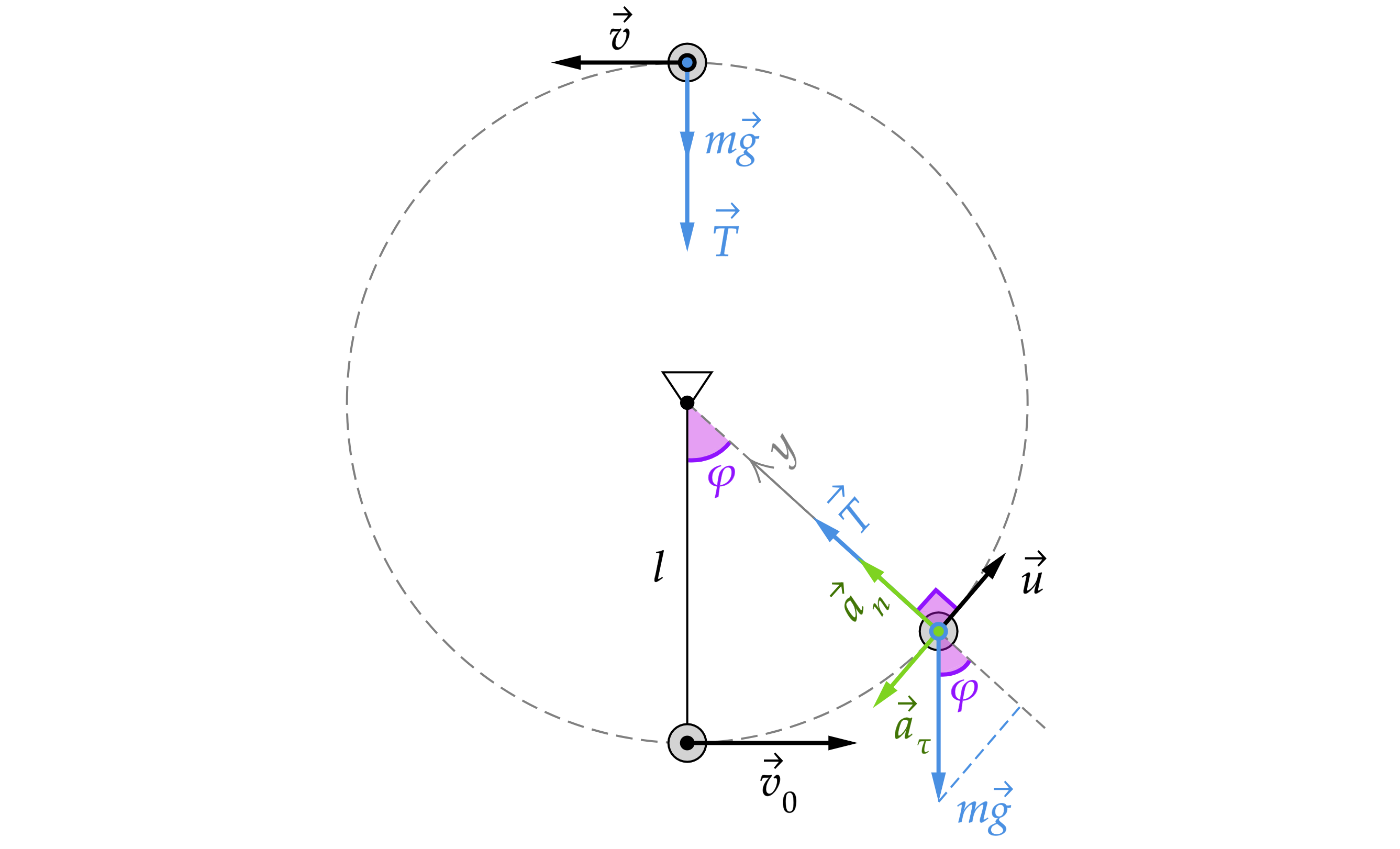
Чтобы доказать, что минимальная сила натяжения будет в верхней точке запишем второй закон Ньютона для положения,
изображенного на рисунке
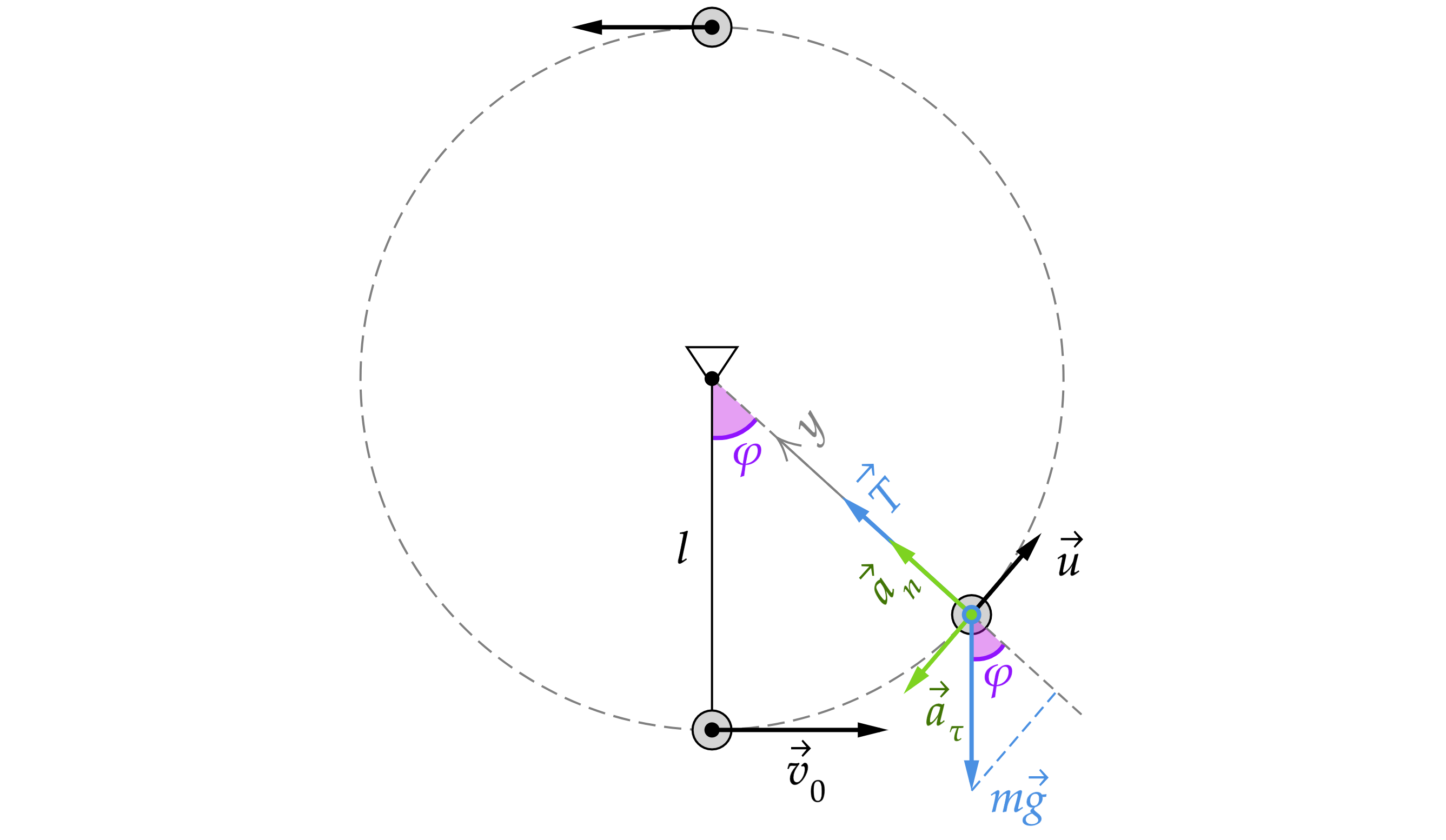
в проекции на ось и
распишем центростремительное ускорение
Тогда
минимальное значение выражение принимает при , то есть в верхней точке траектории.
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление для момента прохождения телом нижней точки
траектории, закон сохранения механической энергии, формулы потенциальной и кинетической
энергии, формула центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Маленький груз висит в покое на невесомой нерастяжимой нити длины . Грузу сообщают горизонтальную скорость
. На
какой высоте
(над начальным положением груза) ослабнет нить? Опишите дальнейшее движение груза. Какие законы Вы
используете для решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
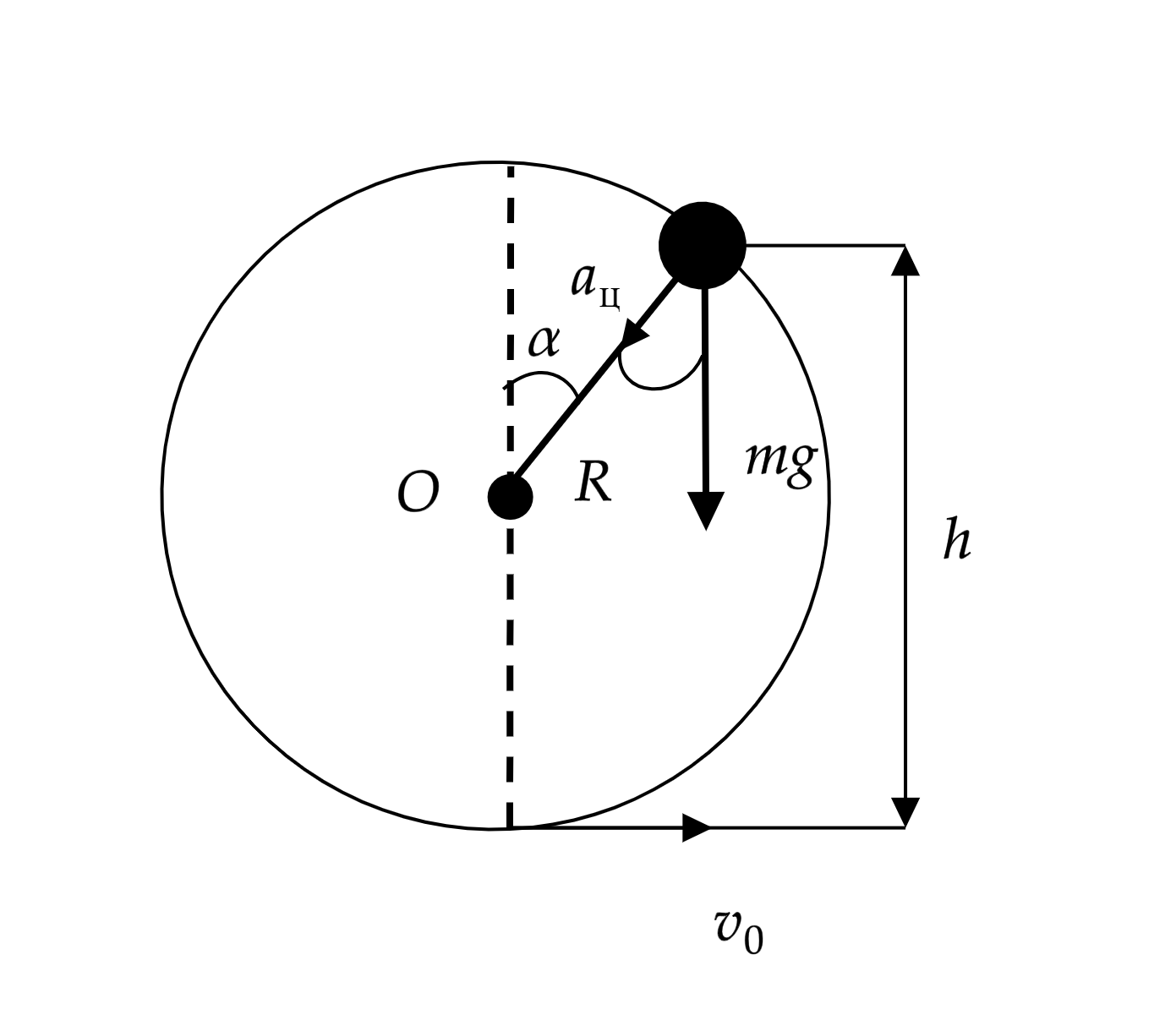
Второй закон Ньютона для тела запишется в виде:
где – сила натяжения нити,
– полное ускорение.
Ослабление нити означает, что . Пусть в момент ослабления нити скорость равен
, а угол между вертикалью и нитью
равен
, центростремительное ускорение
, тогда второй закон Ньютона на ось, совпадающую с осью нити можно
записать в виде
Также запишем закон сохранения энергии
Здесь - кинетическая энергия в начальный момент времени,
- потенциальная энергия в точке, где нить ослабнет,
- кинетическая энергия в той точке, где нить ослабнет.
Проанализируем начальную скорость, чтобы тело поднялось не выше, чем , его скорость должна составлять
Следовательно, тело поднялось выше , откуда следует, что высота подъема равна
Подставим (1) и (3) в (2)
Откуда высота подъема
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
______________________________________________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
________________________________________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи
выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на радиальное направление для
момента ослабления нити, закон сохранения механической энергии, формулы потенциальной и кинетической энергии, формула
центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
________________________________________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются
один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
________________________________________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
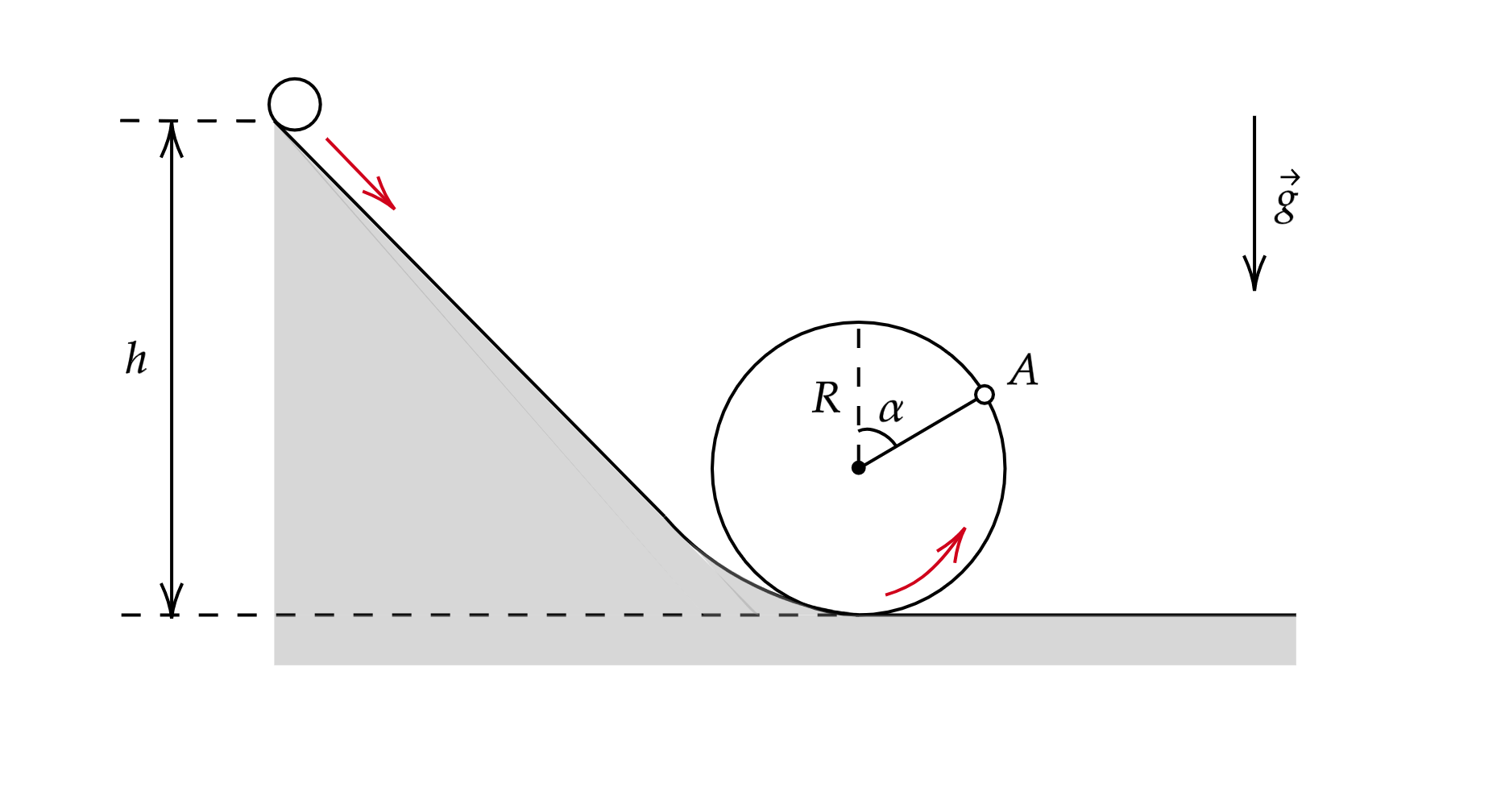
Маленький шарик массой проходит мёртвую петлю радиуса
, соскальзывая без начальной скорости с минимально
необходимой для этого высоты (см. рисунок). Найдите силу давления шарика на опору в точке
, радиус-вектор которой
составляет угол
с вертикалью. Трением пренебречь. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй и третий законы Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
Сделаем рисунок сил
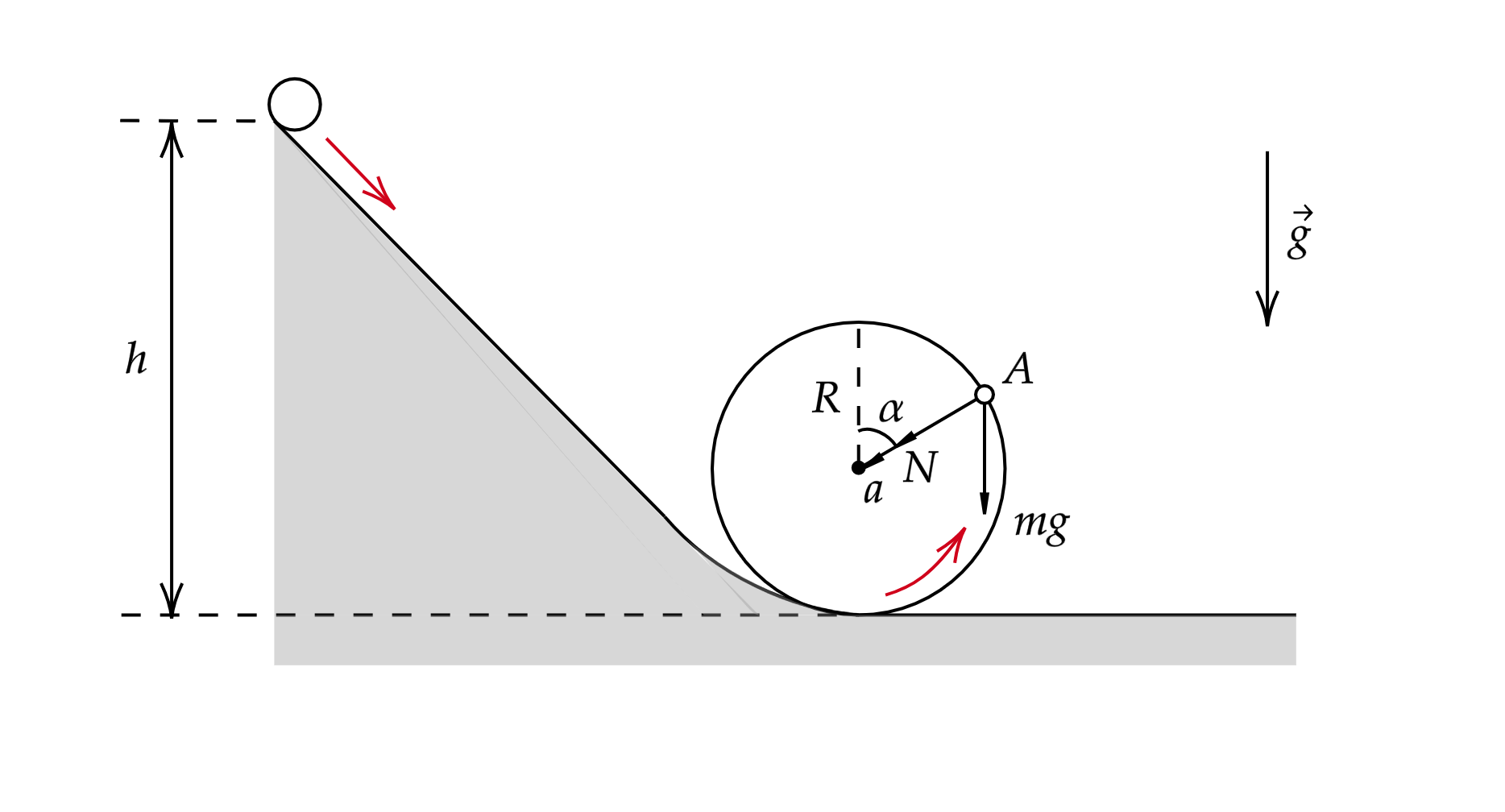
Где – сила реакции опоры,
– центростремительное ускорение,
– полное ускорение,
– сила тяжести.
Запишем второй закон Ньютона:
Для того, чтобы тело прошло петлю, необходимо, чтобы сила реакции опоры во время прохождения ни разу не была равна 0,
минимальная сила реакции опоры наблюдается в верхней точке движения. Докажем это
Пусть угол между силой тяжести и силой реакции опоры равен , тогда второй закон Ньютона запишется в виде
Тогда из закона сохранения энергии
Тогда второй закон Ньютона запишется в виде
Для того, чтобы найти вспомним, что
это минимальная высота, которая требуется, чтобы пройти петлю. Следовательно,
для ее нахождения требуется рассмотреть минимальный случай прохождения петлю. То есть, равенство нулю
в верхней
точке.
Из закона сохранения энергии скорость в верхней точке
Примем в верхней точке силу реакции опоры равно 0, тогда
Тогда скорость тела в точке А
Запишем второй закон Ньютона в проекции на ось, направленную в центр траектории:
По третьему закону Ньютона сола давления на опору вточке равняется силе, с которой опора давит на шарик в этой точке, то
есть равна силе реакции опоры в точке
.
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго и третьего законов Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление для момента прохождения телом токи , третий закон
Ньютона, закон сохранения механической энергии, формулы потенциальной и кинетической энергии,
формула центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Маленький шарик массой проходит мёртвую петлю радиуса
, соскальзывая без начальной скорости с высоты
. Трения
нет.
а) Найдите полное ускорение шарика в момент, когда его скорость вертикальна.
б) На какой высоте сила давления шарика на опору равна ?
Сделаем рисунок сил
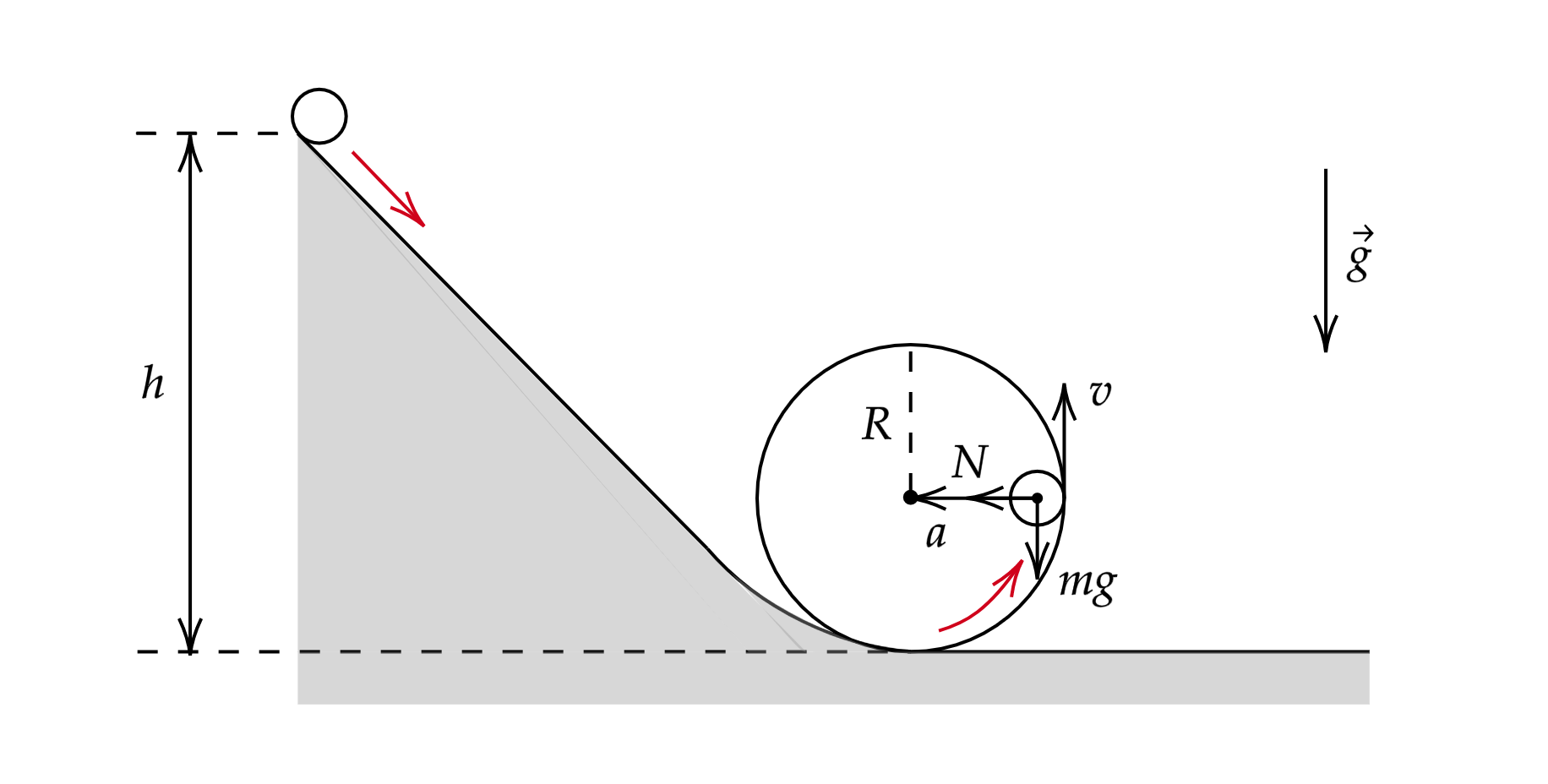
Где – сила реакции опоры,
– полное ускорение,
– сила тяжести,
– скорость шарика.
а) Скорость тела направлена по касательной к окружности, значит, тело должно находиться в крайней правой (левой) точке петли
(см. рис.). Найдем скорость шарика из закона сохранения энергии
Запишем второй закон Ньютона:
Запишем второй закон Ньютона на вертикальную ось
По горизонтальной оси у тела присутствует центростремительное ускорение, равное
Откуда полное ускорение
б) Пусть угол между центростремительным ускорением и силой тяжести равен , тогда скорость на искомой высоте
равна
Рассмотрим два случая. Первый случай, сила тяжести сонаправлена с силой реакции опоры
По условию , тогда
Откуда высота
Теперь рассмотрим случай разнонаправленности и
Косинус не может быть больше 1, следовательно, такая ситуация невозможна
Ошибка.
Попробуйте повторить позже
Гладкая сфера радиуса закреплена на горизонтальном столе. Маленький брусок начинает движение из верхней точки сферы без
начальной скорости. На какой высоте над поверхностью стола брусок оторвётся от сферы? Какие законы Вы используете для
решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение

Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести. Запишем второй закон Ньютона
где – сила реакции опоры,
– полное ускорение
Так как , то с учетом формулы центростремительного ускорения
где
– скорость тела, второй закон Ньютона на
ось
:
С учетом того, что имеем
Также запишем закон сохранения энергии
где – потенциальная энергия тела на высоте
,
– кинетическая энергия на высоте
,
– потенциальная энергия на высоте
. Расписав все слагаемые по формулам получим
Объединим (1) и (2):
При этом искомое расстояние равно:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление, закон сохранения механической энергии, формулы
центростремительного ускорения, кинетической и потенциальной энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Небольшой шарик соскальзывает без начальной скорости и без трения с верхней точки сферы, закреплённой на горизонтальной
поверхности стола.
а) Под каким углом к поверхности стола шарик ударится о стол?
б) На какую максимальную высоту поднимется шарик после упругого удара о стол, если радиус сферы равен ?

Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести. Запишем второй закон Ньютона
где – сила реакции опоры,
– центростремительное ускорение Так как
, то с учетом формулы
центростремительного ускорения
где
– скорость тела.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Также запишем закон сохранения энергии
где – потенциальная энергия тела на высоте
,
– кинетическая энергия на высоте
,
– потенциальная энергия на высоте
,
отсчитывается от центра сферы. Расписав все слагаемые по формулам
получим
Объединим (1) и (2):
При этом расстояние равно:
Мы нашли точку отрыва тела от поверхности сферы.

Скорость направлена перпендикулярно центростремительному ускорению, следовательно
Скорость тела в момент отрыва
Тогда горизонтальная и вертикальная составляющие скорости
Горизонтальная составляющая скорости не изменяется во время полета, значит справедливо равенство:
где – скорость в нижней точке полёта,
– искомый угол.
Запишем закон сохранения полной энергии при всем движении
Отсюда
Так как горизонтальная составляющая часть скорость сохраняется при движении тела, то закон сохранения энергии запишется в виде:
где – искомая высота.
Тогда
Ошибка.
Попробуйте повторить позже
Маленький шарик входит в мёртвую петлю радиуса , соскальзывая без начальной скорости с высоты
. На какой
высоте шарик оторвётся от поверхности петли? Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень, на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
Пусть – сила реакции опоры,
– центростремительное ускорение,
– сила тяжести,
– угол между силой тяжести и
центростремительным ускорением.
Запишем второй закон Ньютона:
В момент отрыва от петли будет равна 0, значит второй закон Ньютона запишется в виде
Найдем скорость тела в момент отрыва, как разность потенциальных энергий
Подставляем (2) в (1) и находим
Откуда высота отрыва
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление для момента прохождения телом точки отрыва, закон
сохранения механической энергии, формулы потенциальной и кинетической энергии, формула
центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
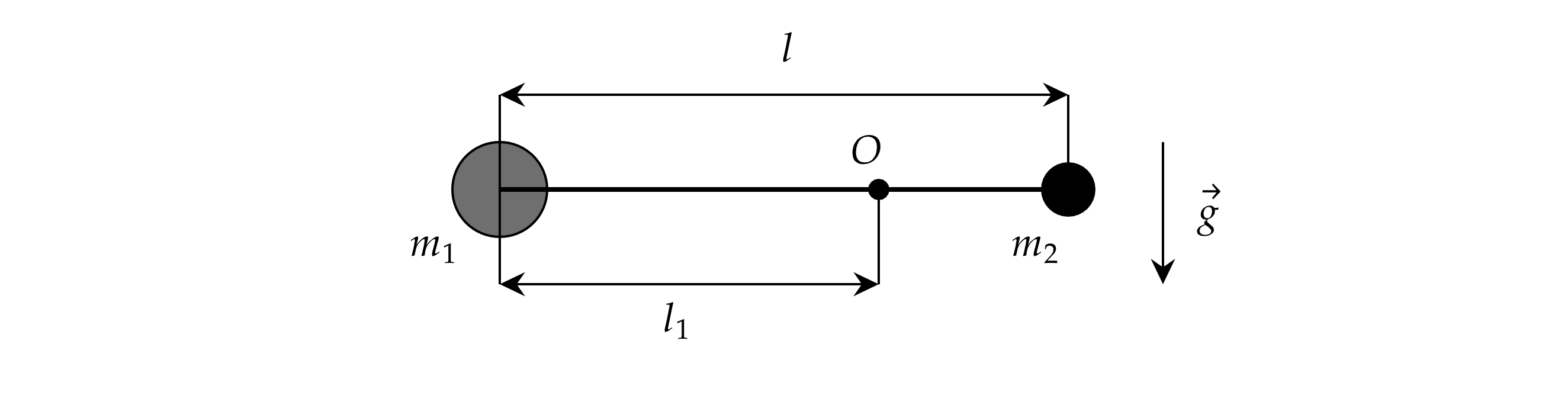
Два небольших груза массами и
г закреплены на невесомом жёстком стержне длиной
.
Стержень может вращаться без трения вокруг горизонтальной оси, проходящей через точку О, расположенную между
грузами. Стержень удерживают в горизонтальном положении и отпускают без толчка. Найдите модуль силы
, с
которой груз
действует на стержень в момент, когда он проходит положение равновесия. Расстояние от точки
О до груза
равно
. Какие законы Вы используете для решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Невесомый стержень и тела и
образуют твёрдое тело (форма и размеры тела неизменны, расстояние между двумя
точками тела остается неизменным).
3. Изменение механической энергии твёрдого тела в ИСО равно работе Внешних непотенциальных сил. На твёрдое тело
действуют внешние силы:
со стороны оси, на которой вращается стержень и потенциальные силы
тяжести
и
. Работа силы
равна нулю так как трение отсутствует. Поэтому механическая энергия твёердого тела
сохраняется.
4. Искомая сила связана третьим законом Ньютона с силой
, с которой стержень действует на груз
:
.
5. Грузы отдельно можно считать материальными точками, описываем их движение с использованием второго закона Ньютона.
Решение
Рассмотрим положение, когда груз находится внизу. Пусть грузы движутся со скоростями
и
соответственно.
Расставим силы, действующие на тела:
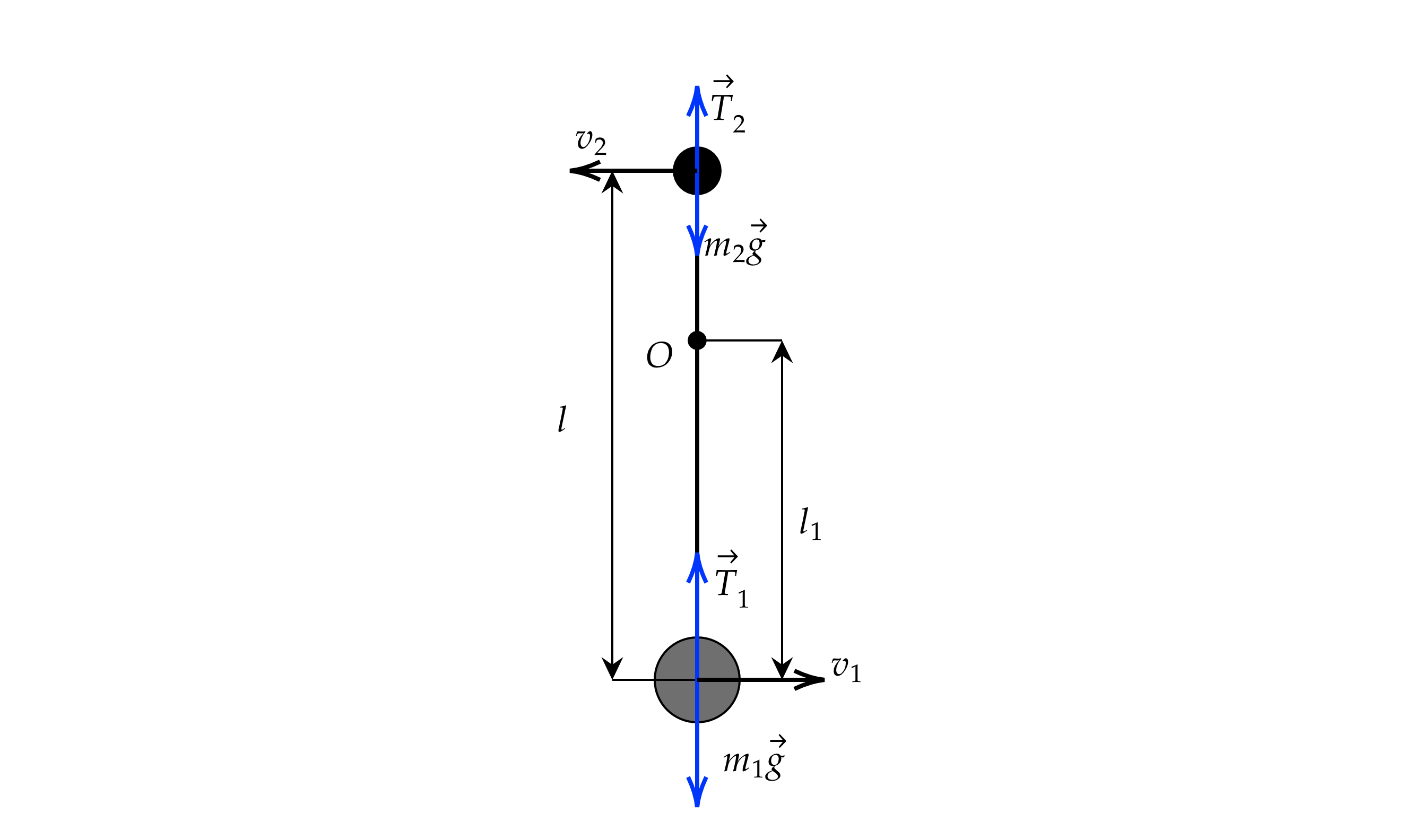
Здесь и
– реакции со стороны стержня. При этом по третьему закону Ньютона груз
действует на стержень с силой
по модулю, равной
.
Когда грузы покоятся, то их полная энергия равна нулю. В положении, изображенном на рисунке тела обладают кинетическими и
потенциальными энергиями, равнымы:
Запишем закон сохранения энергии:
Тела вращаются вокруг точки с одинаковой угловой скоростью, тогда следует равенство:
Отсюда:
Запишем (3) с учётом (1), (2), (4) и условий ,
,
:
При вращении груза создаётся центростремительное ускорение, направленное в центр и равное:
Спроецируем второй закон Ньютона для первого груза на вертикальную ось:
С учётом (5), (6) и условий ,
:
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обоснована возможность применения к системе тел модели абсолютно твёрдого тела
4. Обосновано применение второго и третьего законов Ньютона для описания движения тел
5. Обосновано применение закона сохранения энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения полной механической
энергии, второй закон Ньютона, формула центростремительного ускорения, формула связи линейных
скоростей);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений, использиемых в условии
задачи, и стандартных обозначений величин. используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения искомой величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности,
и проведены необходимые преобразования, но имеется один или несколько из следующих
недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/ вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
На горизонтальной поверхности неподвижно закреплена абсолютно гладкая полусфера радиусом м. С её верхней точки из
состояния покоя соскальзывает маленькое тело. В некоторой точке тело отрывается от сферы и летит свободно. Найдите скорость
тела в момент отрыва от сферы. Сопротивлением воздуха пренебречь. Какие законы Вы используете для решения задачи?
Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень горизонтальной поверхности.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
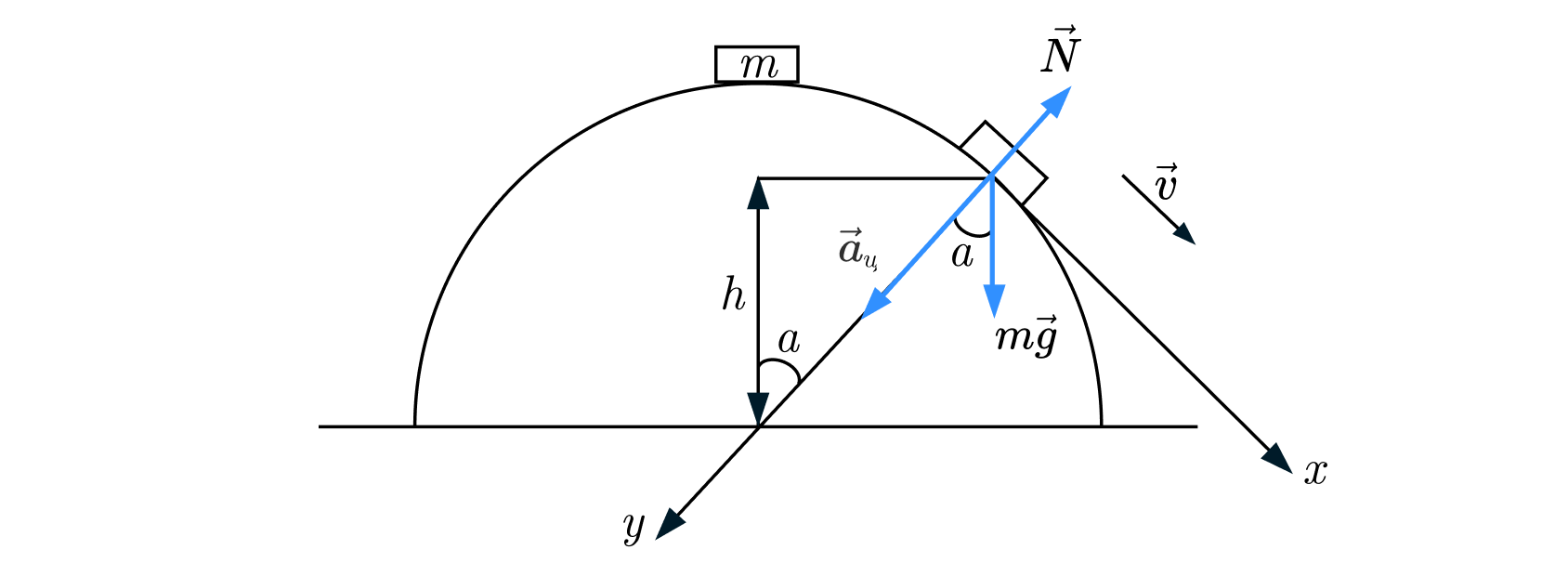
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести. Запишем второй закон Ньютона
где – масса тела,
– сила реакции опоры,
– центростремительное ускорение.
Так как , то с учетом формулы центростремительного ускорения
где
– скорость тела,
– радиус
полусферы.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Также запишем закон сохранения энергии
где – потенциальная энергия тела на высоте
,
– кинетическая энергия на высоте
,
–
потенциальная энергия на высоте
. Расписав все слагаемые по формулам получим
Подставим (1) в (2)
Критерии проверки
Критерий 1
1 балл ставится если
Верно обоснована возможность использования законов (закономерностей)
0 балл ставится если В обосновании возможности использования законов (закономерностей) допущена ошибка.
ИЛИ
Обоснование отсутствует
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае – закон сохранения
механической энергии; второй закон Ньютона для движения точки по окружности; формула
центростремительного ускорения; учтено, что в точке отрыва сила реакции опоры обращается в
нуль);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями);
IV) представлен правильный ответ с указанием единиц измерения физической величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования. Но имеются один или несколько из следующих
недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях / вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых
необходимо для решения данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
Сделаны только правильные рисунки, на которых построены изображения двух источников, с указанием хода лучей в линзе
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла
Ошибка.
Попробуйте повторить позже
Снаряд массой 4 кг, летящий со скоростью 400 м/с в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая – в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину 0,5 МДж. Найдите модуль скорости осколка, движущегося по направлению движения снаряда. Какие законы Вы используете для решения задачи? Обоснуйте их применение.
Источники:
Обоснование
Введем инерциальную систему отсчёта, связанную с Землёй, и направим ось Оx системы координат в направлении
начальной скорости движения снаряда. При описании движения снаряда и осколков используем модель материальной
точки. Для описания разрыва снаряда использован закон сохранения импульса системы тел. Он выполняется в
инерциальной системе отсчёта, если сумма внешних сил, приложенных к телам системы, равна нулю. В данном случае из-за
отсутствия сопротивления воздуха внешней силой является только сила тяжести , которая не равна нулю. Но этим
можно пренебречь, считая время разрыва снаряда малым. За малое время разрыва импульс каждого из осколков
меняется на конечную величину за счёт больших внутренних сил, разрывающих снаряд при взрыве. По сравнению
с этими большими силами конечная сила тяжести пренебрежимо мала. Так как время разрыва снаряда считаем
малым, то можно пренебречь и изменением потенциальной энергии снаряда и его осколков в поле тяжести в процессе
разрыва.
Решение
Кинетическая энергия тела находится по формуле:
где – масса тела,
– его скорость.
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии
|
|
где начальная скорость гранаты.
Выразим скорость второго осколка из второго уравнения.
Подставим в первое уравнение системы
Выразим :
Критерии проверки
Критерий 1
1 балл ставится если
Верно обоснована возможность использования законов (закономерностей). В данном случае: выбор ИСО, материальная точка, условия применения закона сохранения импульса и закона сохранения энергии
_________________________________________________________________________________________________________________________
В обосновании отсутствует один или несколько из элементов.
(ИЛИ)
В обосновании допущена ошибка.
(ИЛИ)
Обоснование отсутствует
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса, закон
сохранения энергии);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых вусловии
задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения физической величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования, но имеется один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
B необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения
и формулы, выражающие физические законы, применение которых необходимо для решения данной
задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
На гладкой горизонтальной плоскости находится длинная доска массой . По доске скользит шайба массой
кг.
Коэффициент трения между шайбой и доской
. В начальный момент времени скорость шайбы
м/с, а доска
покоится. В момент
с шайба перестает скользить по доске. Чему равна масса доски
? Обоснуйте применимость законов,
используемых для решения задачи.

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шайба поступательно, поэтому её можно считать материальной точкой.
3. Так как шайба является материальной точкой, то описывать её движение в ИСО будем, используя второй закон Ньютона.
4. Поскольку система является замкнутой и внешние силы на нее не действуют, применим закон сохранения импульса для описания взаимодействия тел
5. Поскольку действующие на шайбу силы постоянны, ускорение с которым она движется постоянно. Будем использовать формулы кинематики равноускоренного движения для описания движения шайбы
Решение
Расставим силы, действующие на шайбу при движении по доске.
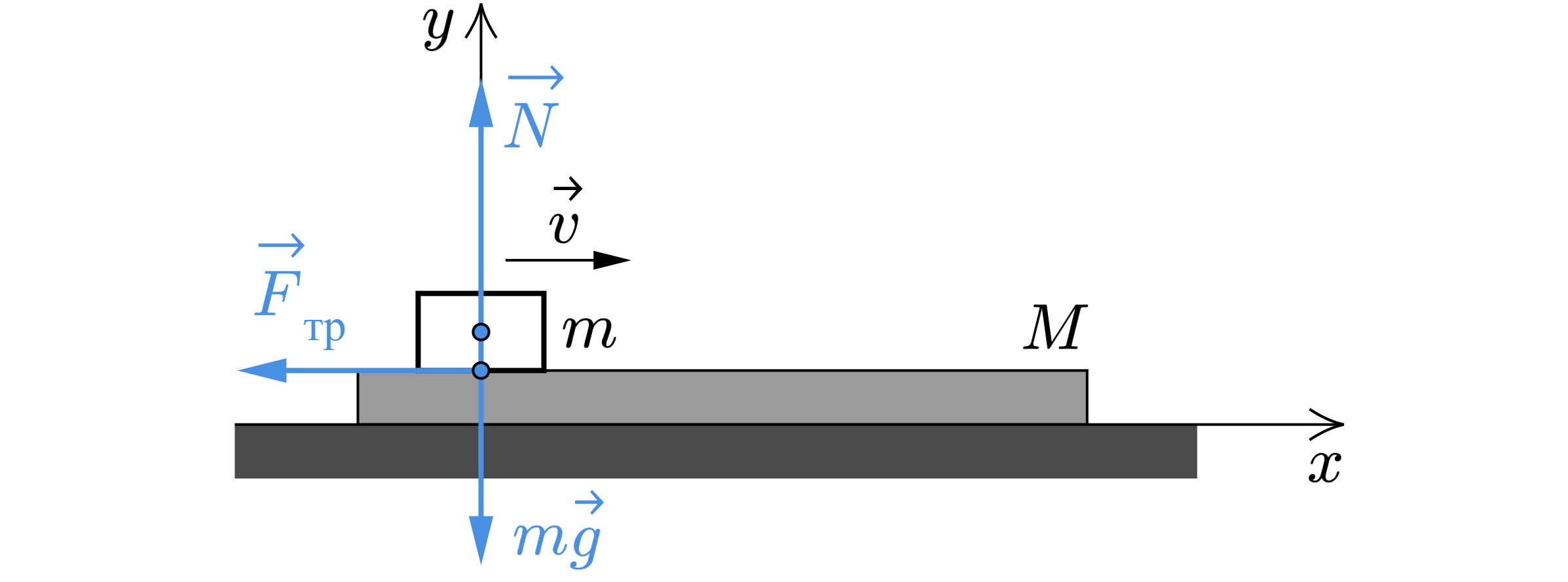
Движение шайбы прекратится в тот момент, когда скорость шайбы и доски будет одинакова. Запишем закон сохранения импульса:
где – скорость системы "шайба+доска".
Спроецируем на ось :
Запишем второй закон Ньютона:
где – сила трения скольжения,
– сила реакции доски,
– ускорение шайбы.
Сила трения скольжения равна:
Спроецируем второй закон Ньютона на вертикальную ось :
И на горизонтальную ось :
Тогда
Движение шайбы по доске является равноускоренным, значит, описывается уравнением:
Подставим (1) и (2) в (3)
Или
Отсюда
Ошибка.
Попробуйте повторить позже
На краю стола высотой м лежит пластилиновый шарик массой
г. На него со стороны стола налетает по
горизонтали другой пластилиновый шарик, имеющий скорость
м/с. Какой должна быть масса второго шарика, чтобы
точка приземления шариков на пол была дальше от стола, чем заданное расстояние
м? (Удар считать центральным.)
Какие законы Вы используете для решения задачи? Обоснуйте их применение.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем описывать тела моделью материальной точки.
3. Будем считать, что время соударения мало, и действие внешних сил во много раз меньше сил внутренних, поэтому момент соударения будем описывать с использованием закона сохранения импульса .
Решение
Закон сохранения импульса имеет вид
где – импульс шарика до столкновения,
– импульс системы после столкновения.
Импульс тела равен
где – масса тела,
– скорость тела.
Закон сохранения импульса в проекции на горизонтальную ось:
Найдём время падения из уравнения кинематики:
где – начальная скорость по вертикальной оси,
– начальная координата,
– проекция ускорения на ось
.
Так как во время падения , то
Так как горизонтальная составляющая скорости постоянна, то дальность полета равна:
Отсюда масса второго шарика :
Критерии проверки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение закона сохранения импульса
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохраненияимпульса, формулы
кинематики равноускоренного движения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)
И (ИЛИ)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
И (ИЛИ)
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Снаряд массой 2 кг разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения
снаряда, а другая – в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за
счёт энергии взрыва на величину . Модуль скорости осколка, движущегося по направлению движения снаряда, равен 900 м/с, а
модуль скорости второго осколка равен 100 м/с. Найдите величину
. Обоснуйте применимость законов, используемых для
решения задачи.
Обоснование
1) Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли.
2) Будем считать все тела материальными точками. Трением снаряда и осколков о воздух пренебрежём.
3) Поскольку время разрыва снаряда мало, импульсом внешних сил (сил тяжести) можно пренебречь, а значит, для решения задачи
можно воспользоваться законом сохранения импульса.
4) Так как при решении задачи мы пренебрегаем силой трения, то можно использовать закон сохранения энергии для снаряда с
учётом энергии разрыва.
Решение
Кинетическая энергия тела находится по формуле:
где – масса тела,
– его скорость.
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии
|
|
где начальная скорость гранаты.
Выразим начальную скорость гранаты из второго уравнения.
Подставим в первое уравнение системы
Выразим изменение кинетической энергии за счет взрыва
Критерии проверки
Критерий 1
1 балл ставится если
Верно обоснована возможность использования законов (закономерностей). В данном случае: выбор ИСО, материальная точка, условия применения закона сохранения импульса и закона сохранения энергии
_________________________________________________________________________________________________________________________
В обосновании отсутствует один или несколько из элементов.
(ИЛИ)
В обосновании допущена ошибка.
(ИЛИ)
Обоснование отсутствует
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса, закон
сохранения энергии);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением
обозначений констант, указанных в варианте КИМ, обозначений величин, используемых вусловии
задачи, и стандартных обозначений величин, используемых при написании физических
законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых
данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по
частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения физической величины
2 балла ставится если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены необходимые преобразования, но имеется один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.
И (ИЛИ)
B необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения
и формулы, выражающие физические законы, применение которых необходимо для решения данной
задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи
Во всех остальных случаях за задачу выставляется 0 баллов.
Ошибка.
Попробуйте повторить позже
Небольшое тело массой кг лежит на вершине гладкой полусферы радиусом
м. В тело попадает пуля массой
кг, летящая горизонтально со скоростью
м/с, и застревает в нём. Пренебрегая смещением тела за время удара,
определите высоту
, на которой это тело оторвётся от поверхности полусферы. Высота отсчитывается от основания
полусферы. Сопротивлением воздуха пренебречь. Обоснуйте применимость законов, используемых для решения
задачи.
Обоснование
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной. Тела можно считать материальными точками, так как их размеры пренебрежимо малы в условиях задачи.
2. При соударении для системы «пуля - тело» в ИСО выполняется закон сохранения импульса в проекциях на горизонтальную ось, так как внешние силы (сила тяжести и сила реакции опоры) вертикальны.
3. При движении составного тела от вершины полусферы выполняется закон сохранения механической энергии, так как полусфера гладкая, и работа силы реакции опоры равна нулю (эта сила перпендикулярна скорости тела).
4. В момент отрыва обращается в нуль сила реакции опоры .
5. Второй закон Ньютона выполняется в ИСО для модели материальной точки.
Решение
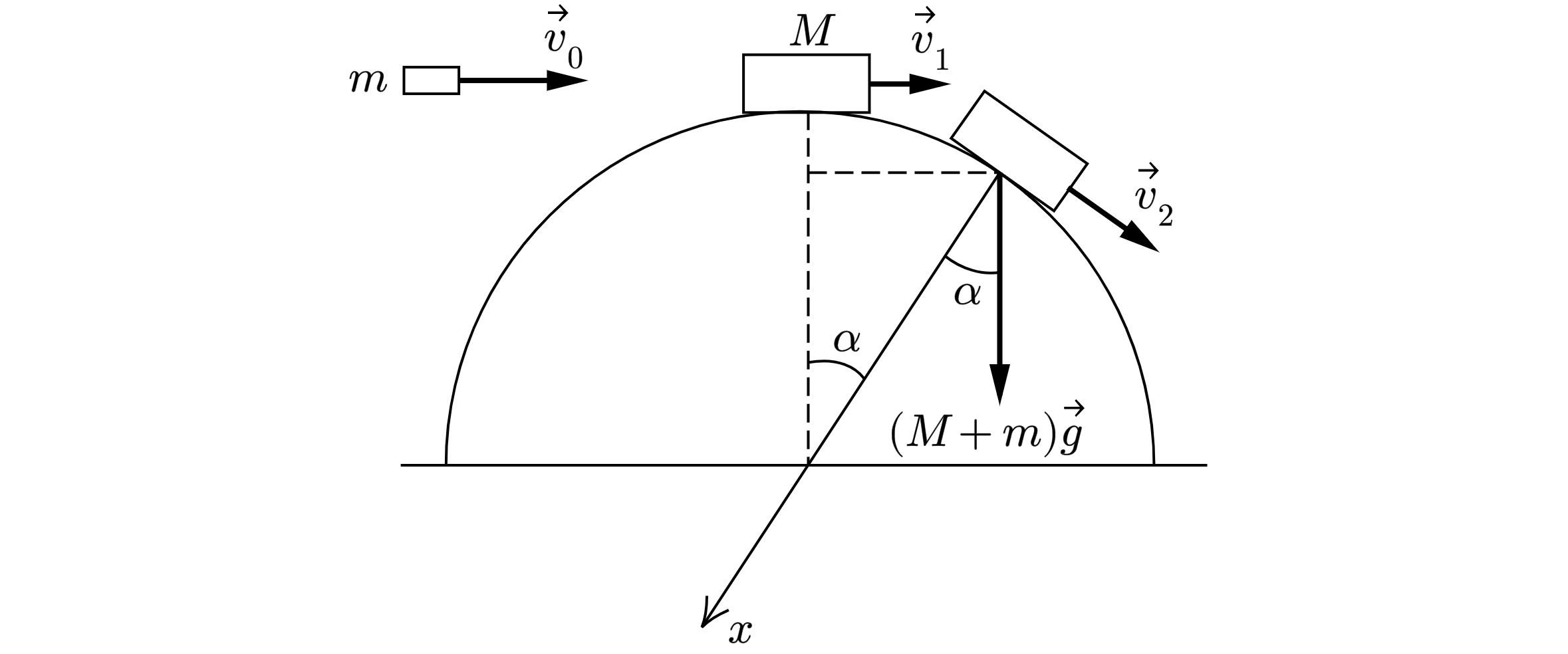
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести. Запишем второй закон Ньютона
где – сила реакции опоры,
– центростремительное ускорение Так как
, то с учетом формулы
центростремительного ускорения
где
– скорость составного тела,
– радиус полусферы.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Запишем закон сохранения импульса в момент, когда пуля касается бруска
где – импульс пули,
– импульс составного тела после столкновения,
– скорость после
столкновения.
Закон сохранения импульса на горизонтальную ось
Отсюда скорость после столкновения
Также запишем закон сохранения энергии
где – кинетическая энергия после столкновения(на высоте
),
– потенциальная
энергия тела на высоте
,
– кинетическая энергия на высоте
,
– потенциальная
энергия на высоте
. Расписав все слагаемые по формулам получим
Подставим (1), (2) в (3)
Отсюда искомая величина
Ошибка.
Попробуйте повторить позже
На горизонтальной поверхности неподвижно закреплена абсолютно гладкая полусфера радиусом м. С её верхней точки из
состояния покоя соскальзывает маленькое тело. В некоторой точке тело отрывается от сферы и летит свободно. Найдите скорость
тела в момент отрыва от сферы. Сопротивлением воздуха пренебречь. Обоснуйте применимость используемых законов к решению
задачи.
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень горизонтальной поверхности.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительным ускорением, направленным к центру окружности вращения.
Решение
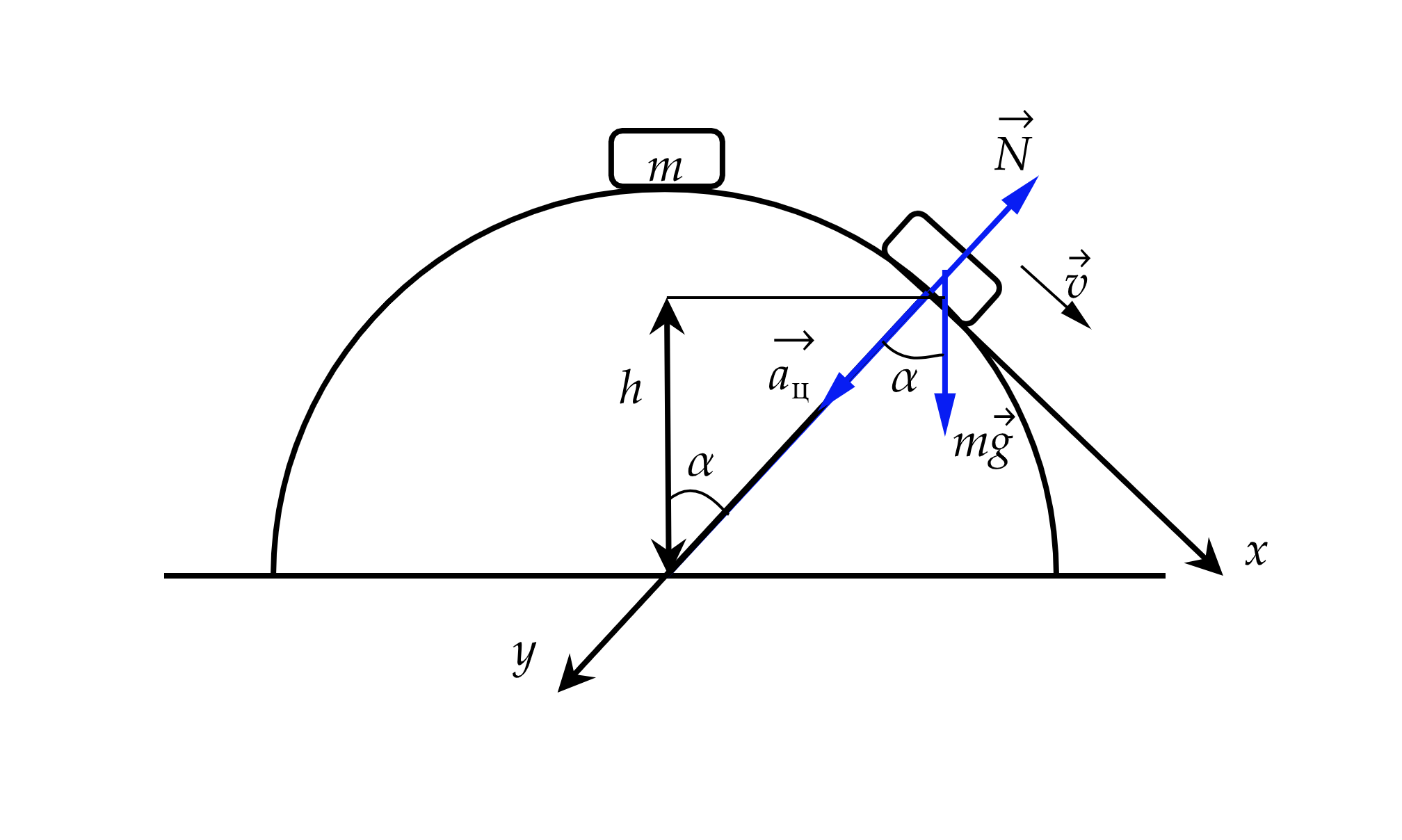
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой тяжести. Запишем второй закон Ньютона
где – масса тела,
– сила реакции опоры,
– центростремительное ускорение.
Так как , то с учетом формулы центростремительного ускорения
где
– скорость тела,
– радиус
полусферы.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Также запишем закон сохранения энергии
где – потенциальная энергия тела на высоте
,
– кинетическая энергия на высоте
,
–
потенциальная энергия на высоте
. Расписав все слагаемые по формулам получим
Подставим (1) в (2)
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность использования законов (закономерностей). В данном случае: введена инерциальная система отсчета, материальная точка, обосновано применение второго закон Ньютона, обосновано примененеи закона сохранения энергии, указан тип движения тела | 1 |
| В обосновании отсутствует один или несколько элементов | 0 |
| ИЛИ | |
| В обосновании допушена ошибка | |
| ИЛИ | |
| Обоснование отсутствует | |
| Критерий 2 | |
| I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: закон сохранения энергии, формула кинетической и потенциальной энергий, второй закон Ньютона, формула центростремительного ускорения); | 3 |
| II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); | |
| III) представлены необходимые математические преобразования и расчёты (подстановка числовых данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения физической величины | |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеется один или несколько из следующих недостатков. | 2 |
| Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. | |
| И (ИЛИ) | |
| В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты | |
| И (ИЛИ) | |
| В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. | |
| И (ИЛИ) | |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины) (В ответе обязательно указываются единицы измерений.) | |
| Представлены записи, соответствующие одному из следующих случаев. | 1 |
| Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. | |
| ИЛИ | |
| В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. | |
| ИЛИ | |
| В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. | |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
На противоположных концах тележки массы M, находящейся на гладкой горизонтальной поверхности, стоят два ученика
одинаковой массы каждый. Длина тележки
. Вначале система неподвижна. Один ученик бросает мяч, а другой ловит. Масса
мяча
. В процессе полета горизонтальная составляющая скорости мяча относительно поверхности, на которой находится
тележка, равна
.
1. Найдите скорость тележки после броска.
2. Найдите продолжительность полета мяча.
3. Найдите скорость тележки после того, как второй ученик поймает мяч.
Силу сопротивления воздуха считайте пренебрежимо малой.
(«Физтех», 2020, 10)
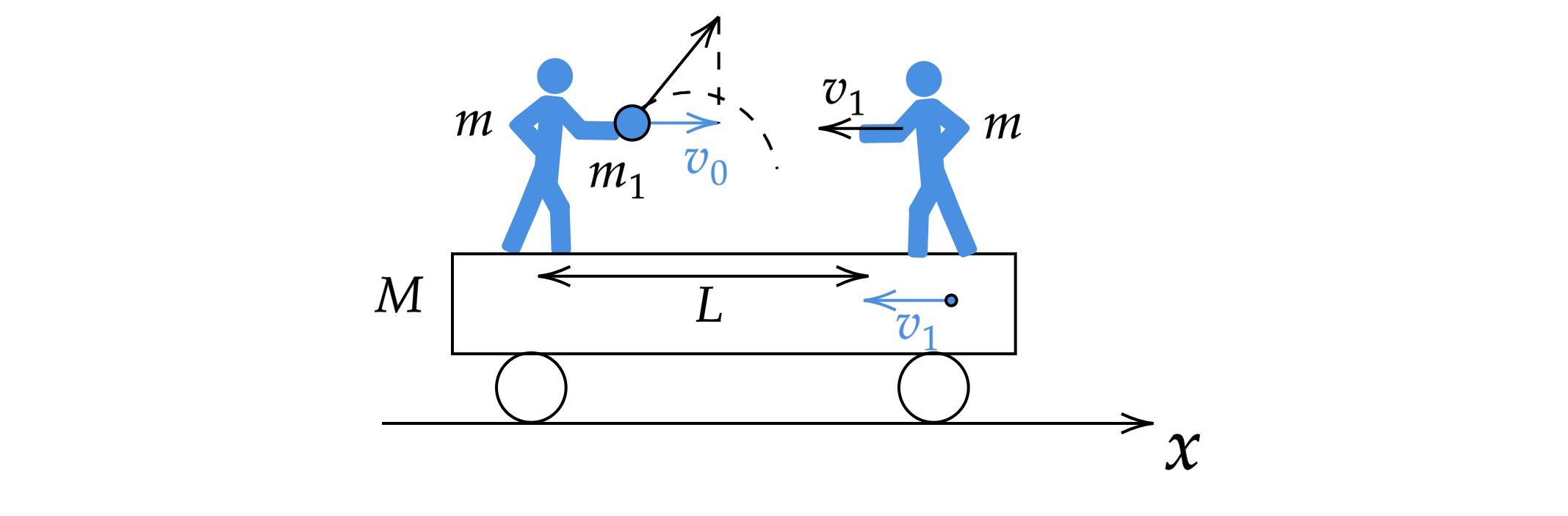
Так как мальчики стоят на тележки, то их скорость будет равна скорости тележки. Запишем закон сохранения импульса на ось
2. Так как тележка движется противоположно движению шарика, то
3. Пусть, когда второй мальчик поймает мячик скорость системы равна
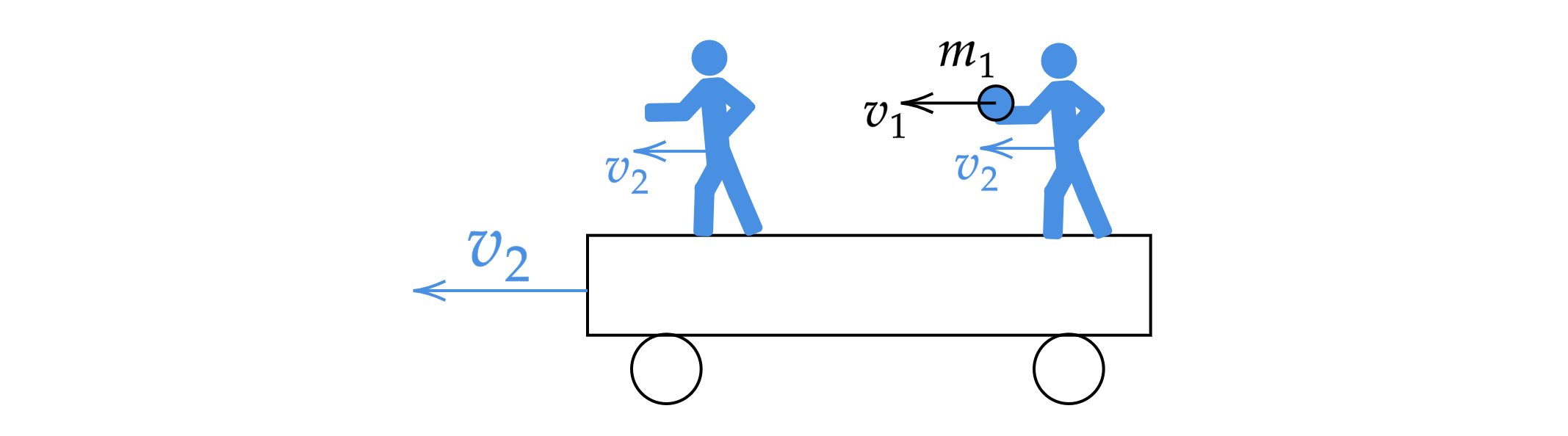
Запишем закон сохранения импульса
Ошибка.
Попробуйте повторить позже
На гладком горизонтальном столе покоятся два одинаковых кубика массой каждый. В центр левого кубика попадает пуля
массой
, летящая горизонтально со скоростью
, направленной вдоль линии, соединяющей центры кубиков. Пробив насквозь
левый кубик, пуля летит дальше со скоростью
, попадает в правый кубик и застревает в нем. Через какое время
после
попадания пули в левый кубик кубики столкнутся, если начальное расстояние между ними равно
? Размерами кубиков
пренебречь.
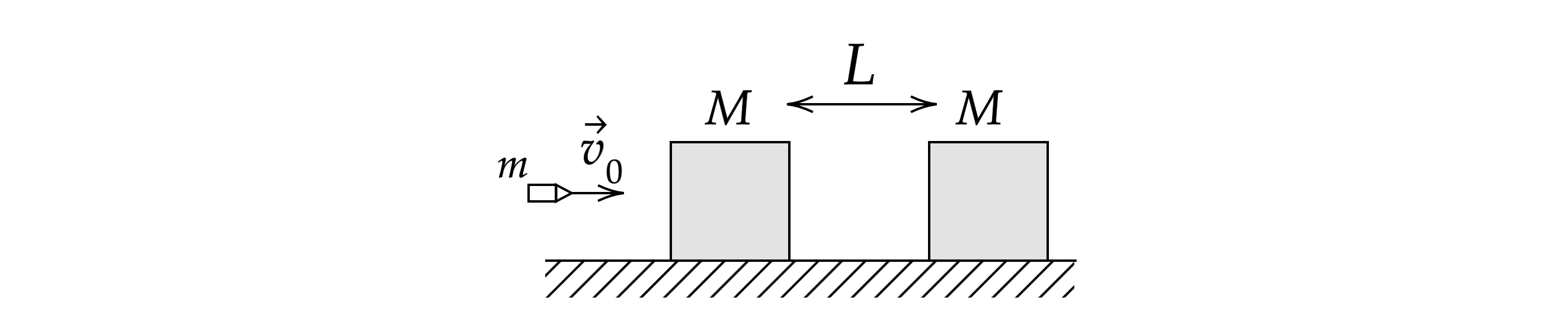
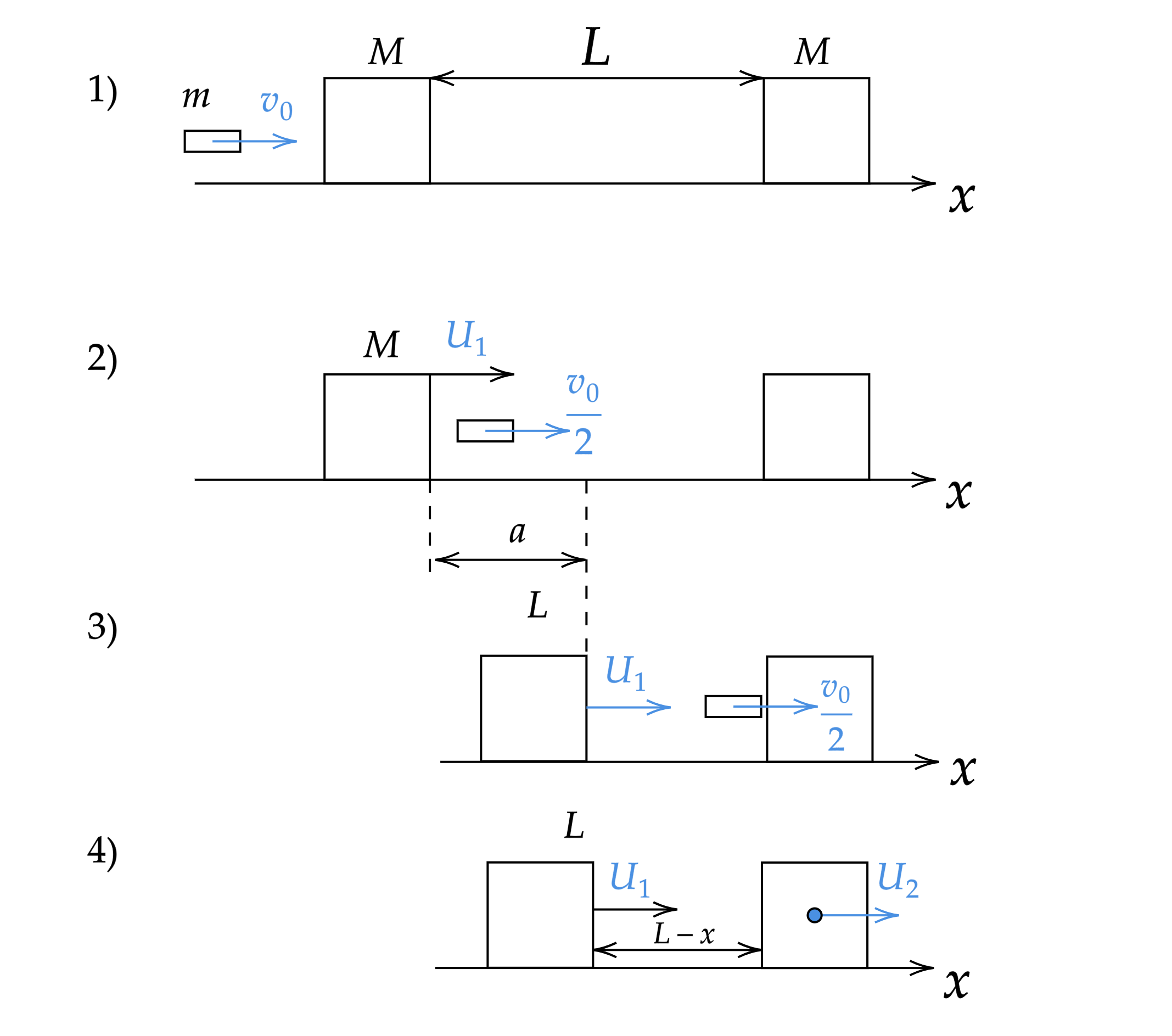
Запишем закон сохранения импульса на ось для 2) (пуля пробивает левый кубик)
Пуля долетит до второго бруска через
Тогда расстояние равно
Запишем также закон сохранения импульса на ось для 3) (пуля застревает в правом бруске)
При этом расстояние между брусками равно Тогда время, через которое левый брусок догонит правый из положения
4)
И искомое время



