Тема Алгебраические текстовые задачи

Задачи с неравенствами

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела алгебраические текстовые задачи

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#63739

На заводе имеются в достаточном количестве три сплава титана, алюминия и молибдена. Все сплавы с примесями. Процентное содержание компонентов в этих сплавах приведено в таблице.


	1	2	3

Молибден	$8%$	$3%$	$8%$

Титан	$36%$	$21%$	$6%$

Алюминий	$55%$	$76%$	$15%$

Из этих сплавов необходимо приготовить новый сплав, в котором алюминия должно быть не больше $38%$ , а молибдена - не меньше $5%$ . Какое наибольшее и какое наименьшее содержание титана (в процентах) может быть в этом сплаве?

Источники: ОММО-2023, номер 3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте сначала просто посчитаем. Пусть мы взяли x,y и 1-x-y первого, второго и третьего сплавов соответственно. Тогда как выглядят наши условия на нужный сплав и что мы хотим максимизировать/минимизировать?

Подсказка 2

Вы получили условия в виде неравенства для x и y, и выражение, которое надо максимизировать/минимизировать. Может быть, на плоскости эти неравенства будут нагляднее?)

Подсказка 3

Нам по факту надо найти макс/мин выражения 6+30x+15y. Понятно, что минимум будет в точке (0, 0). А чтобы найти максимум, можно заметить, что коэф при x больше, чем коэф при y....)

Показать ответ и решение

Первое решение.

Заметим, что как бы ни изготавливали новый сплав, содержание титана в нём будет не меньше минимального из содержаний титана в имеющихся сплавах. Поэтому содержание титана в любом изготовленном сплаве будет не менее $6%$ . С другой стороны, сплав 3 подходит под условия на содержание алюминия и молибдена. Значит, наименьшее содержание титана $− 6%$ .

Теперь найдём наибольшее содержание титана в таком сплаве. Заметим, что если при изготовлении нового сплава мы использовали сплав 2, то можно его заменить на сплав 1: от этого содержание алюминия уменьшится, а молибдена и титана - увеличится. Поэтому в сплаве с наибольшим содержанием титана не участвует сплав 2.

Сразу отметим, что тогда в таком сплаве будет $8%$ молибдена, т.е. он подходит под условие на молибден. В сплаве 1 титана больше, чем в сплаве 3 , но сплав 1 не подходит под условие на алюминий. Понятно, что чем меньше мы возьмём сплава 3, тем больше будет титана в изготовленном сплаве. Возьмём ровно столько, чтобы выполнилось условие на алюминий: $55x+15y = 38(x +y)(x$ и $y−$ масса сплава 1 и 3 соответственно), откуда $17x =23y$ , т.е. можно взять 23 части сплава 1 и 17 частей сплава 3. Тогда содержание титана в процентах будет

36⋅23+-6⋅17= 23,25 23+17

Второе решение.

Пусть взято $x,y$ и $1− x − y$ первого, второго и третьего сплава соответственно, причём $x ≥0,y ≥ 0,1− x− y ≥ 0$ . Тогда условия задачи можно записать так:

55x+ 76y+ 15(1− x− y)= 40x+ 61y+ 15 ≤38 8x+ 3y+8(1− x− y) =−5y +8≥ 5

Изобразим на координатной плоскости область (см. рисунок), удовлетворяющую системе неравенств

(|{ 40x+ 61y− 23≤ 0 −5y+ 3≥ 0 |( x≥ 0, y ≥ 0, x +y− 1≤ 0.

$PIC$

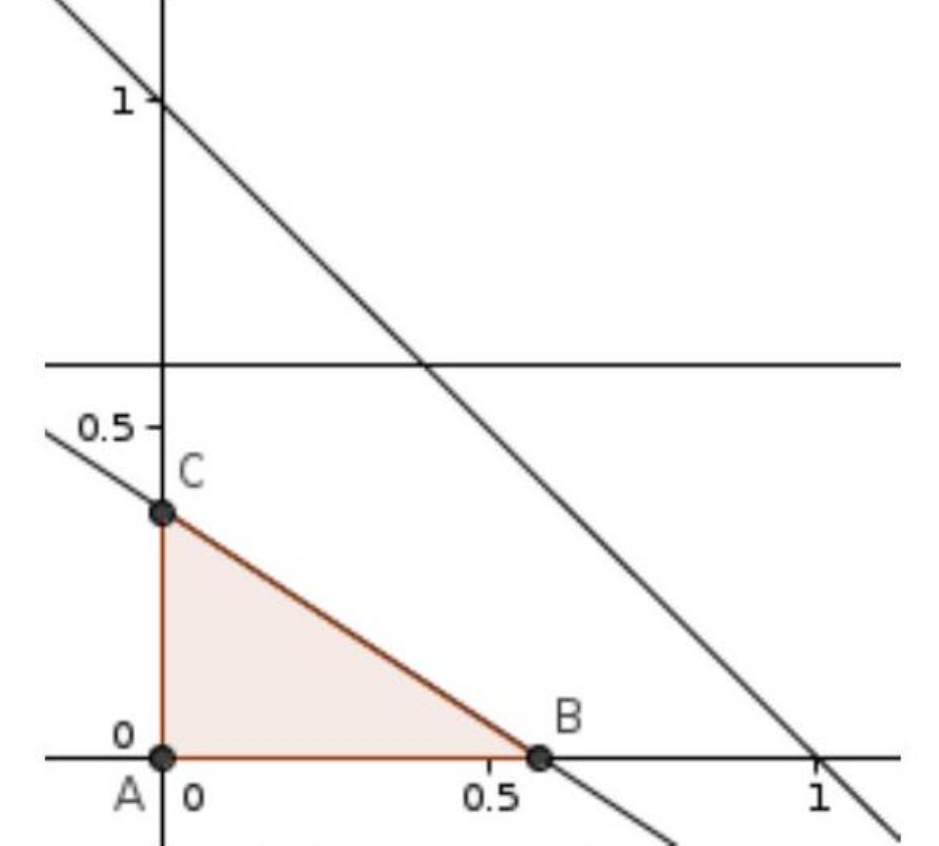
Процентное содержание титана $36x+ 21y+ 6(1− x− y) =6+ 30x+ 15y(∗)$ . Легко видеть, что минимум этого числа достигается в точке $A$ и равен 6 . Чтобы найти максимум, заметим, что абсцисса точки $B$ равна $23 1 40 > 2$ , а ордината точки $23 1 C− 61 < 2$ . При этом коэффициент при $x$ в $(∗)$ больше. Значит, значение в точке $B$ точно больше (мы большее число умножаем на большее число), и равно $23 6+ 30⋅40 = 23,25.$

Ответ:

наименьшее $6%$

наибольшее $23,25%$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68074

Петя и Вася пригласили одноклассников на свой день рожденья в дом Пети и посадили всех за круглый стол пить чай. Петя отметил для себя наименьшее число стульев, разделяющих его с каждым из приглашенных гостей, кроме Васи. Сложив полученные числа, он получил 60 . Найти число стульев за столом, если известно, что оно четное. Какое наименьшее число стульев разделяло Петю и Васю?

Источники: Росатом-2023, 11.1, Москва (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте попробуем для начала ввести удобные обозначения для количества людей между Петей и человеком. Заметим, что Петя считал наименьшие расстояния до людей на окружности. Тогда что особенного с подсчётом на ней? Можем ли мы просто пронумеровать подряд людей, и это будет правильно?

Подсказка 2

Верно, когда мы считаем наименьшее число на окружности, например, по часовой стрелке, то при переходе через середину это число уже не будет наименьшим, потому что мы могли пойти против часовой и получить меньшее число. Значит, мы нумеруем людей через подсчитанные расстояния Пети до середины, а потом в обратном порядке. Учитывая, что всего чётное число людей, найти сумму этих расстояний, включая Васю не составляет труда. Чтобы воспользоваться дальнейшим условием задачи, что хорошо ввести?

Подсказка 3

Да, можно ввести то, что спрашивают у нас в задаче. То есть пусть всего людей было 2n, а подсчитанное расстояние до Васи это y. Тогда мы понимаем как записывается то, что посчитал Петя и чему оно равно по условию. Также можно написать условие для расстояния до Васи, снова учитывая, что мы считаем его на окружности. У нас получилась система, решив которую для натурального n, мы получим ответы на задачу.

Показать ответ и решение

Пусть за столом стояло $2n$ стульев (т.е. за столом сидело всего $2n$ человек). На круге точками отмечены стулья. Числом рядом с точкой обозначено количество стульев, разделяющих Петю и человека, сидящего на этом стуле.

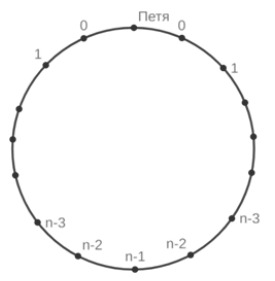
Тогда число стульев, посчитанных Петей, включая Васю, равно

2 2(1+ 2+ 3+ ⋅⋅⋅+(n− 2))+ (n− 1)= (n− 1)(n− 2)+(n− 1)=(n− 1)

Обозначим $K B$ число стульев, вычисленное для Васи. Тогда

({ 2 ({ 2 (|{ 2 (n − 1) − KB =60 ⇔ KB =(n− 1) − 60 ⇔ KB =√-(n − 1) − 60√- ( 0≤ KB ≤(n− 1) ( 0≤ (n − 1)2− 60≤ (n− 1) |( 1+ 60≤ n≤ 3+-2241

Учитывая, что $n∈ ℕ$ , $8< 1+ √60$ , $√--- 8< 3+--241< 10 2$ , получим единственное натуральное решение двойного неравенства: $n = 9$ . Тогда число стульев за столом равно $2n = 18$ , а количество стульев, разделяющих Петю и Васю, $KB = (n− 1)2− 60= 64− 60=$ $=4.$

Ответ: за столом 18 стульев, разделяло минимум 4

Ошибка.
Попробуйте повторить позже

Задача 3#69312

Во всем мире популярна игра в хоккей. Многое в игре зависит от вратаря. Для отработки навыков вратарей и обеспечения тренировочного процесса, который бы не зависел от других игроков, создали шайбомет. Автомат можно настроить так, чтобы он выбрасывал шайбы с заданной временной частотой, скоростью и под определенным углом.

Пусть линия ворот находится на расстоянии 25 м от центральной точки $O$ хоккейной площадки. Автомат установлен на расстоянии $d =16$ м от точки $O$ по направлению к воротам, скорость выброса шайбы равна $V0 = 20$ м/c. Броски производятся в плоскости, перпендикулярной поверхности льда и линии ворот. При этом для обеспечения безопасности траектория вылетающих шайб должна, с одной стороны, находиться не выше прямой линии, соединяющей центр ледовой площадки $O$ с точкой, находящейся в плоскости полета шайб, в плоскости ворот, и на расстоянии одного метра от поверхности льда, а с другой стороны — должна пересекать плоскость ворот по нисходящей ветви траектории.

$PIC$

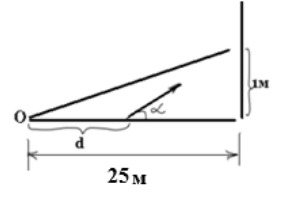
Определите максимально возможное значение тангенса угла, под которым могут вылетать шайбы из шайбомета, если траектория движения шайбы, рассматриваемой как материальная точка, в плоскости ее полета в системе координат с центром в $O$ и осью абсцисс, направленной вдоль поверхности льда, описывается уравнениями

({ x =d +V0tcosα ( gt2 y =V0tsinα − 2

Для упрощения вычислений можно считать, что ускорение свободного падения $g = 10$ м/c $2 .$

Источники: ШВБ-2023, 11.6 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1.

Вспоминаем уроки физики:) Так как переменная t у нас нигде не фигурирует, то хорошей идеей было бы от неё избавиться, подставив из первого уравнения во второе. Мы получим выражение вида y(x), в котором из тригонометрии будет находиться tg(a) и 1/cos²(a). Как бы нам получить только тангенс?

Подсказка 2.

1/cos²(a) = 1 + tg²(a). По условию наша шайба должна быть ниже условной линии на протяжении всего полёта. Тогда x * tg(b) <= y(x), где b - угол между осью площадки и линии, соединяющей центр поля с верхним концом ворот. Для каких x это должно выполняться?

Подсказка 3.

Поскольку траектория вылетающих шайб должна пересекать плоскость ворот по нисходящей ветви траектории, получили стандартное квадратичное неравенство, которое должно быть верно для всех x. Осталось записать условие неположительности дискриминанта и неотрицательности старшего члена, и оттуда найти наибольший возможный тангенс

Показать ответ и решение

Введем систему координат с центром в точке $O.$ Ось абсцисс направим к линии ворот.

Выразим время из первого уравнения системы и подставим во второе

( x − d )2 V0(x− d) g V0cosα g( x − d )2 y(x)= -V0cosα-sin α− -----2-----= (x− d)tgα − 2 V0cosα

2 y(x)=(x− d)tgα − g⋅ (x−2d)-⋅(1+ tg2α) 2 V0

Чтобы шайба была ниже условной линии для любого значения $x,$ требуется выполнение условия

x-≥ y(x) 25

x 25 − y(x)≥ 0

для любого $x ∈[16;25].$ Поскольку траектория вылетающих шайб должна пересекать плоскость ворот по нисходящей ветви траектории, то неравенство

2 -x − (x− d)tgα + g⋅ (x−2d)-⋅(1+ tg2α)≥ 0 25 2 V0

должно выполняться для всех $x.$

Перепишем неравенство в более удобном виде и учтем, что выполнение этого неравенства возможно лишь при неположительном дискриминанте.

g (x-− d)2 2 ( 1-) -d 2 ⋅ V20 ⋅(1+tg α)− (x− d) tgα− 25 + 25 ≥ 0

( )2 D = tgα −-1 − 4⋅-d ⋅ g⋅-12-⋅(1+ tg2α)≤0 25 25 2 V0

Подставляем $g = 10$ м/c $2$

( 1 )2 4d 2 tgα − 25 − 5V20 (1+tg α)≤ 0

′ ( ) ( )( ) D-= -1 − 1 −-4d2 -12 −-4d2 4 25 5V0 25 5V0

D′ -4d 1-- 4d-( -4d) 4d- 626 (-4d )2 4 = 5V20 ⋅252 + 5V02 1− 5V20 = 5V20 ⋅625 − 5V02

Подставляем $d= 16$ м, $V0 = 20$ м/с

( )2 ( ) D′ = 4⋅16-⋅ 626-− 4⋅16- = --4--- 626-− 4 = -4⋅606⋅2-- 4 5⋅400 625 5⋅400 25 ⋅252 5 252 ⋅25⋅5⋅2

Теперь посчитаем сам $tgα$

( 1 2 ∘ 1212) ( 121) 5± 2√121,2 tgα= 25 ±25⋅5 -10- ∕ 125- = ---121---

Значит, максимально возможное значение $tg α$ равно $√---- 5+2121121,2.$

Ответ:

$5-+2√121,2 121$

Ошибка.
Попробуйте повторить позже

Задача 4#82259

Десять положительных чисел выписали в строчку в порядке возрастания. Оказалось, что все разности между соседними числами равны, и что удвоенное второе по счету число больше четвертого по счету. Докажите, что упятеренное произведение всех чисел, стоящих на нечетных местах, больше произведения всех чисел, стоящих на четных местах.

Подсказки к задаче

Подсказка 1

Фактически нам дана арифметическая прогрессия. Каждое из 10 чисел выражается через разность прогрессии — разность двух соседних чисел и самое маленькое число. Обозначим самое маленькое число через a, а разность — x. Какое неравенство для a и x получается из условия?

Показать доказательство

Пусть разности равны $x,$ первое число равно $a.$ Тогда $2(a +x)> a+ 3x,$ откуда $a> x.$ Разобьем числа на пары соседних, в каждой паре $(a+ 2kx)∕(a +(2k+ 1)x)$ оценим отношение снизу как $(2k+1)∕(2k+ 2),$ поскольку при уменьшении $a$ до $x$ правильная дробь тоже уменьшится. Тогда отношение произведений оценивается снизу как $(1∕2)⋅(3∕4)⋅(5∕6)⋅(7∕8)⋅(9∕10)= 945∕3840> 1∕5.$

Ошибка.
Попробуйте повторить позже

Задача 5#33800

Молот тяжелее костюма, а костюм тяжелее, чем щит. Что тяжелее: молот или щит?

Показать ответ и решение

Обозначим массу молота через $a$ , массу костюма через $b$ , а массу щита через $c$ . Тогда у нас есть два условия: $a> b$ и $b> c$ . Таким образом, мы можем записать неравенство $a >b> c$ . Из этого следует, что $a> c$ , значит, молот тяжелее щита.

Ответ: Молот

Ошибка.
Попробуйте повторить позже

Задача 6#33801

Шесть карандашей легче пяти тетрадок, но тяжелее десяти ластиков. Что тяжелее: $2$ тетрадки или $3$ ластика?

Показать ответ и решение

Обозначим массу одного карандаша через $x$ , одной тетрадки через $y$ , одного ластика через $z$ . Перепишем тогда условия задачи: $6x< 5y$ , а также $6x> 10z$ . Тогда мы получаем неравенство $10z < 6x< 5y$ , или просто $10z < 5y$ . Поделим на $2$ , получим, что $2z < y$ . Значит, одна тетрадка тяжелее двух ластиков. Тогда две тетрадки тяжелее четырех ластиков, и тем более тяжелее трех ластиков.

Ответ: 2 тетрадки

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#33802

У $10$ инопланетян $44$ зуба. Докажите, что у каких-то двух инопланетян зубов поровну.

Показать ответ и решение

Предположим, что ни у каких двух инопланетян зубов не поровну. Это значит, что у любых двух инопланетян количество зубов различно. Упорядочим их по возрастанию количества зубов. Тогда у первого инопланетянина хотя бы $0$ зубов. У второго — уже хотя бы $1$ зуб. У третьего — хотя бы $2$ зуба, и так далее. Получается, что у инопланетян в сумме хотя бы $0+ 1+ 2+ ...+ 9=45$ зубов. Но по условию у них только $44$ зуба. Мы пришли к противоречию, значит, у каких-то двух инопланетян зубов поровну.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 8#33803

$7$ Камней Времени весят столько же, сколько весят $8$ Камней Души. Что легче: Камень Времени или Камень души?

Показать ответ и решение

Положим $7$ Камней Времени на левую чашу весов, а $8$ Камней Души на правую чашу. По условию, весы окажутся в равновесии. Если мы уберем с правой чаши один Камень Души, то правая чаша окажется легче. Значит, $7$ Камней Души легче, чем $7$ Камней Времени. Но тогда и один Камень Души легче, чем Камень Времени.

Ответ: Камень души

Ошибка.
Попробуйте повторить позже

Задача 9#33804

$3$ парты весят больше, чем $10$ стульев. Что тяжелее: парта или $3$ стула?

Показать ответ и решение

Нам нужно сравнить парту и $3$ стула. Умножим количество предметов на $3$ , тогда знак останется таким же. Получим, что надо сравнить $3$ парты и $9$ стульев. Так как $10$ стульев весят больше, чем $9$ стульев, и при этом $3$ парты весят больше, чем даже $10$ стульев, то $3$ парты тем более тяжелее, чем $9$ стульев. Значит, одна парта тяжелее трех стульев.

Ответ: Парта тяжелее

Ошибка.
Попробуйте повторить позже

Задача 10#33805

На очередной охоте $7$ смешариков сделали $20$ выстрелов. Докажите, что какие-то двое сделали поровну выстрелов.

Показать ответ и решение

Предположим, что никакие двое не сделали поровну выстрелов. Упорядочим смешариков по количеству выстрелов в порядке возрастания. У первого смешарика хотя бы $0$ выстрелов. У второго уже хотя бы $1$ выстрел. У третьего — хотя бы $2$ выстрела, и т. д., наконец, у седьмого смешарика хотя бы $6$ выстрелов. Получаем, что в сумме у них хотя бы $0+ 1+ 2+ ...+6 =21$ выстрел. Но по условию всего было сделано $20$ выстрелов. Мы пришли к противоречию, значит, какие-то двое все-таки сделали одинаковое число выстрелов.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 11#33806

Три школьные доски весят столько же, сколько четыре парты и два стула. Что тяжелее: доска или парта?

Показать ответ и решение

Положим на левую чашу весов три доски, а на правую — четыре парты и два стула. Тогда по условию весы окажутся в равновесии. Уберем с правой чаши два стула. Она станет легче, чем левая часть. Таким образом, $4$ парты легче, чем $3$ доски. Тем более $3$ парты легче, чем $3$ доски. Тогда, поделив на $3$ , получаем, что одна парта легче одной доски. Значит, доска тяжелее парты.

Ответ: Доска

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#33807

$24$ преподавателя “Школково” разделились на две компании: в одной $11$ человек, в том числе Дмитрий Алексеевич, а в другой $13$ человек, в том числе Максим Олегович. Первая компания выпила $5$ бутылок лимонада, причем все пили поровну. Вторая компания выпила $6$ бутылок лимонада, причем все тоже пили поровну. Кто выпил больше лимонада: Дмитрий Алексеевич или Максим Олегович?

Показать ответ и решение

Заметим, что в компании из $11$ человек люди выпили меньше, чем по пол бутылки лимонада на человека, так как $5⋅2= 10< 11$ . Добавим к ним еще одного человека и одну бутылку. Если бы эти двое выпили столько же, сколько остальная компания из $11$ человек, то в добавленной бутылке еще остался бы лимонад. И чтобы в итоге все $13$ человек выпили поровну, нужно разделить эти остатки между всеми $13$ людьми. Значит, люди в компании из $13$ человек выпили больше лимонада, чем люди в компании из $11$ человек. Таким образом, Максим Олегович выпил больше лимонада, чем Дмитрий Алексеевич.

Ответ: Максим Олегович

Ошибка.
Попробуйте повторить позже

Задача 13#33808

В межгалактическом буфете продаются только конфеты одного вида. Девять таких конфет стоят $11$ рублей с копейками, а тринадцать таких конфет стоят $15$ рублей с копейками. Сколько стоит одна конфета?

Показать ответ и решение

Будем переводить все цены в копейки. Первое условие означает, что $9$ конфет стоят не менее $1100$ копеек. Тогда одна конфета весит хотя бы $1100:9 >122$ копейки, то есть хотя бы $123$ копейки. Предположим, что она стоит больше, то есть хотя бы $124$ копейки. Тогда $13$ конфет стоят хотя бы $124⋅13=1612$ копеек, то есть уже больше $16$ рублей. Противоречие, значит, одна конфета стоит ровно $123$ копейки, или $1$ рубль и $23$ копейки.

Ответ: 1 рубль 23 копейки

Ошибка.
Попробуйте повторить позже

Задача 14#33809

Крош, Ёжик, Бараш и Муравей соревнуются в поедании бананов. На четверых они съели $70$ штук, причем каждый хоть что-то съел. Бараш съел больше, чем каждый из остальных. Крош и Ёжик съели вместе $45$ бананов. Сколько бананов съел Муравей?

Показать ответ и решение

Рассмотрим Кроша и Ёжика. Раз вдвоем они съели $45$ бананов, то хотя бы один из них съел не меньше $23$ штук. Действительно, иначе бы каждый из них съел не больше $22$ штук, и значит в сумме не больше $44$ бананов, противоречие.

Итак, кто-то из Кроша и Ёжика съел хотя бы $23$ банана. Бараш съел больше, значит, он съел хотя бы $24$ банана. Но на двоих с Муравьем они съели $70− 45=25$ бананов. Если бы Бараш съел больше $24$ бананов, то Муравью ничего бы не досталось. Значит, Бараш съел ровно $24$ банана, а Муравей — ровно $1$ банан.

Замечание. В итоге можно восстановить, что они съели $1$ , $22$ , $23$ и $24$ банана, но кто из Кроша и Ёжика съел $22$ , а кто — $23$ , определить нельзя.

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 15#33810

По результатам школьной олимпиады по математике награждали $8$ человек. Им подарили в сумме $84$ книги. Известно, что все они заняли разные места, причем те, кто заняли место выше, получили и книг больше. Кроме того, ребята, занявшие $7$ -е и $8$ -е места, получили в сумме больше книг, чем победитель олимпиады (то есть занявший $1$ -е место). Сколько книг получил участник, занявший $8$ -е место?

Показать ответ и решение

Обозначим количество книг, полученных участником, занявшим $8$ -е место, через $a$ . Тогда занявший $7$ -е место получил хотя бы $a+ 1$ книгу. Следующий — хотя бы $a+ 2$ книги, и т. д., занявший второе место получил хотя бы $a+6$ книг. Итого в сумме эти ребята получили хотя бы $a+(a+ 1)+(a+ 2)+...+ (a+ 6)= 7a+ 21$ книгу. Тогда победитель олимпиады получил не больше, чем $84− (7a+ 21) =63− 7a$ книг.

Также отметим, что победитель олимпиады получил хотя бы на $6$ книг больше, чем тот, кто занял $7$ -е место. Поэтому $a$ не меньше $7$ , иначе суммарное количество книг $7$ -го и $8$ -го не больше, чем количество книг у победителя олимпиады.

Если $a$ больше или равно $8$ , то получается, что у победителя олимпиады книг не больше, чем $63− 7 ⋅8 =7$ . Но в таком случае у $2$ -го места книг хотя бы $8+ 6= 14$ , что больше, чем у победителя. Этого быть не может, значит, $a$ не больше, чем $7$ . До этого мы также получили, что $a$ не меньше $7$ , значит, $a= 7$ . Именно это количество, то есть количество книг, полученных $8$ -м местом, нас и просили найти.

Ответ: 7

Ошибка.
Попробуйте повторить позже

Задача 16#34096

Показать ответ и решение

Ответ: 1

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#34097

В волшебной стране в ходу только купюры $63$ тугрика и $350$ тугриков. Известно, что самый дешевый предмет, который там можно купить в магазине — это iPhone 12 Pro. Какое наименьшее (разумеется, положительное) число тугриков может стоить айфон, если цену можно заплатить только имеющимися в ходу купюрами, получив при этом, разумеется, сдачу?

Показать ответ и решение

Сначала приведем пример, когда айфон может стоить $7$ тургиков. Для этого заплатим $2$ купюры по $350$ тугриков, получив в виде сдачи $11$ купюр по $63$ тугрика. Таким образом, стоимость будет равна $2⋅350 − 63⋅11= 7$ тугриков.

Теперь докажем, что меньше $7$ тугриков айфон стоить не может. Заметим, что и $63$ , и $350$ делятся на $7$ . Поэтому любая сумма или разность, полученная этими купюрами, также будет делиться на $7$ . Учитывая, что цена положительна, меньше $7$ тугриков она быть не может.

Ответ: 7 тугриков

Ошибка.
Попробуйте повторить позже

Задача 18#34098

Участнику телевикторины задают несколько вопросов. За каждый правильный ответ он получает $25$ долларов, а за неправильный — теряет $15$ долларов. Дональд завершил участие в телевикторине с минимальным возможных положительным заработком. Сколько заработал Дональд?

Показать ответ и решение

Заметим, что и 15, и 25 делится на 5, значит, и сумма, которая может быть у Дональда кратна 5. Минимальной положительное число, кратное 5, — это 5. Построим пример: пусть Дональд ответит 2 раза правильно и 3 раза неправильно, так он получит ровно $25+ 25− 15− 15− 15 =5$ долларов.

Ответ: 5

Ошибка.
Попробуйте повторить позже

Задача 19#34099

Класс из $10$ человек отправился собирать шишки. Все собрали разное количество шишек, а меньше всех собрал Вова — всего 4 шишки. Вернувшись в класс, дети насчитали в сумме $84$ шишки. Докажите, что по дороге была потеряна хотя бы одна шишка.

Показать ответ и решение

Так как Вова собрал 4 шишки, то второй по количеству шишек собрал хотя бы 5 шишек, аналогично третий собрал хотя бы 6, ..., 10-й собрал хотя бы $10+ 4− 1 =13$ . Значит, всего собрали хотя бы $4+ 5+ ...+ 13= (4+13)+ (5+ 12)+...+ (8+9)= 17⋅5= 85$ , а насчитали всего 84. Следовательно, была потеряна хотя бы одна шишка.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 20#34100

Какая наименьшая сумма цифр может быть у числа, кратного $69$ ?

Показать ответ и решение

Заметим, что $69 =3 ⋅23$ , значит, наше число обязательно кратно 3 => его сумма цифр тоже кратна 3, следовательно, хотя бы 3. Такое число с сумой цифр 3 действительно существует — $69⋅29= 2001$ .

Ответ: 3

Предыдущий раздел

Следующий раздел