Закл (финал) 9 класс
Ошибка.
Попробуйте повторить позже
Рассмотрим все 100-значные числа, делящиеся на 19.
Докажите, что количество таких чисел, не содержащих цифр 4,5 и 6, равно количеству таких чисел, не содержащих цифр 1, 4 и 7.
Источники:
Каждому остатку от деления на 19 сопоставим остаток
такой, что
Заметим, что остаткам сопоставлены остатки
соответственно. Более того, по остатку
восстанавливается
остаток
такой, что
и
(из аналогичных соображений).
Обозначим теперь через множество чисел из условия, не содержащих цифр
, а через
— множество таких чисел, не
содержащих
. Каждому числу
сопоставим число
. Заметим, что
— цифра
(причём
), так что получилось 100 -значное число. Кроме того,
так что делится на 19 и
. Поскольку разным числам из
соответствуют разные числа из
, количество чисел в
не
меньше, чем в
.
Наконец, каждому числу соответствует число
, которое по аналогичным причинам лежит
в
. Отсюда следует, что количества чисел в
и
равны.
Ошибка.
Попробуйте повторить позже
Биссектрисы треугольника пересекаются в точке
, внешние биссектрисы его углов
и
пересекаются в точке
. Окружность
с центром в точке
проходит через точку
и касается прямой
в точке
Окружность
с центром в точке
проходит
через точку
и касается прямой
в точке
Отрезки
и
пересекаются в точке
Найдите отношение
.
Источники:
Первое решение.
Проведём в окружности диаметр
, а в окружности
диаметр
. Заметим, что
, поскольку
внутренняя и внешняя биссектриса угла перпендикулярны. Следовательно, точка
лежит на
, а точка
- на
.
![]()
Кроме того, , поскольку
касается
в точке
, поэтому
. Аналогично,
. Итого, четырёхугольник
- параллелограмм, пусть его диагонали пересекаются в точке
. Тогда
, а отрезок
- средняя линия
треугольника
, поэтому точка
середина отрезка
. Таким образом,
, откуда следует, что
.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Обозначим через середину дуги
описанной окружности
треугольника
, а через
середину другой
её дуги
. Пусть луч
вторично пересекает
в точке
. Поскольку
- диаметр окружности
, то
.
По лемме о трезубце — середина отрезка
. Поскольку
и
, то
Продлим луч до пересечения с
в точке
.
![]()
Так как внешний для треугольника
, а также четырёхугольник
- вписанный, мы получаем, что
, поэтому окружность
касается прямой
в точке
. Также эта
окружность проходит через
, следовательно, это и есть окружность
. Аналогично, окружность
описана около треугольника
.
Значит, IP - общая хорда окружностей и
, а тогда
серединный перпендикуляр к отрезку
. Поскольку к тому же
, мы получаем, что
проходит через середину отрезка
, то есть
, а тогда
.
Ошибка.
Попробуйте повторить позже
Для какого наименьшего натурального числа существуют целые числа
и
такие, что квадратный трёхчлен
имеет два
различных положительных корня, не превосходящих
Источники:
Первое решение. Докажем, что Заметим, что если
—корень трёхчлена
то
—корень трёхчлена
Поэтому в задаче нужно найти наименьшее натуральное
для которого корни
и
некоторого трёхчлена
(с целыми
и
) больше
Поскольку
и
положительны и
(по теореме Виета), имеем
Если то
Поскольку меньший корень не меньше
больший корень не меньше
а тогда
Если же
то
В обоих случаях требуемая оценка
доказана.
Осталось заметить, что трёхчлен имеет корни
и
поэтому
подходит.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Положим для краткости Пусть
и
— два различных корня трёхчлена
причём
Тогда число
отрицательно, а число
положительно. Более того, имеем
откуда
Поскольку корни различны, дискриминант положителен. Следовательно,
и, значит,
Поэтому
Пусть
где
— натуральное число.
Предположим, что Тогда
и
Стало быть,
и, значит, Следовательно,
и
Это противоречие показывает, что
Если же то при
и
трёхчлен имеет корни
и
Ошибка.
Попробуйте повторить позже
Натуральные числа и
таковы, что
делится на
Докажите, что найдутся натуральные
и
такие, что
Заметим, что из равенства следует равенство
Поэтому для решения задачи достаточно найти
такое натуральное
что число
раскладывается в произведение двух натуральных чисел
и
больших
(тогда можно положить
и
Согласно условию,
для некоторых простого
и натурального
Если то в силу разложения
в качестве
можно взять число
Также, если число
составное,
то
при
тогда снова можно положить
так как
В оставшемся случае имеем при некоторых простом
Если
то
при некотором положительном
и натуральном
Тогда число
делится на а частное от деления больше
поскольку
Поэтому можно положить
Наконец, если то
причём
по условию. Тогда
где обе скобки
больше
в этом случае работает
Ошибка.
Попробуйте повторить позже
При каком наименьшем натуральном существуют такие целые
что квадратный трехчлен
имеет хотя бы один целый корень?
Источники:
При можно положить
и
; тогда трёхчлен из условия принимает вид
и имеет
два целых корня:
и
Осталось показать, что это — наименьшее возможное значение
Пусть числа удовлетворяют условию задачи; тогда делённый на
дискриминант квадратного трёхчлена из условия
должен быть полным квадратом. Он равен
Тогда число нечётно и является квадратом, поэтому оно даёт остаток
при делении на
Перепишем равенство выше в виде
и рассмотрим его по модулю Нетрудно проверить, что четвёртые степени целых чисел дают лишь остатки
и
при делении на
то есть правая часть равенства даёт остаток
или
Левая же часть сравнима с
где
— количество нечётных чисел среди
Значит,
При
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
равны. На сторонах
и
нашлись соответственно точки
и
такие, что
и
Пусть
— середина отрезка
а
— точка пересечения высот треугольника
Докажите, что
прямые
и
перпендикулярны.
Источники:
.png)
Выберем точки и
так, что точки
и
— середины отрезков
и
соответственно. Поскольку
и
отрезок
является средней линией в треугольнике
то есть
— середина
Поскольку четырехугольник является параллелограммом верно, что
то есть четырехугольник
вписан. При гомотетии с коэффициентом
с центром в
точки
переходят в точки
соответственно, то есть
четырехугольник
вписан.
По теореме Монжа из этого следует, что перпендикуляры из на
из
на
и из
на
пересекаются в одной точке.
Но первые два перпендикуляра пересекаются в точке
значит,
Ошибка.
Попробуйте повторить позже
Пусть — целые неотрицательные числа, а
— наименьшее из них. Докажите, что
(Как обычно, через обозначается целая часть числа
то есть наибольшее целое число, не превосходящее
)
Источники:
Положим . Тогда
а поскольку числа
целые, имеем
Если мы теперь покажем,
что
то правая часть доказываемого неравенства не будет превосходить что и требовалось.
Пусть для определенности Оценим подкоренное выражение в левой части доказываемого неравенства:
Квадрат правой части доказываемого неравенства равен
Сравнивая эти выражения, видим, что достаточно показать, что
Но при любых верно неравенство
При этом в правой части стоит
слагаемых такого вида. Оценивая
из них числом
а остальные
— числом
получаем требуемое.
Ошибка.
Попробуйте повторить позже
В карточной игре каждой карте сопоставлено числовое значение от до
причем каждая карта бьет меньшую, за одним исключением:
бьет
Игрок знает, что перед ним лежат рубашками вверх
карт с различными значениями. Крупье, знающий порядок этих
карт, может про любую пару карт сообщить игроку, какая из них какую бьет. Докажите, что крупье может сделать сто таких сообщений,
чтобы после этого игрок смог точно узнать значение каждой карты.
Источники:
Обозначим через карту значения
Выберем произвольное число Пусть крупье сообщит, какая карта бьёт другую, в парах
а также
во всех парах вида
при
Всего он сделает
сообщений.
Покажем, что по этим данным игрок может восстановить значения всех карт. Он может рассуждать так. Из того, что карты
бьют друг друга по циклу, следует, что одна из них имеет значение
а следующая по циклу — значение
Но, кроме карт этого цикла,
карту
бьёт карта
а карта
бьёт карту
Значит,
не может иметь значение
или
то есть значения
и
имеют карты
и
соответственно.
Наконец, среди оставшихся карт в любой паре карта с большим значением бьёт другую. Поскольку нам известно, что
каждая
бьёт
при
отсюда следует, что каждая
имеет значение
Ошибка.
Попробуйте повторить позже
Существует ли такая бесконечная возрастающая последовательность натуральных чисел, что сумма любых двух различных
членов последовательности взаимно проста с суммой любых трёх различных членов последовательности?
Источники:
Построим пример такой последовательности. Положим Для того, чтобы показать, что она удовлетворяет
требованиям, нам придётся эти требования несколько усилить. Будем говорить, что пара (тройка) чисел хорошая, если все её элементы,
отличные от единицы, различны (а единица может встретиться в ней несколько раз). Докажем следующее утверждение, из которого будет
следовать, что построенная последовательность — требуемая.
Пусть и
— хорошие пара и тройка элементов последовательности. Тогда НОД
НОД
Доказательство проведём индукцией по наибольшему индексу среди
и
Если
утверждение тривиально. Для
перехода предположим, что
Число
лежит либо только в паре
либо только в тройке
либо в
обеих.
Случай Пусть
— только элемент пары; скажем,
Тогда, поскольку
число
делится на
то есть НОД
НОД
НОД
по предположению индукции.
Случай Пусть
— только элемент тройки; скажем,
Аналогично,
делится на
так что
НОД
НОД
по предположению индукции.
Случай Пусть
— элемент и пары, и тройки; скажем,
Тогда
делится на
так что
НОД
НОД
НОД
НОД
по предположению индукции. Переход индукции доказан.
Да, существует
Ошибка.
Попробуйте повторить позже
Дана равнобокая трапеция с основаниями
и
Окружность
проходит через вершины
и
и вторично пересекает
сторону
и диагональ
в точках
и
соответственно. Касательная, проведенная к окружности
в точке
пересекает луч
в точке
Докажите, что точки
и
лежат на одной прямой.
Источники:
Поскольку а прямая
касается окружности
имеем
Следовательно,
то есть четырёхугольник
— вписанный.
Значит,
где последние два равенства следуют из того, что трапеция равнобокая, а четырёхугольник
вписан в
Таким
образом,
поэтому точки
и
лежат на одной прямой.
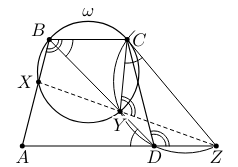
Ошибка.
Попробуйте повторить позже
В стране некоторые пары городов соединены односторонними прямыми авиарейсами (между любыми двумя городами есть не более одного
рейса). Скажем, что город доступен для города
если из
можно долететь в
возможно, с пересадками. Известно, что для
любых двух городов
и
существует город
для которого и
и
доступны. Докажите, что существует город, для которого
доступны все города страны. (Считается, что город доступен для себя.)
Источники:
Выберем город любой с наибольшим числом доступных городов. Предположим, что город
не доступен для
Тогда для
некоторого города
доступны оба города
и
Но тогда для
доступны все города, доступные для
и еще
город
то есть большее количество городов, чем для
Это противоречит выбору
значит, для
доступны все
города.
Ошибка.
Попробуйте повторить позже
Сумма положительных чисел равна
Докажите неравенство:
Домножив доказываемое неравенство на получим
Поскольку неравенство симметричное, можно считать, что По неравенству о средних для чисел
и
имеем
Следовательно, Значит, для доказательства (*) достаточно показать, что
После раскрытия скобок и приведения подобных слагаемых остаётся неравенство
которое является суммой двух очевидных неравенств и
Ошибка.
Попробуйте повторить позже
Остроугольный треугольник вписан в окружность
. Пусть
- точка пересечения его медиан, а
- высота этого
треугольника. Луч
пересекает
в точке
. Докажите, что окружность, описанная около треугольника
, касается
.
Источники:
Проведем серединный перпендикуляр к Пусть он пересекает луч
в точке
, а
в точке
. Тогда
Также проведем прямую, параллельную , через точку
. Пусть она пересекает
в точке
, а
— проекция точки
на
. Тогда
и
. Следовательно
— середина
.
.png)
Отметим точку такую, что
. Тогда
в силу подобия треугольников
и
. Кроме того, проецируя
на
получаем
. Следовательно,
по двум катетам. А значит,
—
равнобедренная трапеция и
лежит на окружности, описанной около
и
Следовательно,
— касательная к окружности, описанной около треугольника
Ошибка.
Попробуйте повторить позже
Числа и
таковы, что каждый из двух квадратных трёхчленов
и
имеет по два различных корня,
а произведение этих трёхчленов имеет ровно три различных корня. Найдите все возможные значения суммы этих трёх
корней.
Источники:
Если каждый трёхчлен имеет два различных корня, а их произведение — три различных, то эти трёхчлены имеют ровно один общий корень.
Значит, его имеет их разность . Отметим, что
иначе трёхчлены совпадут, равно как и их оба корня. Таким образом,
их общий корень равен
. При подстановке в оба трёхчлена получим
. Также по теореме Виета понятно, что первый трёхчлен
имеет корень
, а второй —
, тогда искомая сумма равна
.
Ошибка.
Попробуйте повторить позже
Натуральные числа и
большие
таковы, что
Какое наименьшее значение может принимать дробь
Источники:
Оценка. Заметим, что значит,
Но
и
– целые числа, поэтому
Следовательно,
Стало быть, то есть
Пример. Оценка достигается при
Ошибка.
Попробуйте повторить позже
Трапеция с основаниями
и
вписана в окружность
Окружность
проходит через точки
и
пересекает отрезки
в точках
соответственно. Точки
и
симметричны точкам
и
относительно середин отрезков
и
соответственно. Докажите, что точки
и
лежат на одной
окружности.
Четырехугольник вписан в окружность только тогда, когда произведение длин отрезков секущиx
и
равны.
Точки и
симметричны точкам
и
относительно середин отрезков
и
соответственно, следовательно,
и
то есть достаточно проверить равенство
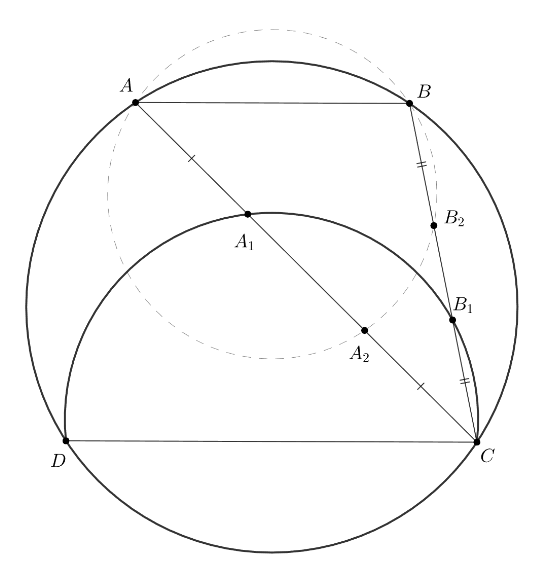
Левая и правая часть равны степеням точек и
относительно окружности
соответственно, и равны, поскольку
точки
симметричны относительно серединного перпендикуляра к отрезку
а значит, равноудалены от центра
Ошибка.
Попробуйте повторить позже
На доске написали попарно различных натуральных чисел
Затем под каждым числом
написали число
полученное прибавлением к
наибольшего общего делителя остальных
исходных чисел. Какое наименьшее количество попарно
различных чисел может быть среди
Источники:
Если положить и
при
то
так что среди чисел
будет не больше
различных.
Осталось доказать, что среди чисел
всегда найдутся
различных чисел.
Без ограничения общности можно считать, что Пусть
— наибольший общий делитель всех
исходных чисел,
кроме
тогда
Пусть
— наибольшее из чисел
Тогда при
числа
делятся на
Следовательно, при
и
разность
также делится на
Поскольку она положительна,
Поэтому
откуда Итак, мы установили, что
при
Стало быть, все
чисел
при
различны.
Ошибка.
Попробуйте повторить позже
Положительные числа таковы, что
и
Докажите, что какие-либо
два из чисел
отличаются больше, чем на
Источники:
Перемножив равенство
и неравенство
получим неравенство
Возведем теперь в квадрат равенство
Получим
Вычитая из неравенства равенство
получаем
или
Предположим теперь, что любые два числа отличаются не больше, чем на Тогда квадрат их разности не больше
и из
получаем неравенство
Но, если вычесть из квадрата равенства равенство
получится равенство
что противоречит Значит, найдутся два числа, отличающиеся больше, чем на
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник . Окружность, проходящая через вершину
и центр
его описанной окружности, вторично
пересекает стороны
и
в точках
и
соответственно. Докажите, что точка пересечения высот треугольника
лежит на
прямой
.
Источники:
Обозначим Тогда
Поскольку четырёхугольник
вписан,
и
Пусть
— высота треугольника
а
— точка пересечения прямых
и
Без ограничения
общности можно считать, точка
лежит на луче
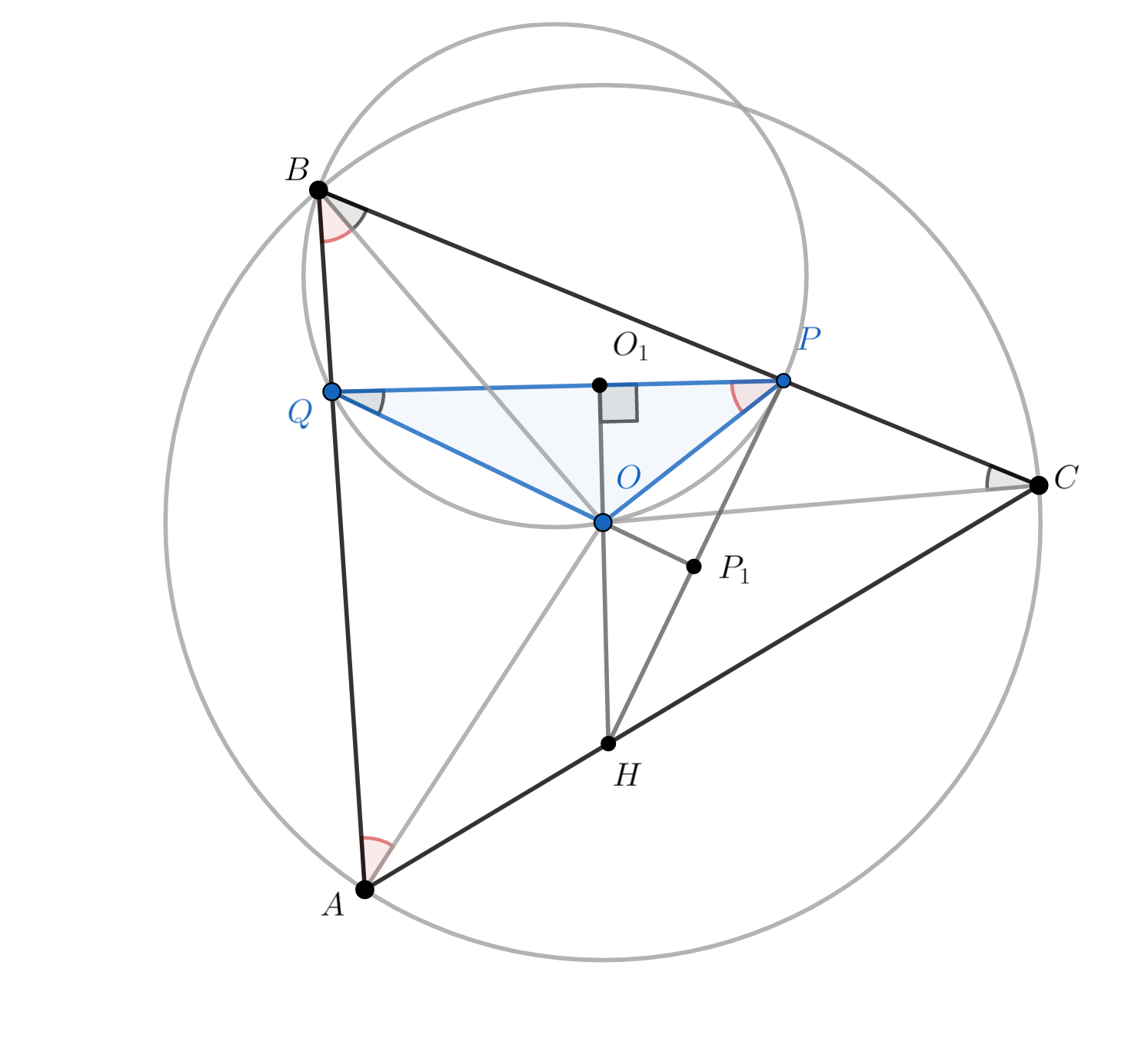
Угол — внешний угол треугольника
поэтому
Значит, четырёхугольник
вписан, и
Пусть
— точка пересечения прямых
и
Вновь по свойству внешних
углов
Итак, то есть
— ортоцентр треугольника
Ошибка.
Попробуйте повторить позже
Даны трое чашечных весов без гирь, из которых ровно одни сломаны: их показания произвольны, и мы не знаем, какие весы
неисправны. Докажите, что из монет можно определить одну фальшивую (более легкую) не более, чем за
взвешивание.
Источники:
Докажем индукцией по
База. Для удобства занумеруем монеты числами от до
и запишем их в троичной записи (таким образом, каждой монете
сопоставлена пара цифр от
до
). Первое взвешивание делаем первыми весами в соответствии с первой цифрой номера: на левую чашу
кладем монеты, у номера которых первая цифра
на правую — у которых она
Второе взвешивание делаем аналогично вторыми
весами в соответствии со второй цифрой номера. Знак
указывает на то, что фальшивая монета среди чисел с
на первом/втором
месте,
— что она среди чисел с
на первом/втором месте,
— что среди чисел с
на первом/втором месте. После проведения
взвешиваний можно перенумеровать числа так, чтобы результат первого взвешивания указывал на число с
на первом месте, а
второго — с
на втором. Тогда
монеты без нулей в номере точно не фальшивые (иначе соврали и первые, и вторые
весы).
Теперь разобьем монеты на три группы следующим образом: в одну поместим в другую
и
в третью —
и
дополним
все группы до трех монет точно не фальшивыми и взвесим третьими весами. Если весы сказали, что фальшивая в группе с
то это и есть
(иначе двое весов соврали), и четвертое взвешивание не понадобилось. Если взвешивание сказало, что фальшивая в группе с
и
то третьи весы противоречат вторым. Поэтому хотя бы одни из них соврали, а значит, первые точно исправны. Но тогда у фальшивой
первая цифра действительно
таким образом, остались лишь три кандидата на фальшивую монету и одни точно исправные весы,
которыми мы находим фальшивую монету за
ход. Аналогично поступаем, если третье взвешивание сказало, что фальшивая монета в
группе с
и
Переход. Разобьём монет на одну
куч по
в каждой. Будем считать каждую кучу за одну монету (куча с фальшивой
монетой легче). Тогда по рассуждениям из базы мы либо находим за
взвешивания кучу с фальшивой монетой и далее работаем с ней,
пользуясь предположением, либо за
взвешивания мы находим рабочие весы и три кучи, среди которых есть куча с фальшивой
монетой. Во втором случае, нам хватит
взвешиваний, если постоянно делить кучу на три кучи с одинаковым числом
монет.



