Тема 18. Задачи с параметром

18.07 Алгебра. "Гвозди" для квадратичной функции

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи с параметром

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80060

Найдите все значения $a,$ при которых неравенство

8x2-− 20x+-16 4x2− 10x+ 7 ≤ a

является верным при всех значениях $x.$

Показать ответ и решение

2 2 4x − 10x+ 7= (2x− 2,5) +0,75>0

Значит можно домножить обе части на знаменатель и знак не изменится.

2 2 8x − 20x+ 16 − 4ax +10ax− 7a≤ 0

(4a− 8)x2+ (20 − 10a)x +7a− 16≥ 0

Случай, когда это не квадратный трёхчлен

1.

$a =2$

−2≥ 0-не правда

2.

$a <2$ Тогда если рассмотреть функцию $f$ :

f(x)= (4a− 8)x2+ (20− 10a)x +7a− 16

Это парабола, верви которой направлены вниз, вершина параболы

20− 10a 10 5 x0 =− 2(4a−-8) = 8-= 4

$f(x)$ убывает на $(5;+∞ ) 4$ - значит, нам этот случай не подходит.

3.

$a >2$ Тогда

D = (10(2− a))2− 4(4a− 8)(7a− 16)≤ 0

(a− 2)(25a− 50− 28a+ 64)≤0

a≥ 14 3

Ответ:

$a ≥ 14 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#18411

При каких $a$ ровно один корень уравнения

2 x − ax +2 = 0

удовлетворяет условию $1< x< 3?$

Показать ответ и решение

Рассмотрим функцию $2 y = x − ax+ 2.$ Графиком является парабола с ветвями вверх.

Дискриминант $D = a2− 8$ может быть как отрицательным (что не подходит для нашей задачи), равным нулю или положительным (два этих случая нам как раз и нужно исследовать).

Рассмотрим отдельно случай, когда $D = 0$ , то есть $a= ±2√2-$ . При $a= 2√2-$ уравнение имеет единственный корень $x = √2$ , при $a= −2√2-$ корень равен $x= −√2.$ Второй случай не удовлетворяет условию $1 < x< 3.$ Следовательно, подходит только $√- a = 2 2$ .

Рассмотрим случай $D > 0.$ Удовлетворять условию $1 < x< 3$ может либо левый $x1$ , либо правый $x2$ корень уравнения. Если $1< x1 < 3$ , то $x2 ≥ 3$ . Если $1 < x2 < 3$ , то $x1 ≤1$ .

Проверим отдельно, чему равен один из корней уравнения, когда другой равен 1 или 3 для того, чтобы далее рассматривать только строгие неравенства.

Если $y(1)= 3− a= 0$ , то $a= 3$ , тогда второй корень равен 2, что нам подходит.

Если $y(3)= 11− 3a= 0$ , то $11 a= 3-$ , то другой корень равен $2 3$ , что нам не подходит.

Теперь если $1 < x1 < 3$ , то $x2 > 3$ .

Если $1 < x2 < 3$ , то $x1 <1$ (см рис). Заметим, что условия для обеих картинок можно записать одной системой, так как получаем то, что числа $y(1)$ и $y(3)$ должны быть разных знаков, то есть их произведение должно быть отрицательным.

$PIC$

{ 2 D = a − 8> 0 y(3)⋅y(1)< 0

{ D = a2− 8> 0 (11− 3a)(3− a)< 0

Решая систему, получаем $( ) a ∈ 3; 11 . 3$

Объединяя подходящие значения параметра, получаем окончательно

√ - [ 11) a ∈ {2 2}∪ 3;-3

Ответ:

$√ - [ 11) a ∈{2 2} ∪ 3; 3$

Ошибка.
Попробуйте повторить позже

Задача 3#36626

При каких значениях параметра $a$ уравнение

2 x +2(a− 2)x− 4a+ 5= 0

имеет два различных корня, причем оба больше $− 1?$

Показать ответ и решение

Рассмотрим функцию

2 y = x + 2(a − 2)x− 4a+ 5

Графиком является парабола с ветвями вверх:

$PIC$

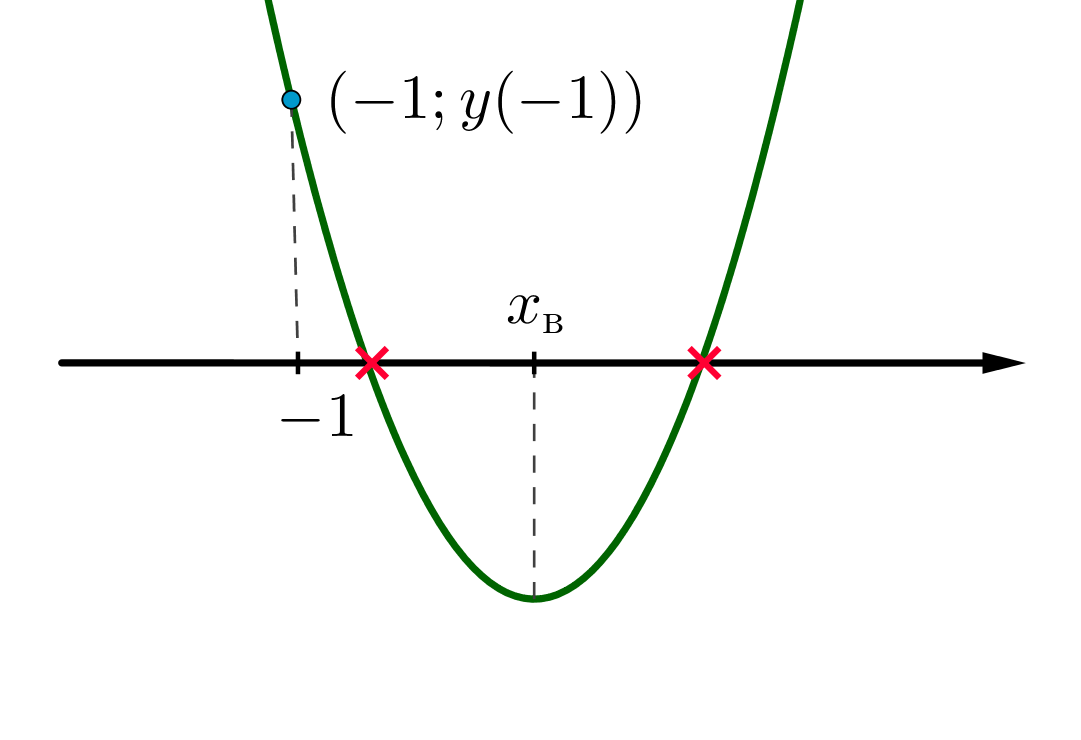
Чтобы оба корня были больше -1, нужно следующее:

$pict$

Всего существует пять мест, куда можно поставить число относительно корней уравнения: слева направо $I,$ $II,$ $III,$ $IV,$ $V.$ Нам подходит лишь место $I.$ В этом месте значение функции во всех точках положительное. Но так как в $V$ месте значение функции во всех точках тоже положительное, то дополнительно накладывается условие на абсциссу вершины параболы: что она больше -1.

Решая систему выше, получаем

( ) a ∈(−∞; −1)∪ 1; 5 3

Расшифровка:
$I$ — левее левого корня
$II$ — в левом корне
$III$ — между корнями
$IV$ — в правом корне
$V$ — правее правого корня

Ответ:

$( ) a ∈(−∞; −1)∪ 1; 5 3$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Ответ может отличаться от верного включением точки $a= 53$	3

Все неравенства для выполнения условия задания составлены верно, но в решении есть ошибка или оно не завершено	2

Верное введение функции и её исследование	1
ИЛИ
Верно найдены корни квадратного уравнения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 4#388

Найдите все значения параметра $a,$ при каждом из которых множество решений неравенства

3x2− (a + 1)x− a2− a+ 1 <0 4

содержит отрезок $[− 2;2].$

Показать ответ и решение

Рассмотрим функцию

f (x)= 3 x2− (a +1)x− a2− a+ 1 4

Тогда наше неравенство имеет вид $f(x)< 0.$

При каждом фиксированном $a$ графиком функции $y = f(x)$ является парабола, причем ветви параболы направлены вверх. Если неравенство $f(x) < 0$ имеет решения, то существуют точки, принадлежащие параболе, которые находятся ниже оси абсцисс. Следовательно, уравнение $f(x)= 0$ имеет два различных корня, то есть парабола пересекает ось абсцисс в двух точках $x1 <x2.$

Тогда интервал $(x1;x2)$ является решением неравенства $f(x)< 0.$ Отрезок $[−2;2]$ содержится в интервале $(x1;x2),$ если числа $x = −2$ и $x =2$ находятся между корнями $x1$ и $x2.$ Получаем картинку ниже:

$PIC$

Эта картинка задается следующими условиями:

({ ( √ --) f(−2)< 0 ⇒ a ∈ −∞;− 3+---17- ∪ (3;+∞ ) ( f(2)< 0 2

Замечание.

Если существует хотя бы одна точка $x= x0,$ в которой $f(x0)< 0,$ где графиком $y = f(x)$ является парабола с ветвями вверх, то автоматически эта парабола пересекает ось абсцисс в двух точках, то есть выполнено условие $D > 0$ для уравнения $f(x)= 0.$ Следовательно, в нашей системе требование существования двух различных корней уравнения $f(x)= 0$ является излишним.

Ответ:

$( 3+ √17-) a ∈ −∞; −---2--- ∪ (3;+ ∞)$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточно обоснованные переходы	3

Все неравенства для выполнения условия задания составлены верно, но в решении есть ошибка или оно не завершено	2

Верное введение функции и её исследование (обосновано, что график функции парабола при любом $a$ )	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 5#1081

При каких значениях параметра $a$ решением неравенства

2 ( 2 ) 2 x − a − 2a− 3 x+ a + 2≤ 0

является отрезок $[2;3]?$

Показать ответ и решение

Рассмотрим множество функций

2 2 2 fa(x)= x − (a − 2a− 3)x +a + 2

При каждом фиксированном $a$ это квадратичная функция, графиком которой является парабола с ветвями, направленными вверх. При этом она может выглядеть как (1) $(D = 0),$ (2) $(D > 0)$ или (3) $(D < 0):$

$PIC$

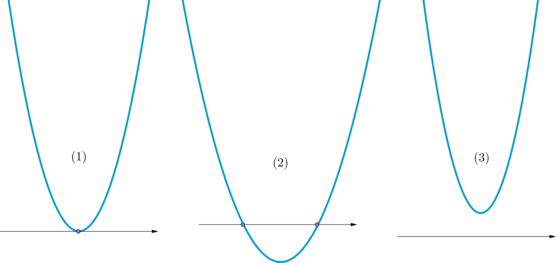
Для того, чтобы решением неравенства являлся отрезок $[2;3],$ необходимо, чтобы парабола выглядела как (2), то есть необходимо выполнение следующих условий:

(|{D = (a2− 2a− 3)2− 4(a2+ 2) >0 fa(2)= 0 |(f (3)= 0 ( a |{(a2− 2a− 3)2 − 4(a2+ 2)> 0 a2− 4a− 12= 0 |(a2− 3a− 10= 0 { (a2− 2a− 3)2− 4(a2+ 2) >0 a =− 2

Заметим, что при $a= −2$ неравенство $(a2− 2a− 3)2− 4(a2+ 2)> 0$ выполняется, так как оно равносильно $1> 0.$ Следовательно, получаем

a ∈{− 2}

Замечание.

Первое условие системы можно считать избыточным в том смысле, что дискриминант автоматически положителен при условии $fa(2)= fa(3)= 0,$ поскольку квадратный трехчлен имеет два корня $x= 2$ и $x = 3.$

Ответ:

$a ∈{− 2}$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточное обоснование (некоторые переходы не расписаны)	3

Верно наложены все условия для того, чтобы решением неравенства являлся заданный отрезок, но в решении есть ошибка или оно не завершено	2

Верное введение функции и её исследование	1
ИЛИ
верно найдены корни квадратного уравнения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 6#1123

При каких значениях параметра $a$ число 3 заключено между корнями уравнения

2 x − (2a − 1)x+ 4− a = 0 ?

Показать ответ и решение

Рассмотрим функцию

2 y = x − (2a − 1)x+ 4− a

Ее графиком является парабола, ветви которой направлены вверх и которая должна пересекать ось абсцисс в двух точках. Чтобы выполнялось условие задачи, нужно, чтобы парабола выглядела так:

$PIC$

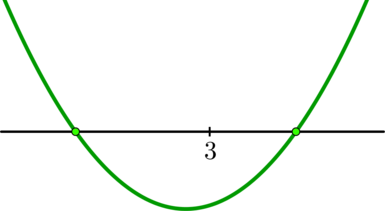
Значит, необходимо:

16 y(3)< 0 ⇒ a > 7

Ответ:

$( 16 ) a ∈ 7 ;+∞$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточно обоснованные переходы	3

Все неравенства для выполнения условия задания составлены верно, но в решении есть ошибка или оно не завершено	2

Верное введение функции и её исследование	1
ИЛИ
Верно найдены корни квадратного уравнения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#1294

Найдите все положительные значения параметра $a$ , при каждом из которых оба корня уравнения

2 2 (1 − a)x − 2ax + 1 = 0

не меньше $− 3$ .

Показать ответ и решение

По условию уравнение должно иметь два корня, значит, оно квадратное и имеем условия на старший коэффициент и дискриминант:

2 2 1− a ⁄= 0, D = 4(2a − 1) > 0

Графиком функции

f(x) = (1 − a2)x2 − 2ax + 1

при каждом фиксированном $a$ является парабола.

Рассмотрим два случая в зависимости от направления ветвей параболы.

(1) Ветви направлены вверх:

1 − a2 > 0 ⇒ − 1 < a < 1

$PIC$
(2) Ветви направлены вниз:

2 1− a < 0 ⇒ a < − 1 или a > 1

$PIC$

Таким образом, для положительных по условию значений $a$ имеем совокупность двух случаев:

( ⌊|| D > 0 ⌊ (|a ∈ (− ∞; − √1) ∪( 1√-;+∞ ) |||||{ || |||{ 2 2 || 0 < a < 1 || 0 < a[ < 1 √-- √ --] ||||| f(− 3) ≥ 0 || |||a ∈ 13(1− 11); 13(1+ 11) ||||( xверш = ---2a--- > − 3 || |(a ∈ (− ∞; − 1) ∪(1(1− √37-);1) ∪(1(1+ √37-);+ ∞ ) || 2(1− a2) ⇒ || ( ( ) 6( ) 6 ⇒ ||( || ||a ∈ − ∞; − √1 ∪ 1√-;+∞ |||||{ D > 0 || ||{ 2 2 || a > 1 || a > 1( √ --] [ √ -- ) ⌈||| f(− 3) ≤ 0 ⌈ ||||a ∈ − ∞; 13(1− ( 11) ∪√ 13(1+) 1(1);+ ∞√ -- ) ( xверш > − 3 (a ∈ (− ∞; − 1)∪ 16(1− 37);1 ∪ 16(1+ 37);+ ∞

( 1 ) [1+ √11- ) ⇒ a ∈ √--;1 ∪ -------;+∞ 2 3

Заметим, что условие $xверш > − 3$ важно. Без этого условия возможен еще один случай, который нам не подходит. Например:

$PIC$

Ответ:

$( ) [ √ -- ) a ∈ √1-;1 ∪ 1+---11-;+ ∞ 2 3$

Ошибка.
Попробуйте повторить позже

Задача 8#1331

Найдите все значения параметра $a,$ при каждом из которых неравенство

2 2 a x − 2a(a− 3)x − 18 ≤0

имеет решения, и все эти решения принадлежат отрезку $[−1;2].$

Показать ответ и решение

При $a =0$ неравенство принимает вид $− 18≤ 0,$ что верно при любом значении $x ∈ℝ.$

Так как $ℝ$ не содержится в отрезке $[−1;2],$ то значение параметра $a= 0$ не подходит.

Далее будем считать, что $a ⁄= 0.$

Тогда старший коэффициент $a2 >0,$ следовательно, при каждом фиксированном $a$ ветви параболы

2 2 f(x)= a x − 2a(a− 3)x− 18

направлены вверх.

Если дискриминант квадратного трехчлена $D < 0,$ то исходное неравенство не имеет решений. Следовательно, этот случай нам не подходит.

Если $D ≥ 0,$ то решением неравенства будет отрезок $[x1;x2],$ где $x1,x2$ — корни уравнения

a2x2− 2a(a− 3)x − 18 =0

Заметим, что при $D = 0$ решением неравенства будет вырожденный «отрезок» $[x0;x0],$ состоящий из одной точки $x0 =x1 = x2$ — абсциссы вершины параболы.

Изобразим эскиз параболы, удовлетворяющей условию задачи:

$PIC$

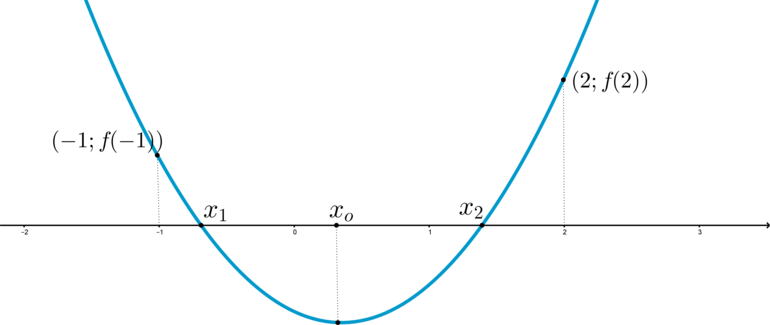
Здесь $2a(a−-3) a-− 3 x0 = 2a2 = a$ — абсцисса вершины параболы.

Для включения отрезка $[x1;x2]$ в отрезок $[−1;2]$ необходима система из условий:

(|f(−1)≥ 0 (|a ∈(−∞; 1− √7]∪ [1+ √7;+ ∞ ) ||{f(2)≥ 0 ||{a ≥ 3 √ - |−1 ≤ x ≤ 2 ⇒ |a ∈(2−∞; −3]∪ [3;+∞ ) ⇒ a∈ [1 + 7;+ ∞ ) ||( 02 2 ||( 2 D = 4a ((a− 3) +18)≥ 0 a ⁄=0

Ответ:

$a ∈[1+ √7;+ ∞)$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Ответ может отличаться от верного невключением граничного значения или не рассмотрен случай $a= 0$	3

Для $a2 ⁄=0$ рассмотрена квадратичная функция, верно наложены все условия того, чтобы решения неравенства принадлежали данному отрезку, но в ходе решения системы допущена ошибка	2

Рассмотрен верно случай $a2 = 0$	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 9#1709

Найдите все значения параметра $a$ , при каждом из которых один корень уравнения

ax2 + 4x + a + 1 = 0

больше 1, а другой меньше 1.

Показать ответ и решение

Рассмотрим два случая:

1) $a = 0$ . Тогда уравнение становится линейным и $1- x = − 4$ . Это значения параметра нам не подходит.

2) $a ⁄= 0$ . Тогда уравнение является квадратным. Его дискриминант $D = 4(4 − a2 − a)$ .

Если $( √ --- √ --) D > 0 ⇒ a ∈ −-1 −---17; −-1-+--17 ⇒ 2 2$ уравнение $ax2 + 4x + a + 1 = 0$ имеет два корня.

Графиком функции $f(x) = ax2 + 4x + a + 1$ при каждом фиксированном $a$ является парабола,

причем при $( √ --) −-1 +---17 a ∈ 0; 2$ ветви направлены вверх, при $( √ --- ) − 1-−--17- a ∈ 2 ;0$ ветви направлены вниз:

$PIC$

$PIC$

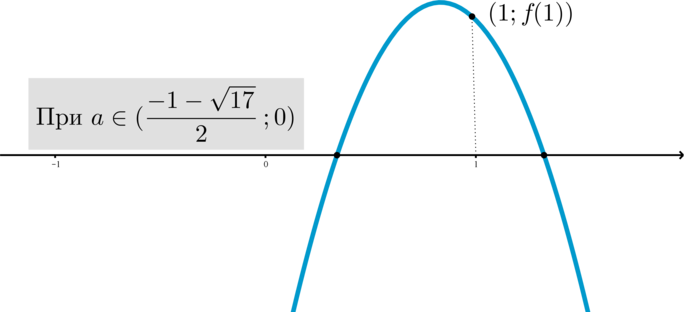
Для того, чтобы уравнение имело один корень больше $1$ , а другой меньше 1, нужно:

⌊ ( √ --- { − 1 + 17 | 0 < a < -----2---- || ( | f(1) < 0 5- || ( √ --- =⇒ − 2 < a < 0 |⌈ { −-1 −---17 < a < 0 ( 2 f(1) > 0

Ответ:

$( ) a ∈ − 5;0 2$

Ошибка.
Попробуйте повторить позже

Задача 10#1710

Найдите все положительные значения параметра $a$ , при каждом из которых оба корня уравнения

2 2 (1− a )x − 2ax +1 = 0

не меньше $− 3$ .

Показать ответ и решение

Так как уравнение должно иметь два корня, то оно должно быть квадратным, то есть $1− a2 ⁄= 0$ и дискриминант $D = 4(2a2 − 1)> 0$ .

Графиком функции $f(x) =(1− a2)x2− 2ax +1$ при каждом фиксированном $a$ является парабола.

(1) $1− a2 > 0 ⇒ −1 < a< 1$ и ветви параболы направлены вверх:

$PIC$

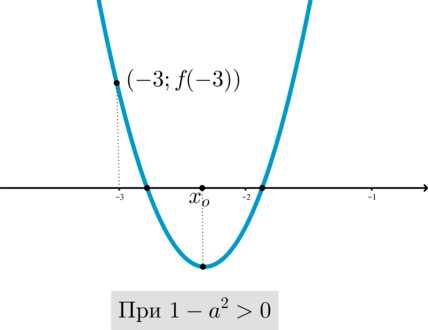
(2) $2 1− a < 0 ⇒ a< − 1 или a> 1$ ветви параболы направлены вниз:

$PIC$

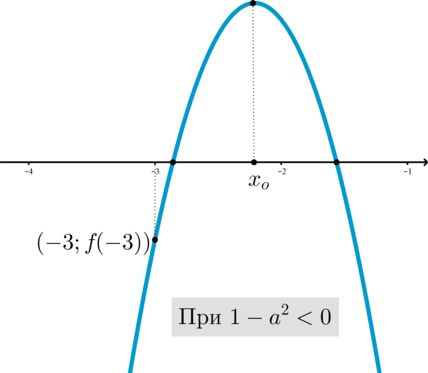
Таким образом, учитывая, что по условию нам нужны только положительные $a$ :

⌊(| ||||| D > 0 ||{ 0< a< 1 |||||| f(−3)≥ 0 ||||( xo =---2a-2-> −3 ( ) ( √ -- ) || 2(1− a ) =⇒ a∈ √1-;1 ∪ 1-+--11;+∞ ||(| D > 0 2 3 ||||{ a> 1 ||⌈| f(−3)≤ 0 ||( xo > −3

Заметим, что условие $xo > −3$ важно. Без этого условия возможен еще один случай, который не удовлетворяет нашему условию. Например:

$PIC$

Ответ:

$( 1 ) ( 1+ √11 ) a ∈ √2;1 ∪ ---3--;+ ∞$

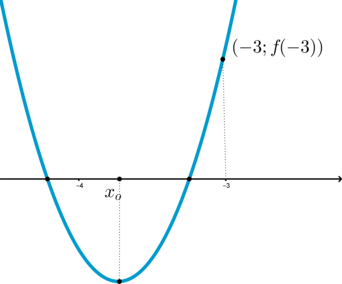
Ошибка.
Попробуйте повторить позже

Задача 11#2543

При каких значениях параметра $a$ уравнение

2 2 x +3ax − a + 1 =0

имеет два корня из отрезка $[− 3;0]$ ?

Показать ответ и решение

Так как уравнение квадратное, то для того, чтобы оно имело два корня, необходимо, чтобы его дискриминант был больше нуля: $D = 13a2− 4> 0$ .

Для того, чтобы оба корня были из отрезка $[−3;0]$ , нужно, чтобы парабола $y = x2+ 3ax− a2+ 1$ выглядела так:

$PIC$

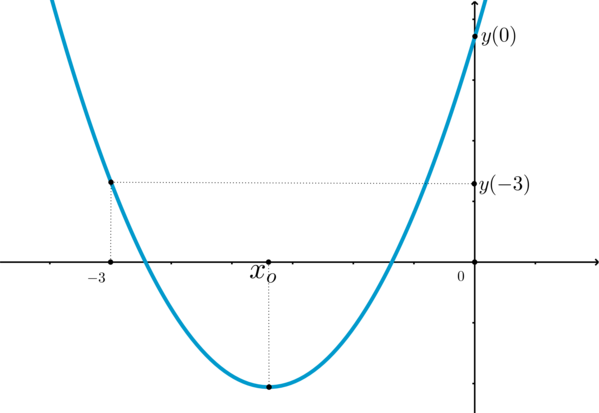
Заметим, что $3a x0 =− 2-$ — вершина параболы.

То есть нужно выполнение сразу нескольких условий:

( (||a ∈( −∞;− √2-)∪ (√2-;+∞ ) |||{D > 0 |||{ 13 13 y(−3) ≥0 ⇒ − 10≤ a≤ 1 |||(y(0)≥ 0 ||||− 1≤ a≤ 1 − 3< x0 < 0 |(0 < a< 2

Решив последнюю систему, получим $( ] a ∈ √213;1$ .

Ответ:

$( -2-- ] a ∈ √13;1$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#2655

При каких значениях параметра $a$ неравенство

(√ ------- ) (√ ------- ) loga 1 − x2 + 1 + loga 1 − x2 + 7 < 1

справедливо для каждого допустимого значения $x$ ?

Показать ответ и решение

ОДЗ неравенства: $|x| ≤ 1$ .
Заметим, что при всех $x$ из ОДЗ аргументы обоих логарифмов положительны.
Пусть $------- t = √ 1 − x2 + 1$ . Так как $|x | ≤ 1$ , то $------- √ 1 − x2 ∈ [0;1]$ , следовательно, $t ∈ [1; 2]$ . Тогда исходное неравенство относительно $x$ будет иметь решения при всех $x$ из ОДЗ, если полученное неравенство

logat + loga (t + 6) < 1

относительно $t$ будет иметь решения при всех $t ∈ [1;2]$ . Полученное неравенство можно переписать в виде

logat(t + 6) < 1

1) Пусть $a > 1$ . Тогда неравенство равносильно

t2 + 6t − a < 0

Графиком функции $2 y = t + 6t − a$ является парабола, ветви которой направлены вверх, следовательно, решением неравенства $y < 0$ может быть либо интервал (если $D > 0$ ), либо пустое множество (если $D ≤ 0$ ). Следовательно, нужно, чтобы решением неравенства $y < 0$ был интервал, который содержал в себе отрезок $[1;2]$ . Нам подходит такая картинка:
$PIC$
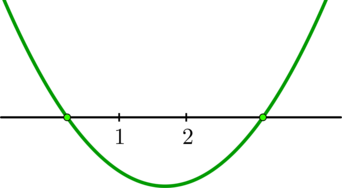
То есть числа $1$ и $2$ должны находиться строго между корнями уравнения $y = 0$ . Это задается следующими условиями:

( ( |{ y(1) < 0 |{ 7 − a < 0 y(2) < 0 ⇒ 16 − a < 0 ⇒ a > 16 |( |( D > 0 36 + 4a > 0

Найденные $a$ подходят под условие $a > 1$ .

2) Пусть $0 < a < 1$ . Тогда неравенство равносильно

t2 + 6t − a > 0

В этом случае решением неравенства $y > 0$ может быть либо объединение двух лучей ( $D ≥ 0$ ), либо все $ℝ$ ( $D < 0$ ). Заметим, что абсцисса вершины параболы $t0 = − 3$ . Следовательно, для того, чтобы неравенство выполнялось при всех $t ∈ [1;2]$ , нам подходят следующие положения параболы $y = t2 + 6t − a$ : $PIC$
Первые два положения задаются условием $D ≤ 0$ , в этом случае отрезок $[1;2]$ содержится в решении неравенства $y > 0$ .
Третье положение задается условием $D > 0$ , и чтобы отрезок $[1;2]$ содержался в решении, нужно, чтобы число $1$ находилось правее правого корня, следовательно, $y(1) > 0$ (левее левого корня $1$ располагаться не может, так как абсцисса вершины параболы равна $− 3$ ). Следовательно:

⌊ D ≤ 0 | { ⌈ D > 0 ⇒ a < 7 y(1) > 0

Так как этот случай был возможен при $a ∈ (0;1)$ , то, пересекая эти значения с $a ∈ (− ∞; 7)$ , получим $a ∈ (0;1)$ .

Объединяя найденные $a$ в обоих пунктах, получим окончательный ответ

a ∈ (0;1) ∪ (16;+ ∞ )

Ответ:

$a ∈ (0;1) ∪ (16;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 13#2674

Найдите все значения параметра $a$ , при каждом из которых решение неравенства

2 2 (a + 2a− 3)x − (3a+ 1)x+ 2 ≥ 0

содержит отрезок $[1;4]$ .

Показать ответ и решение

Перепишем неравенство в виде

2 (a− 1)(a+ 3)x − (3a +1)x+ 2≥ 0

Рассмотрим следующие случаи.

1) $(a− 1)(a+ 3)= 0$

В этом случае неравенство становится линейным:

⌊ ({a = 1 | || (x ≤ 1 ||| ({a = 2−3 ⌈ 1 (x ≥ −4

Видим, что только при $a = −3$ решение неравенства содержит отрезок $[1;4].$

Следовательно, $a= − 3$ пойдет в ответ.

(a− 1)(a +3)> 0 a∈ (−∞;− 3)∪(1;+∞ )

В этом случае неравенство является квадратичным, причем при каждом фиксированном $a$ графиком

2 f(x)= (a − 1)(a+ 3)x − (3a+ 1)x + 2

является парабола, ветви которой направлены вверх.

Рассмотрим уравнение

2 (a− 1)(a+ 3)x − (3a +1)x+ 2= 0

Найдем дискриминант

2 2 D = a − 10a +25 =(a− 5)

2.1) При $a = 5$ получаем $D = 0$ и парабола $f(x)$ имеет ровно одну точку пересечения с осью $Ox :$

$PIC$

Тогда решением неравенства являются все $x ∈ ℝ,$ что в свою очередь содержит отрезок $[1;4].$ Следовательно, $a =5$ пойдет в ответ.

2.2) При $a ∈(−∞; −3)∪ (1;5)∪ (5;+∞ )$ получаем $D > 0$ и парабола $f(x)$ имеет две точки пересечения с осью $Ox :$

x = 3a+-1−-|a-− 5|, x = 3a+-1+-|a-− 5| 1 2(a − 1)(a+ 3) 2 2(a− 1)(a+ 3)

и решением неравенства являются

x∈ (−∞;x1]∪ [x2;+∞ )

Для того, чтобы решение содержало отрезок $[1;4],$ необходимо, чтобы парабола задавалась одним из двух видов:

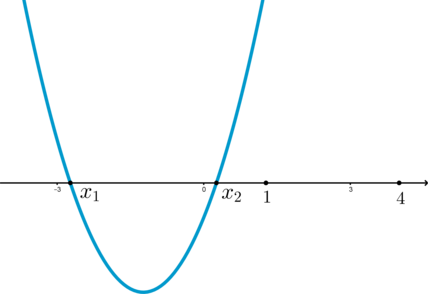$PIC$ или $PIC$

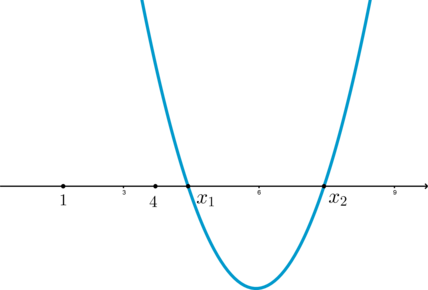
Тогда имеем систему и далее совокупность двух случаев:

⌊ ( | |||||a ∈ (− ∞;−3)∪ (1;5) || |{⌊ x1 = 3a+-1+-a-− 5-≥ 4 || ||| 2(a− 1)(a+ 3) ( || |||||⌈ 3a+-1−-a-+5- |{ a[∈ (− ∞;− 3) ∪(1;5)∪ (5;+ ∞) ||| ( x2 = 2(a− 1)(a+ 3) ≤ 1 | x1 ≥ 4 ⇔ || ( ( x2 ≤ 1 || ||||a ∈ (5;+∞ ) || ||{⌊ x1 = 3a+-1−-a-+5-≥ 4 ||| ||| 2(a− 1)(a+ 3) ⌈ |||||⌈ 3a+-1+-a-− 5 ( x2 = 2(a− 1)(a+ 3) ≤ 1

При $a< 5$ модуль $|a− 5|$ раскрывается отрицательно:

|a− 5|=− (a− 5)

При $a> 5$ модуль $|a− 5|$ раскрывается положительно:

|a− 5|= a− 5

Решением данной совокупности будут

a∈ (−∞; −3)∪ [2;5)∪(5;+∞ )

(a− 1)(a +3)< 0 a∈ (−3;1)

Тогда неравенство также является квадратичным и $f(x)$ — парабола, ветви которой направлены вниз.

При этих значениях $a$ также дискриминант $D > 0,$ но решением неравенства уже будут $x ∈[x1;x2].$

Для того, чтобы решение содержало отрезок $[1;4],$ необходимо, чтобы парабола выглядела следующим образом:

$PIC$

Тогда получаем систему

( |{a ∈(−3;1) ( 5] |f(1)≥ 0 ⇒ a∈ −3;− 2 (f(4)≥ 0

Объединяя все полученные значения для $a,$ получим окончательный ответ.

Ответ:

$( 5] a ∈ −∞; −2 ∪[2;+ ∞)$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Ответ отличается от верного невключением одной из точек	3

Рассмотрены случаи линейного неравенства и $D= 0$ верно, а случай $D >0$ не рассмотрен или рассмотрен с ошибкой	2
ИЛИ
рассмотрен верно только случай $D > 0$

Верно рассмотрен случай линейного неравенства	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 14#16774

Найдите все значения параметра $a,$ при которых уравнение

√ ----- x+ a= x

имеет ровно два решения.

Показать ответ и решение

Исходное уравнение равносильно системе

( { x2− x− a =0 ( x ≥0

Cпособ 1.

Система имеет два решения тогда и только тогда, когда уравнение $x2− x − a = 0$ имеет два неотрицательных решения. Следовательно, если рассмотреть функцию $2 y = x − x− a,$ то должно быть выполнено:

(| (| ||{ D > 0 ||{1 +4a > 0 y(0) ≥0 ⇔ − a≥ 0 ⇔ − 1 < a≤ 0 |||( |||( 1 4 x(верш) > 0 2 > 0

Cпособ 2.

Перепишем систему в виде

({ 2 a= x − x ( x≥ 0

Будем рассматривать параметр $a$ как переменную. Построим в системе координат $xOa$ множество $S$ решений системы. Если некоторая точка плоскости с координатами $(x0;a0)$ принадлежит этому множеству $S,$ то для исходной задачи это означает, что если параметр $a$ принимает значение $a0,$ то $x0$ будет одним из решений системы. Нас просят найти все такие значения $a0$ параметра $a,$ при каждом из которых ровно де точки вида $(x0;a0),$ где $x0 ≥ 0,$ принадлежат множеству решений $S,$ изображенному на плоскости $xOa.$ Фактически это равносильно тому, что горизонтальная прямая $a= a0$ имеет две точки пересечения с множеством $S.$

График $a= x2− x$ — парабола, пересекающая ось абсцисс в точках $x = 0$ и $x = 1,$ а также пересекающая прямую $x= 0$ в точке $(0;0).$ Следовательно, множество $S$ выглядит следующим образом:

$xy1201− 14$

Следовательно, горизонтальная прямая должна находиться между прямыми $1 a = −4$ не включительно и $a= 0$ включительно. Тогда подходят значения параметра

1 −4 < a≤ 0

Ответ:

$( 1 ] a ∈ −4;0$

Ошибка.
Попробуйте повторить позже

Задача 15#17311

При каких значениях параметра $a$ уравнение

22 2 2 ax +(2a − 3)x +a +1 = 0

имеет решения и все решения принадлежат промежутку $(0;1)?$

Показать ответ и решение

Сначала рассмотрим отдельно случай $a= 0.$ При этом квадратное уравнение обращается в линейное:

1 − 3x + 1= ⇔ x = 3 ∈ (0;1)

Получили, что $a = 0$ нам подходит.

Далее считаем, что $a ⁄=0.$ Тогда имеем дело с параболой

f(x)= a2x2+ (2a2− 3)x+ a2+ 1

Ветви параболы направлены вверх при любых $a,$ так как $a2 ≥ 0.$ Дискриминант должен быть неотрицательным, чтобы уравнение имело решения. Рассмотрим вершину параболы

x = − 2a2−-3= −1 + -3- верш 2a2 2a2

Для того чтобы точки пересечения параболы с осью $x,$ то есть решения уравнения, принадлежали промежутку $(0;1),$ вершина должна принадлежать этому промежутку, а значения в концах промежутка должны быть строго положительны. Соответствующее расположение изображено ниже.

$PIC$

Решим систему с перечисленными условиями:

$pict$

Поскольку $√ - 3 --3 4 < 2 ,$ то является пустым пересечение множеств

[ 3 3] − 4;4 ( ∘ -- √- ) (√ - ∘ -) − 3 ;− -3- ∪ --3; 3 2 2 2 2

Тогда решение всей системы — пустое множество и единственное подходящее значение параметра

a = 0

Ответ:

$a ∈{0}$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточное обоснование (некоторые переходы не расписаны) или не рассмотрен случай $a= 0$	3

Верно наложены все условия для того, чтобы выполнялось условие задания	2

Рассмотрен случай $a= 0$ и/или верное введение функции и её исследование	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 16#36623

При каких $a$ корни уравнения $x2+ x+ a= 0$ больше $a$ ?

Показать ответ и решение

Рассмотрим функцию $y = x2+ x+ a$ . Графиком является парабола с ветвями вверх. Чтобы оба корня были больше $a$ , нужно, чтобы

(| ||{ D =1 − 4a≥ 0 || y(a)> 0 |( xв > a

$PIC$

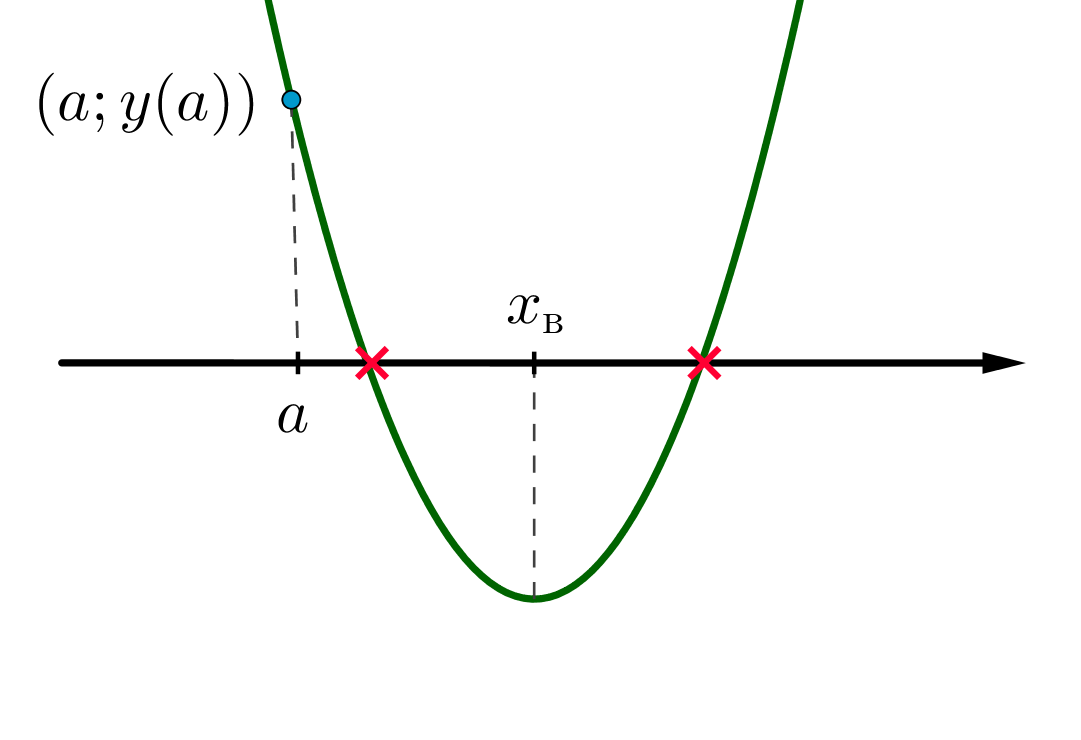
Всего существует пять мест, куда можно поставить число $a$ относительно корней уравнения: слева направо $I$ , $II$ , $III$ , $IV$ , $V$ . Нам подходит лишь $I$ . В этом месте значение функции во всех точках положительное. Но так как в $V$ месте значение функции во всех точках тоже положительное, дополнительно накладывается условие на абсциссу вершины параболы: что она больше $a$ .

Решая систему выше, получаем $a∈ (−∞; −2)$ .

Расшифровка:
$I$ – до левого корня,
$II$ – в левом корне,
$III$ – между корнями,
$IV$ – в правом корне,
$V$ – правее правого корня.

Ответ:

$a ∈(−∞;− 2)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#36624

Докажите, что уравнение

2 2 2 2 (a − a+ 1)x + (2a + 10a +3)x− 4a − 9a− 5= 0

имеет два различных корня при любом значении $a$ .

Показать ответ и решение

Нужно доказать, что $D> 0$ при любом $a$ . Заметим, что если мы будем выписывать дискриминант этого трехчлена, то получим

2 2 2 2 D = (2a + 10a+ 3) − 4(a − a+ 1)(−4a − 9a− 5)

– многочлен четвертой степени, который вряд ли удастся разложить на множители.

Будем рассуждать по-другому: если существует хотя бы одна точка $x 0$ , значение функции в которой всегда отрицательное (то есть при любом $a$ ) для параболы с ветвями вверх (какая у нас и есть), то это как раз и будет значить, что парабола пересекает ось $x$ в двух точках, то есть уравнение имеет два различных корня.

Эта точка легко подбирается – это $x0 = 1$ :

2 2 2 2 y(1)= a − a+1 +2a + 10a +3− 4a − 9a− 5= −a − 1< 0 ∀a

Следовательно, уравнение имеет два корня, причем можно заметить, что они расположены по разные стороны от числа $1$ .

Ответ:

Доказательство

Ошибка.
Попробуйте повторить позже

Задача 18#36625

При каких значениях параметра $a$ один корень уравнения

2 x +ax +4 = 0

меньше 2, а другой больше 2?

Показать ответ и решение

Рассмотрим функцию

2 y = x + ax+ 4

Ее графиком является парабола с ветвями вверх. Чтобы оба корня находились по разные стороны от числа 2, необходимо следующее:

( 2 { D = a − 16> 0 ( y(2) <0

Заметим, что условие на дискриминант в данном случае необязательно, так как если есть хотя бы одна точка, где значение функции отрицательно для параболы с ветвями вверх, то мы автоматически имеем два корня.

$PIC$

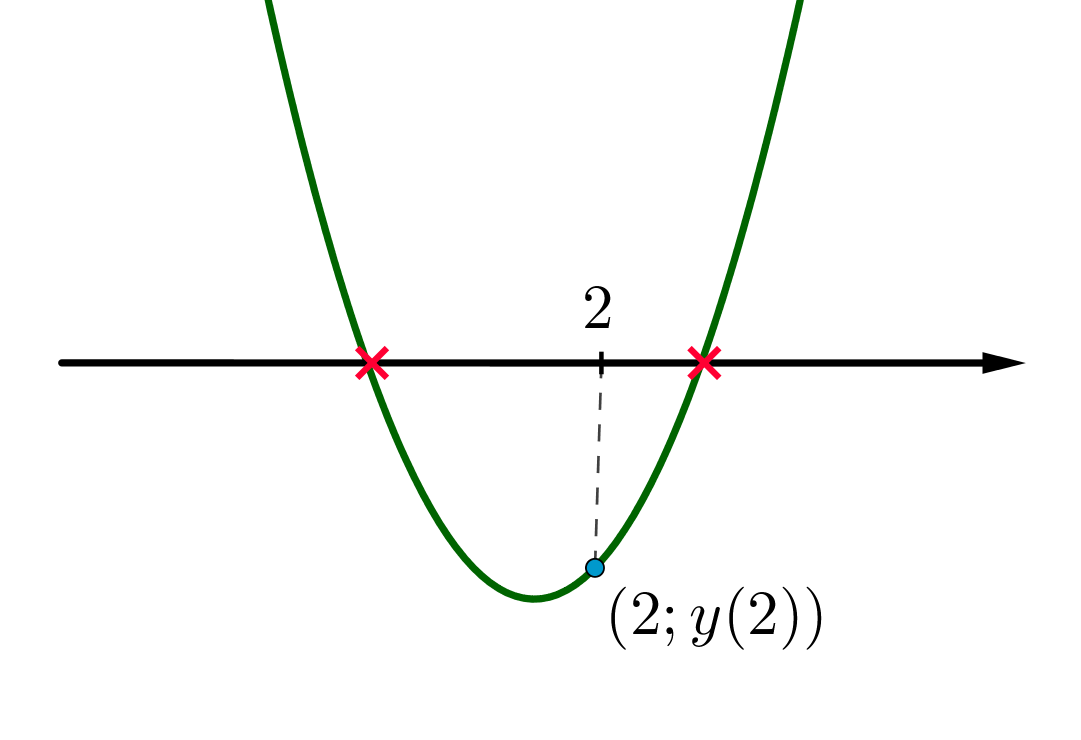
Всего существует пять мест, куда можно поставить число 2 относительно корней уравнения: слева направо $I, II, III, IV, V.$ Нам подходит лишь $III.$ В этом месте значение функции во всех точках отрицательное. И это единственное место, где значение функции отрицательное.

Решая систему выше, получаем

a ∈(−∞; −4)

Ответ:

$a ∈(−∞; −4)$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточно обоснованные переходы	3

Все неравенства для выполнения условия задания составлены верно, но в решении есть ошибка или оно не завершено	2

Верное введение функции и её исследование	1
ИЛИ
Верно найдены корни квадратного уравнения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 19#36627

При каких $a$ все корни уравнения

2 ax + (4− 2a)x + 1= 0

по модулю меньше 1?

Показать ответ и решение

Рассмотрим функцию

2 y = ax +(4− 2a)x+ 1

Ее графиком является парабола с ветвями вверх при $a> 0,$ либо парабола с ветвями вниз при $a < 0,$ либо прямая при $a = 0.$

Рассмотрим отдельно случай $a =0.$ Тогда имеем $y = 4x + 1.$ Точка пересечения с осью абсцисс — это $x = − 14.$ Она по модулю меньше 1. Следовательно, это значение параметра $a$ нам подходит.

Рассмотрим случай $a ⁄= 0.$ Число -1 должно находиться в $I$ месте, число 1 — в $V$ месте. Таким образом, чтобы оба корня по модулю были меньше 1, необходимо выполнение одной из двух систем (при $a > 0$ и $a< 0$ соответственно):

(| 2 (| 2 ||||D = (4− 2a) − 4a ≥ 0 ||||D = (4− 2a) − 4a≥ 0 |||||y(−1) >0 |||||y(−1)< 0 { { ||y(1)> 0 ||y(1)< 0 |||||xв = a−-2 ∈(−1;1) |||||xв = a-−-2∈ (−1;1) |||( a |||( a a > 0 a <0

$PIC$

Всего существует пять мест, куда можно поставить число относительно корней уравнения: слева направо $I,$ $II,$ $III,$ $IV,$ $V.$ Нам подходят лишь $I$ и $V.$ В этих местах значение функции во всех точках положительное, если ветви направлены вверх, и отрицательное, если ветви направлены вниз. Для того, чтобы оба числа 1 и -1 не попали оба, например, в $I$ место, дополнительно накладывается условие на абсциссу вершины параболы: что она по модулю меньше 1.

Объединяя решения систем выше между собой и с решением случая $a = 0,$ получаем

a∈ {0}∪[4;5)

Ответ:

$a ∈{0}∪ [4;5)$

Ошибка.
Попробуйте повторить позже

Задача 20#36628

При каких $a$ существует единственный корень уравнения

2 x − ax +2 =0

удовлетворяющий условию $1 <x <3$ ?

Показать ответ и решение

Рассмотрим функцию $y = x2− ax+ 2$ . Графиком является парабола с ветвями вверх.

Дискриминант $2 D = a − 8$ может быть как отрицательным, так и равным нулю.

Рассмотрим отдельно случай, когда $D =0$ , то есть $√- a= ±2 2$ . При $√- a= 2 2$ уравнение имеет единственный корень $√- x= 2$ , при $√- a =− 2$ корень равен $√- x= − 2$ . Второй случай не удовлетворяет условию $1< x< 3$ . Следовательно, подходит только $√- a =2 2$ .

Рассмотрим случай $D> 0$ . Удовлетворять условию $1 <x <3$ может либо левый $x1$ , либо правый $x2$ корень уравнения. Если $1 <x1 < 3$ , то $x2 ≥ 3$ . Если $1< x2 < 3$ , то $x1 ≤ 1$ . Тогда

$PIC$

({ D =a2− 8> 0 ( y(3)⋅y(1)< 0

Заметим, что условие на дискриминант в данной случае необязательно, так как если есть хотя бы одна точка, где значение функции отрицательно для параболы с ветвями вверх, то мы автоматически имеем два корня.

Всего существует пять мест, куда можно поставить число относительно корней уравнения: слева направо $I$ , $II$ , $III$ , $IV$ , $V$ . Нам подходят лишь $I$ или $V$ . В этих местах значение функции во всех точках положительное, если ветви направлены вверх. А также $III$ место, где значение функции отрицательное, если ветви направлены вверх.

Заметим, что если число 3 находится в $III$ , то число 1 не может попасть в $V$ , так как в таком случае было бы $3< 1$ , что неверно. Аналогично для второй картинки. Именно поэтому систему можно написать так сокращенно.