03 Динамика - Каталог заданий по ЕГЭ

Ошибка.
Попробуйте повторить позже

Задача 41#19908Максимум баллов за задание: 4

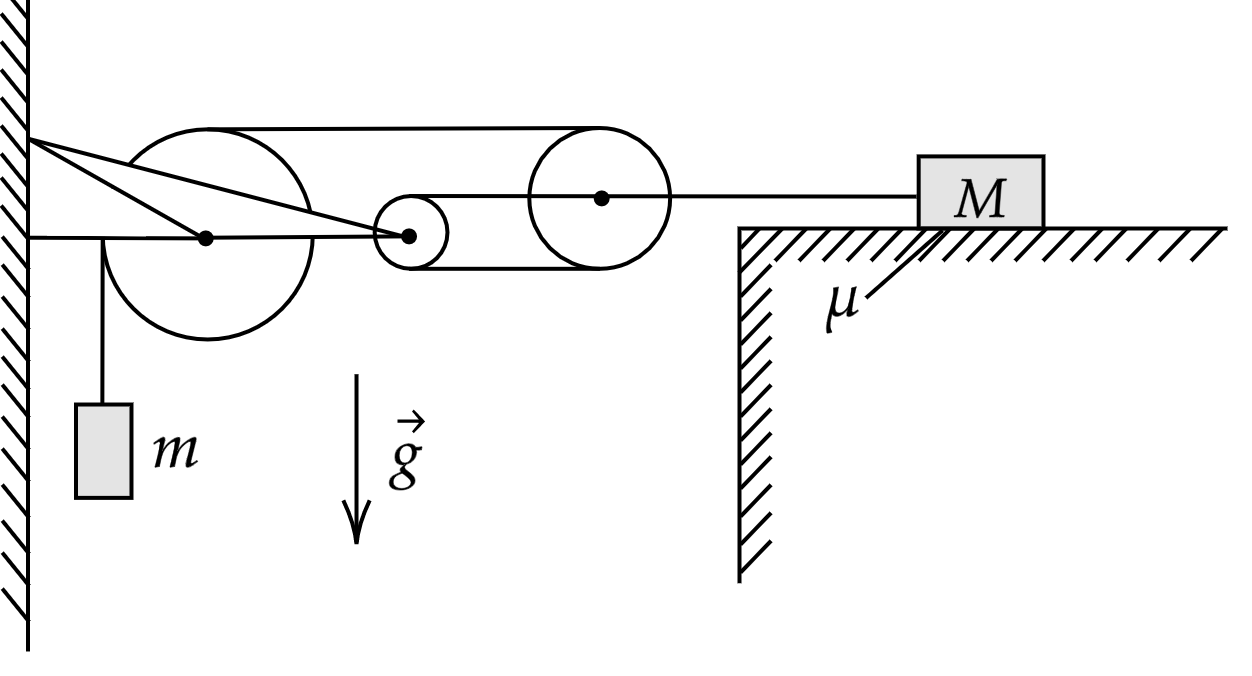
В системе, изображённой на рисунке, грузик массой $m = 1$ кг подвешен на нити, охватывающей три блока, второй конец которой привязан к оси самого правого блока (см. рис.). К этой же оси привязана другая нить, соединяющаяся с грузом массой $M = 11$ кг, лежащим на шероховатой горизонтальной плоскости (коэффициент трения груза о плоскость равен $μ = 0,25$ ). Найдите ускорение $a1$ грузика $m$ . Считайте, что нити невесомы и нерастяжимы, свободные участки нитей вертикальны или горизонтальны, блоки невесомы, а трение в их осях отсутствует. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

Сделаем рисунок с обозначением всех сил и введем оси координат $x$ и $y$ .

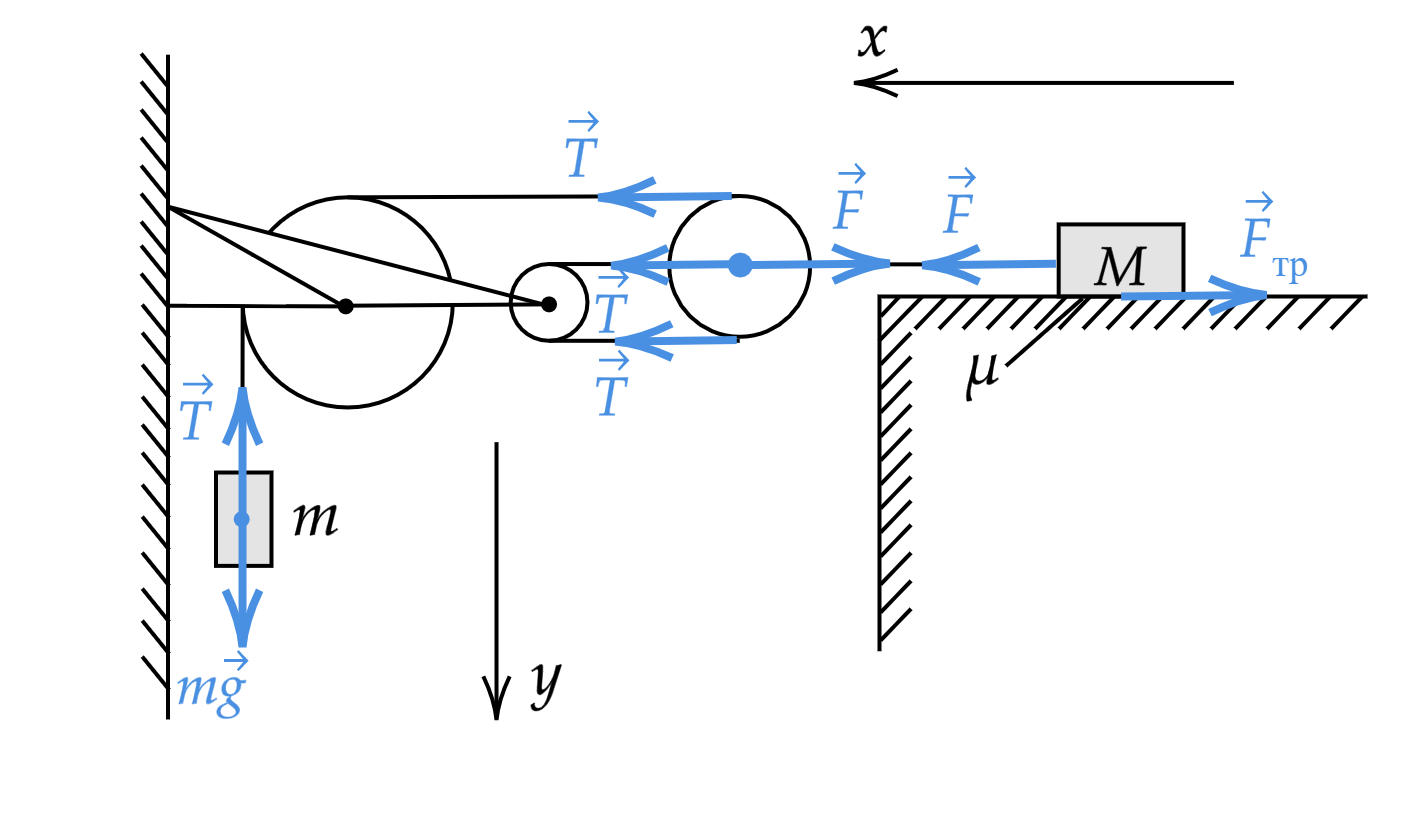
Воспользуемся вторым заоном Ньютона

( {mg − T = ma1 (F − F =Ma тр 2

Исходя из условий задачи сила натяжения первой нити по всей длине равна $T$ , а сила натяжения второй нити равна $F = 3T (1)$ . Кроме того при изменении положения грузика массой $m$ на $3x$ , груз массой $M$ сдвинется на $x$ , а это значит, что $a1 = 3a2 (2)$ . При $a1 > 0$ сила трения будет равна

F тр = μMg (3)

Подставим (1) , (2) и (3) в исходную систему уравнений

( { 3T = 3mg − 9ma2 ( 3T − μMg = Ma2

Вычтем из первого второе и получим

9ma2 − 3mg − μMg = Ma2

Отсюда

3m − μM a2 =g 9m-+-M--

А $a1$ с учетом (2) равно

a1 = 3a2 = 3g3m-−-μM-= 3 ⋅10 Н/кг3⋅1-кг−-0,25⋅11-кг= 0,375 м/с2 9m +M 9 ⋅1 кг+ 11 кг

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго закона Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатные оси, получено уравнение кинематической связи).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 42#19909Максимум баллов за задание: 4

В изображенной на рисунке системе на шероховатой поверхности находится тело массой $m = 1$ кг. При подвешивании к оси подвижного блока груза массой $M = 3$ кг он ( груз M) движется вниз с ускорением $a= 2$ м/с². Чему равен коэффициент $μ$ ? Нити нерастяжимы и невесомы, трением в осях пренебречь, блоки невесомы. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

$PIC$

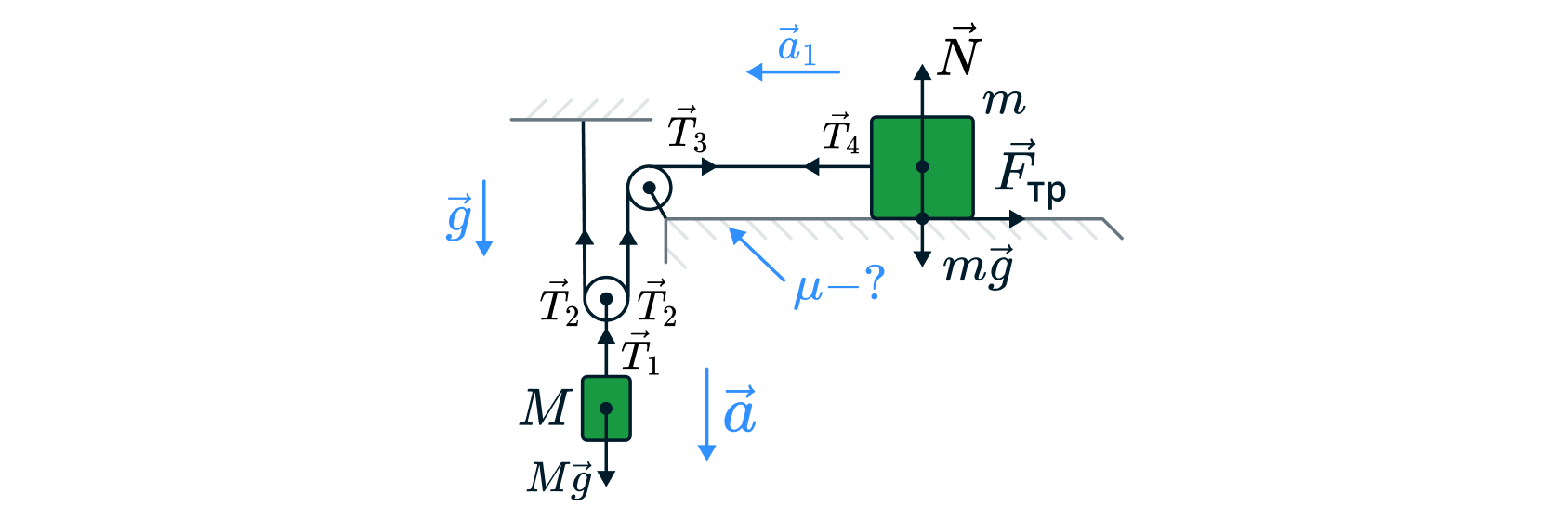
Т.к. блок невесомый, то записав в проекции на вертикальную ось второй закон Ньютона для него получим, что

T1 =2T2.

Также т.к. нить невесома и нерастяжима, то $T = T = T =T 2 3 4$ .
Запишем второй закон Ньютона на ось, направленную вертикально вниз, для груза массой $M$ .

Mg − 2T = Ma

где $T$ – сила натяжения нити. Отсюда сила натяжения нити

T = M-(g−-a) 2

Также напишем второй закон Ньютона на ось ,направленную горизонтально, для тела массой $m$ .

T − F тр = ma1

По рисунку видим, что изменение длины нити около тела массой $m$ в два раза больше, чем изменение длины нити у груза массой $M$ . Значит, что $a1 = 2a (2)$ Сила трения находится по формуле:

Fтр =μN =μmg (3)

Объединяя (1), (2) и (3) и выражая коэффициент трения, получим

M-(g−-a)− 2ma μ = ---2---------- mg

2 2 3-кг(10-м/с-− 2-м/с) − 2 ⋅1 кг⋅2 м/с2 μ = ---------2-1 кг⋅10-Н/кг----------= 0,8

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго закона Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатные оси, сказано как соотносятся ускорения тела и длина нити, получено уравнение кинематической связи).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 43#19910Максимум баллов за задание: 4

Зимой яхты вытаскивают из воды при помощи системы, изображенной на рисунке

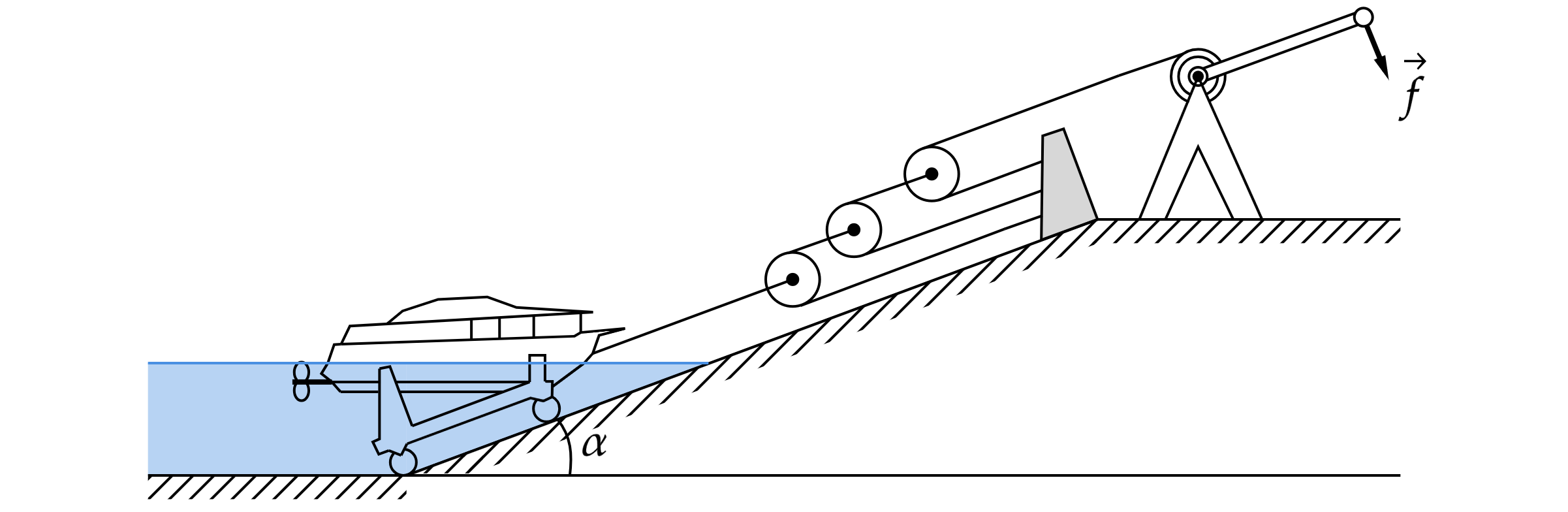
Найдите максимальную силу $f$ которую необходимо прикладывать к ручке лебёдки, чтобы медленно вытащить из воды судно водоизмещением 10 т при помощи, показанной на рисунке системы простых механизмов, если лебёдка дает выигрыш в силе в $n =5$ раз, а угол наклона слипа к горизонту равен $α = 0,1$ рад. Трением можно пренебречь. Примечания: водоизмещением называется масса воды, вытесняемой судном (измеряется обычно в тоннах); при углах $α< 0,1$ рад можно считать $sinα ≈α$ .

Показать ответ и решение

Данная система дает выигрыш в 5 раз, а система блоков в 8 раз. Максимальная сила будет приложена тогда, когда судно вытащили из воды, при этом будет действовать сила $8nf$ , яхта будет двигаться равномерно. Запишем второй закон Ньютона в проекции на наклонную плоскость

8nf = mgsinα⇒ f = mg-α = 10000-кг⋅10 Н/кг⋅0,1 рад-= 250 Н 8n 8⋅5

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 44#19940Максимум баллов за задание: 4

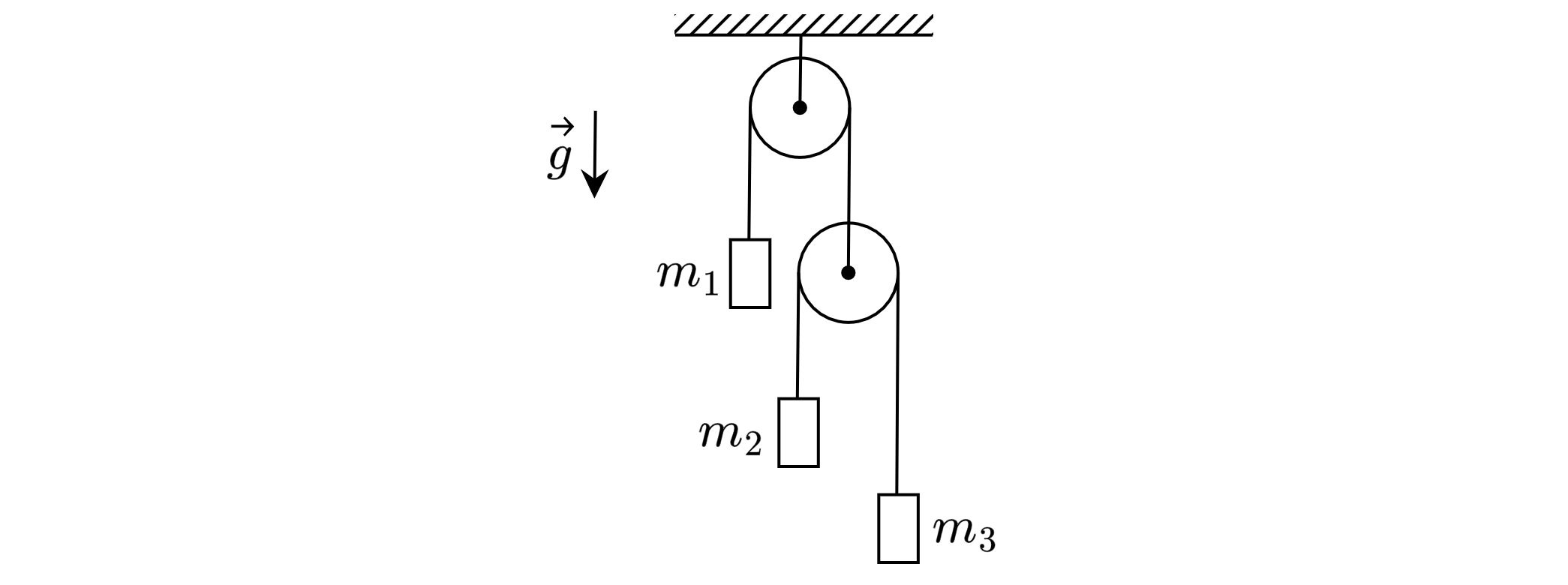
На рисунке изображена механическая система, состоящая из двух идеальных блоков, двух невесомых и нерастяжимых нитей и трёх грузов массами $m1 = 3$ кг, $m2 =m3 = 2$ кг, подвешенных на концах нитей. Определите, чему равна сила натяжения $T1$ нити, к которой подвешен груз $m1$ . Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй и третий законы Ньютона, записывать их будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

Пусть сила натяжения верхней нити $T1$ , а нижней $T2$ . Направим ось $x$ , как показано на рисунке.

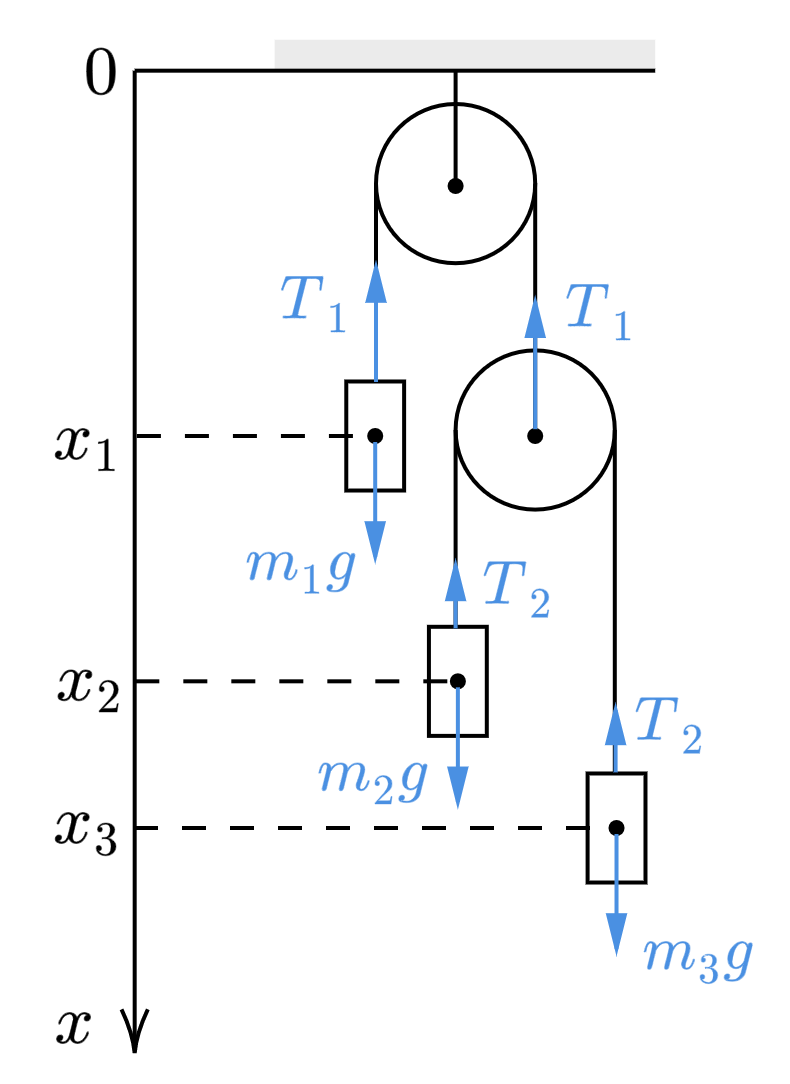
Запишем второй закон Ньютона для каждого из грузов:

( ||| ⃗T1+ m1⃗g =m1 ⃗a1 { ⃗T + m ⃗g =m ⃗a ||| 2 2 2 2 ( ⃗T2+ m3⃗g =m3 ⃗a3

где $ai$ – ускорение $i$ -ого груза.
Спроецировав на ось $x$

(| ||{ m1g− T1 =m1a1 | m2g− T2 =m2a2 ||( m3g− T2 =m3a3

Так как нити нерастяжимы, то их длины постоянна, тогда длина нижней нити равна

(x2− xб2)+ (x3− xб2)= l2,

где $xб2$ – координата нежнего блока, $l2$ – длина нити.
Или в приращениях

Δ(x2− xб2)+ Δ (x3− xб2)= Δl2,

так как длина нити постоянна, то $Δl2 = 0$ . Возьмем производную по времени:

Δx2− Δx б2 Δx3− Δx б2 ---Δt-----+ ---Δt-----= 0⇒ v2x− 2vб2x+ v3x = 0,

где $v$ – скорость элемента.
Взяв производную ещё раз, получим:

a2x − 2aбx+ a3x = 0. (1)

Запишем также длину нити верхнего блока:

(x1− xб1)+ (xб2− xб1) =l1,

где $xб1$ – координата верхнего блока, $l1$ – длина нити.
Или в приращениях

Δx1− xб1+ Δxб2− xб1 = Δl1,

при этом координата верхнего блока постоянна, поэтому $Δxб1 = 0$ и $Δl1 = 0$ . Аналогично первому случаю найдем связь ускорений:

a1x+ aб2x = 0.

Подставим в (1)

a2x +2a1x+ a3x = 0.

Спроецируем на вертикальную ось:

a2 = −2a1− a3.

Подставляем в систему уравнений и получаем:

({ m2g− T2 = − 2m2a1 − m2a3 ( m3g− T2 = m3a3

Сложим два последних уравнения с учётом, что $m2 = m3$ :

m g − T +m g− T = −2m a − m a + m a ⇒ g(m + m )− 2T = −2m a . 2 2 3 2 2 1 2 3 3 3 2 3 2 21

По третьему закону Ньютона для нижнего блока:

T = T +T =2T . 1 2 2 2

Тогда получим систему уравнений:

( { m1g− T1 = m1a1 ( g(m2 + m3)− T1 = − 2m2a1

Домножим первое на $2m2$ , а второе на $m1$ :

( {2m2m1g − 2m2T1 = 2m2m1a1 ( m1g (m2 + m3)− m1T1 =− 2m2m1a1

Сложим и получим:

3m1m2 + m1m3 3 кг⋅3 кг⋅2 кг+ 3 кг⋅2 кг 2m2m1g +m1m2g + m1m3g = T1(2m2 + m1)⇒ T1 =--m1-+-2m2---g =------3 кг-+2-⋅2-кг-----⋅10 Н/кг ≈ 34,3 Н

______________________________________________________________________________________________________________________________________________________________________

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго и третьего законов Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона, третий закон Ньютона, получено уравнение кинематической связи координат и ускорений тел системы).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 45#19941Максимум баллов за задание: 4

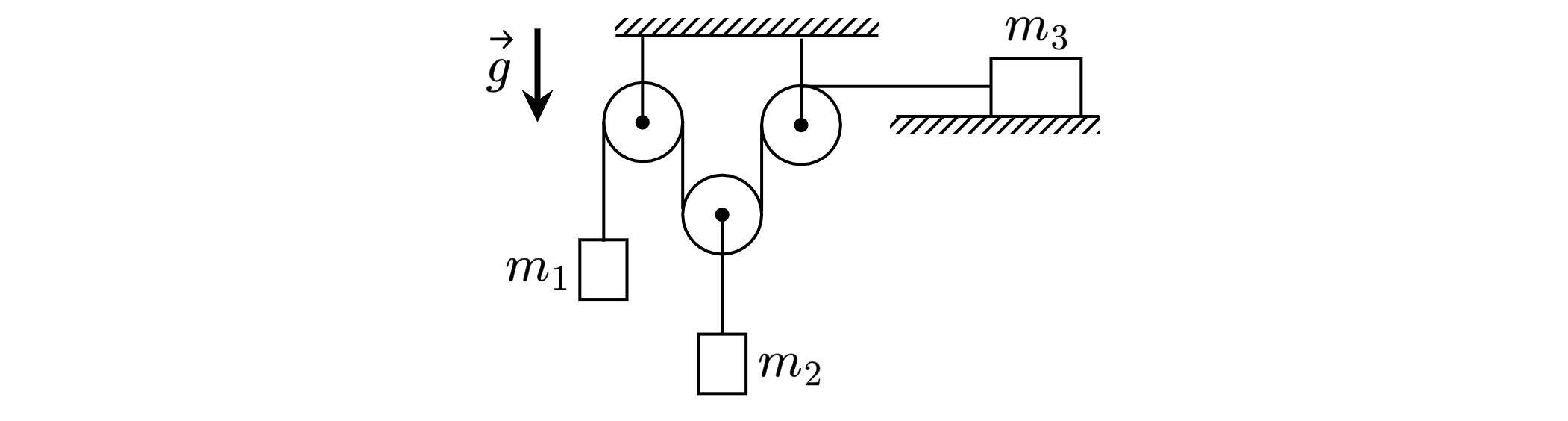
В системе, изображённой на рисунке, массы грузов равны $m1 = 1$ кг, $m2 = 2$ кг, груз массой $m3 = 3$ кг находится на гладкой горизонтальной плоскости, нить невесома и нерастяжима, блоки невесомы, трения нет. Найдите модуль ускорения груза $m2$ . Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

Пусть сила натяжения нитей $T1$ и $T2$ соответственно (см. рис.). Направим ось $x$ и $y$ , как показано на рисунке.

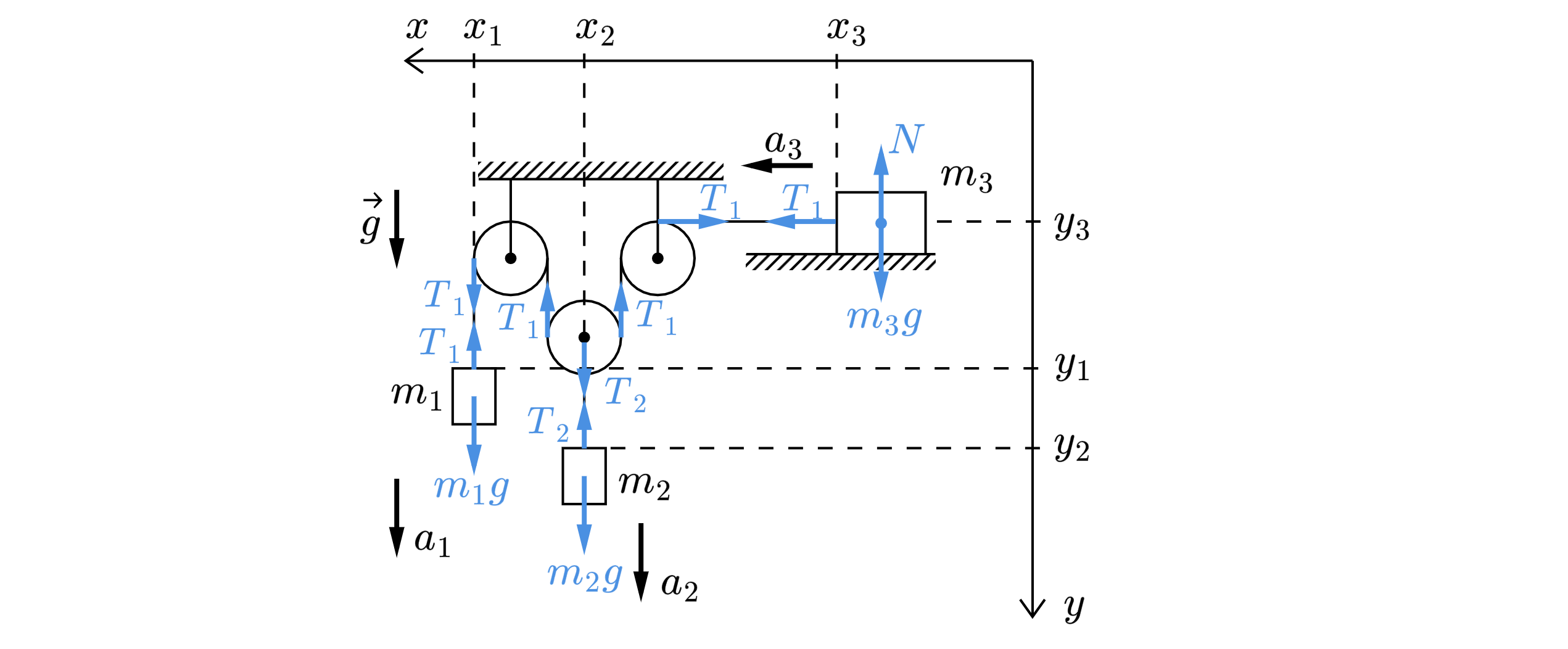
Запишем второй закон Ньютона для каждого из грузов:

( ||| ⃗T1+ m1⃗g = m1⃗a1 { ⃗T + m ⃗g = m ⃗a ||| 2 2 2 2 ( ⃗T3+ m3⃗g +N⃗= m3 ⃗a3

где $ai$ – ускорение $i$ -ого груза, $N$ – сила реакции опоры стола.
По третьему закону Ньютона для среднего подвижного блока

T = T + T = 2T 2 1 1 1

Спроецировав на ось $y$ и $x$ уравнения системы

(|| y m g− T = m a |{ 1 1 1 1 || y m2g− 2T1 = m2a2 |( x T1 = m3a3

Так как нить нерастяжима, то

(x1− x3)+ 2(y2− y3)+ (y1− y3)= const.

Так как $x1$ , $x2$ , $y3$ не изменяются, то продифференцировав, получим

− v3x +2v2y + v1y = 0⇒ −a3x+ 2a2y + a1y = 0

Спроецируем на оси:

−a3+ 2a2+ a1 = 0⇒ a3 = 2a2 +a1

Подставив в систему, получим

( { g− 3(2a2+ a1)= a1 ( 2g− 6(2a2+ a1)= 2a2

Или

({ ({ g− 6a2− 3a1 = a1 ⇒ g− 6a2 = 4a1 ( 2g− 12a2 − 6a1 = 2a2 (2g− 14a2 = 6a1

Домножим на 1,5 первое уравнение и вычтем уравнения:

1,5g− 9a = 2g− 14a ⇒ a = g-= 1 м/ с2 2 2 2 10

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго закона Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатные оси, скорость и ускорение записаны через производные от координаты и скорости по времени, получено уравнение кинематической связи).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 46#19942Максимум баллов за задание: 4

Найдите модуль ускорения $A$ груза массой $M$ в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза $m$ , ускорение свободного падения равно $g$ . Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

Введем ось $X$ так, как показано на рисунке.

На рисунке отмечены координаты блоков $m$ и $XM$ (см. рис.). Также расставим силы для каждого из блоков (пронумерованы). Левая нить натянута с силой $T$ , средняя с силой $2T$ , а правая с силой $4T$ (из-за невесомости нитей и блоков и отсутствия трения).
Запишем второй закон Ньютона для каждого из грузов:

({ ⃗ ⃗ M A= M ⃗g+ T ( m⃗a =m ⃗g+ 4⃗T,

где $A$ и $a$ – ускорения тел массами $M$ и $m$ соответственно.
Спроецируем на вертикальную ось:

({ MA = Mg − T ( ma = mg− 4T

Найдем длину синей и красной нитей.

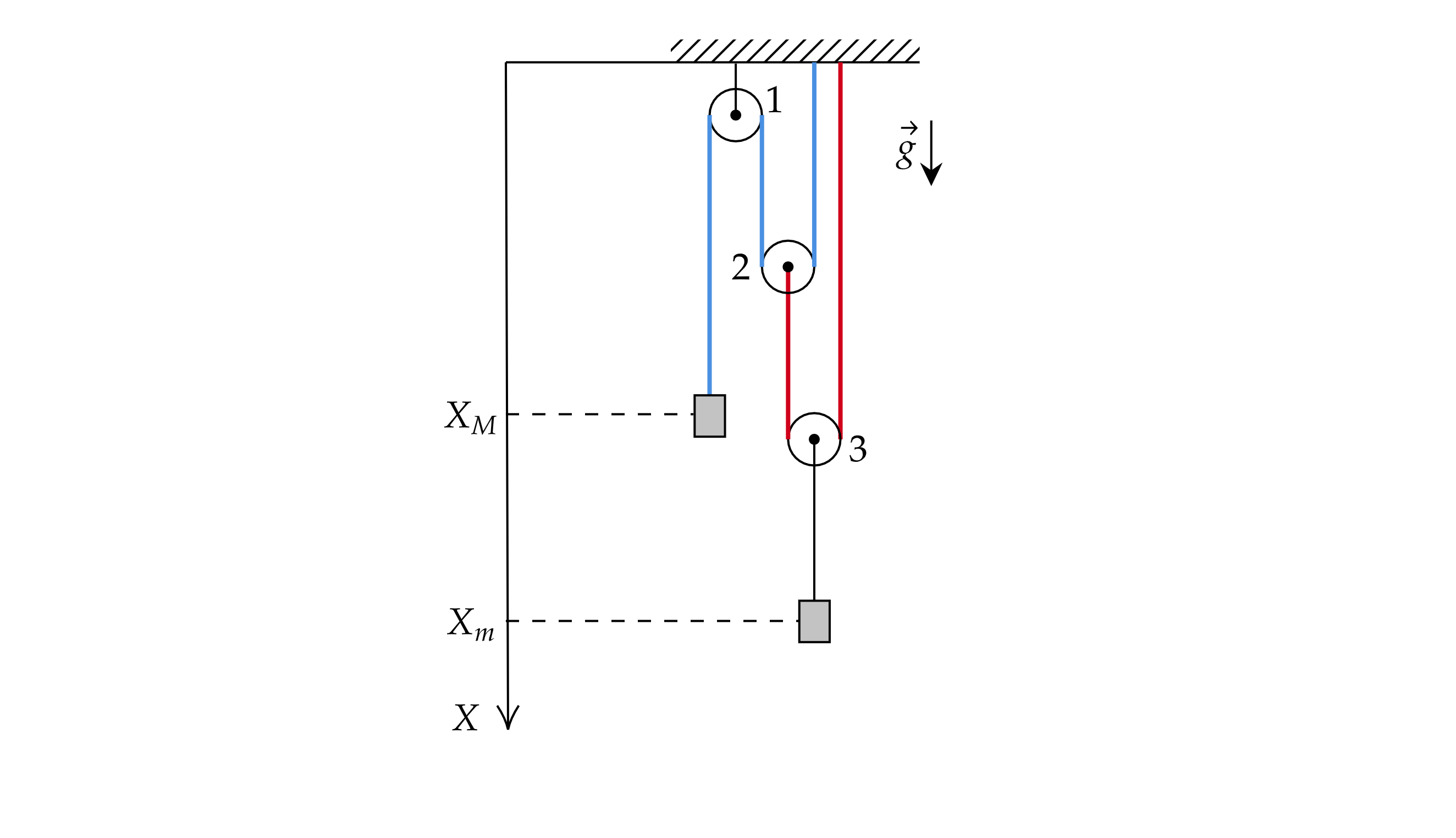
Для синей нити:

(XM − x1)+ (x2− x1)+ (x2− x1)= l1.

Так как $x1 = const$ , то в приращениях:

ΔxM − Δx1+ Δx2 − Δx1+ Δx2 − Δx1 = Δl1 = ΔxM +2Δx2 = Δl1.

Возьмём дважды производную:

Ax +2a2x = 0.

Аналогично для красной нити:

(x3− x2) +(x3− 0)= l2.

Опять же в приращениях:

Δx3 − Δx2+ Δx3 = Δl2

и, взяв производную:

2a3x− 2a2x = 0.

При этом $a3 = am = a$ . Тогда ускорения грузов связаны формулой:

A + 4a= 0.

Подставим во второй закон Ньютона

({ 4MA = 4Mg − 4T (− m A-= mg− 4T 4

Вычитая, получаем

mA 4g(4M − m) 4MA − -4- =4Mg − mg ⇒ A =-16M--+m--

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго закона Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатные оси, скорость и ускорение записаны через производные от координаты и скорости по времени, получено уравнение кинематической связи).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 47#19987Максимум баллов за задание: 4

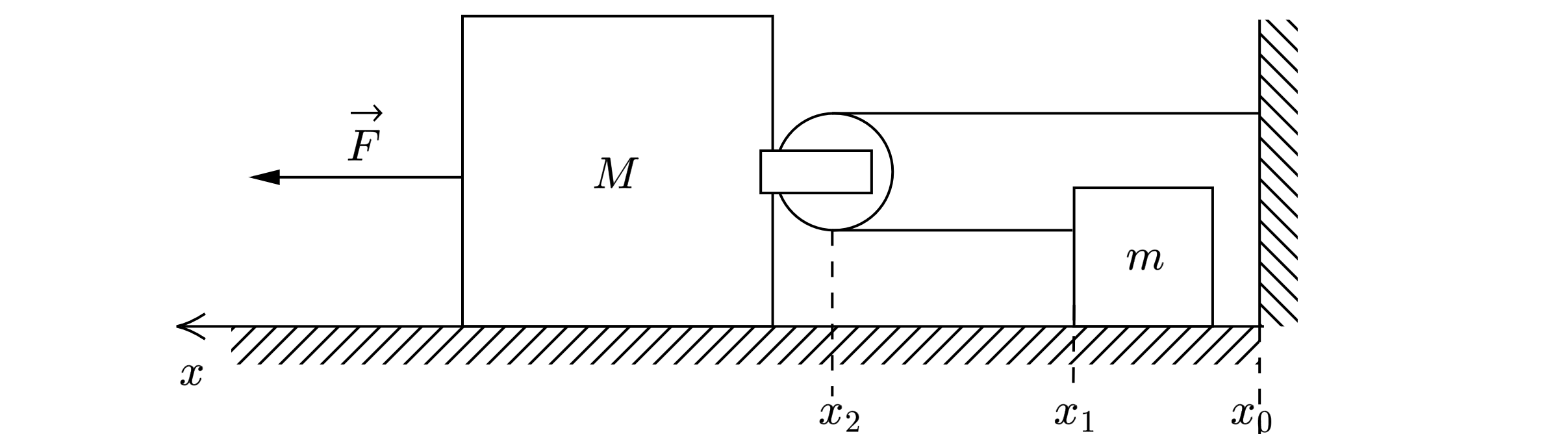
Система из двух грузов массами $M$ и $M ∕2$ , к которым прикреплены легкие блоки, движется по гладкому горизонтальному столу под действием силы $F$ (рис.). С каким ускорением движется точка нити, к которой приложена сила? Масса нити очень мала. Свободные куски нити считать горизонтальными, растяжением нити пренебречь. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

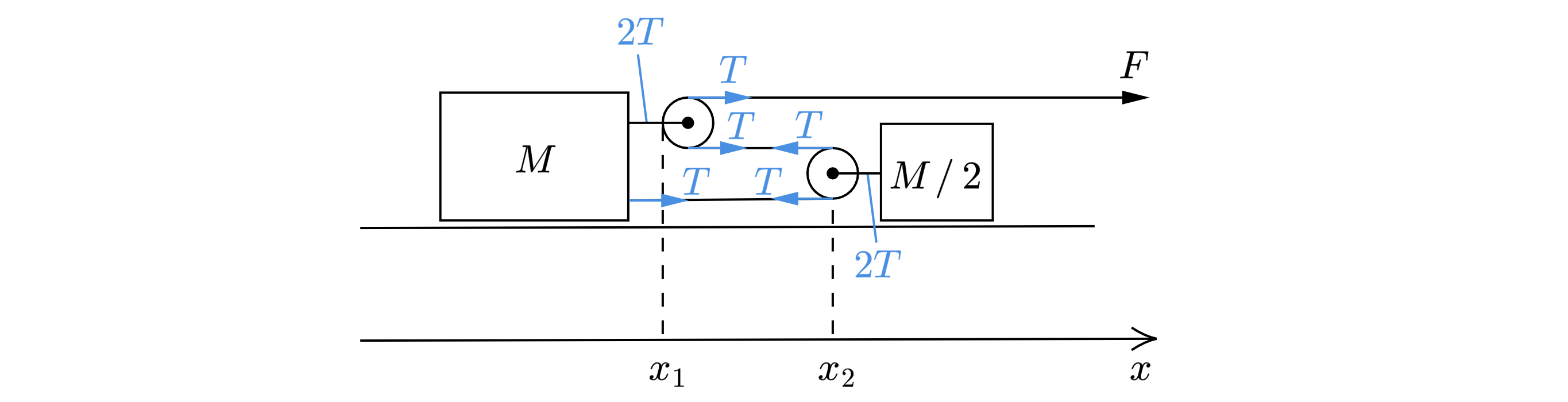
предположим, что в результате движения левый брусок (а значит, и закрепленный на нём конец нити) сместился на $Δx1$ вправо, а правый – на $Δx2$ влево. Ввиду нерастяжимости нити её незакреплённый конец сместился на расстояние

Δl = Δx1 +2Δx2 + 2Δx1.

на $Δx1$ – нижний коней, прикрепленный к $m$ , $2Δx2$ – нижний блок, $2Δx1$ – верхний блок.
Продифференцировав уравнение два раза по времени и обозначив ускорение незакреплённого конца нити за $a$ , получим его связь с ускорениями брусков.

a= 3a1+ 2a2

Запишем второй закон Ньютона на ось $x$

(| ||{ T = F | 3T =ma1 ||( 2T =m ∕2a2

Тогда

3F 4F a1 =-m- a2 = m-.

a = 33F-+24F-= 17F-. m m m

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго закона Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатные оси, скорость и ускорение записаны через производные от координаты и скорости по времени, получено уравнение кинематической связи).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 48#27107Максимум баллов за задание: 4

К бруску массой $M =2$ кг прикреплён лёгкий блок (см. рисунок), через него переброшена лёгкая нерастяжимая нить, один конец которой привязан к стене, а к другому прикреплено тело массой $m = 0,75$ кг. На брусок действует сила $F = 10$ Н. Определите ускорение бруска. Свободные куски нити горизонтальны и лежат в одной вертикальной плоскости, тела двигаются вдоль одной прямой. Массой блока и нити, а также трением пренебречь. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

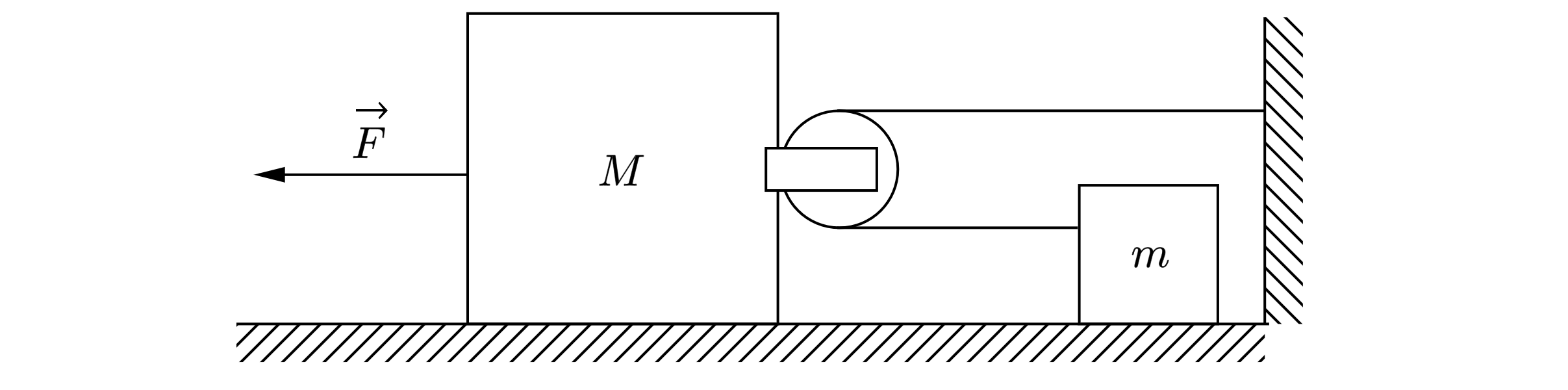
Обоснование

1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).

2. Брусок и тело движутся поступательно, поэтому описываем их моделью материальной точки независимо от их размеров.

3. Из пп. 1 и 2 следует, что движение бруска и тела в ИСО описывается вторым законом Ньютона.

4. Нить невесома, блок идеален (масса блока ничтожна, трения нет), поэтому модуль силы натяжения нити в любой её точке один и тот же.

5. Нить нерастяжима, поэтому модули ускорений подвижного блока и тела $m$ при их прямолинейном поступательном движении отличаются в 2 раза.

Решение

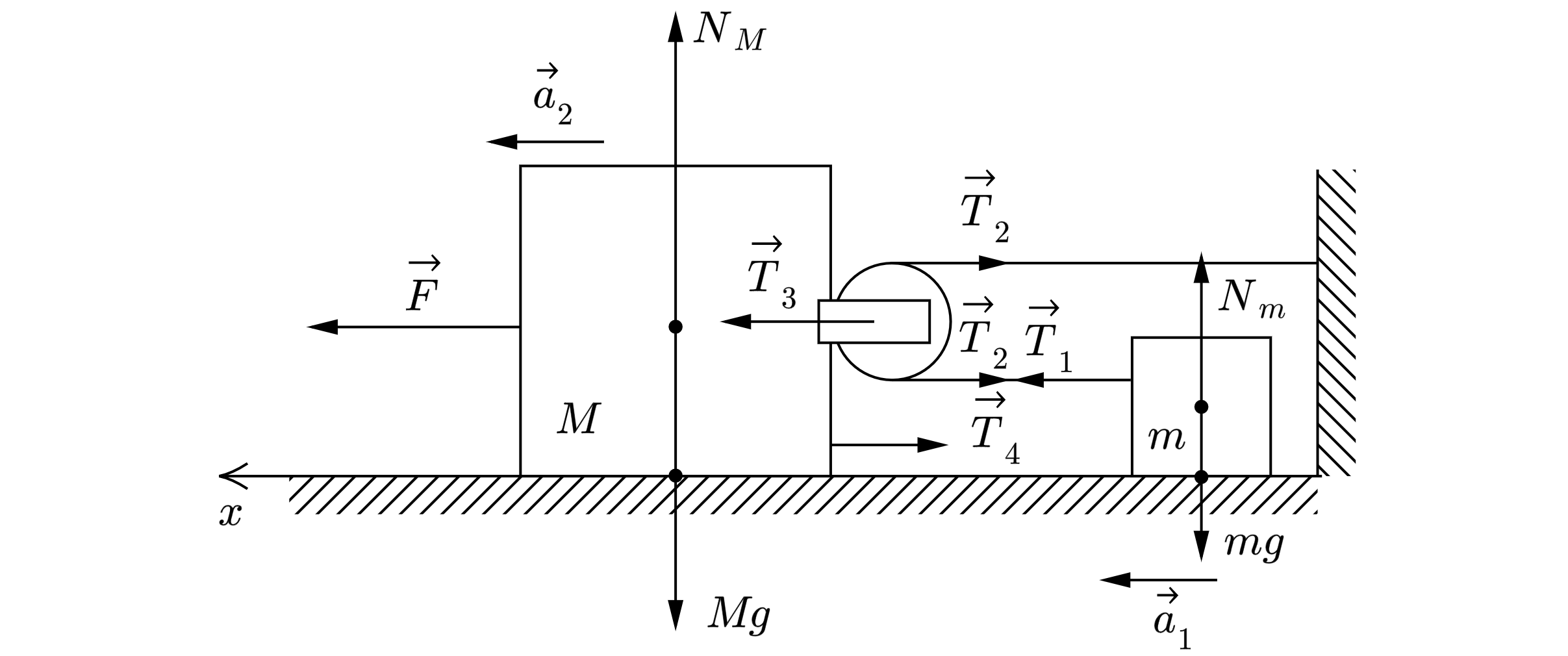
Систему отсчёта, связанную с Землёй, будем считать инерциальной. Запишем второй закон Ньютона в проекциях на горизонтальную ось для тела и бруска: $ma1 = T2;$ $Ma2 = F − T4$ , где $a1$ и $a2$ – ускорения тела и бруска, $T1$ – сила натяжения нити, $T4$ – сила, с которой блок действует на брусок.
Запишем второй закон Ньютона для невесомого блока: $0 = T3− 2T2$ , где $T3$ – сила, с которой брусок действует на блок, $T2$ – сила натяжения нити, действующая на блок.
Поскольку нить невесома, то $|⃗T1|= |⃗T2|= T$ . По третьему закону Ньютона $⃗T3 = − ⃗T4,$ или $|T⃗3|= |T⃗4|.$
Ускорение подвижного блока, а значит, и бруска массой $M,$ в 2 раза меньше ускорения тела массой $m,$ так как за одно и то же время перемещение тела в 2 раза больше перемещения бруска: $a1 = 2a2.$
Приходим к системе уравнений:

({ F − 2T = Ma2 ( T =m ⋅2a2,

откуда

a2 =--F2---= -----10 Н-----= 2 м/с2 M + 4m 2 кг+ 4⋅0,75 кг

Альтернативное решение

Расставим силы, действующие на тела

Здесь $Nm$ и $NM$ – силы реакции поверхности, действующие на тело и брусок, соответственно, $a1$ и $a2$ – ускорения тела и бруска, $T1$ – силы натяжения нити, $T4$ – сила, с которой блок действует на брусок. Поскольку нить невесома, то $|T⃗1|= |T⃗2|= T$ . По третьему закону Ньютона $|T3|=|T4|.$ Также по второму закону Ньютона для блока $2T2 = T3 ⇒ T3 = 2T.$
Запишем второй закон Ньютона для тела и бруска:

T⃗1 +m ⃗g+ N⃗m = m ⃗a1

⃗ ⃗ ⃗ F + T4+ M ⃗g+ NM = M ⃗a2

Спроецируем вторые закон Ньютона на горизонтальную ось $x$ , с учетом $T = T 1$ , $T = 2T 4$ :

({ T =ma1 ( F − 2T = Ma2

Для нахождения связи ускорений воспользуемся кинематическими связями.

Длина нити равна:

l = (x2− x1)+(x2− x0)

В приращениях:

Δl = Δ (x2− x1)+ Δ(x2− x0),

Разделим на время $Δt$ и получим производную от координаты, то есть скорость, при этом $Δl Δt-= 0$ из-за постоянства длины нити и $Δx0-= 0 Δt$ из-за того, что координата $x0$ постоянна.

0 = v2 − v1+ v2,

аналогично, взяв производную ещё раз получим связь ускорений:

2a = a . 2 1

Вернемся к системе уравнений с учётом связи ускорений:

({ ({ T =m ⋅2a2 ⇒ 2T = 4ma2 ( F − 2T = Ma2 ( F − 2T = Ma2

Отсюда

--F---- -----10 Н----- 2 a2 = M + 4m = 2 кг+ 4⋅0,75 кг = 2 м/с

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета

2. Обоснована возможность применения к телам модели материальной точки

3. Обосновано применение второго закона Ньютона для описания движения тел

4. Обосновано равенство сил натяжения нитей

______________________________________________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

________________________________________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатную ось, третий закон Ньютона, уравнения кинематической связи для координат тел, их скоростей и ускорений).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

________________________________________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

________________________________________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ответ:

$--F---- 2 a2 = M + 4m = 2 м/с$

Ошибка.
Попробуйте повторить позже

Задача 49#47217Максимум баллов за задание: 4

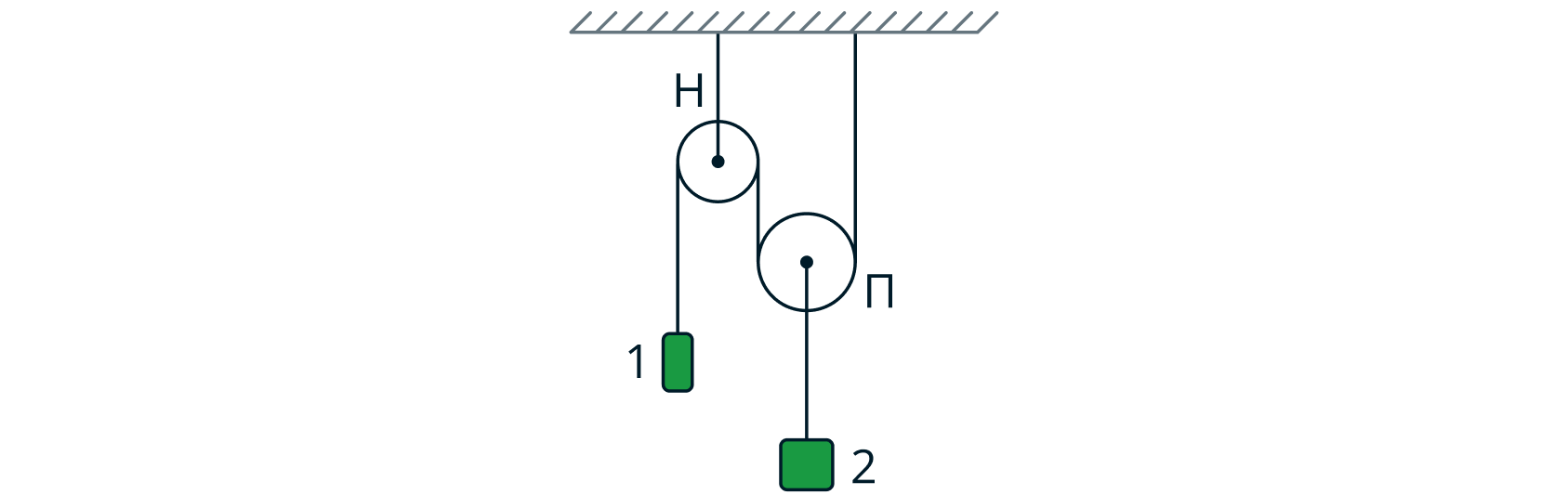
Два подвешенных на нитях груза 1 и 2 различной массы могут двигаться в системе, состоящей из неподвижного блока Н и подвижного блока П (см. рис.).
1) Найти отношение масс грузов 1 и 2, если подвешенные грузы остаются неподвижными.
2) Найти отношение масс грузов 1 и 2, если груз 1 движется с ускорением $a1 =g∕5$ , направленным вверх.
Массами нитей, блоков, а также трением в осях блоков можно пренебречь
(«Физтех», 2018, 9)

$PIC$

Показать ответ и решение

Пусть сила натяжения нити у груза 1 равна $T$ . Расставим силы, действующие на нити и грузы. По третьему закону Ньютона сила натяжения нити у подвижного равна $2T$ (см. рис.)

$PIC$

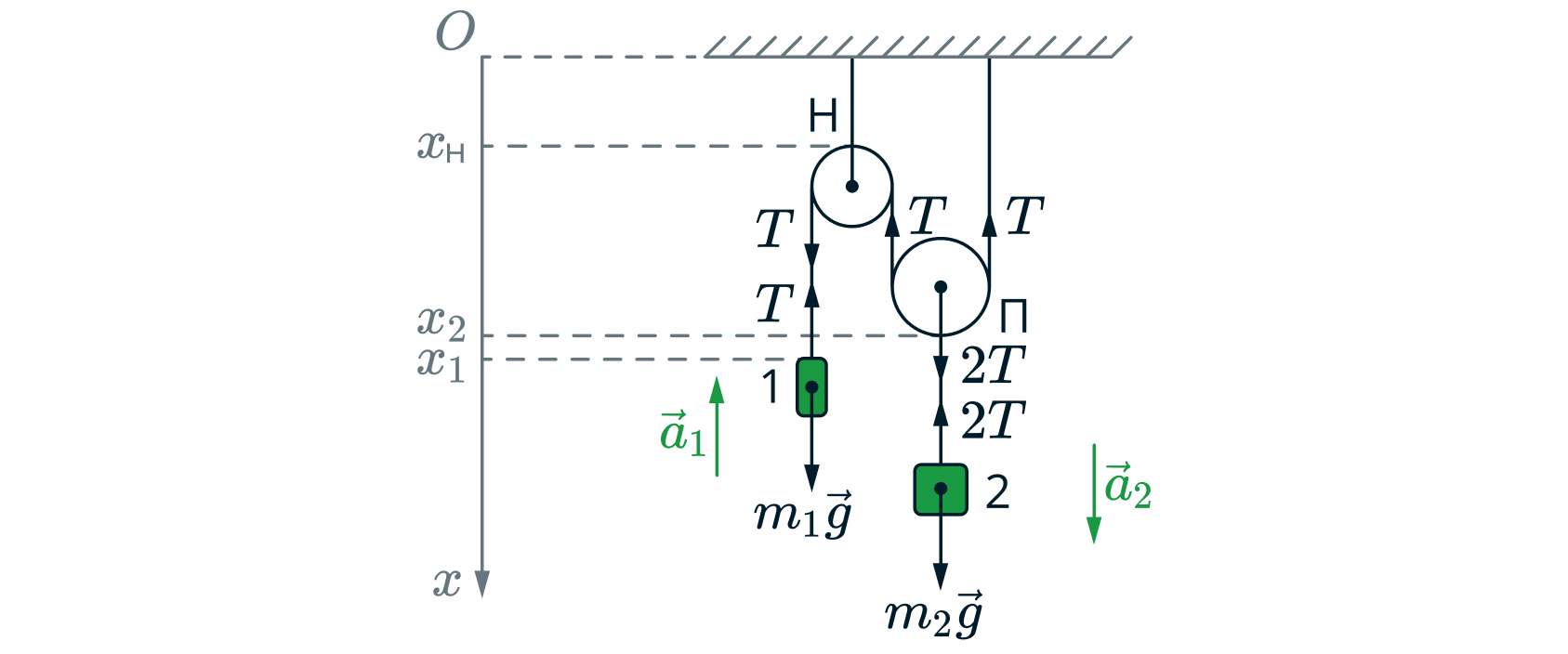
Запишем второй закон Ньютона для груза 1:

⃗T + m1⃗g = m1a⃗1.

Аналогично для второго груза

2⃗T + m2⃗g = m2⃗a2.

1) Спроецируем вторые законы Ньютона на ось $x$ , с учётом, что тела покоятся ( $a1 = a2 = 0$ ).

T − m1g = 0 2T − m2g = 0 ⇒ m1-= 1. m2 2

2) Спроецируем второй закон Ньютона на ось $x$ :

m1g − T =− m1a1.

m2g− 2T = m2a2.

Из этих двух уравнений получим

m2g − 2m1g = m2a2+ 2m1a2.

Найдём длину нити

(x1 − xн)+ (x2− xн)+(x2− 0)= l.

В приращениях

Δ(x1− xн)+ Δ(x2− xн)+Δ (x2− 0) =Δl.

Разделим на $Δt$ и получим производную

x′1 − x′н +x′2 − x′н +x′2− 0′ = const′ ⇒ v1x− 0+ v2x− 0+ v2x− 0 =0

Аналогично, взяв вторую производную, получим связь ускорения грузов:

′ ′ ′ ′ v1x +v2x+ v2x = 0 ⇒ a1x + 2a2x = 0 ⇒ a1x = −2a2x.

С учётом проекции на направленность ось связь модулей ускорений: $a1 = 2a2$ . Тогда

m2 g m1 3 (m2− 2m1)g = (2m1 + 2-)a1 ⇒ (2m2 − 4m1 )g = (4m1 + m2)5 ⇒ m2-= 8.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 50#47218Максимум баллов за задание: 4

Три одинаковых груза массой m соединены c помощью идеальных нитей и двух идеальных блоков, как показано на рисунке. Найдите величину и направление ускорения нижнего груза.

Показать ответ и решение

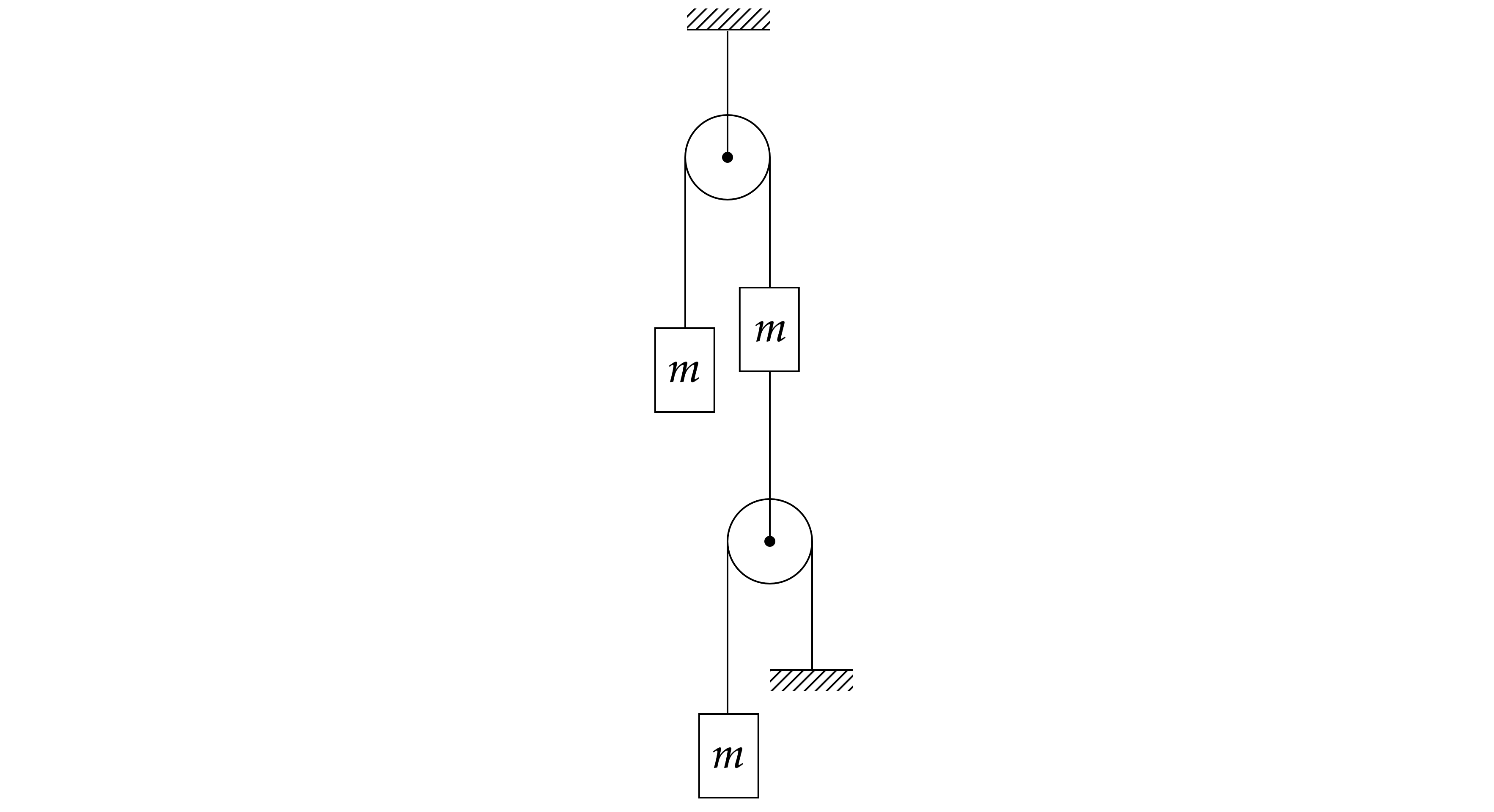
Пусть натяжение нижней верёвки равно $T$ , $T1$ – натяжение части верхней веревки между грузами, $T2$ – натяжение части верхней веревки между грузом и нижним блоком. Расставим силы

Запишем второй закон Ньютона для всех грузов

( |||1 m⃗g +T⃗= m ⃗a1 {2 m⃗g +T⃗ = m⃗a ||| 1 2 (3 m⃗g +T⃗2 +T⃗1 = m⃗a3

Поскольку блоки невесомы, сумма сил, приложенных к нижнему блоку, равна нулю, то есть $T2 = 2T$ . Спроецируем второй закон Ньютона на ось $x$ :

(| ||{1 mg − T = ma1 |2 mg − T1 = −ma2 ||(3 mg +T2 − T1 = ma3

Ускорения верхних грузов и подвижного блока равны. Пусть они равны $a$ . Найдём длину нижней нити

(x3− xб)+ (x2− xб)= l.

В приращениях

Δ(x3− xб)+ Δ(x2− xб) =Δl.

Разделим на $Δt$ и получим производную

x′3− x′б+ 0− x′б = 0 ⇒ v3x − vбx− vбx = 0

Аналогично, взяв вторую производную, получим связь ускорения грузов:

′ ′ ′ ′ v3x− vбx− vбx =0 ⇒ a3x− 2aбx = 0⇒ a3x =2aбx.

С учётом проекции на ось $x$ , получаем связь модулей ускорений $a2 = a3 = aб =a.$ , $a1 = 2a$ . Запишем второй закон Ньютона

( |||{1 mg − T = 2ma 2 T − mg = ma ||| 1 (3 mg + 2T − T1 = ma

Сложим два последних уравнения системы:

({mg − T =2ma ⇒ a = g (2T = 2ma 3

С учётом связи ускорений $a1 = 2a =2g∕3.$

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 51#53845Максимум баллов за задание: 4

Найдите модуль и направление ускорения, с которым нужно двигать конец нити для того, чтобы правый груз, имеющий массу $m = 3$ кг, оставался неподвижным. Массой нити и блоков можно пренебречь. Нить нерастяжима, трение отсутствует. Ускорение свободного падения принять равным $g = 10$ м/с $2.$
(Всеросс., 2018, МЭ, 10)

Показать ответ и решение

Расставим координаты грузов и силы, действующие на них.

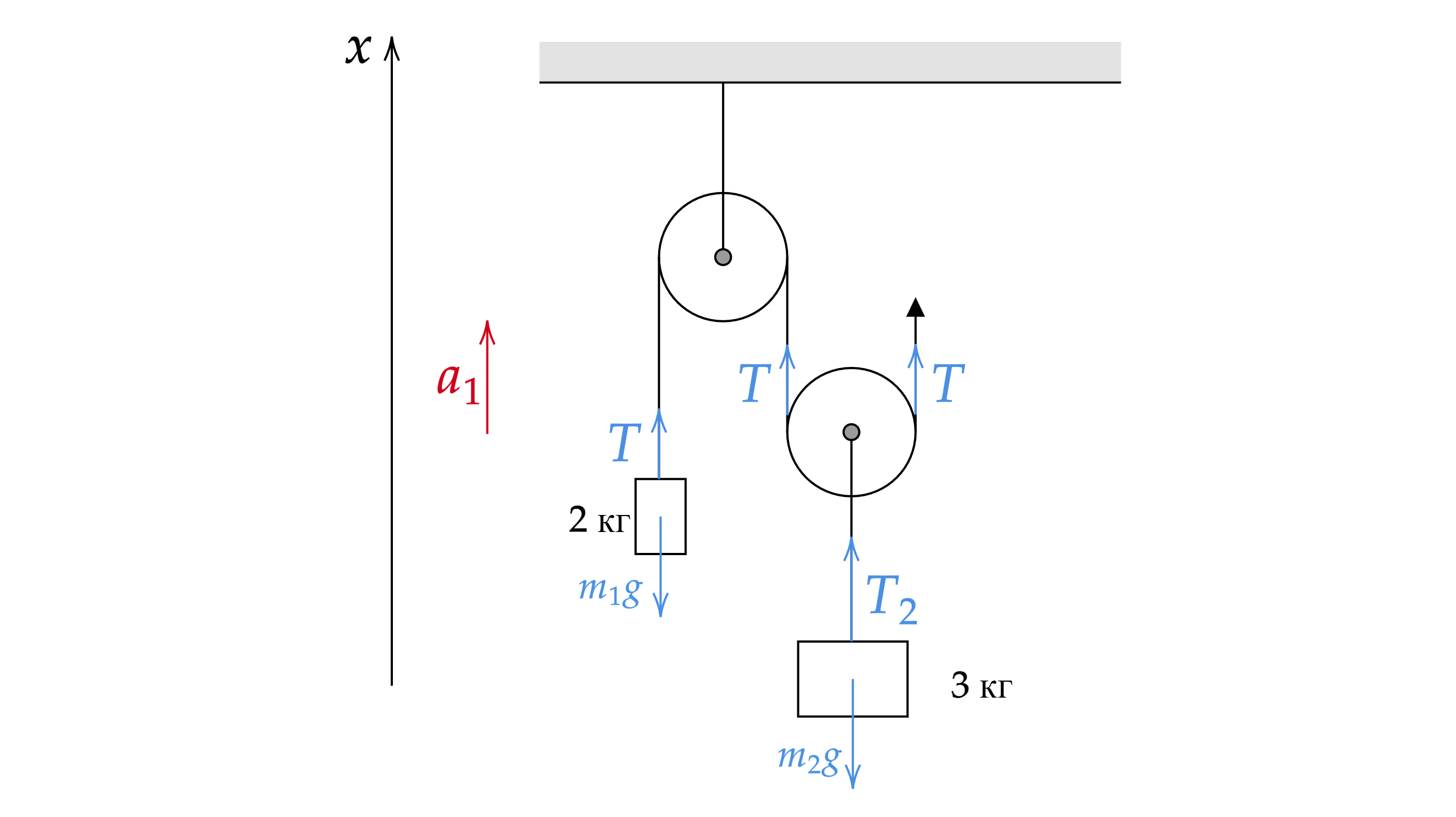
Запишем второй закон Ньютона для каждого из тел:

⃗T + m1⃗g = m1a⃗1,

⃗T2+ m2⃗g =m2 ⃗a2,

где $a1$ – ускорение левого груза (нити), $a2$ – ускорение правого груза.
Из третьего закона Ньютона $T2 = 2T$ . По условию $a2 = 0$ . Спроецируем второй закон Ньютона на ось $x$ :

T − m1g = m1a1 T2− m2g =0.

Тогда

T − m1g = m1a1 2T = m2g

Значит

m2g- 2 − m1g = m1a1

тогда искомое ускорение

m2 3 кг 3 g 10 Н/кг a1 = 2m1-g− g = 2⋅2-кгg− g = 4g − g = −4 = −-4-= − 2,5 Н/кг

Так как ускорение отрицательно, то первоначально ускорение направлено неверно, значит, ускорение должно быть направлено вниз и быть равно 2,5 м/с $2.$

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 52#53846Максимум баллов за задание: 4

В системе, изображенной на рисунке, нить невесома и нерастяжима, блоки невесомы, трение отсутствует. Массы грузов равны $m1 = 2$ кг и $m2 = 4$ кг. Найдите модуль ускорения оси блока $A$ , к которой приложена в вертикальном направлении сила $F = 16$ Н. Ускорение свободного падения принять равным $g =10$ м/с $2.$

Показать ответ и решение

Расставим координаты грузов и силы, действующие на них.

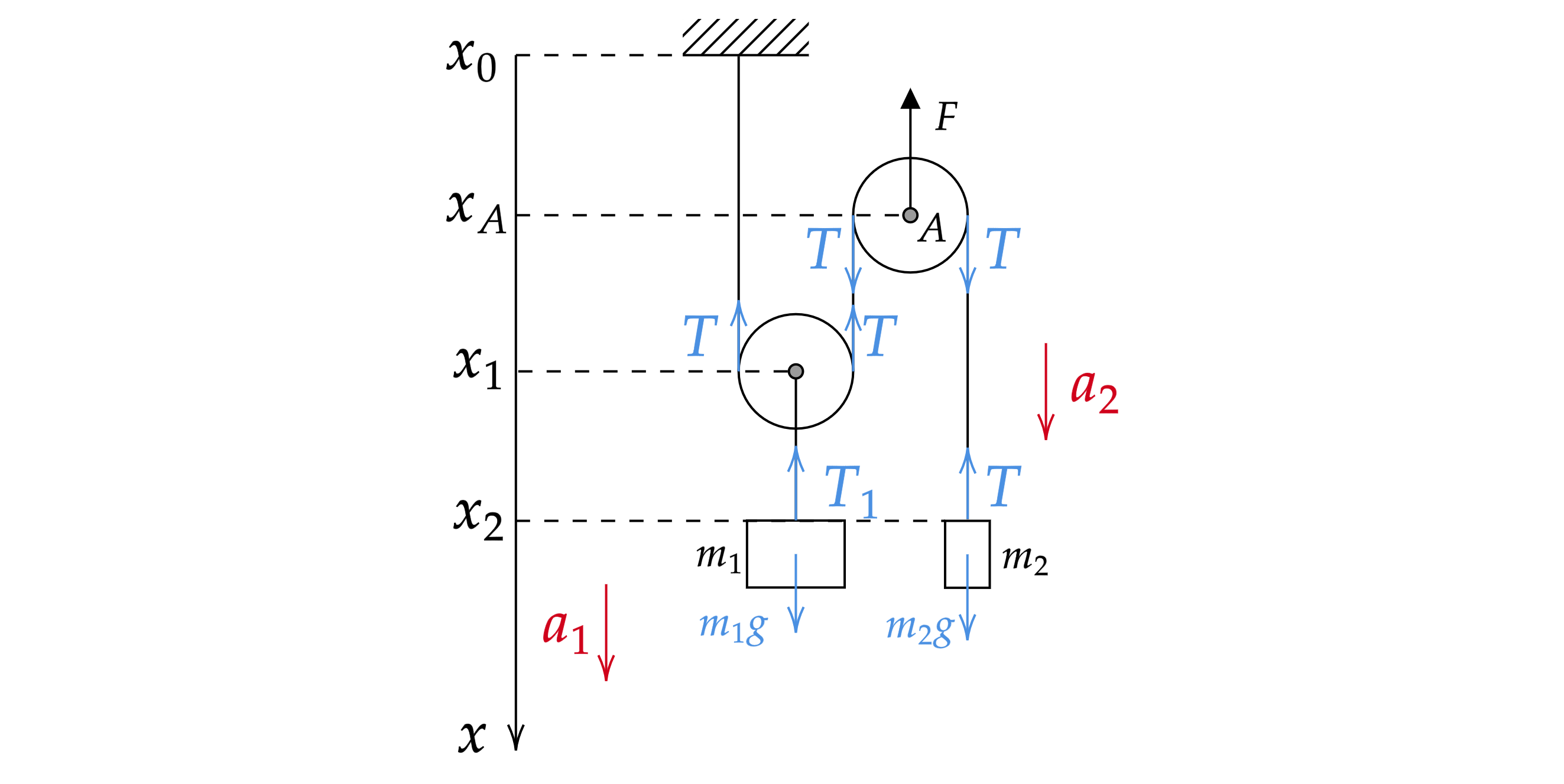
По третьему закону Ньютона $F = 2T$ и $T1 = 2T$ .
Запишем второй закон Ньютона для каждого из тел:

⃗T1+ m1⃗g =m1 ⃗a1,

⃗T + m2⃗g = m2a⃗2,

Спроецируем второй закон Ньютона на ось $x$

m1g − T1 = m1a1 m2g− T = m2a2,

с учётом третьего закона Ньютона

m1a1 = m1g− F m2a2 = m2g− F-. 2

Длина нити равна

(x1− x0)+ (x1− xA)+ (x2− xA)= l

В приращениях

Δx1 − Δx0 + Δx1− ΔxA + Δx2 − ΔxA = Δl,

при этом $l = const$ , $x0 = const$ , значит, приращение равно нулю. Разделим на $Δt$

Δx1- Δx1- Δx2- ΔxA- Δt + Δt + Δt − 2 Δt = 0.⇒ 2v1+ v2 = 2vA.

Аналогично получим связь ускорений:

2a1+ a2 = 2aA

Из вторых законов Ньютона

F F a1 =g − m1- a2 = g− 2m2-.

Подставим в связь ускорений:

aA = a1+ a2 =g − F-+ g− -F--= 3g − (m1-+-4m2)F-= 3⋅10 м/с2 − (2-кг+-4⋅4 кг)16 Н-= 6 м/с2 2 m1 2 4m2 2 m1m2 2 4⋅2 кг⋅4 кг

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 53#53848Максимум баллов за задание: 4

В системе, показанной на рисунке, массы грузов равны соответственно $m1 = m3 = m = 0,1$ кг, $m2 = 3m$ . Первоначально систему удерживают, затем отпускают. Грузы приходят в движение. Начальные скорости всех грузов нулевые. Ускорение свободного падения $g = 10$ м/с $2.$ Массы блоков и нитей по сравнению с массой грузов пренебрежимо малы. Нерастяжимые нити свободно скользят по блокам.
1. Найдите скорость $V1$ груза 1 в тот момент, когда груз 2 опустится на $H =0,5$ м.
2. Найдите силу $T2$ натяжения нити, на которой подвешен груз 2
(«Физтех», 2019, 9)

Показать ответ и решение

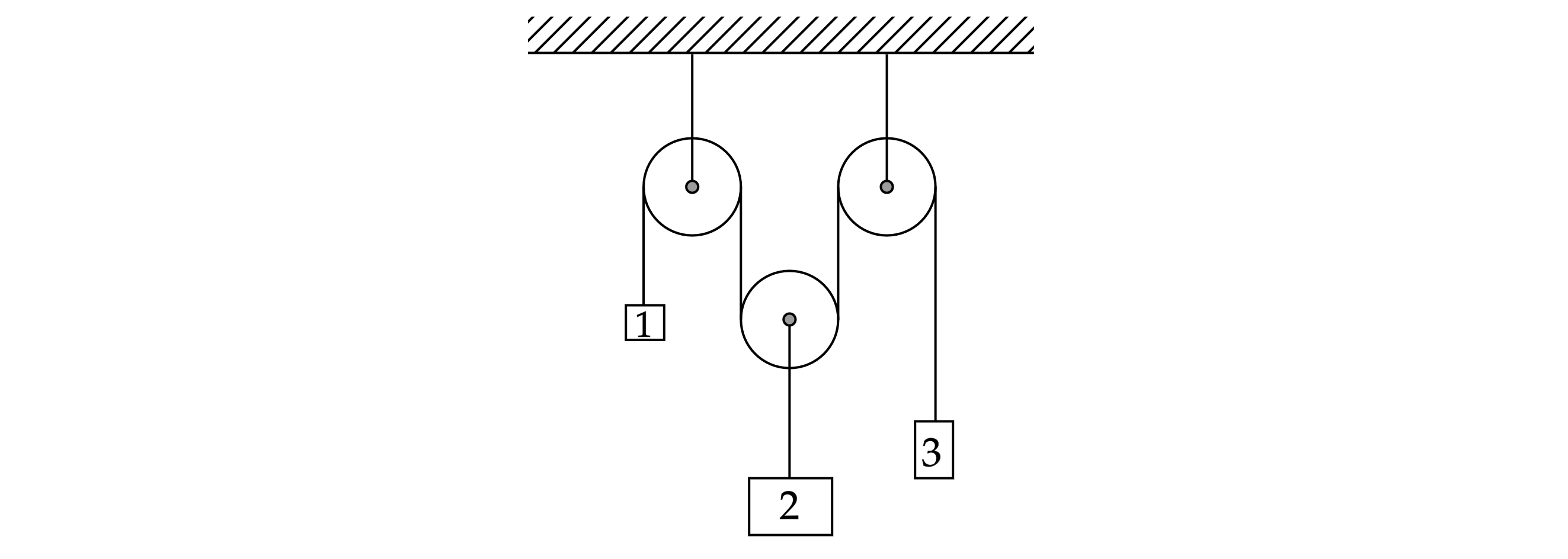
Расставим координаты грузов и силы, действующие на них.

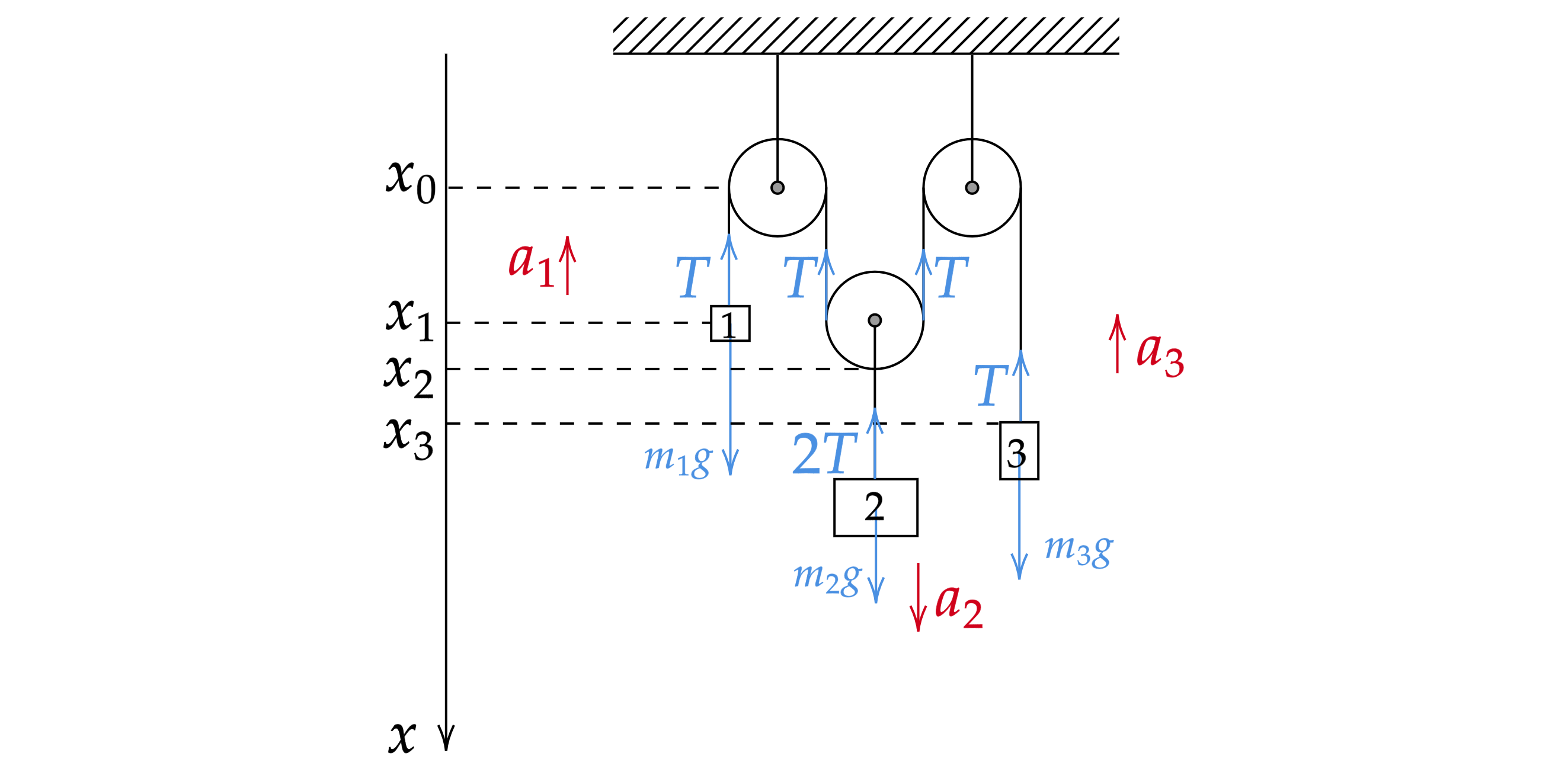
Запишем второй закон Ньютона для каждого из тел:

⃗T + m1⃗g = m1a⃗1,

⃗T2+ m2⃗g =m2 ⃗a2,

⃗T + m3⃗g = m3a⃗3.

Из третьего закона Ньютона $T2 = 2T$ , тогда в проекции на ось $x$ вторые законы Ньютона можно переписать в виде:

m1g − T =− m1a1,

m2g− 2T = m2a2,

m3g − T =− m3a3.

Так как $m1 = m2 =m$ , то $a1 = a3$ . Значит, при подъёме они имеют одинаковые скорости и проходят одинаковые расстояния Найдем длину нити:

(x1 − x0)+ (x2− x0)+ (x2− x0)+ (x3− x0)= l.

В приращениях

Δx1 +2Δx2 + Δx3− 3Δx0 = Δl

Так как $x = const 0$ и $l = const$ , то $Δx = 0 0$ и $Δl =0$ . Значит

2Δx2 +Δx1 + Δx3 = 0.⇒ 2Δx2 = −(Δx1 + Δx3)

Найдем производную (поделим на приращение $Δt$ ).

Δx2 Δx1 Δx3 2-Δt-+ Δt--+ Δt--= 0.

Пусть скорости 1 и 3 грузов равны $v$ , а скорость второго груза $v2$ , тогда

2v2x+ vx + vx = 0⇒ v2x = −vx.

Значит, скорость второго груза равна скорости 1 и 3, но обратна по направлению.
Аналогично получим связь ускорений

Δv2x = − Δvx-⇒ a2x = − a. Δt Δt

То есть ускорение второго груза равно ускорениям 1 и 3 грузов, но обратно по направлению.
Так как грузы 1 и 3 проходят одинаковые расстояния, то $Δx1 = Δx3 = H$ . Запишем закон сохранения энергии, для этого нулевой уровень потенциальной энергии для каждого из грузов возьмем за начальное положение, тогда

---- -------------- (m1+-m2-+-m3)v21- 5mv21- ∘ 2 ∘ 2 0= m1gH+m3gH −m2gH+ 2 ⇔ 0 =mgH+mgH −3mgH+ 2 ⇒ v1 = 5gH = 510 Н/ кг⋅0,5 м≈ 1,4 м/с

2) Из проекций вторых законов Ньютона

3mg − 2T = 3ma 2mg − 2T = −2ma

следует

mg = 5ma ⇒ a= g. 5

То есть ускорения всех грузов равны $g∕5$ . Тогда сила натяжения нити $T 2$ :

3m-⋅4g 12mg- 12-⋅0,1-кг⋅10-Н/кг 3mg− T2 =3ma ⇒ T2 = 3m(g− a)= 5 = 5 = 5 = 2,4 Н

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 54#60888Максимум баллов за задание: 4

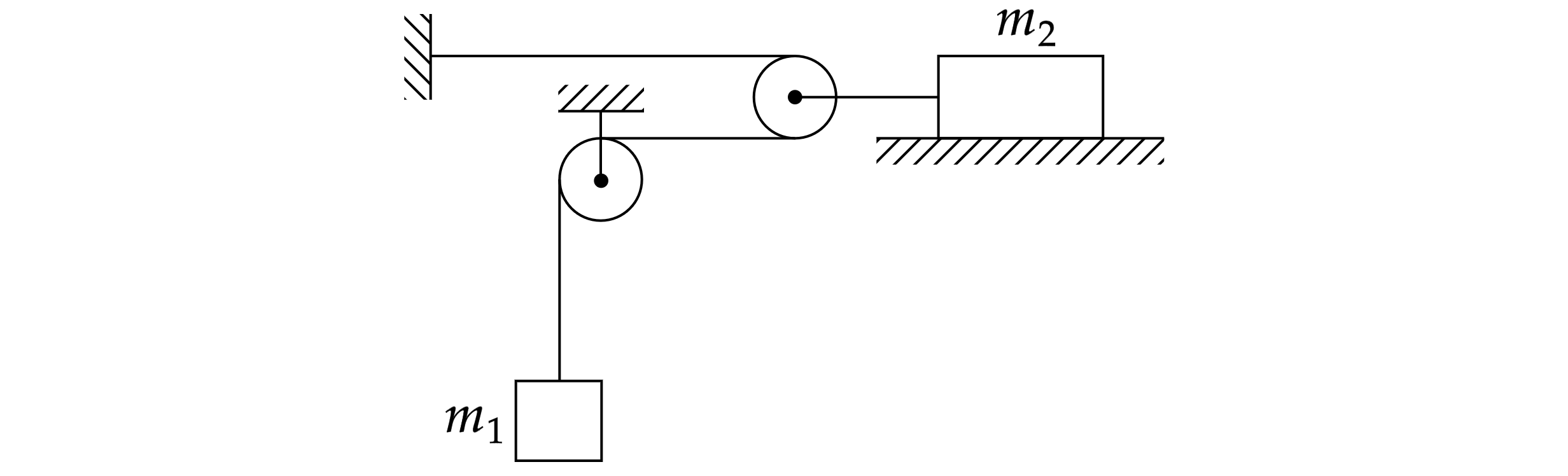
На гладкой горизонтальной поверхности удерживают груз массой $m2.$ Он соединен невесомой и нерастяжимой нитью с грузом массой $m1 = 2 кг$ через систему идеальных блоков (блоки невесомые, трение в осях отсутствует). Участки нитей, не лежащие на блоках, вертикальны или горизонтальны. Груз $m = 4 кг 2$ отпускают и система приходит в движение. Найдите ускорение груза $m1$ в ходе движения. Какие законы Вы использовали для описания движения тел? Обоснуйте их применимость к данному случаю.

$PIC$

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Учитывая, что нить невесома и блок идеальный, делаем вывод, что силы натяжения, приложенные к телам, равны по модулю.

Решение

Введём оси $x$ и $y$ , как показано на рисунке. Также изобразим силы, действующие на грузы.

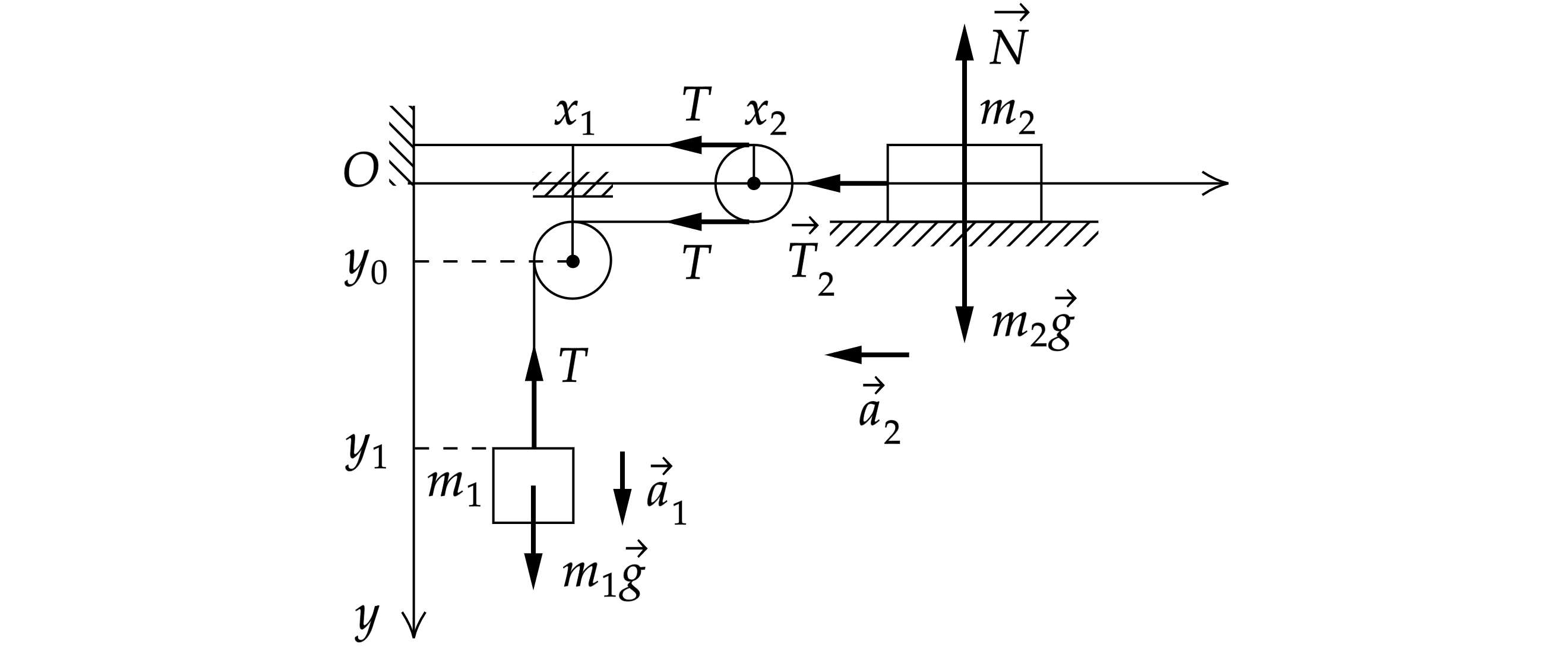
Запишем второй закон Ньютона для $m1$ :

m1⃗g +T⃗= m1 ⃗a1,

где $a1$ – ускорение груза $m1$ .

Спроецируем на ось $y$ :

m1g − T = m1a1

Запишем также второй закон Ньютона для $m2$ :

m2 ⃗g+ ⃗T2 + N⃗ = m2⃗a2,

где $a2$ – ускорение груза $m2$ .

Спроецируем на ось $x$ :

T = m a 2 2 2

По третьем закону Ньютона $T = 2T 2$ , тогда получаем систему уравнений

( { m g − T = m a 1 1 1 ( 2T = m2a2

Найдем длину нити:

l = (x2 − 0)+ (x2 − x1)+ (y1 − y0)

В приращениях

Δl = Δ(x2 − 0)+ Δ (x2 − x1)+ Δ(y1 − y0)

Разделим на приращение времени $Δt$

′ ′ ′ ′ ′ ′ l = x2 + x2 − x1 + y1 − y0,

Так как нить нерастяжима, то $′ l= 0$ , координаты $x1$ , $y0$ постоянны, значит $′ x1 = 0$ и $′ y0 = 0$ . При этом скорость изменения координаты – скорость

′ 0 = 2v2x + v1y

Аналогично получим связь ускорений грузов

Δv2x- Δvy1- 0 = 2 Δt + Δt ⇒ 2a2x + a1y = 0

То есть связь модулей ускорений

a1 a2 =-2

Подставим в систему уравнений

( { m1g − T = m1a1 ( a1 2T = m2-2 .

Отсюда ускорение груза $m1$

m2a1- --4m1g--- 4⋅2 к-г⋅10 Н/-кг 2 2m1g = 2m1a1 + 2 ⇒ a1 = 4m1 + m2 = 4⋅2 кг+ 4 кг ≈ 6,67 м/с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Критерий 1

Верно обоснована возможность испольования законов	1
(закономерностей). В данном случае: выбор ИСО, модель материальной точки, равенство модулей сил натяжения нитей, возможность применения второго закона Ньютона

В обосновании возможности использования законов	0
(закономерностей) допущена ошибка
ИЛИ
Обоснование отсутствует

Критерий 2
Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае - второй закон Ньютона, соотношение между ускорениями связанных тел);
II) описаны вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений величин, используемых
в условии задачи, и стандартных обозначений величин,
используемых при написании физических законов);
III) проведены необходимые математические преобразования
и расчёты (подстановка числовых данных в конечную формулу),
приводящие к правильному числовому ответу (допускается решение
«по частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
фиизческой величины

Правильно записаны все необходимые положения теории,	2
фиизческие законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И(ИЛИ)
В решении имеются лишние записы, не входящие в решение
(возможно, неверные), которые не отделены от решения и не
зачёркнуты
И(ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и(или) в математических преобразованиях/
вычислениях пропущены логически важные шаги.
И(ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерений величины)

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования
с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной
задачи (или в утверждения, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования
с имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 55#78750Максимум баллов за задание: 4

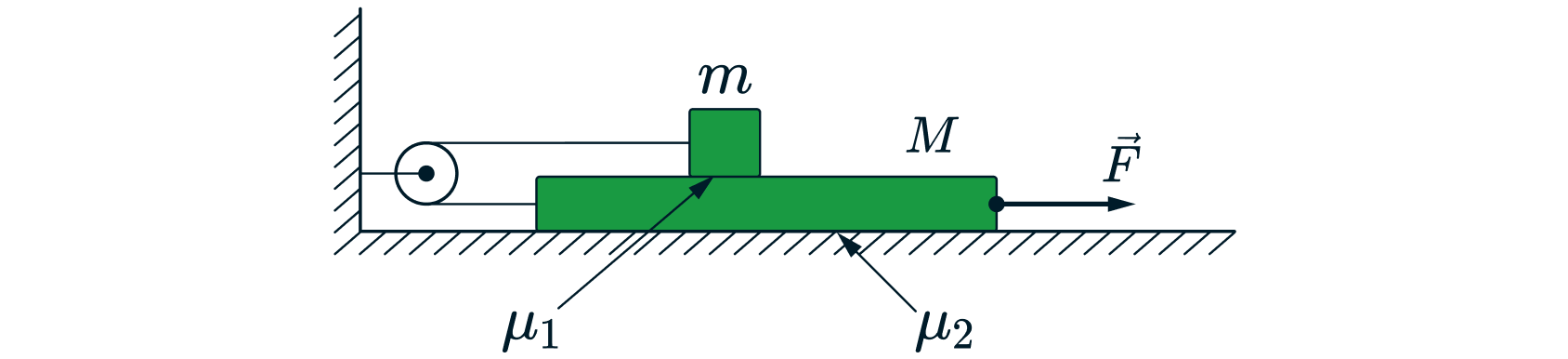
Брусок опирается на массивную горизонтальную доску массы $M = 0,8$ кг, которая лежит на шероховатой горизонтальной плоскости. Брусок и доска связаны невесомой нерастяжимой нитью, перекинутой через невесомый и гладкий блок. Под действием горизонтальной силы $F = 6$ Н доска движется поступательно вправо, в результате чего брусок приобретает ускорение $a = 1$ м/с $2$ . Найдите массу бруска m, если коэффициент трения между бруском и доской $μ1 =0,5$ , а между доской и поверхностью – $μ2 = 0,3$ . Сделайте рисунок, укажите все силы, действующие на груз и доску.

$PIC$

Какие законы Вы использовали для описания движения тел и блоков? Обоснуйте их применимость к данному случаю.

Показать ответ и решение

Обоснование Будем считать систему отсчета, связанную с Землей, инерциальной. И брусок, и доска движутся поступательно, поэтому их движение можно описывать моделью материальной точки. Поэтому для тел в ИСО можно применять законы Ньютона. По условию нить невесома и нерастяжима, блок неподвижный, следовательно, сила натяжения нити, действующая на брусок, равна по модулю силе натяжения нити, действующей на доску, и ускорения обоих тел равны по модулю.

Решение
1) Укажем силы, действующие на брусок (красным) и на доску (синим).

$PIC$

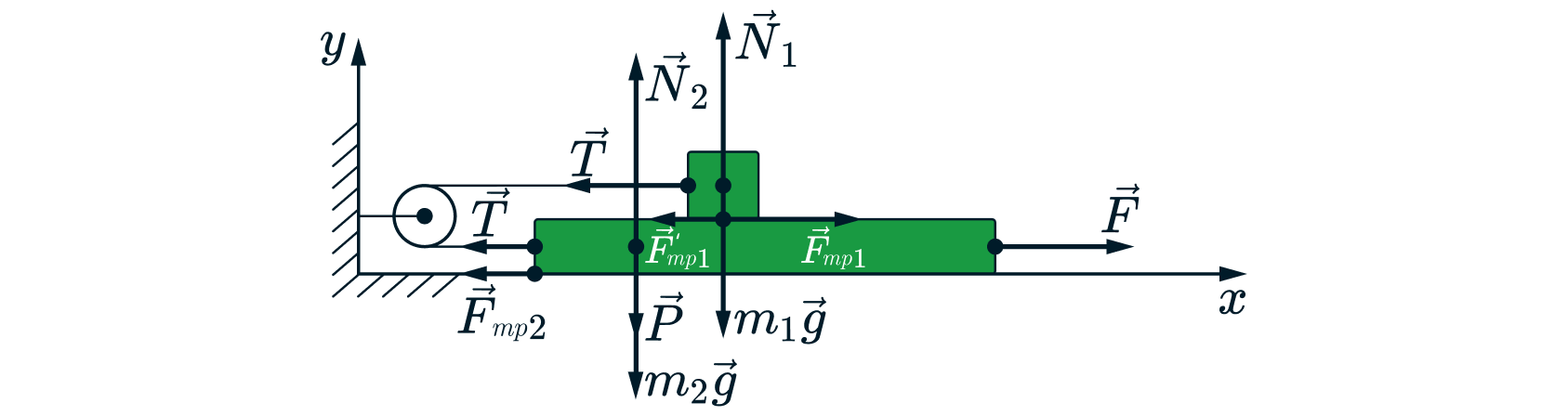
Здесь $T$ – сила натяжения нити, $N1$ – сила реакции опоры доски, $N2$ – сила реакции опоры стола, $Fтр1$ – сила трения между доской и бруском, $Fтр2$ – сила трения между столом и доской.
Ускорения доски и бруска равны, так как они связаны нерастяжимой нитью.
Запишем второй закон Ньютона для доски и бруска

⃗F + ⃗T + F⃗′ + F⃗тр2+ ⃗N2+ ⃗P + M⃗g = M ⃗a, тр1

T⃗+ F⃗ +N⃗ + m⃗g =m ⃗a. тр1 1

Здесь $a$ – ускорение, $P = N1,F′тр1 = Fтр1$ по 3 закону Ньютона.
Сила трения равна:

Fтр = μN. (1)

Спроецируем второй закон Ньютона на вертикальную ось:

N1 = mg

N2 = P + Mg = mg +Mg

Спроецируем второй закон Ньютона на горизонтальную ось, с учётом (1):

( { F − T − μ2(m + M )g − μ1mg = Ma ( T − μ mg = ma 1

Сложим два уравнения:

F − μ2(m + M )g− 2μ1mg = a(M + m) ⇒ F − μ2Mg − Ma = ma + μ2mg +2μ1mg

Отсюда выразим $m$ :

2 2 m = F-−-M-(μ2g-+a) = 6 Н-−-0,82-кг(0,3⋅120 м/-с-+1-м/с)-= 0,2 кг a+ g(μ2 +2μ1) 1 м/с + 10 м/с(0,3 + 2⋅0,5)

Ответ:

$F-−-M-(μ2g-+a) m = a+ g(μ2 +2μ1) = 0,2 кг$

Ошибка.
Попробуйте повторить позже

Задача 56#23085Максимум баллов за задание: 4

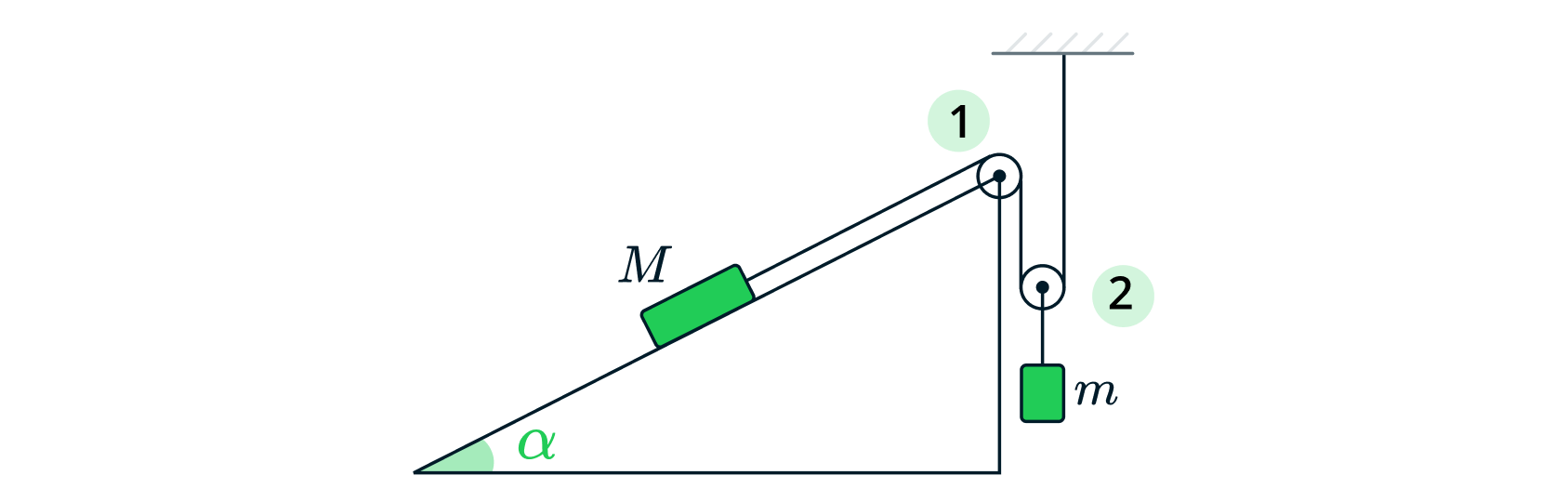
Брусок массой $M = 2$ кг располагается на неподвижной наклонной плоскости, образующей с горизонтом угол $∘ α = 30$ . К бруску привязана нить, перекинутая через два легких блока: неподвижный 1 и подвижный 2 (см. рис). Отрезки нити, идущие к подвижному блоку 2, вертикальны, а отрезок нити от бруска до неподвижного блока 1 параллелен наклонной плоскости. К оси подвижного блока подвешен груз, масса $m$ которого неизвестна. Когда систему предоставили самой себе, груз начал двигаться вниз с ускорением $a = 0,5$ м/с². Какова масса груза $m$ ? Коэффициент трения между бруском и наклонной плоскостью $μ = 0,2$ . Нить считайте невесомой и нерастяжимой, трением в оси блоков пренебрегите. Ускорение свободного падения примите равным $g = 10$ м/с². Какие законы Вы используете для решения задачи? Обоснуйте их применение.

ДВИ МГУ 2018

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками. Применим второй закон Ньютона, записывать его будем относительно ИСО.

3. Так как нить нерастяжима, то ее длина остается неизменной, значит можно использовать кинематические связи для описания движения тел.

4. Так как нить невесома и блоки идеальные, трение отсутствует, можно утверждать, что сила натяжения нити вдоль одной нити остается неизменной.

Решение

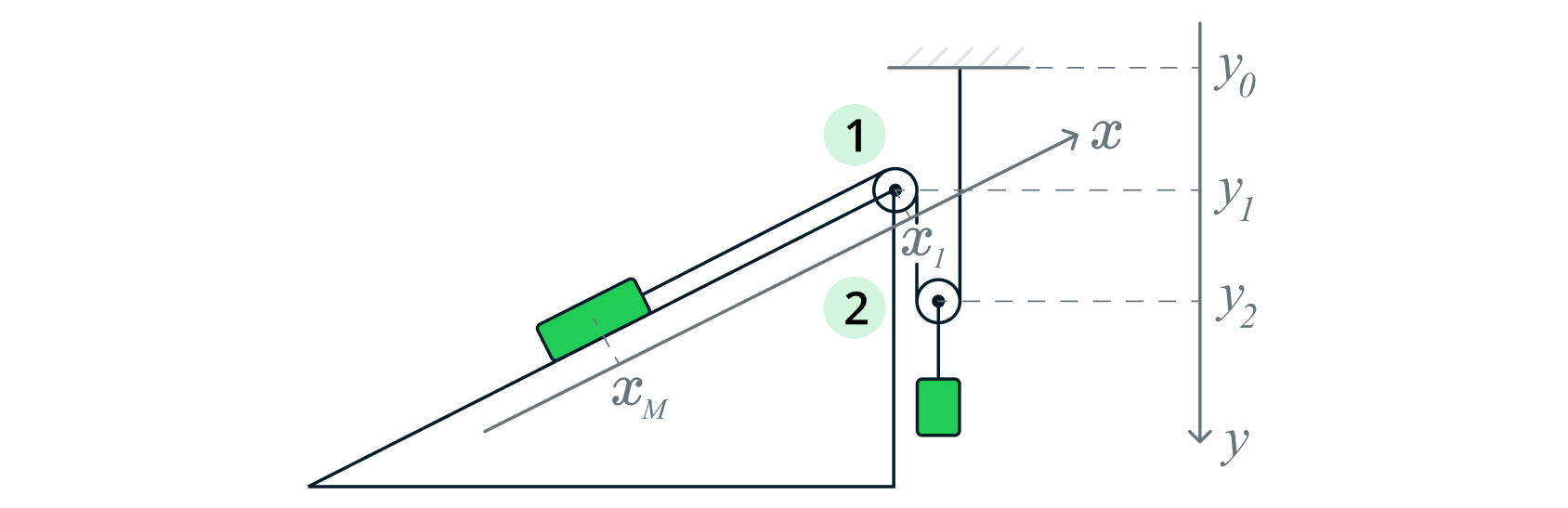
Длина нити равна:

(xM − x1)+ (y2− y1)+ (y2− y0) =l,

при этом $x1 = const$ , $y1 = const$ , $y0 = const$ , то в приращениях:

(ΔxM − Δx1) +(Δy2 − Δy1)+ (Δy2− Δy0) =Δl

И возьмём производную:

vMx+ 2v2y = 0,

возьмём вторую производную:

aMx+ 2a2y = 0,

где $aMx$ – проекция ускорения груза массой $M$ на Ох, $a2y$ – проекция ускорения груза массой $m$ на Оу.
Перейдем к записи через модули:

aM =2am,

где $aM$ – ускорение груза массой $M$ , $am$ – ускорение груза массой $m$ .
Расставим силы

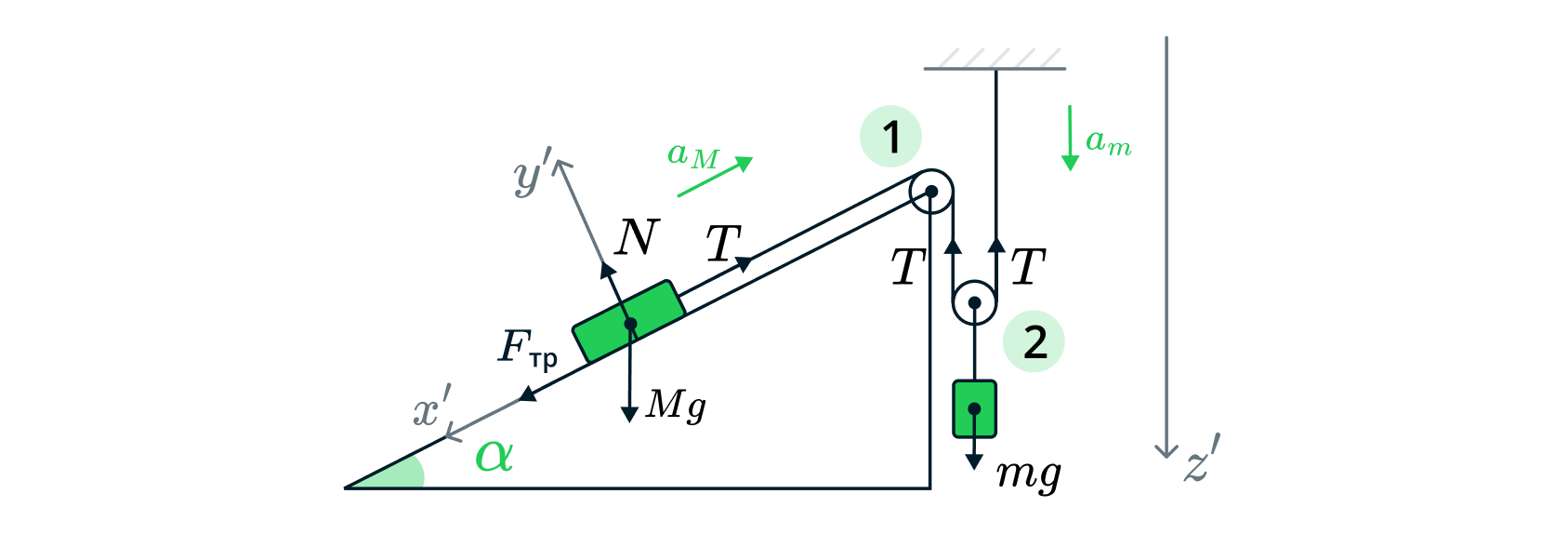
Запишем второй закон Ньютона для тел:

⃗Fтр +M ⃗g +N⃗+ ⃗T = M ⃗aM m⃗g +2⃗T = ma⃗m,

где $Mg$ и $mg$ – модули сил тяжести, $T$ – модуль силы натяжения нити, $N$ – модуль нормальной составляющей силы реакции опоры, $F тр$ – модуль силы трения скольжения ( $Fтр = μN$ ). Спроецируем второй закон Ньютона для тела $M$ на оси $x′$ и $y′$ и для тела $m$ на ось $z′$ :

(||x′ μN − T + Mg sinα = −MaM |{ ||y′ N = Mg cosα |(z′ mg − 2T = mam.

так как $aM = 2am$ , то

({ ′ x T − μMg cosα− Mg sinα = 2Mam (z′ mg − 2T =mam.

Сложим:

mg − 2μMg cosα − 2Mg sinα =ma + 4Ma

находим массу груза

2Mg (sin α+ μcosα)+ 4Ma m = ---------g−-a---------

√- 2 ⋅2 ⋅10 ⋅(0,5+ 0,2⋅-3-)+4 ⋅2⋅0,5 m = ------------------2-----------≈ 3,26 кг 10 − 0,5

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена ИСО.

2. Обоснована возможность использования в веденной системе отсчета второго закона Ньютона.

3. Сказано, что нить нерасятяжима, а значит можно использовать кинематические связи для описания движения тел.

4. Сказано, что тела можно рассматривать материальными точками.

5. Доказано, что сила натяжения нити не изменяется вдоль одной нити

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатные оси, скорость и ускорение записаны через производные от координаты и скорости по времени, получено уравнение кинематической связи).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 57#52213Максимум баллов за задание: 4

Систему из доски массой $m$ , бруска массой $5m$ и груза массой $3m$ удерживают в покое (см. рисунок). Затем систему отпускают, и доска движется по горизонтальной поверхности стола, а брусок движется по доске. Через время $t= 1,4$ с брусок достигает края доски, а доска ещё не доходит до блока. Коэффициент трения скольжения бруска о доску $μ1 = 0,1$ , а доски о стол $μ2 =0,3$ .
1) Определить ускорение бруска относительно стола при движении бруска по доске.
2) На каком расстоянии от края доски находился брусок до начала движения?
Массу нити, блока и трение в оси блока не учитывать.

Показать ответ и решение

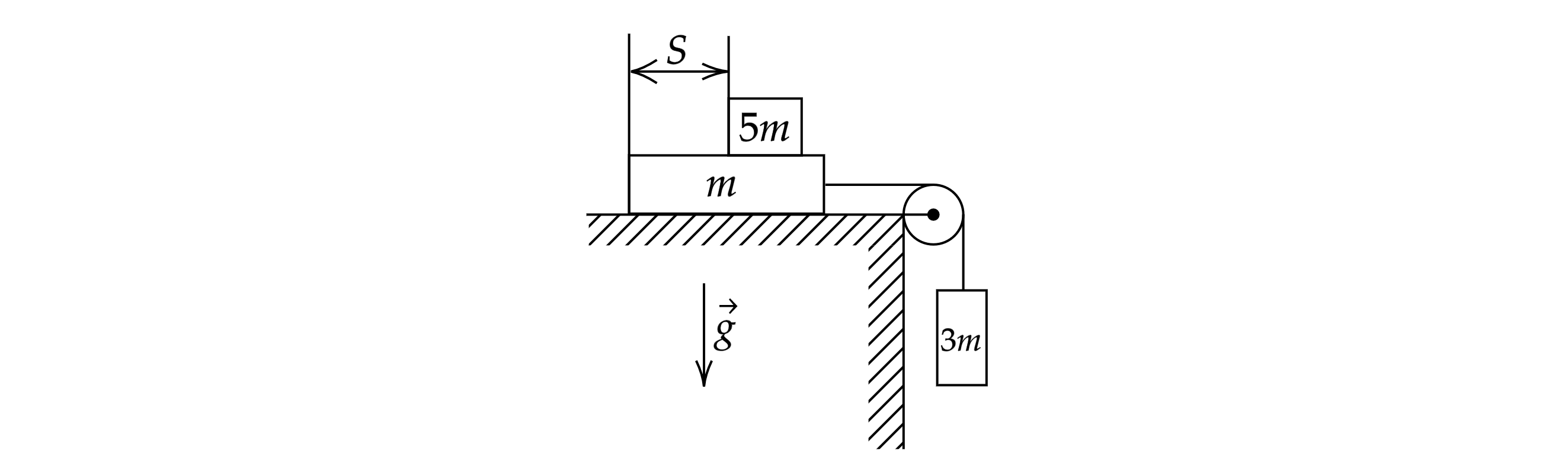
1) Расставим силы и введем оси, как показано на рисунке

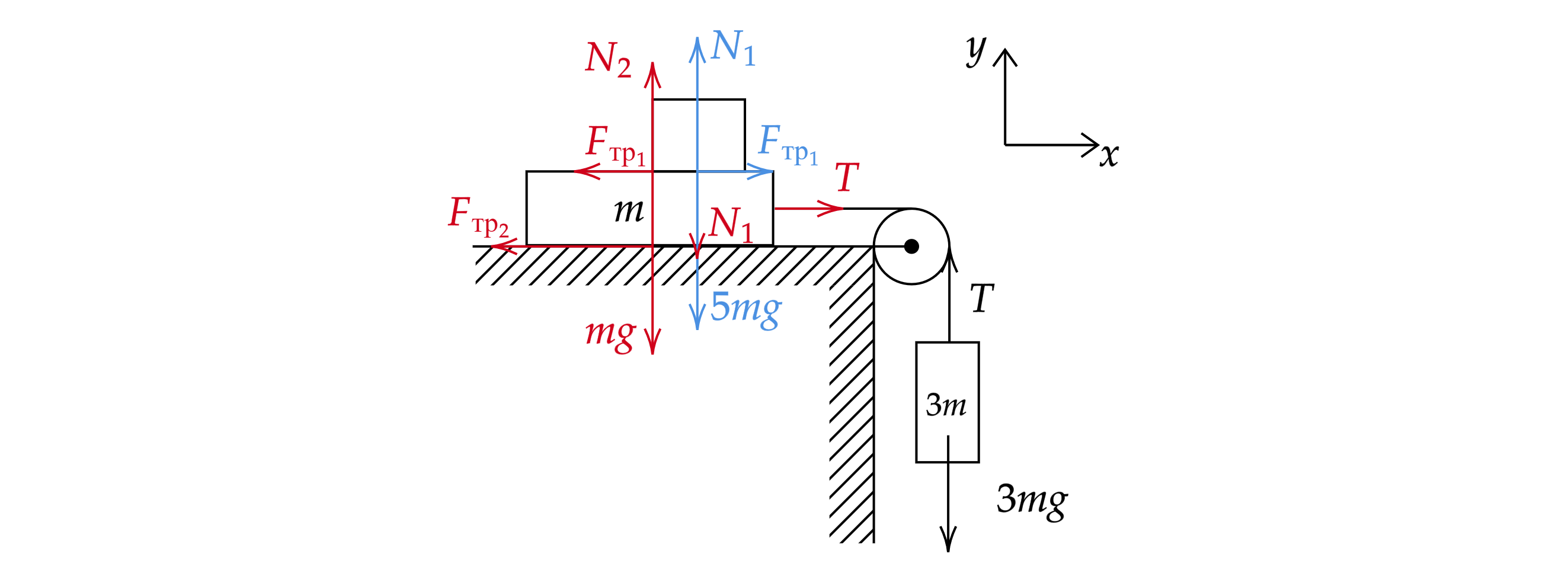
Где $N1$ – сила реакции опоры со стороны доски (давление бруска), $N2$ – сила реакции опоры со стороны стола, $Fтр1$ – сила трения между доской и бруском, $Fтр2$ – силе трения между доской и столом, $T$ – сила натяжения нити.
Красным обозначены силы, действующие на доску, синим – на брусок.
Запишем второй закон Ньютона для бруска:

⃗Fтр1 +N⃗1 + 5m⃗g = 5ma1,

где $a1$ – ускорение бруска.
Сила трения скольжения же равна:

Fтр1 =μ1N1,

где $μ1$ – коэффициент трения между бруском и доской.
Для нахождения силы трения скольжения спроецируем второй закон Ньютона для бруска на ось $y$ :

N1 = mg,

тогда сила трения

Fтр = μ15mg.

Спроецируем второй закон Ньютона для шайбы на ось $x$

F тр = ma1,

тогда

μ15mg = 5ma1 ⇒ a1 = μ1g = 0,1 ⋅10 м/с2 = 1 м/с2.

2) Запишем второй закон Ньютона для доски:

⃗Fтр1⃗Fтр2+ ⃗N1+ ⃗N2+ M ⃗g =ma2,

где $a2$ – ускорение доски.
И для груза

⃗T +3m ⃗g = 3m ⃗a3,

где $a3$ – ускорение груза.
Так как груз и доска связаны нерастяжимой, лёгкой нитью, то $a3 =a2$ . Спроецируем второй закон Ньютона для доски на ось $x$ :

−F тр1− Fтр2+T = Ma2

И на ось $y$ :

N2 − N1− mg = 0⇒ N2 = N1 +mg = 5mg + mg = 6mg.

Сила трения между доской и столом равна:

Fтр2 = μ2N2 = 6μ2mg,

где $μ2$ – коэффициент трения между доской и столом.
Тогда

T − 5μ1mg − 6μ2mg = ma2.

Спроецируем также второй закон Ньютона для груза на ось $y$ :

T − 3mg =− 3ma2.

Объединим последние два уравнения

g(3 − 5μ − 6μ ) 3mg − 5μ1mg − 6μ2mg = 4ma2 ⇒ a2 = ------14----2-.

Ускорение бруска относительно доски равно:

a= a2− a1 = g(3−-5μ1−-6μ2) − μ1g = 3g(1−-3μ1−-2μ2). 4 4

Искомое расстояние можно найти их уравнения кинематики:

2 S = v0t+ at-, 2

где $v0 = 0$ – начальная скорость бруска относительно доски.
Искомое расстояние равно:

at2 3g(1−-3μ1−-2μ2)t2- 3⋅10 м/с2(1-− 3-⋅0,1-− 2-⋅0,3)1,96-с2 S = 2 = 8 = 8 ≈ 0,75 м

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 58#52214Максимум баллов за задание: 4

Человек массой $m$ , упираясь ногами в ящик массой $M$ , подтягивает его с помощью каната, перекинутого через блок, по наклонной плоскости с углом наклона $α$ (см. рисунок). С какой минимальной силой надо тянуть канат человеку, чтобы подтянуть ящик к блоку? Коэффициент трения скольжения между ящиком и наклонной плоскостью равен $k$ . Части каната, не соприкасающиеся с блоком, параллельны наклонной плоскости. Массами блока и каната пренебречь
(МФТИ, 1998)

Показать ответ и решение

Расставим силы, действующие на ящик (красным) и человека (синим).

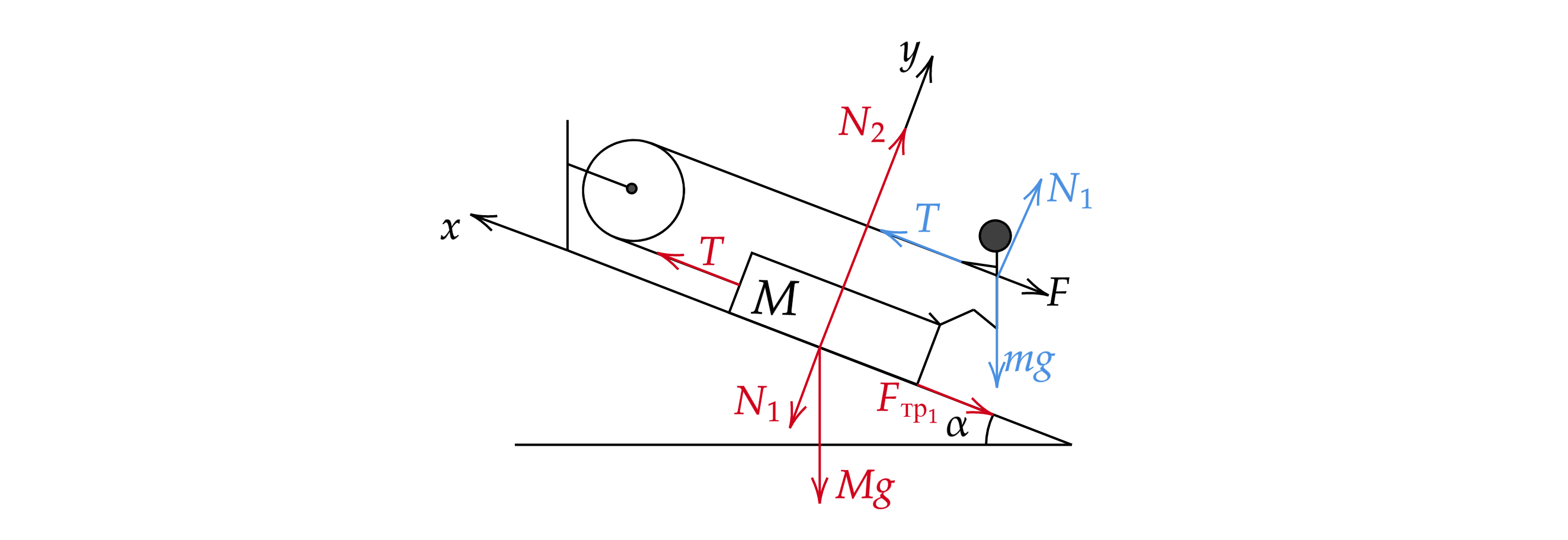
По третьему закону Ньютона $T = F$ . Данную систему можно заменить на аналогичную массой $M + m$ .

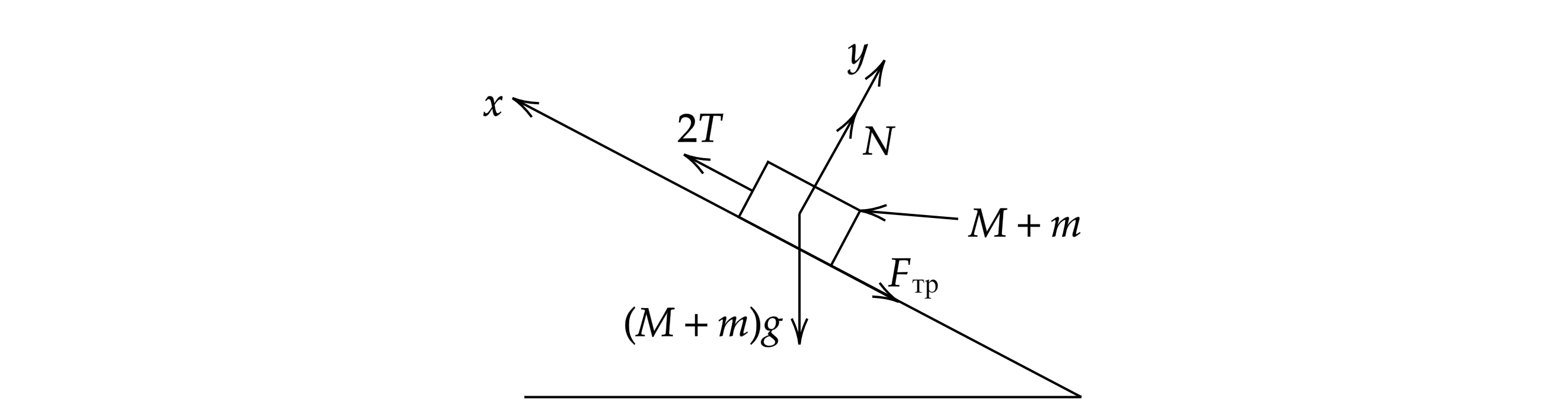
где $N$ – сила реакции опоры, $F тр$ – сила трения, $T$ – сила натяжения нити.
Запишем второй закон Ньютона:

F⃗тр+ ⃗N + (M + m)⃗g = (M + m)⃗a,

где $a$ – ускорение составного тела.
Спроецируем второй закон Ньютона на оси $x$ и $y$ :

( { x 2T − Fтр − (m + M )g sinα = (m + M )a ( y N − (m +M )gcosα =0.

Сила трения равна:

Fтр = kN.

Тогда

2F − k(m + M )gcosα − (m + M )g sinα =(m + M )a.

При этом сила $F$ минимальна, если $a= 0$ . Тогда

F = (m-+-M-)g(k-cosα-+sinα)- 2

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 59#47220Максимум баллов за задание: 4

На гранях закрепленной призмы находятся два груза массами $m1 = 2$ кг и $m2 =1$ кг, соединенные друг с другом и неподвижной опорой невесомыми и нерастяжимыми нитями через систему невесомых блоков (см. рис.). Правая грань призмы гладкая, левая – шероховатая с коэффициентом трения $μ= 0,6$ . Определите модуль ускорения левого груза $a1$ . Углы при основании призмы $α = 60∘$ , $β = 30∘$ . Ускорение свободного падения примите равным $g = 10$ м/с $2.$
ДВИ МГУ 2018

Показать ответ и решение

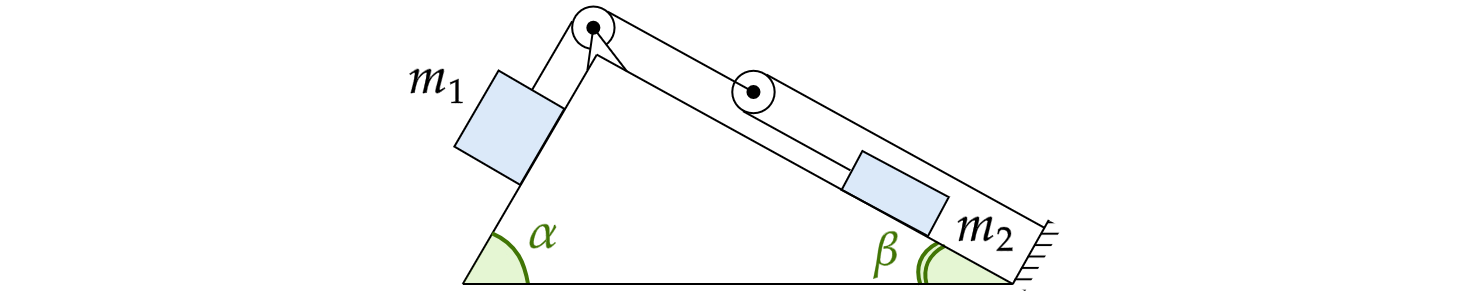
Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Все тела движутся поступательно, поэтому их можно считать материальными точками.

3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.

4. Так как нити невесомые, блок идеален, то модуль силы натяжения нити в любой её точке один и тот же.

5. Нить нерастяжима, поэтому модули ускорений блоков при их прямолинейном поступательном движении отличаются в два раза.

Решение

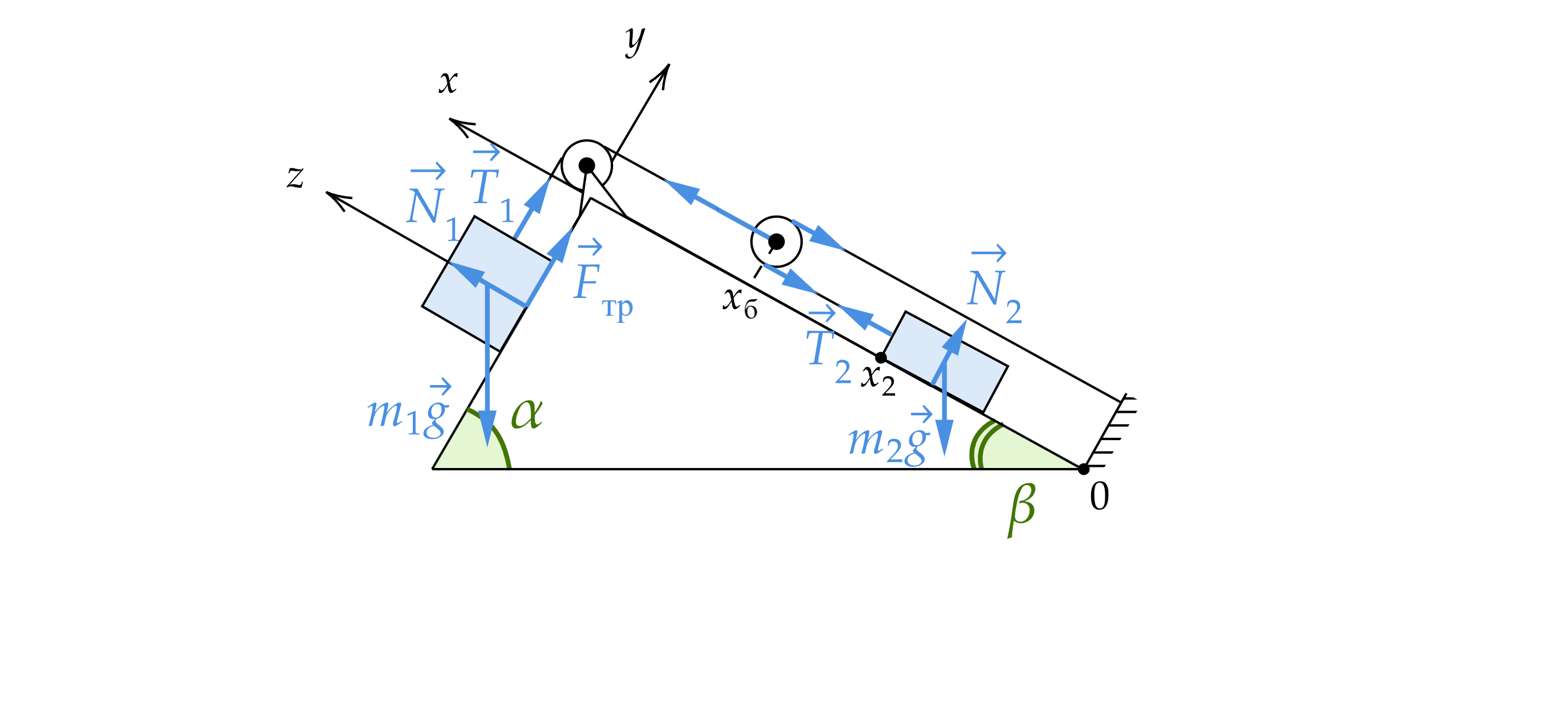
Тела движутся под действием сил, изображенных на рисунке, где $m1,2⃗g$ - силы тяжести, $N⃗1,2$ - нормальные составляющие сил реакции призмы, $T⃗1,2$ - силы натяжения нитей, $F⃗тр$ – сила трения скольжения. По второму закону Ньютона имеем:

m1 ⃗g+ ⃗T1+ F⃗тр = m1⃗a1.

Спроецируем на оси $y$ и $z$ :

( {m1g sinα − T1− Fтр = m1a1 ( N1 = m1g cosα.

Сила трения же равна:

F тр = μN1,

тогда можно записать уравнение

m1gsinα− T1− μm1g cosα = m1a1

аналогично для правого

m2⃗g+ ⃗T2 =m2 ⃗a2,

спроецируем на ось $x$ :

T2− m2gsinβ = m2a2.

Ускорение блока равно ускорению груза 1. Найдём длину нити, привязанную к грузу 2:

(xб− x2)+ (xб − 0)= l,

в приращениях

Δ (xб − x2)+ Δ(xб− 0)= Δl,

разделим на $Δt$ и получим производную

x′б− x′2+x′б − 0′ = l′ ⇒ vбх − v2x+ vбх = 0.

Аналогично получим связь ускорения блока и груза 2:

2aбх= a2x.

С учётом проекции на ось, получаем связь модулей ускорений $a2 =2a$ . Так как ускорение блока и груза 1 равны (нити нерастяжимы и невесомы), то $a2 = 2a1$ . Кроме того $T1 = 2T2$ . Тогда можно составить систему уравнений:

( { m1gsin α− T1− μm1g cosα = m1a1 (m1sinα− 2m2 sinβ − μm1 cosα) ( ⇒ a= ---------m1-+-4m2----------g 2T1− m2gsin β = 2m2a1

Подставляем числа из условия

(2 кг ⋅sin60∘− 2⋅1 кг⋅sin30∘− 0,6⋅2 кг⋅cos60∘) a= ---------------2-кг+-4⋅1 кг--------------10 м/с2 ≈ 0,22 м/с2

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета

2. Обоснована возможность применения к телам модели материальной точки

3. Обосновано применение второго закона Ньютона для описания движения тел

4. Обосновано равенство сил натяжения нитей

5. Расписана связь между ускорениями тел

______________________________________________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

________________________________________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на выбранные координатные оси, уравнения кинематической связи для координат тел, их скоростей и ускорений, формула силы трения скольжения).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

________________________________________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

________________________________________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Ошибка.
Попробуйте повторить позже

Задача 60#19210Максимум баллов за задание: 4

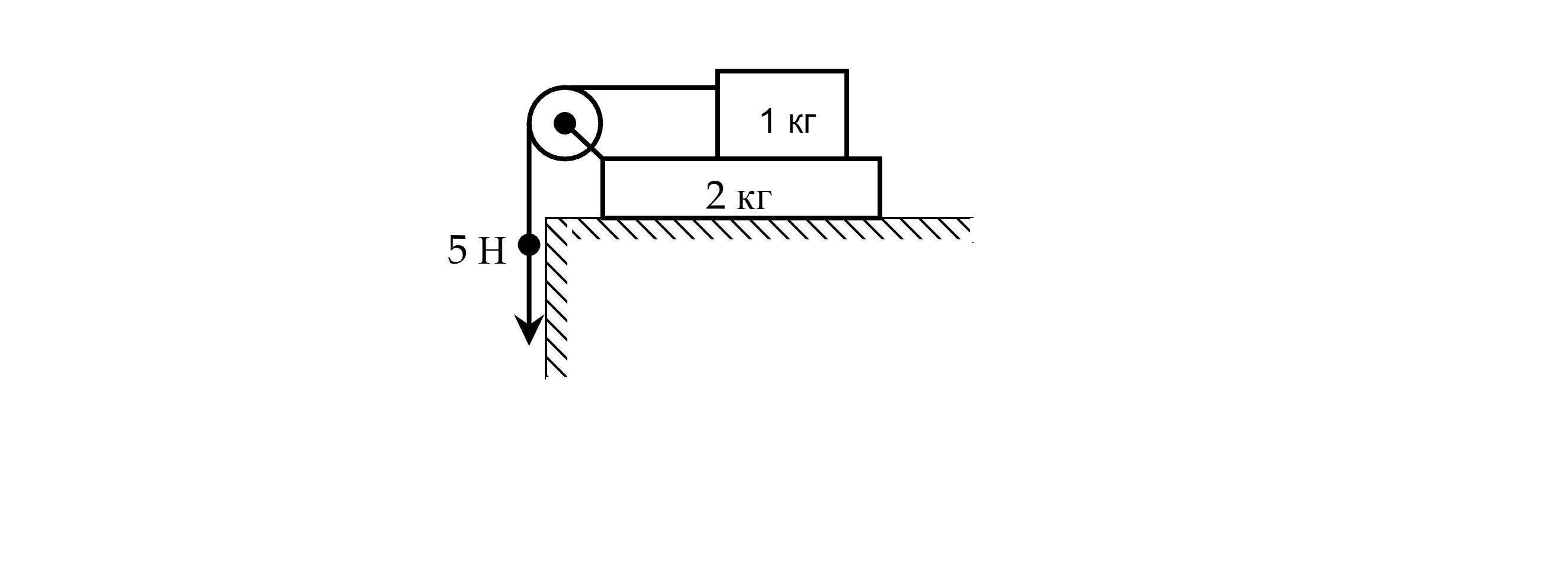
На столе лежит доска массой $m1 =2$ кг, а на доске находится брусок массой $m2 = 1$ кг. К бруску привязана лёгкая нить, второй конец которой перекинут через идеальный блок, закреплённый на краю доски. Коэффициенты трения между доской и столом и между бруском и доской одинаковы и равны $μ = 0,1$ . Участок нити между бруском и блоком горизонтален. С какими по модулю ускорениями начнут двигаться брусок и доска, если к вертикальному участку нити приложить направленную вниз силу $F = 5$ Н? Ускорение свободного падения можно считать равным $g =10 м/с2$ . Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Тела движутся поступательно, поэтму будем считать их материальными точками

3. Так как тела являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.

Решение

Сделаем рисунок с изображением сил.

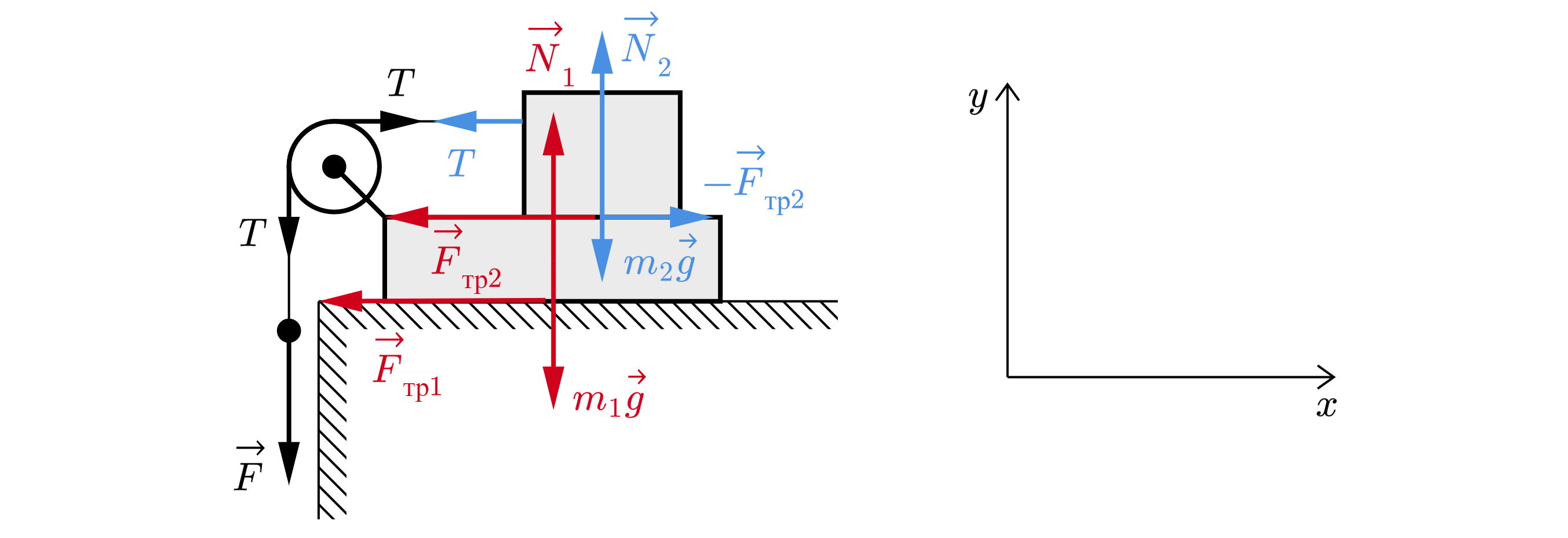
Из второго закона Ньютона $T = F$ .
Запишем второй закон Ньютона для доски и для бруска:

√ - ⃗T 2+ F⃗тр1 +F⃗тр2+ ⃗N1+ m1⃗g+ ⃗N2 = m1 ⃗a1.

⃗T + ⃗N2+ m2⃗g +F⃗тр2 = m2a⃗2.

Спроецирем второй закон Ньютона на оси $x$ и $y$ :

( {T − Fтр1− Fтр2 = m1a1 ( N1 − N2− m1g − F = 0

({ T − F тр2 = m2a2 ( N2 − m2g = 0

При этом силы трения равны:

F =μN F = μN . тр1 1 тр2 2

При этом из системы уравнений:

N = m g N =N + m g = (m + m )g 2 2 1 2 1 1 2

F = μ((m + m )g+ F) F = μm g. тр1 1 2 тр2 2

Тогда

F − μ(m1+ m2)g+ F + μm2g F − μm2g a1 =-----------m1----------- = 0,25 м/с2 a2 =---m2--- = 4 м/с2

Ответ:

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета

2. Обоснована возможность применения к телам модели материальной точки

3. Обосновано применение законов Ньютона для описания движения тел

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме и в проекции на координатную ось, формула силы трения скольжения, третий закон Ньютона).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в формулах.)

И (ИЛИ)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

И (ИЛИ)

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.