Регион 9 класс
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На прямой дороге стоят школа и дома Ани и Бори. Каждый день Аня выходит из дома в и идет в школу. Однажды Боря выбежал из
дома в школу в
и догнал Аню за 30 минут. На следующий день он выбежал в
и догнал Аню за 40 минут. В какое время
ему надо выбежать, чтобы встретить Аню на выходе из её дома? (Скорость Ани всегда постоянна, скорость Бори тоже
постоянна.)
Источники:
Подсказка 1:
Это обычная задача на движение. Давайте обозначим через S расстояние между домами, а через x и y - скорости Ани и Бори. Интерпретируйте информацию из условия с помощью этих переменных.
Подсказка 2:
Чтобы понять, во сколько Боре нужно выйти, нужно найти величину S/y. Именно столько времени ему идти до дома Ани.
Подсказка 3:
Скорее всего вы получили два равенства S = 30(y − x) = 40(y − x) − 10x. Попробуйте с их помощью выразить две переменные через третью.
Первое решение. Пусть — расстояни между домами Ани и Бори (измеренное в метрах), а
и
— скорости Ани и Бори
соответственно (измеренные в м/мин). Когда Боря догоняет Аню, скорость их сближения равна
Поэтому в первый день Боря
догнал Аню за
мин. Во второй же день Аня успела отойти на
м, так что
мин. Отсюда имеем
откуда
и
Поэтому
а Боре надо потратить на путь между домами
минут. Значит, выбежать ему надо в
______________________________________________________________________________________________________________________________________________________
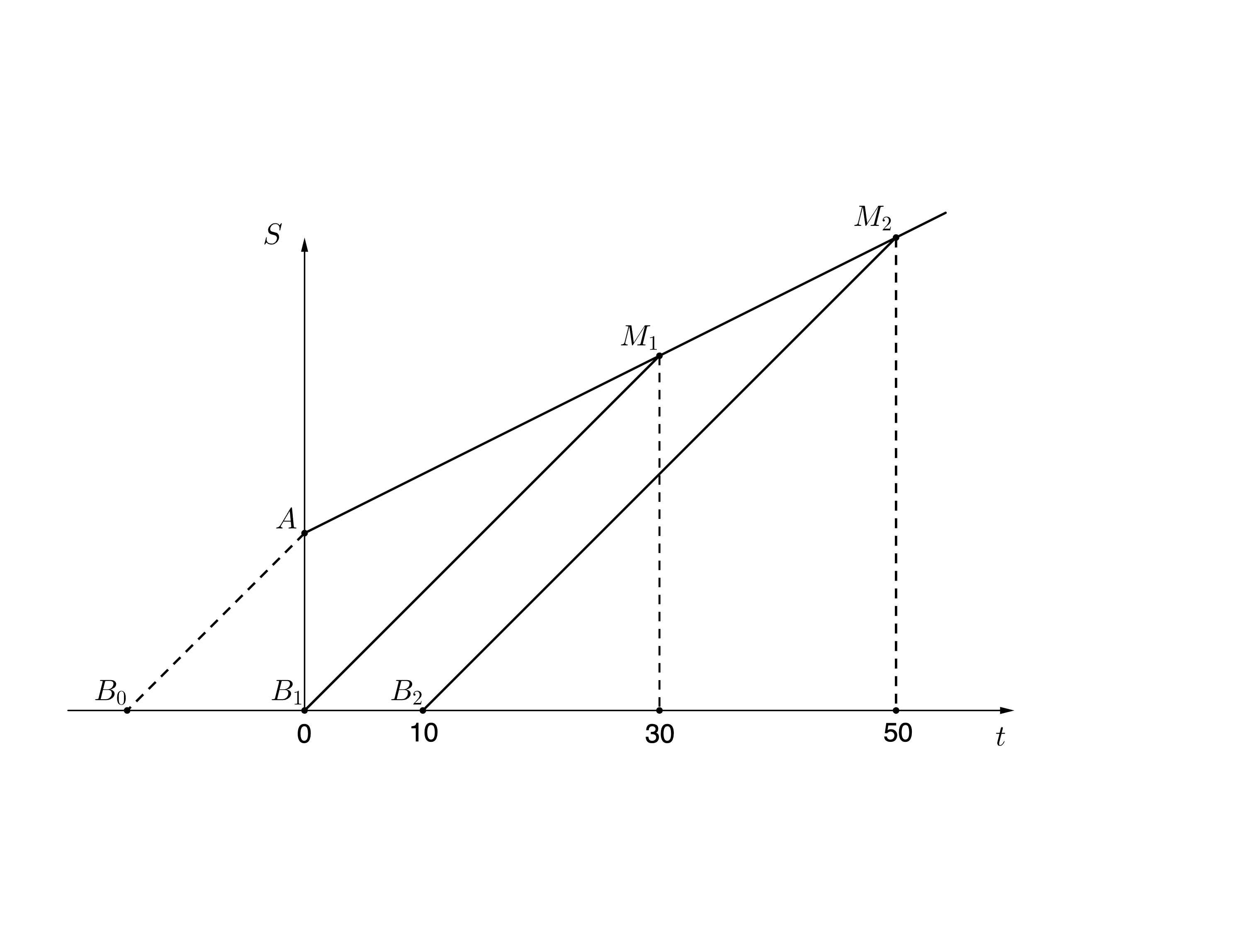
Второе решение. Изобразим условие на графике (см. рис. 1), откладывая по оси абсцисс время (в минутах, отсчитанное от момента
), а по оси ординат — расстояние от дома Бори. Тогда графики движения обоих детей будут отрезками прямых. Пусть график
движения Ани начинается в точке
график движения Бори в первый и второй день — в точках
и
и пусть точки
встречи в эти два дня обозначаются как
и
соответственно. По условию, абсциссы точек
и
равны 30 и 50
соответственно.
Пусть — точка, в которой должен начинаться график движения Бори. По теореме Фалеса,
последнее отношение
равно отношению разностей абсцесс соответствующих точек, то есть
Значит,
то есть точка
соответствует моменту
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике (
) проведена биссектриса
На основании
отмечена точка
так,
что
Точка
выбрана таким образом, что четырёхугольник
—– параллелограмм. Докажите, что
Источники:
Подсказка 1:
У вас должно возникнуть желание продлить ED до пересечения с AC в точке X. Почему? Во-первых, эта прямая будет отсекать равнобдренный треугольник от ABC. Во-вторых, имеется биссектриса DC и можно будет удачно перекинуть углы. Поработайте с этой картинкой.
Подсказка 2:
Скорее всего, у вас возникает желание доказать через счёт углов, что треугольник EBF равнобедренный. Попробуйте пойти другим путём. Найдите какую-нибудь пару равных треугольников, в которых отрезки BE и BF являются соответствующими сторонами.
Подсказка 3:
Обратите внимание на треугольники BXE и FCB.
Первое решение. Продолжим отрезок до пересечения со стороной
в точке
Поскольку
треугольник
равнобедренный. Кроме того,
поэтому треугольник также равнобедренный, и
Из параллелограмма
получаем
Тогда
Поскольку получаем, что треугольники
и
равны по двум сторонам и углу между ними, откуда и
следует, что
![]()
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Пусть описанная окружность треугольника пересекает вторично прямую
в точке
Тогда
также, поскольку —– (внутренняя или внешняя) биссектриса угла
имеем
Поэтому треугольники и
равны. Отсюда следует, что
а тогда и треугольники и
также равны. Значит,
Кроме того, из полученного равенства углов
и
следует, что
Тогда треугольники и
также равны, и
что и требовалось.
![]()
Ошибка.
Попробуйте повторить позже
Даны квадратные трёхчлены и
обозначим
и
Раз в минуту Саша рисует на координатной плоскости
прямую: на первой минуте — прямую с уравнением
на второй — с уравнением
…, на
-й минуте — с уравнением
Через некоторое время Саша нашёл три нарисованные прямые, которые проходят через одну точку. Докажите, что все
нарисованные прямые проходят через одну точку.
Источники:
Подсказка 1:
Давайте возьмём какие-то две прямые, проведенный на k-й и m-й минутах, которые пересеклись. Что можно сказать про абсциссу точки пересечения? Получится ли как-нибудь выразить её через k, m и коэффициенты трёхчленов?
Подсказка 2:
Пусть теперь есть три прямые: k-я, m₁ и m₂. Значит, эту абсциссу можно выразить как через m₁, так и через m₂. Попробуйте приравнять их.
Подсказка 3:
Если вы сделали всё правильно, то должны были получить равенство (k + m₁)(ub − av)=(k + m₂)(ub − av), где a, b — коэффициенты при второй и первой степенях соотвественно у P, и u, v — у Q.
В каких случаях это равенство возможно при m₁ ≠ m₂? Задаёт ли это равенство какие-то ограничения на m₁ и m₂?
Пусть а
Пусть прямые, нарисованные на -й и
-й минутах, пересекаются в точке с абсциссой
(причём
). Это значит, что
или
если
Пусть теперь прямые, нарисованные на -й,
-й и
-й минутах пересекаются в одной точке. Заметим, что квадратный
трёхчлен
принимает каждое значение не более двух раз, поэтому в множестве
есть хотя бы два
раличных значения. Без ограничений общности будет считать, что
Тогда полученная формула означает,
что
Домножив на знаменатели и сократив подобные слагаемые, получаем
что при означает, что
Таким образом, равенство выше верно вообще для всех значений
и
а значит, и
равенство (**) будет выполнено для всевозможных значений
и
что и означает, что прямые, нарисованные в произвольные
моменты
и
пересекают
-ю прямую в одной и той же точке.
Рассуждение выше может не сработать только для момента когда
Но, поскольку нам уже известно, что все остальные
прямые пересекаются в одной точке, можно теперь провести такое же рассуждение для других трёх моментов, установив
требуемое.
Ошибка.
Попробуйте повторить позже
В каждой клетке доски лежит по рублёвой монете. Даша и Соня играют, делая ходы по очереди, начинает Даша. За один ход
можно выбрать любую монету и передвинуть её: Даша двигает монету на соседнюю по диагонали клетку, Соня — на соседнюю по стороне.
Если две монеты оказываются в одной клетке, одна из них тут же снимается с доски и достаётся Соне. Соня может остановить игру
в любой момент и забрать все полученные деньги. Какой наибольший выигрыш она может получить, как бы ни играла
Даша?
Источники:
Подсказка 1:
Чтобы придумать стратегию за Соню, попробуйте разбить доску на какие-нибудь маленькие части, в рамках которых она сможет легко получать монеты.
Подсказка 2:
Разбейте на квадраты 2 на 2. Давайте заметим, что если в таком квадрате есть хотя бы 2 монеты, то Соня легко сможет получить одну из них (почему?). Исходя из этого, можно понять, каким будет ответ.
Подсказка 3:
Итак, скорее всего вы поняли, что ответ будет 300. Осталось придумать стратегию за Дашу, с помощью которой она всегда сможет сохранить 100 монет на доске. Попробуйте выбрать 100 монет, находящихся в каких-то определённых столбцах.
Подсказка 4:
Будет здорово, если эти столбцы не будут рядом. Тогда Соне будет сложнее забрать какую-то из выбранных монет. Значит, можно взять, например, нечётные столбцы и придумать стратегию, при которой после каждого хода Даши выбранные монеты находятся в этих столбцах.
Сначала приведём стратегию за Соню. Пока она не получила больше 299 монет, перед её ходом на доске остаётся хотя бы 101 монета.
Разобьем доску на 100 квадратов Получается, что какие-то две монеты лежат в одном и том же квадрате
Если эти две
монеты соседние по стороне, то Соня надвигает одну на другую, и получает ещё одну монету. Если они стоят по диагонали, то Соня сдвигает
одну из них в столбец к другой (здесь и далее столбец имеет длину 2, строка — длину 200). Теперь, какой бы ход ни сделала Даша, эти две
монетки всё ещё будут соседними по стороне (либо одна будет снята и уйдёт в доход Сони), значит, своим следующим ходом Соня
сможет получить ещё одну монетку. Таким образом, Соня всегда сможет увеличивать свой выигрыш, пока он меньше
300.
Теперь покажем, как играть за Дашу, чтобы Соня не получила больше 300 монет. Пронумеруем столбцы числами от 1 до 200 по порядку, выберем в каждом нечётном столбце по одной монетке и мысленно покрасим их в красный цвет. Даше достаточно обеспечить, чтобы красные монетки всегда оставались на доске. Для этого, в свою очередь, достаточно, чтобы две красные монеты никогда не попадали в одну клетку, потому что когда в клетку попадают красная и не красная монеты, можно считать, что с доски снимается не красная.
Назовём расположение монет на доске стабильным, если по одной красной монете лежит в столбцах а
ещё одна располагается в одном из двух последних столбцов 199, 200. Легко видеть, что после любого хода из стабильной
позиции две красные монеты не окажутся в одной клетке. Даша будет играть так, чтобы после каждого её хода получалась
стабильная позиция. Если после хода Сони позиция осталась стабильной, то Даша двигает сотую красную фишку между двумя
последними столбцами, так же Даша поступит и своим первым ходом. Если же после хода Сони позиция перестала быть
стабильной, то Соня подвинула одну из красных монет из некоторого столбца
в соседний столбец. Тогда Даша своим ходом
вернёт её в столбец
Таким образом, на доске всегда останется хотя бы 100 монет, и Соня заработает не более трёхсот
рублей.
300
Ошибка.
Попробуйте повторить позже
Найдите все такие пары целых чисел и
, что
Источники:
Подсказка 1:
Давай заметим, что в правой части равенства почти полный квадрат. Не хватает 1. Давайте добавим её слева и справа.
Подсказка 2:
Также хотелось бы разложить на скобочки левую часть, притом желательно на взаимно простые. Если не получается угадать разложение, рассмотрите выражение слева как квадратный трёхчлен относительно (n-2)!.
Подсказка 3:
Итак, вы получили равенство ((n - 1)! - 1)((n - 2)! - 1) = (m - 1)². Являются ли скобки в левой части взаимно простыми?
Подсказка 4:
Для дальнейших продвижения необходимо вспомнить, что если произведение взаимно простых чисел равно квадрату, то каждое из них является квадратом. Кстати, почему это так?
Подсказка 5:
Теперь осталось показать, что при больших n какая-то из скобок не сможет быть большим квадратом. Учитывая особенности факториалов, стоит подумать про остатки. Например, при делении на 4 квадраты могут иметь далеко не все остатки.
Заметим, что
Пусть Заметим, что числа
и
взаимно просты. Предположим, что это не так, и оба этих числа делятся
на простое число
Тогда число
тоже делится на Тогда
делится на
а
не кратно
противоречие. Таким образом, произведение взаимно
простых чисел
и
—– точный квадрат, тогда и каждое из них точный квадрат. Однако, число
при
даёт остаток 3 при делении на 4, поэтому оно точным квадратом быть не может. Остаётся разобрать случаи
При
получается
решений нет. При
мы получаем:
что даёт единственное решение
,
Ошибка.
Попробуйте повторить позже
Пусть на доске написаны несколько целых чисел (некоторые из которых могут быть равными). Скажем, что эти числа образуют удачный набор, если их нельзя разбить на две непустые группы так, чтобы произведение суммы чисел в одной группе и суммы чисел в другой было положительным. Учитель написал на доске несколько целых чисел. Докажите, что дети могут дописать к имеющимся ещё ровно одно целое число так, чтобы полученный набор оказался удачным.
Источники:
Подсказка 1:
Иными словами, от нас хотят, чтобы при любом разбиении набора на 2 группы знаки сумм чисел в группах были разными. Какой должна быть сумма чисел в наборе, чтобы сразу стало очевидно, что он удачный?
Подсказка 2:
Разумеется, нулём (кстати, почему в этом случае очевидно, что набор удачный?). А какое число нужно дописать для произвольного удачного набора, чтобы сумма чисел в нём стала 0?
Пусть сумма всех чисел, выписанных учителем, равна тогда детям достаточно дописать число
Действительно, после этого сумма
всех чисел окажется равной нулю, а значит, при разбиении их на две группы суммы в группах будут противоположными друг другу, то есть
их произведение будет неположительным.
Ошибка.
Попробуйте повторить позже
На столе по кругу выложили 100 двухрублёвых и пятирублёвых монет в некотором порядке. Известно, что выбрав из круга несколько
подряд идущих монет, невозможно получить сумму ровно в 52 рубля. Найдите наибольшее возможное значение числа
Источники:
Подсказка 1:
Проще начать с оценки и делать её стоит следующим образом. Давайте пронумеруем 100 двухрублевых монет в порядке их расположения по кругу. Как должны быть расположены пятирублевые монеты, чтобы набралась нужная сумма?
Подсказка 2:
Если вокруг какой-то из двухрублевых монет будет суммарно хотя бы 10 пятирублевых, то сумма 52 наберётся. Подумайте, как сделать оценку, используя это.
Подсказка 3:
Разумно будет рассмотреть двухрублевые монеты с нечетными номерами. В каждом из 10 промежутков между выделенными монетами не должно быть более 9 монет. Отсюда можно получить оценку.
Подсказка 4:
Итак, вы получили оценку на 450. Осталось придумать пример с 450 монетами. Разумным ходом будет сделать так, чтобы между каждой двухрублевой монетой было либо 4, либо 5 пятирублевых монет, тогда условие из подсказки 2 не будет выполняться.
Покажем, как выложить 100 двухрублёвых и 450 пятирублёвых монет по кругу так, чтобы выполнялось условие задачи. Пронумеруем места по кругу по часовой стрелке числами от 1 до 550 и выложим двухрублёвые монеты на места, номера которых кратны 11 (т. е. 11, 22, …), и на места, номера которых дают остаток 5 при делении на 11 (т. е. 5, 16, …); на остальные места выложим пятирублёвые монеты. Тогда между каждой парой соседних двухрублёвых монет находятся 4 или 5 пятирублёвых монет, причём эти количества чередуются.
Рассмотрим некоторый набор подряд идущих монет; покажем, что они не дают сумму в 52 рубля. Если среди них нет двухрублёвых, то
сумма делится на 5, а 52 не делится на 5. Если среди них ровно две двухрублёвых, сумма даёт остаток 4 при делении на 5, то есть тоже не
равна 52. Если двухрублёвая монета одна, вместе с ней в наборе может быть не более пятирублёвых, то есть сумма не
превосходит
рублей. Наконец, пусть двухрублёвых монет в наборе хотя бы три, рассмотрим три двухрублёвых монеты,
лежащих в наборе подряд. Между ними есть 9 пятирублёвых; суммарное достоинство этих монет уже равно
рублю. Значит,
набрана сумма либо в 51 рубль, либо хотя бы в
рубля. Таким образом, полученная раскладка удовлетворяет
условию.
Осталось показать, что при любой раскладке 100 двухрублёвых и не менее 451 пятирублёвых монет обязательно можно выбрать
несколько монет подряд с суммарным достоинством 52 рубля. Пронумеруем двухрублёвые монеты числами 1, 2, …, 100 в порядке их
расположения по часовой стрелке. Выделим 50 двухрублёвых монет с нечётными номерами. Между выделенными монетами есть 50
промежутков; в одном из них окажется не менее 10 пятирублёвых монет, иначе общее количество пятирублёвых монет не
превосходило бы Итак, мы нашли промежуток, в котором есть ровно одна двухрублёвая монета
и хотя бы 10
пятирублёвых; тогда можно взять
и 10 пятирублёвых монет так, чтобы они лежали подряд. Тогда и наберётся сумма ровно в 52
рубля.
Ошибка.
Попробуйте повторить позже
На столе стоят 12 сосудов, выстроенных в 4 ряда по 3 сосуда в каждом. В каждый сосуд налито некоторое (возможно, нулевое) количество
воды. Известно, что суммарное количество воды в каждом ряду равно 1 л. При каких можно утверждать, что на столе найдутся два
сосуда, количества воды в которых отличаются не более чем на
л?
Источники:
Подсказка 1:
Нужно получить какую-то оценку на α, учитывая, что в каждом ряду суммарно 1 литр воды. Попробуйте предположить, что количество воды в любых двух сосудах отличается больше, чем на α. Оцените α при таких условиях.
Подсказка 2:
Хорошей идеей будет упорядочить сосуды по возрастанию количества воды в них. Ясно, что если сосуд стоит на i-м месте в упорядоченном ряду, в нём более i • α воды. Как связать это с тем, что в каждом ряду суммарно 1 литр воды?
Подсказка 3:
С помощью принципа Дирихле можно найти максимальное число M, для которого всегда найдется ряд, сумма индексов которого не меньше M. Это даст оценку на α. Также не забудьте придумать пример, показывающий, что меньшие α не подойдут.
Предположим, что количество воды в любых двух сосудах отличается больше, чем на л. Пусть
— количества воды в
сосудах; назовём индексом сосуда его номер в этом ряду. Заметим, что
и по нашему предположению
отсюда
получается, что
при
Сумма всех индексов равна
поэтому найдётся ряд, сумма индексов в котором не меньше, чем 17. Из неравенств выше получаем, что суммарное
количество воды в этом ряду больше, чем откуда
Итак, при всех значениях
утверждать требуемое
можно.
С другой стороны, если распределить воду по рядам как
то количества воды в любых двух сосудах будут отличаться минимум на л. Поэтому при всех
утверждать требуемое
нельзя.
При
Ошибка.
Попробуйте повторить позже
Пусть — середина стороны
треугольника
На продолжении стороны
за точку
нашлась такая точка
что
Точка
— центр окружности, описанной около треугольника
Найдите угол
Источники:
Подсказка 1:
Чтобы решить задачу, нужно что-то понять про BO. Например, было бы неплохо найти какую-нибудь вспомогательную конструкцию, которая даст больше информации про BO.
Подсказка 2:
Можно попробовать угадать такую конструкцию. Что если рассмотреть такую точку P, что треугольник BPC — равносторонний, и точки A и B лежат по разные стороны от BC?
Подсказка 3:
Обратите внимание на четырёхугольники BDPM и ADPC. Они вписанные, не так ли? Отсюда уже нетрудно получить ответ.
Отметим точку так, что треугольник
— равносторонний, а точки
и
лежат по разные стороны от прямой
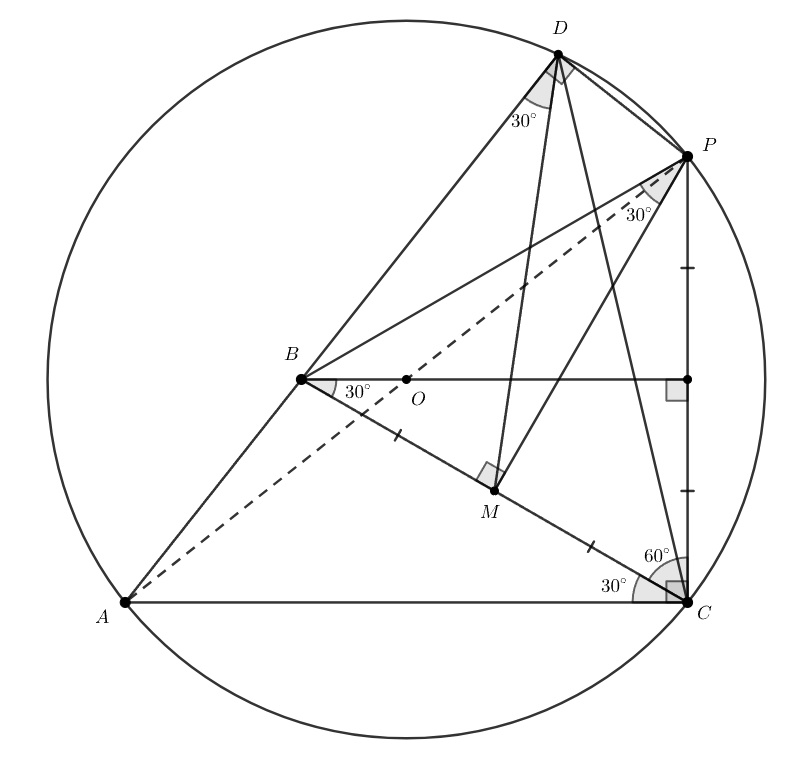
Тогда
то есть четырёхугольник — вписанный; значит, поскольку
то и
Но, так как
четырёхугольник также вписан в окружность (с диаметром
), и точка
из условия — центр этой окружности. В
частности,
лежит на серединном перпендикуляре к
совпадающем с биссектрисой угла
Отсюда и вытекает, что
Ошибка.
Попробуйте повторить позже
У Олега есть набор из 2024 различных клетчатых прямоугольников размеров
…,
(по одному прямоугольнику
каждого размера). Может ли он, выбрав некоторые из них, составить какой-нибудь клетчатый квадрат площадью больше
1?
Источники:
Подсказка 1:
Предположим, что это возможно. Пусть n — наибольшая из длин выбранных прямоугольников. Попробуйте как-нибудь оценить площадь квадрата.
Подсказка 2:
Например, ясно, что его площадь не меньше n², поскольку сторона не меньше n. Возможно, можно найти какое-то противоречие с этим?
Подсказка 3:
Какой может быть наибольшая площадь выбранных прямоугольников?
Предположим противное, и пусть — наибольшая из длин выбранных прямоугольников. Тогда составлен клетчатый квадрат
где
Значит, его площадь не менее
С другой стороны, его площадь не больше, чем суммарная площадь всех
прямоугольников
то есть не больше
Противоречие.
не сможет
Ошибка.
Попробуйте повторить позже
На координатной плоскости нарисована парабола Для данного числа
рассматриваются трапеции, вписанные в эту параболу
(то есть все вершины трапеции лежат на параболе), у которых основания параллельны оси абсцисс, а произведение длин равно
Докажите, что диагонали всех таких трапеций проходят через одну точку.
Источники:
Подсказка 1:
Попробуйте ввести координаты и написать уравнение диагонали AC. Как оно будет выглядеть?
Подсказка 2:
Пусть точки A и C имеют координаты (a, a²) и (c, c²). Тогда уравнение AC примет вид y = (a + c)x − ac. По всей видимости, мы хотим найти точку, значение прямой в которой будет выражаться лишь через k.
Подсказка 3:
Обратите внимание на величину ac, она фиксирована и равна −k²/4.
Пусть — одна из рассматриваемых трапеций,
и
Пусть точки
и
имеют координаты
и
Легко получить уравнение прямой
что после сокращения на превращается в
Но равно произведению половин оснований трапеции. Отсюда
Следовательно, прямая
проходит через
фиксированную точку
![]()
Ошибка.
Попробуйте повторить позже
На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Для игры в настольный теннис навылет всех
жителей острова разделили на две команды и
причём в
жителей было больше, чем в
Начали игру два игрока разных
команд; после каждой партии проигравший игрок навсегда выходил из игры, и его заменял другой (ещё не игравший)
член его команды. Проиграла команда, все члены которой вышли из игры. После турнира каждого члена команды
спросили: «Правда ли, что в какой-то игре ты проиграл лжецу», а каждого члена команды
спросили: «Правда ли,
что ты выиграл хотя бы у двух рыцарей». Все ответы оказались утвердительными. Какая команда победила —
или
?
Источники:
Подсказка 1:
Может ли в команде B быть рыцарь?
Подсказка 2:
Тогда он выиграл у каких-то двух рыцарей из A. Обратите внимание на количество поражений этих рыцарей. Не возникает противоречие с условием?
Подсказка 3:
Значит, в B только лжецы. Может ли A состоять только из рыцарей? Не забывайте, в A больше жителей.
Пусть в есть хотя бы один рыцарь
Тогда
выиграл хотя бы у двоих рыцарей из
пусть
— один из них. Поскольку
—
рыцарь, он правдиво ответил на заданный ему вопрос, то есть он проиграл лжецу. Но из правил следует, что каждый
игрок проигрывает не более одного раза, а
проиграл и рыцарю
и лжецу. Противоречие, значит,
состоит лишь из
лжецов.
Предположим, что состоит только из рыцарей. Тогда каждый из них проиграл какому-то лжецу из
Однако каждый лжец в
выиграл не более чем у одного рыцаря из
так как он солгал. Следовательно, разным рыцарям из
соответствуют разные лжецы из
поэтому в
людей не меньше, чем в
; противоречие.
Таким образом, в команде есть хотя бы один лжец; обозначим одного из них через
Тогда
солгал, то есть он не проиграл ни
одному лжецу из
а значит, ни одному игроку из
Это значит, что
либо выиграл все свои партии, либо до него не дошла очередь. В
любом случае команда
выиграла.
победила
Ошибка.
Попробуйте повторить позже
В ряд выписаны по одному разу все натуральные числа от 1 до 1000 в каком-то порядке. Докажите, что можно выбрать несколько стоящих подряд выписанных чисел, сумма которых больше 100000, но не превосходит 100500.
Источники:
Среди наших чисел где-то есть Покажем для начала, что можно выбрать числа с одной стороны от числа
так, чтобы их сумма
была больше 100000. Сумма всех без чисел без
равна
Тогда по принципу Дирихле с одной из сторон от числа сумма чисел не меньше 250000. Тогда, очевидно, с одной
стороны от числа
можно выбрать несколько подряд идущих чисел так, чтобы их сумма превосходила 100000. Без
ограничения общности будем полагать, что эти числа находятся справа от
(то есть числа, общая сумма которых не
меньше 250000). Обозначим эти числа
…,
где
— первое число справа от
— второе число и так
далее.
Выберем наименьшее такое что
Если теперь
то мы уже нашли подходящие числа. Предположим, что это не так. Тогда — наименьшее такое число, что
поскольку
в силу выбора Покажем, что сумма
подходит.
Во-первых, все слагаемые этой суммы в нашем ряду стоят подряд.
Во-вторых, по условию. Обозначим
Тогда и, следовательно,
Остается доказать, что эта сумма не превосходит Для этого используем знание о том, что
Тогда
Ошибка.
Попробуйте повторить позже
Дан равнобедренный треугольник (
). На продолжениях боковых сторон
и
за точку
отмечены точки
и
соответственно, а на основании
отмечена точка
причем
и
Докажите, что
Источники:
Подсказка 1:
Рассмотрим точку O — середину дуги DBE окружности, описанной около треугольника.
Подсказка 2:
Чем является отрезок OB в треугольнике DBE и в треугольнике ABC?
Подсказка 3:
Обратите внимание на треугольники ACB и EOD. У них довольно много равных элементов.
Подсказка 4:
Они равны. Это значит, что углы ABC и DOE равны. Если бы точка O была центром окружности, описанной около треугольника DFE, то угол DOE был бы центральным, соответствующим вписанному углу DFE.
Первое решение. Обозначим через середину дуги
окружности, описанной около треугольника
Прямая
является
внешней биссектрисой в треугольнике
а следовательно, и в треугольнике
Но треугольник
равнобедренный, поэтому
Заметим далее, что Таким образом, в равнобедренных треугольниках
и
равны углы при
вершинах, а также основания, поэтому равны и сами треугольники. Отсюда, во-первых,
Во-вторых, расстояние от точки до прямой
равно расстоянию от точки
до
а последнее равно расстоянию от
до
(поскольку
). Значит, точка
лежит на биссектрисе угла между прямыми
и
.png)
Из условия вытекает, что эта биссектриса является серединным перпендикуляром к отрезку
Таким образом,
Иными словами, точка
— центр окружности, описанной около треугольника
Следовательно,
что и требовалось.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Для начала сделаем замечание. Пусть на прямой выбраны точки
и
такие, что
и
тогда
и
Действительно, если это не так и, скажем, точки
и
лежит на луче
то
что невозможно.
Построим теперь такие точки. Пусть прямые и
пересекаются в точке
для определённости, пусть
лежит на
луче
Выберем на прямой
точку
такую, что
Тогда
— трапеция с равными углами при
основании; следовательно,
и
Пусть диагонали
и
пересекаются в точке
Пусть,
наконец, описанные окружности треугольников
и
вторично пересекают прямую
в точках
и
соответственно.
Поскольку — биссектриса угла
получаем
и
Кроме того,
Значит, поэтому треугольник
получается из
поворотом вокруг точки
Отсюда нетрудно получить,
что
Далее, из вписанности и симметрии имеем
По замечанию выше получаем, что и
Осталось завершить решение. Имеем Отсюда следует, что точки
и
лежат на одной
окружности. Значит,
что и требовалось доказать.
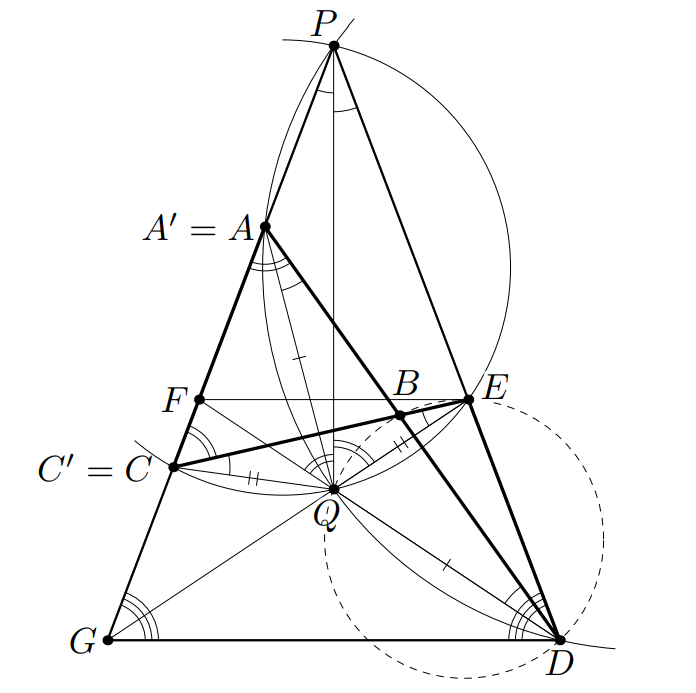
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Если то точка
совпадает с
что невозможно. Поэтому можно считать, что прямые
и
пересекаются. Кроме того, можно показать, что в условиях задачи
всегда лежит именно на луче
______________________________________________________________________________________________________________________________________________________
Третье решение. Как и в предыдущем решении, достроим равнобокую трапецию с точкой пересечения диагоналей
Как мы
видели в том же решении, достаточно доказать, что точки
и
лежат на одной окружности.
Выберем точку так, что четырёхугольник
— параллелограмм. Тогда
— также параллелограмм, ибо
Значит,
и
первое равенство означает, что лежит на серединном перпендикуляре к
а второе — что
это внешняя биссектриса угла
Но, как известно, эта внешняя биссектриса вторично пересекает описанную окружность треугольника
в точке,
лежащей на серединном перпендикуляре к
значит,
и есть эта точка, и точки
лежат на одной
окружности.
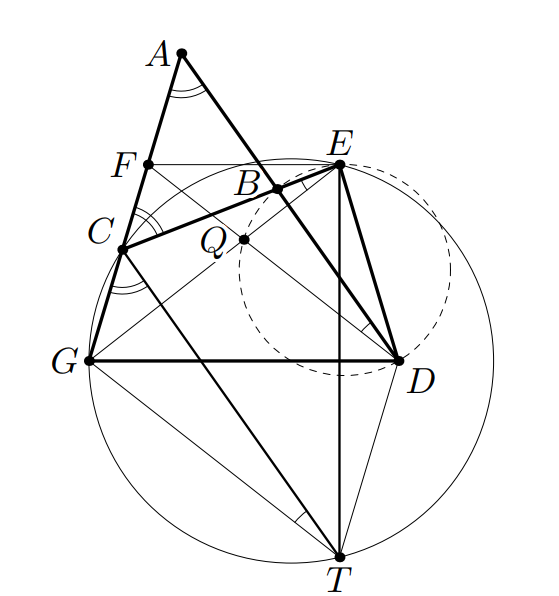
Наконец, из этой окружности и двух параллелограммов получаем
то есть точки
и
лежат на одной окружности; это мы и хотели доказать.
Ошибка.
Попробуйте повторить позже
На доске записано 7 различных чисел, сумма которых равна 10. Петя умножил каждое из них на сумму остальных шести и записал 7 полученных произведений в тетрадь. Оказалось, что в тетради встречаются только четыре различных числа. Найдите одно из чисел, записанных на доске.
Источники:
Подсказка 1:
Давайте заметим, что для числа x на доске, в тетрадь будет записано число x(10 - x) = 10x - x².
Подсказка 2:
Пусть f(x) = 10x - x². Если f(a) = f(b), то как связаны a и b?
Подсказка 3:
Либо a = b, либо a + b = 10. Ясно, что первый вариант в контексте задачи невозможен. Значит, некоторые числа в тетради разбиваются на пары с суммой 10. Учитывая, что в тетради всего 4 различных числа, сколько таких пар?
Для каждого числа написанного на доске, произведение
и суммы шести оставшихся равно
Квадратичная функция принимает все значения, кроме максимального, два раза — а именно, в точках
и
Значит, если
при
то
Таким образом, каждое число встречается в тетради не более двух раз. Значит, так как в тетради всего четыре различных числа,
три из них встречаются по два раза, и ещё одно — один раз. Таким образом, шесть из семи чисел на доске разбиваются
на пары так, что сумма чисел каждой пары равна Значит, сумма этих шести чисел равна
тогда седьмое число
равно
-20
Ошибка.
Попробуйте повторить позже
На окружности длиной 1 метр отмечена точка. Из неё в одну и ту же сторону одновременно побежали два таракана с различными постоянными скоростями. Каждый раз, когда быстрый таракан догонял медленного, медленный мгновенно разворачивался, не меняя скорости. Каждый раз, когда они встречались лицом к лицу, быстрый мгновенно разворачивался, не меняя скорости. На каком расстоянии от отмеченной точки могла произойти их сотая встреча?
Источники:
Подсказка 1:
Попробуйте проанализировать первые несколько встреч.
Подсказка 2:
Вам не кажется, что у этого движения есть некоторая цикличность? Сначала оба бегут вперёд, потом один назад и другой вперёд, потом оба назад, потом один вперёд и один назад, затем оба вперёд. Проанализируйте этот цикл встреч.
Подсказка 3:
Обратите внимание на расстояния, которые проходят тараканы между каждой из встреч в рамках цикла. Нет ли среди них равных?
Подсказка 4:
Покажите, что каждая четвёртая встреча происходит в точке старта.
Первое решение. Назовём быстрого и медленного таракана и
соответственно. Если таракан бежит в том же
направлении, что и в момент старта, то будем говорить, что он бежит вперёд, в противном случае будем говорить, что он бежит
назад.
До первой встречи оба таракана бегут вперёд, между первой и второй встречами бежит вперёд, а
— назад. Между второй и
третьей встречами оба таракана бегут назад, а между третьей и четвёртой встречами
бежит назад, а
— вперёд. Наконец, на
четвёртой встрече
разворачивается, и они оба снова начинают бег вперёд.
Будем следить за перемещением Если между двумя встречами тараканы бегут в противоположные стороны, между такими
встречами всегда проходит одно и то же время, а значит,
всегда пробегает одно и то же расстояние. Таким образом, между первой и
второй встречами, а также между третьей и четвертой встречами
пробегает одно и то же расстояние в противоположных
направлениях. Аналогично, когда между двумя встречами тараканы бегут в одном направлении, это тоже всегда занимает одинаковое
время, и
пробегает одно и то же расстояние. Таким образом, до первой встречи, а также между второй и третьей встречами
также
пробегает одно и то же расстояние в противоположных направлениях. Стало быть, в момент четвертой встречи
(а значит, и
) будет
в точке старта.
Далее эта ситуация будет повторяться каждые встречи. Следовательно, в точке старта тараканы будут и в момент сотой
встречи.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Обозначим тараканов так же, как и выше; пусть их скорости равны м/с. Для определенности будем считать,
что изначально тараканы бегут по часовой стрелке, и расстояние будем отмерять именно в этом направлении.
Когда тараканы бегут в одну сторону, скорость удаления от
равна
, поэтому до первой встречи они будут бежать
секунд, и
до встречи пробежит
метров. Дальше тараканы будут двигаться навстречу друг другу со скоростью сближения
поэтому до второй встречи они будут бежать
секунд, и до этой встречи
сместится от точки старта
на
Дальше оба таракана будут бежать против часовой стрелки в течение секунд, поэтому общее смещение
от точки старта будет
равно
т.е. в итоге он сместится на расстояние против часовой стрелки. Наконец, после этого
развернётся, и они будут бежать в
противоположных направлениях
секунд. Следовательно, их четвёртая встреча произойдёт на расстоянии
от точки старта.
Таким образом, в четвёртый раз они обязательно встречаются в точке старта и после встречи снова побегут по часовой стрелке. Но тогда их сотая встреча также произойдет в точке старта.
на нулевом
Ошибка.
Попробуйте повторить позже
На стороне остроугольного треугольника
выбраны точки
и
так, что
Точки
и
выбраны
соответственно на отрезках
и
так, что
и
Докажите, что точка пересечения медиан треугольника
равноудалена от прямых
и
Источники:
Подсказка 1:
Попробуйте собрать побольше информации о рисунке. Пусть M — середина стороны BC. Обратите внимание, в каком отношении точки P и Q делят MC и MB. Также не забывайте про свойство точки пересечения медиан.
Подсказка 2:
Пусть G — точка пересечения медиан. Мы получили, что GP параллельна AB и GQ параллельна AC. Попробуйте "поперекидывать" углы.
Подсказка 3:
Обратите внимание, что YP — медиана, проведённая к гипотенузе в треугольнике YBQ. То же самое можно сказать про XQ в XPQ. Это даёт больше возможностей для подсчёта углов.
Подсказка 4:
Попробуйте показать, что GP — биссектриса угла YPC, GQ — биссектриса угла XPB. Подумайте, почему это даст требуемое.
Пусть — середина
тогда
— ещё и середина
Пусть
— точка пересечения медиан треугольника
По свойству медианы имеем А так как
получаем, что
Тогда
и
Но
— медиана прямоугольного треугольника
поэтому
Значит,
то
есть
— биссектриса угла
Поэтому точка
равноудалена от прямых
и
.png)
Аналогично, – биссектриса угла
и потому точка
равноудалена от
и
Значит, она равноудалена от трёх
прямых
и
Ошибка.
Попробуйте повторить позже
Правильный треугольник со стороной 111 разбит прямыми, параллельными его сторонам, на правильные треугольники со
стороной 1. Все вершины этих треугольников, кроме центра треугольника
отмечены. Назовём множество из нескольких
отмеченных точек линейным, если все эти точки лежат на одной прямой, параллельной стороне
Сколько существует
способов разбить все отмеченные точки на 111 линейных множеств? (Способы, отличающиеся порядком множеств, считаются
одинаковыми.)
Источники:
Рассмотрим равносторонний треугольник со стороной разобьём его на правильные треугольнички со стороной
и отметим
все вершины этих треугольников; полученную конструкцию назовём
-треугольником. В дальнейшем под прямыми мы
всегда будем понимать прямые, параллельные сторонам этого треугольника и проходящие через хотя бы одну отмеченную
точку.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Пусть — отмеченная точка в
-треугольнике. Тогда существует единственный способ провести
прямых так, что все
отмеченные точки, кроме, возможно,
покрыты этими прямыми. А именно, для каждой стороны
-треугольника надо провести все
прямые, параллельные ей и лежащие между этой стороной и точкой
включая саму сторону, но исключая прямую, содержащую
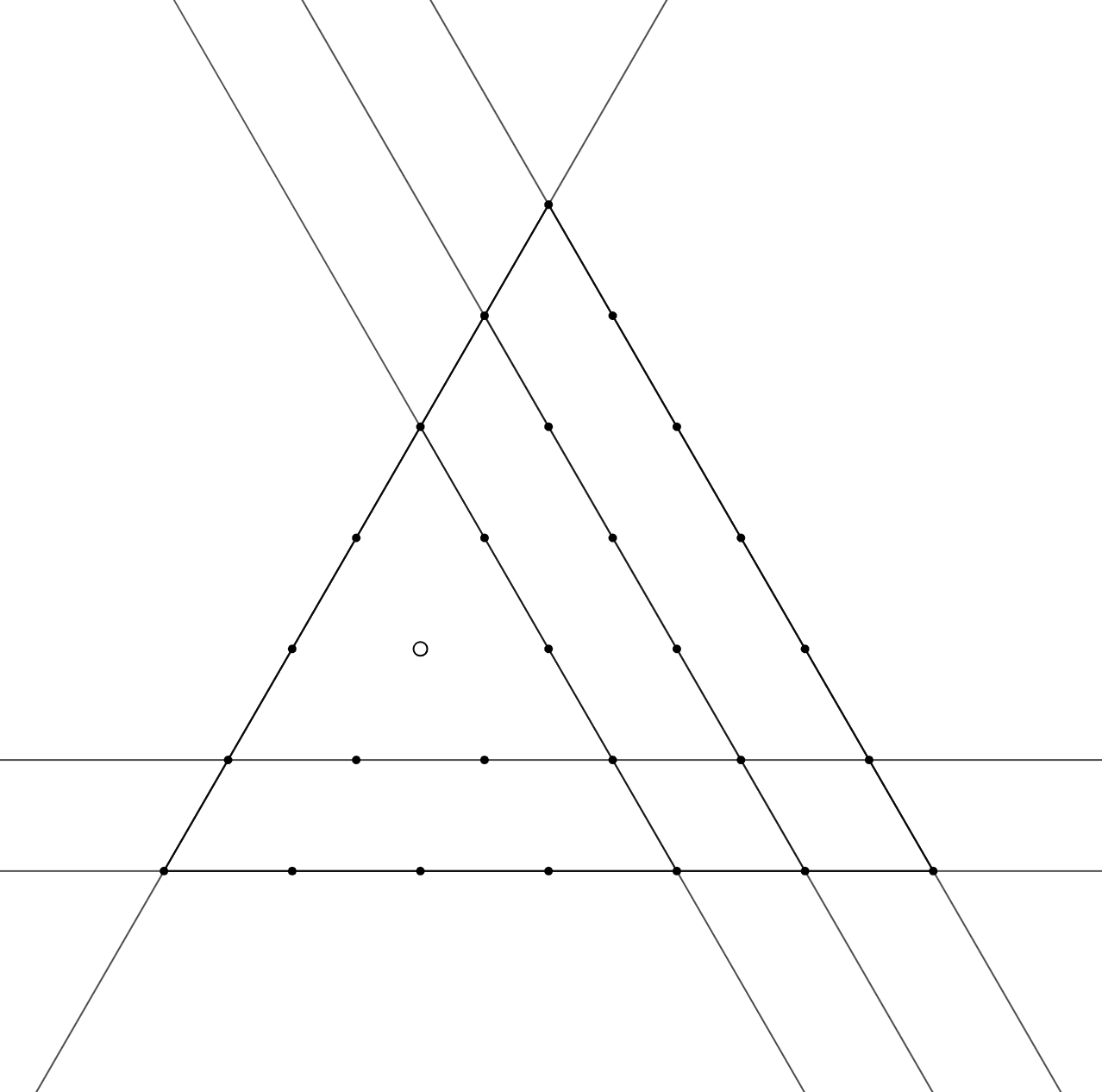
Доказательство. Индукция по База при
проверяется легко: надо провести прямую, содержащую две оставшихся точки,
кроме
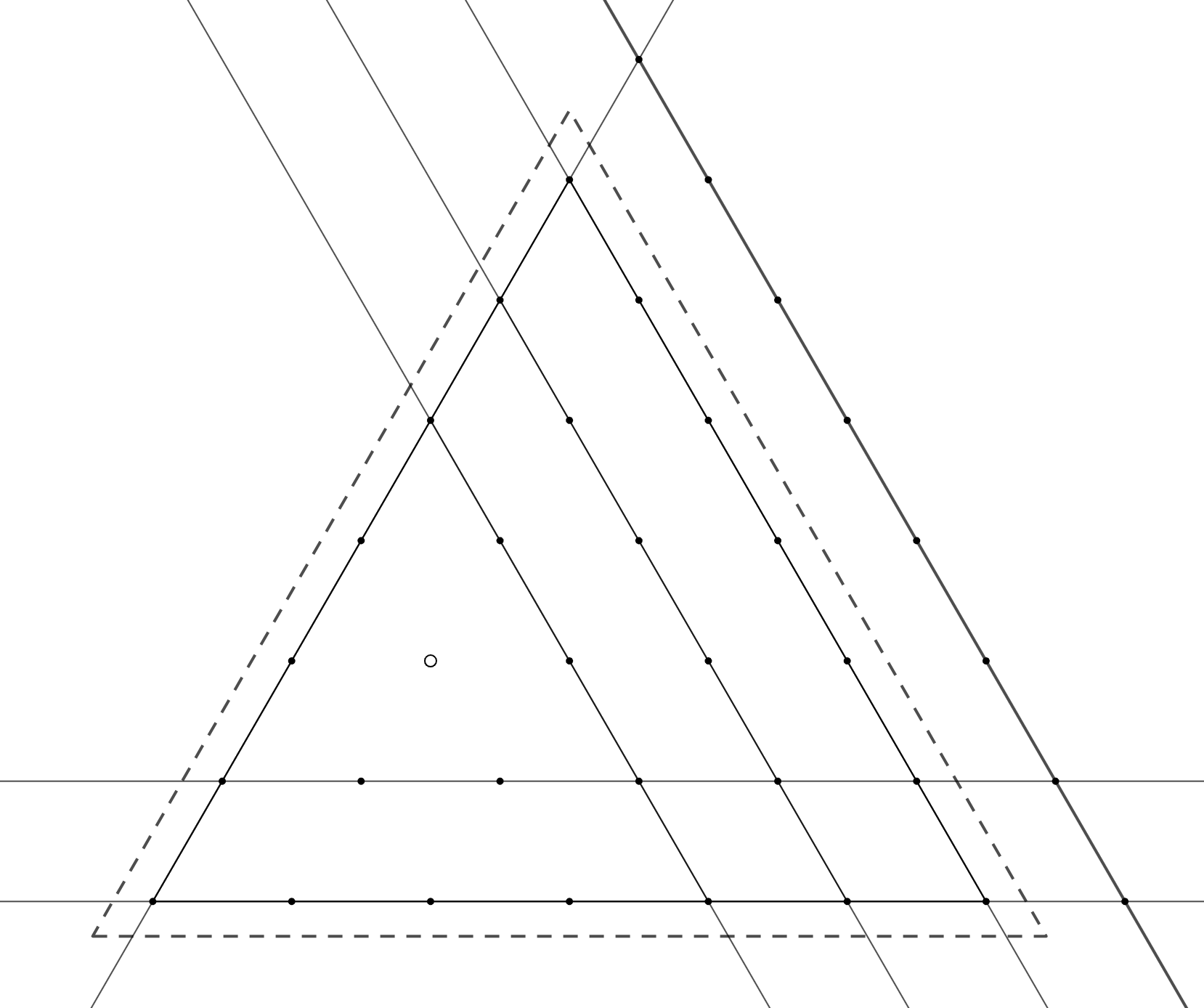
Для перехода рассмотрим сторону -треугольника, на которой не лежит
Если прямая, содержащая эту сторону, не
проведена, то все
отмеченных точек на этой прямой должны быть покрыты различными прямыми; это невозможно,
так как прямых
Значит, эта прямая проведена. Выкинув её и точки
-треугольника, лежащие на ней, получаем
-треугольник, в котором проведено
прямых с теми же условиями. Осталось применять предположение
индукции.
_________________________________________________________________________________________________________________________________________________________________________________
Перейдём к задаче. Рассмотрим одно из разбиений на линейные множества. Для каждого множества проведём прямую, его содержащую.
Тогда эти прямые покрыли все отмеченные точки -треугольника, кроме, возможно, его центра
Значит, эти прямые устроены так, как
описано в лемме, и для любого разбиения этот набор прямых один и тот же.
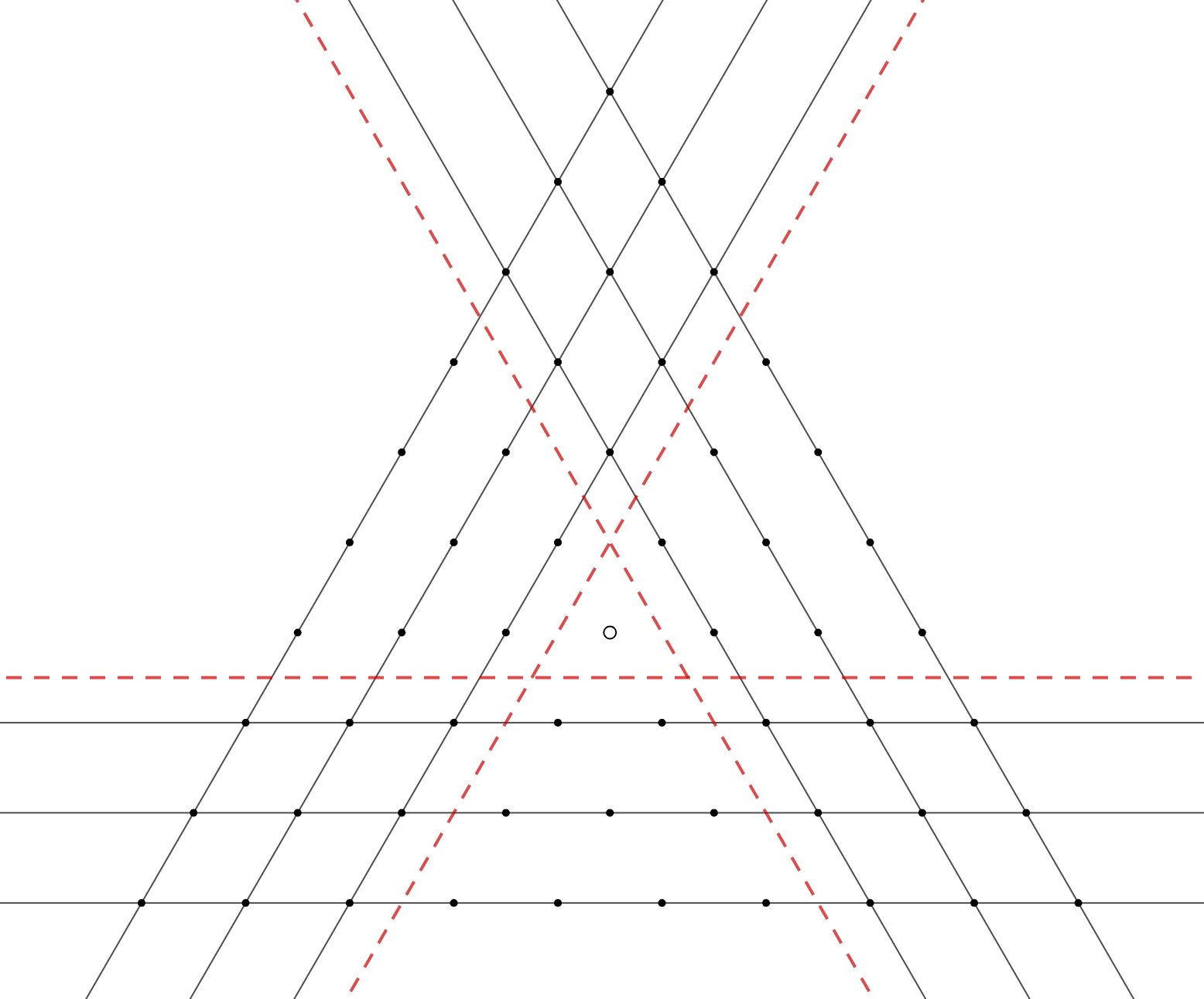
Заметим, что наш -треугольник разбился на
областей: три «ромба» в углах, состоящих из точек, покрытых нашими прямыми
дважды, и три «трапеции» у сторон, в которых каждая точка покрыты одной прямой. Тогда каждая точка в «трапеции» относится к
множеству, лежащему на этой прямой; каждую же точку в «ромбе» можно отнести к любому из двух множеств, лежащих на проходящих
через неё прямых. Все такие выборы можно сделать независимо друг от друга. Поскольку в каждом из трёх «ромбов» всего
точек,
получаем, что требуемых разбиений ровно
Ошибка.
Попробуйте повторить позже
Существует ли натуральное число такое, что десятичные записи чисел
и
отличаются перестановкой цифр?
(Иначе говоря, в десятичных записях чисел
и
должно быть поровну цифр 0, поровну цифр 1, …, поровну цифр
9.)
Источники:
Первое решение. Заметим, что числа и
получаются друг из друга перестановкой цифр.
Пусть теперь
Положим
Заметим тогда, что
Иначе говоря, десятичная запись числа состоит из блоков
и
(дважды), разделённых нулями; у
числа же
эти блоки суть
и
(дважды). Поскольку блоки
и
отличаются перестановкой
цифр, а блоки
и
одинаковы в обоих записях. Также количества разделяющих нулей в обоих случаях одинаковы, получаем, что
число
удовлетворяет требованиям.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Предположим, что нам удалось найти такое число (возможно, с ведущим нулём), что набор цифр в десятичной
записи числа
отличается от набора цифр в десятичной записи числа
выкидыванием цифры
и добавлением цифры
(иначе
говоря, если к числу
приписать единицу, а к
— четвёрку, то полученные числа отличаются перестановкой цифр). Тогда в качестве
числа
можно выбрать
(где
и
больше количества цифр в числе
). Действительно,
имеем
и мы опять видим, что эти числа состоят из блоков и
разделённых нулями, а блоки получаются друг из друга
перестановкой цифр (по условию на
и
и так как
одинаково в обоих случаях).
Осталось найти такое число Если, например, потребовать, чтобы запись числа
получалась из записи числа
циклическим сдвигом и заменой 4 на 1, то такое число нетрудно найти, выписывая его цифры с конца. Подойдет, например,
пара
да
Ошибка.
Попробуйте повторить позже
Для натурального числа обозначим через
наименьшее общее кратное всех чисел
Существует ли такое натуральное
число
что
Источники:
Подсказка 1
Предположим, что это возможно и посмотрим на максимальную степень двойки, которую можно найти среди первых n+1 чисел. А что можно сказать о степени двойки, которую можно найти среди первых n чисел?
Подсказка 2
Верно! Если максимальная степень двойки среди первых n+1 чисел равна k, то среди первых n точно не меньше k/2. Какой вывод можно сделать?
Предположим, что такое существует. Пусть
делится на
но не делится на
Тогда
Значит, среди чисел
есть число
, делящееся на
Но тогда число
делится на
поэтому
делится на
Тогда, поскольку
то
делится на
что неверно.
Нет



